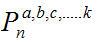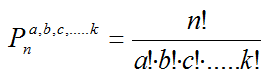6. Permutaciones con repetición
Supongamos
que disponemos de 3 vasos azules iguales, 2 vasos iguales amarillos y 1
naranja. Si quisiéramos ponerlos en línea recta en una estantería. ¿De
cuántas formas distintas lo podríamos hacer?
Para ayudar a contar todos los casos y ayudándonos de que conocemos las
permutaciones sin repetición, vamos a pegar en la parte opuesta, la
que no vemos, etiquetas que identifiquen y distingan como distintos a
todos los vasos. De esta forma disponemos de 6 vasos distintos que se
pueden ordenar de 6! formas distintas.
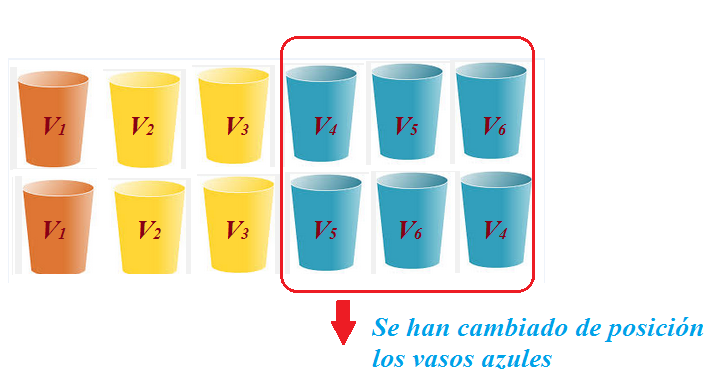
Es decir que si giramos los vasos para que se vean las etiquetas
distinquiríamos todas las permutaciones, pero si no vemos las
etiquetas, ordenaciones que antes eran distintas las veríamos iguales. Las permutaciones anteriores serían identificadas como:
La idea por tanto para contar las permutaciones con repetición es
identificar como una sola agrupación las, en nuestro caso 2! y 3!
reordenaciones que no distinguiríamos. No se distinguirían por tanto (2! x 3! x 1!)
Permutaciones
A continuación puedes observar como se irían confeccionando algunas de
las permutaciones con repetición de 6 elementos de los que uno se repite tres veces, otro dos veces y otro una vez
Denominamos permutaciones con repetición de n elementos en los que uno de ellos se repite "a" veces, otro "b" veces y así hasta el último que se repite "k" veces, donde
(a+b+c+....k = n) a todas las ordenaciones posibles de estos n elementos. Consideramos dos ordenaciones distintas si difieren en el orden de colocación de algún elemento (distinguible).
Denotaremos a este tipo de permutación como
y se calcula como:
En la siguiente escena puedes practicar
con la formación de algunas peermutaciones con repetición. A medida que
practicas irás descubriendo como se van construyendo, sus
características y la idea que permite calcular el número total de
permutaciones con repetición.
En la siguiente escena puedes practicar con ejemplos de formación de algunas permutaciones con repetición.