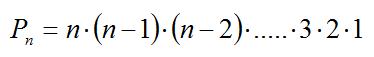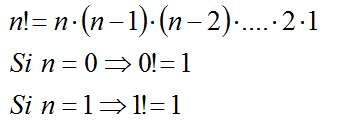4. Permutaciones sin repetición
Imaginemos cuatro
amigos que deciden fotografiarse juntos en una fiesta para conservar el
momento. Si deciden que la fotografía sea de los cuatros en línea. ¿De
cuántas formas
diferentes podrán realizar la fotografía?.
Un primer análisis de la situación nos sitúa el problema al mismo nivel
del que se resolvió en el epígrafe correspondiente a las variaciones
sin repetición. En realidad se trata del mismo razonamiento. La primera
posición la pueden ocupar cualquiera de los cuatro amigos. La segunda
la
pueden ocupar cualquiera menos el que ocupó la primera, es decir tres
posibilidades , y así seguiremos hasta la cuarta posición que podrá
ser ocupada por una persona.
Aplicando ahora el principio general de recuento al
conjunto (B1 x B2 x B3 x B4), el número de posibles agrupaciones sería
4 x 3 x 2 x 1 = 24 resultados distintos.
En la siguiente imagen se presentan algunas de las posibilidades:

Existen muchas situaciones en las que se puede aplicar el mismo razonamiento.
- ¿De cuántas formas diferentes se pueden sentar 5 amigos en una fila de cinco butacas en un cine?
- Un técnico de sonido tiene que unir 10 terminales en 10 conexiones. Si
lo hiciera al azar, ¿ de cuántas formas diferentes podría completar las
conexiones?
- ¿De cuántas formas diferentes se pueden introducir 4 cartas diferentes en 4 sobres distinto?
Vídeo enlazado desde YouTube, licencia de YouTube estándar
Denominamos permutaciones ordinarias o
sin repetición de
n elementos, a cada uno de los distintos grupos que
pueden formarse de manera que:
- En cada grupo entran todos los n elementos.
- Un grupo se diferencia de otro únicamente en el orden de colocación de los elementos.
Al número de permutaciones ordinarias de
n elementos lo representaremos por
Pn y se calcula:
a este número se le denomina
factorial de n y se representa como n! Se utiliza tanto, que aparece
como tecla directa en todas las calculadoras científicas.
En la siguiente escena puedes practicar
con la formación de algunas permutaciones sin repetición. A medida que
practicas irás descubriendo como se van construyendo, sus
características y la idea que permite calcular el número total de
permutaciones sin repetición.