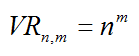4. Variaciones con repetición
Dentro de los juegos de apuestas más populares en España se encuentra
sin duda la quiniela de fútbol. ¿Cuántos resultados posibles pueden
darse en catorce encuentros entre equipos de primera y segunda
división?. Este problema puede resolverse también sin conocimientos
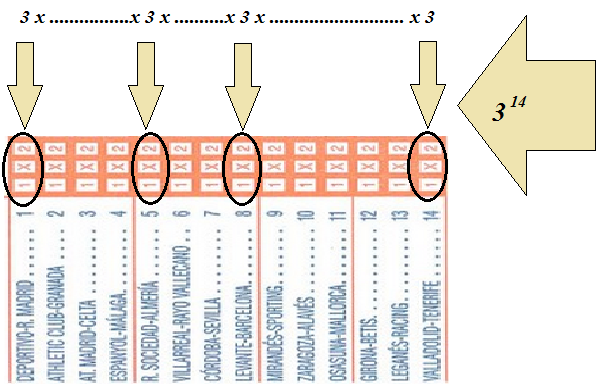
previos de combinatoria. Imaginamos que cada resultado es un grupo de
14 símbolos y que dichos símbolos solamente pueden ser 1, X o 2. Así
para el primer signo que pongamos tendremos 3 posibilidades, para el
segundo también otras 3 y así sucesivamente hasta llegar al símbolo 14.
Ahora no tenemos más que aplicar otra vez el principio general de
recuento al conjunto (P1 x P2 x .......xP14).
Piensa también por ejemplo en:
- Un entrenador de fútbol dispone en la plantilla de su equipo de
7 delanteros de la misma calidad y que pueden actuar indistintamente en
los tres puestos de ataque del equipo. ¿Cuántas delanteras distintas
podría confeccionar?
- ¿De cuántas maneras diferentes se pueden repartir tres premios distintos entre Juan, Pedro, María, Alicia y Pilar?
En combinatoria denominamos variaciones con repetición de
n elementos tomados de
m en
m, (obsérvese que no hay restricción alguna en cuanto a los valores de
n y
m), a los distintos grupos de
m elementos, repetidos o no, que se pueden formar. Considerando:
- En cada grupo hay m elementos repetidos o no.
- Dos agrupaciones son diferentes si difieren en algún elemento o en el orden de colocación.
Al número de variaciones con repetición lo denotaremos,
VRn,m y se calcula:
En la siguiente escena puedes practicar
con la formación de algunas variaciones con repetición. A medida que
practicas irás descubriendo como se van construyendo, sus
características y la idea que permite calcular el número total de
variaciones con repetición.