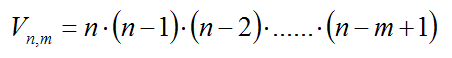3. Variaciones sin repetición
Supongamos que a un concurso literario
en el que se conceden tres premios distintos, se presentan ocho
escritores. Nos
preguntamos por las distintas formas en las que se pueden conceder
estos premios.
Este problema sin duda se puede
resolver sin necesidad de conocimientos previos sobre combinatoria.
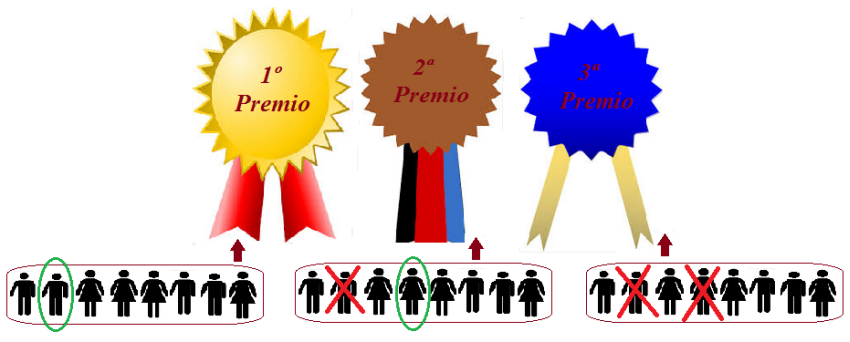
Pensemos que disponemos de tres puestos. Para el primero se puede
elegir a cualquiera de los ocho participantes. Para el segundo, no
puedo elegir al que ya está elegido para el primero, por tanto
solamente podremos elegirlo entre los siete restantes. Para el tercero,
siguiendo el mismo razonamiento nos quedarán seis participantes. Ahora
aplicando el principio general de recuento al conjunto (P1 x P2 x P3), el
total de resultados posibles para el reparto de los tres premio sería: 8 x 7 x 6 = 336.
En combinatoria, denominamos variaciones ordinarias o sin repetición de
n elementos tomados de
m en
m ( siendo
m menor o igual que
n) a cada uno de los distintos grupos de
m elementos escogidos de entre los
n, de manera que:
- En cada grupo, los m elementos sean distintos.
- Dos grupos son distintos, si difieren en algún elemento o en el orden de colocación.
El número de variaciones ordinarias lo representamos
Vn,m y se calcula:
En la siguiente escena puedes practicar
con la formación de algunas variaciones sin repetición. A medida que
practicas irás descubriendo como se van construyendo, sus
características y la idea que permite calcular el número total de
variaciones sin repetición.