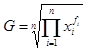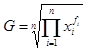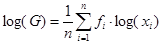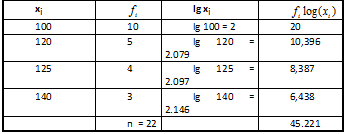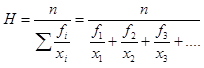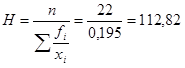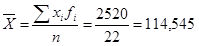Se define la media geométrica como la raíz n-ésima de los productos de todos los valores de la variable o bien como la raíz n-ésima de los productos de los valores xi elevados a sus correspondientes frecuencias absolutas fi. Donde n es el tamaño de la muestra.

Presenta problemas de cálculo cuando los valores de la variable y sus frecuencias conduce a que el radicando sea negativo y coincida que el tamaño de la muestra es par. También en muchas ocasiones, los valores de la distribución nos impiden poder efectuar los cálculos al exceder estos la capacidad de la calculadora. Por ello, en ese caso se suele utilizar los logaritmos:

Y podemos observar que el logaritmo de la media geométrica es la media aritmética de los logaritmos de los valores de la variable.

Suele utilizarse cuando los valores de la variable siguen una progresión geométrica. También para promediar porcentajes, tasas, nº índices, etc., siempre que nos vengan dados en porcentajes.

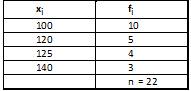
Ejemplo: Hallar la media geométrica de la siguiente distribución:

Para el cálculo es conveniente ampliar la tabla:

De donde tomando antilogaritmos G = anti log(2,0555) = 113,632.

Es la inversa de la media aritmética de las inversas de los valores de la variable, responde a la siguiente expresión:

Se utiliza para promediar velocidades, tiempos, rendimiento, etc. (cuando influyen los valores pequeños).
Su principal inconveniente reside en que cuando algún valor de la variable es 0 o próximo a cero no se puede calcular.

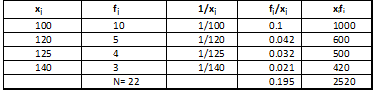
Ejemplo: calcular la media armónica de la siguiente distribución:

Para poder hallarla, es necesario que calculemos el inverso de x y el inverso de la frecuencia por lo que ampliaremos la tabla con 2 columnas adicionales: