EJERCICIOS RESUELTOS

1. Si , el dominio de esta función es el conjunto de todos los números reales tales que . Al despejar el valor de la variable en esta expresión, obtenemos . Por lo tanto, el dominio de la función es .

2. Si , el dominio está dado por todos los números reales tales que . Es decir , por lo tanto y

lo que es equivalente a y .

Entonces, el dominio de la función es: .

3. Si , el dominio lo forman todos los números reales tales que el denominador , pero como esta expresión es un polinomio irreductible (se puede verificar con el discriminante de la ecuación cuadrática) podemos afirmar que el denominador es diferente de cero para todo valor de . Así que el dominio lo forman todos los números reales.

4. Si , entonces su dominio serán todos los números reales tales que

Esta desigualdad se resuelve como ya se explicó en el capítulo anterior.

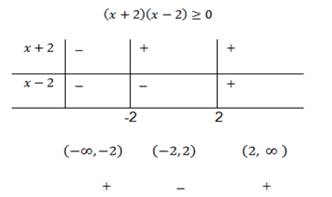
por lo tanto, el dominio de la función es .

Para determinar el rango, es suficiente observar que la función nunca es negativa, por lo tanto el intervalo corresponde al rango de la función.

5. Si , el dominio serán todos los números reales tales que . Pero, como este es un polinomio cuadrático irreductible que siempre es positivo para cualquier valor de la variable, entonces el dominio corresponde al conjunto R.

Para determinar el rango, observemos que la función siempre es negativa, por lo que su rango corresponde al intervalo.

6. Si el dominio lo forman todos los números reales tales que y .

Para determinar el dominio de , resolvamos la desigualdad

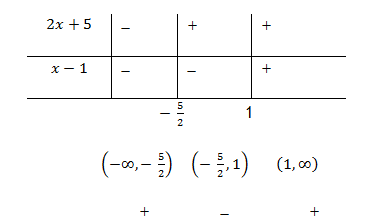
el dominio de la función es

7. La función tiene por dominio todos los números reales.

8. La función tiene por dominio todos los números reales excepto el número -5, es decir .

9. El dominio de la función definida por tramos

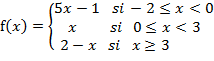es la unión de los intervalos donde está definida, es decir, .

10. Para hallar el dominio de la función 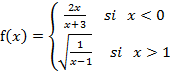es importante observar que el primer tramo está definido para todos los números reales negativos excepto para -3 y el segundo tramo está definido para todos los números reales mayores que 1. Por tanto el dominio de esta función está dado por

11. En la función se debe cumplir que la cantidad sea mayor que cero, o sea

por lo que el dominio es el intervalo .

12. El dominio de la función lo forman todos los números reales tales que , es decir lo que es equivalente a tener

13. El dominio de la función es R.

14. El dominio de la función es , porque en el denominador del exponente se hace cero.