EJERCICIOS
PROPUESTOS
1. Encuentre el dominio y el rango de la
función dada:
a.
![]()
b. ![]()
c.
![]()
d. ![]()
2. Encuentre el dominio de la función dada:
a.
![]()
b. ![]()
c.
![]()
d. ![]()
3. Determine el dominio y trace la gráfica de
la función dada:
a.
![]()
b. ![]()
c.![]()
d. ![]()
e.
![]()
f.
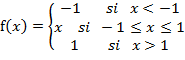
g.
![]()
h.
![]()
i.
![]()
j.
![]()
k.
![]()
l.
![]()
m.
![]()
n.
![]()
o.
![]()
p. 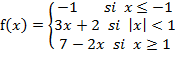
4. En cada uno de los ejercicios siguientes
obtenga una fórmula para la función descrita y determine su dominio:
a. Un rectángulo
tiene 20 m de perímetro. Exprese el área
del rectángulo en función de la longitud de uno de sus lados.
b. El área de un
triángulo equilátero en función de la longitud de uno de los lados.
5. Una caja rectangular abierta con volumen
de 2m3 tiene base cuadrada.
Exprese el área de la superficie de la caja en función de la longitud de
uno de los lados de la base.
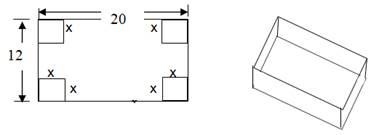
6. Con una hoja rectangular de cartón cuyas
dimensiones son 12 pulgadas por 20 pulgadas, se va a construir una caja abierta
recortando cuadrados iguales de lado x en cada una de las esquinas y luego
doblando los bordes hacia arriba, como se ilustra en la figura. Exprese el
volumen V de la caja en función de x.
7. Una empresa compró maquinaria nueva por
$50.000.000, se deprecia linealmente cada año un 10% de su costo original,
entonces:
a. Exprese el valor
de la maquinaria en función de su antigüedad.
b. Calcule el valor
de la maquinaria después de 4 años.
c. Bosqueje la
gráfica del costo de la maquinaria en función del tiempo.
d. Responda: ¿Cuándo
la maquinaria se deprecia totalmente?
8. La temperatura medida en grados Fahrenheit
(°F) tiene un cambio constante en relación con la temperatura medida en grados
Celsius (°C). Si se sabe que 0°C son equivalentes a 32 °F y 100 °C son
equivalentes a 212 °F:
a. Hallar un modelo matemático que describa
la relación entre °F y °C.
b. Convertir -15°C a °F.
c. Convertir 68°F a °C.
9. Un tanque contiene
a. ¿Cuántos litros de
agua entran al tanque cada hora?
b. Hallar el modelo
matemático que represente la situación.
A partir del modelo
matemático del numeral b. responder lo siguiente:
c. ¿A qué horas hay
en el tanque
d. ¿Cuánta agua habrá
en el tanque a las 11:30 a.m.?
e. ¿Cuándo quedará
lleno el tanque?
10. Entre 1980 y 2008, un coleccionista de
libros raros compra libros para su colección a una tasa constante por año. Si
en 1980 tenía 420 libros en 2000 tenía
1.220 libros. Determinar:
a. Una función que
relacione el número de libros por año.
b. Calcule la
cantidad de libros que tenía el coleccionista en 1993.
c. En qué año tiene
el coleccionista 1.380 libros.
11. Si un tractor cuesta $120.000 y cada año
se devalúa 8% de su precio original:
a. Encuentre una
fórmula para el valor V de la máquina después de t años.
b. Determine el valor
del tractor a los 5 años de realizada la compra.
c. ¿Cuándo se devalúa
totalmente?
12. Una empresa de
alquiler de lavadoras cobra $2.500 por llevar y recoger la máquina, más $1.300
por hora:
a. Escriba la fórmula
del costo total de la renta para t horas.
b. Si usted dispone
de $7.000, por cuánto tiempo puede arrendar la lavadora.
13. La producción de café en el municipio de
Andes creció linealmente durante los años 2000 a 2011. En el año 2002 fue de
200.000 cargas y en 2007 de 370.000:
a. Escriba una
ecuación que represente la producción de café durante el periodo en mención.
b. Indique cuál fue
la producción en los años 2000 y 2011.
14. El ingeniero de una planta de fabricación
de sillas encontró que a la planta le cuesta 22 millones de pesos fabricar 110
sillas en un día y 48 millones de pesos fabricar 300 sillas diariamente.
Exprese el costo de producción ![]() como función del número
como función del número ![]() de sillas producidas (suponga que la relación
es lineal). Indique la pendiente de la función y explique qué significa. ¿Cuál es el intercepto con el eje vertical y
qué significado tiene en el contexto dado?
de sillas producidas (suponga que la relación
es lineal). Indique la pendiente de la función y explique qué significa. ¿Cuál es el intercepto con el eje vertical y
qué significado tiene en el contexto dado?
15. La tasa de inflación anual en México
durante el periodo comprendido entre 2001 a 2009, está dada por la función: ![]() , donde
, donde ![]() representa el número de años desde 2001:
representa el número de años desde 2001:
a. ¿En qué año la
tasa de inflación será mínima?
b. ¿Cuál es la tasa
mínima de inflación?
c. ¿Cuál es la tasa
de inflación en 2005?
16. Durante el festival de cine de Cartagena
la asistencia, en un día cualquiera, a las funciones en cierto teatro, estuvo
representada por el modelo ![]() , donde
, donde ![]() representa el número de personas asistentes al
teatro y t el tiempo trascurrido (en horas), a partir de las 11:00 a.m., hora
en que abrió el teatro. De acuerdo a esta información, determinar:
representa el número de personas asistentes al
teatro y t el tiempo trascurrido (en horas), a partir de las 11:00 a.m., hora
en que abrió el teatro. De acuerdo a esta información, determinar:
a. ¿Cuántas personas
había en el teatro a las 11:00 a.m.?
b. ¿Cuál fue la asistencia
máxima al teatro en ese día?
c. ¿A qué hora se
presentó la máxima asistencia?
17. La efectividad de un comercial de
televisión depende de cuántas veces lo vea un televidente. Después de algunos
experimentos, una agencia de publicidad encuentra que si la efectividad E se
mide en una escala de uno a diez, entonces ![]() ,
donde n es el número de veces que un televidente ve un determinado comercial.
Para que un comercial tenga efectividad máxima, ¿cuántas veces lo debe ver un
televidente?
,
donde n es el número de veces que un televidente ve un determinado comercial.
Para que un comercial tenga efectividad máxima, ¿cuántas veces lo debe ver un
televidente?
18. Juan tiene una venta de obleas en el
Parque de Bolívar, realizando un estudio
sobre el comportamiento de sus ganancias con la cantidad de obleas vendidas, se
dio cuenta de que sus ganancias seguían el siguiente modelo: ![]()
Donde ![]() representa el número de obleas vendidas y
representa el número de obleas vendidas y ![]() las ganancias, de acuerdo con la información
indique:
las ganancias, de acuerdo con la información
indique:
a. ¿Cuál es la
ganancia máxima que Juan puede obtener?
b. ¿Cuántas obleas
debe vender para tener la ganancia máxima?
c. ¿Cuántas obleas
debe vender para librar la inversión y no tener pérdidas?
19. Simón vende confites en la universidad,
realizando un estudio sobre el comportamiento de sus ganancias, se dio cuenta
de que sus ganancias seguían el siguiente modelo:
![]()
Donde ![]() representa la cantidad de confites vendidos y
representa la cantidad de confites vendidos y ![]() las ganancias, de acuerdo con la información
indique:
las ganancias, de acuerdo con la información
indique:
a. ¿Cuál es la
ganancia máxima que Simón puede obtener?
b. ¿Cuántos confites
debe vender para tener la ganancia máxima?
c. ¿Cuántos confites
debe vender para librar la inversión y no tener pérdidas?
20. Un modelo para determinar el número ![]() de personas de un lugar que han escuchado
cierto rumor t días después es
de personas de un lugar que han escuchado
cierto rumor t días después es ![]() ,
si a los 3 días el rumor lo conocen 150 personas, determinar
,
si a los 3 días el rumor lo conocen 150 personas, determinar
a. ¿Cuántas personas
han escuchado el rumor 10 días después?
b. ¿Cuál es el tiempo
necesario para que el rumor lo conozcan 15.000 personas?
c. ¿Cuántas personas
comenzaron el rumor?
d. Si en el lugar hay
27.000 personas, ¿Cuándo conocieron todas las personas el rumor?
21. Un lago contiene cierta especie de pez.
La población de peces t años después de colocarlos en el lago se modela
mediante la función ![]() ,
3 años después se contaron 20 peces. Determinar
,
3 años después se contaron 20 peces. Determinar
a. ¿Cuántos peces hay
en el lago 8 años después?
b. ¿Cuántos peces hay
en el lago 7 años después?
c. ¿Cuántos peces hay
en el lago 6 años después?
d. ¿Cuándo se
estabiliza el número de peces en el lago? y ¿cuál es ese número de peces?
22. El número ![]() de bacterias en un cultivo crece de tal forma
que matemáticamente su modelo es:
de bacterias en un cultivo crece de tal forma
que matemáticamente su modelo es: ![]() . Determine el número de
bacterias depositadas inicialmente, justo antes de que comenzaran a
reproducirse. ¿Cuántas horas deberán transcurrir para que el número de
bacterias sea de 1.500?
. Determine el número de
bacterias depositadas inicialmente, justo antes de que comenzaran a
reproducirse. ¿Cuántas horas deberán transcurrir para que el número de
bacterias sea de 1.500?
23. Se puede demostrar que la velocidad V de
descenso de un paracaidista en un tiempo t después del lanzamiento se puede
calcular como: ![]() donde t está dado en segundos y la velocidad
en pies/seg., entonces:
donde t está dado en segundos y la velocidad
en pies/seg., entonces:
a. A los 10 segundos
del lanzamiento ¿qué velocidad lleva el paracaidista?
b. ¿En qué
momento tiene una velocidad aproximada
de 26.37 pies/seg?
24. Con los datos del censo de Colombia del
siglo XX, la población de Bogotá puede modelarse mediante: ![]()
donde
![]() es la población en millones y t es el número
de años desde 1800. Con base es este modelo:
es la población en millones y t es el número
de años desde 1800. Con base es este modelo:
a. ¿Cuál será la
población en 2018?
b. ¿En qué año la
población es de 15 millones?
25. A medida que un obrero adquiere más
experiencia en su trabajo, la producción diaria aumenta hasta alcanzar una
máxima. Supóngase que el n-ésimo día de trabajo, el
número ![]() de artículos producidos se calcula mediante el
modelo
de artículos producidos se calcula mediante el
modelo ![]() :
:
a. ¿Cuál es el número
de artículos producidos el día quinto?
b. ¿A los cuántos
días produce el obrero 22 artículos?
26. En un laboratorio de biotecnología se
tiene un cultivo de bacterias en un fermentador durante 4 horas. La población
de bacterias crece rápidamente con el paso del tiempo. La función que relaciona
la cantidad de bacterias y el tiempo t transcurrido en horas es ![]() :
:
a. Determine en
cuánto se incrementa la población en 3 horas.
b. ¿Cuándo habrá una
población de 1.000 bacterias?
27. Utilizar la gráfica de ![]() para realizar la gráfica mediante
transformaciones de funciones, de
para realizar la gráfica mediante
transformaciones de funciones, de ![]() en
el mismo plano.
en
el mismo plano.
28. Utilizar la gráfica de ![]() para realizar la gráfica de
para realizar la gráfica de ![]() ,
mediante transformaciones de funciones, en el mismo plano.
,
mediante transformaciones de funciones, en el mismo plano.
29. Utilizar la gráfica de ![]() y las transformaciones de funciones para
realizar el gráfico de
y las transformaciones de funciones para
realizar el gráfico de ![]() .
.
30. Utilizar la gráfica de ![]() ,
para realizar la gráfica de
,
para realizar la gráfica de ![]() ,
mediante transformaciones de funciones, en el mismo plano.
,
mediante transformaciones de funciones, en el mismo plano.
31. Explique los tipos de transformaciones
que deben realizarse a partir de la función ![]() para obtener la función
para obtener la función ![]() .
Bosqueje esta última.
.
Bosqueje esta última.
32. Utilizar la gráfica de ![]() ,
para realizar la gráfica de
,
para realizar la gráfica de ![]() mediante
transformaciones de funciones, en el mismo plano.
mediante
transformaciones de funciones, en el mismo plano.
33. Utilizar la gráfica de ![]() ,
para realizar la gráfica de
,
para realizar la gráfica de ![]() ,
mediante transformaciones de funciones, en el mismo plano.
,
mediante transformaciones de funciones, en el mismo plano.
34. Utilizar la gráfica de ![]() ,
para realizar la gráfica de
,
para realizar la gráfica de ![]() mediante transformaciones de funciones, en el mismo plano.
mediante transformaciones de funciones, en el mismo plano.
35. Utilizar la gráfica de ![]() ,
para realizar la gráfica de
,
para realizar la gráfica de ![]() mediante transformaciones de funciones, en el
mismo plano.
mediante transformaciones de funciones, en el
mismo plano.
36. Utilizar la gráfica de ![]() ,
para graficar
,
para graficar ![]() mediante transformaciones de funciones, en el
mismo plano.
mediante transformaciones de funciones, en el
mismo plano.