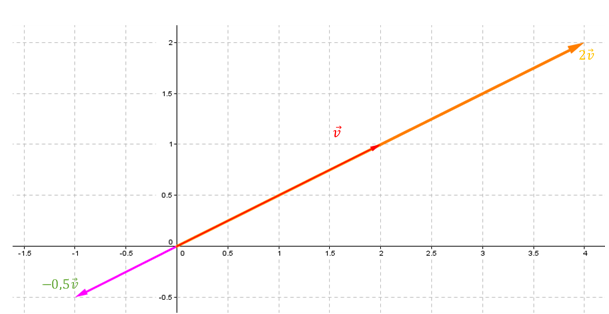
Las combinaciones lineales del vector \(\left( {2,1} \right)\) son todos los vectores de la forma \(\left( {2k,k} \right)\) con \(k \in \mathbb{R}\).

Geométricamente el subespacio generado por \(\left( {2,1} \right)\) es la recta que pasa por el origen y tiene la dirección de dicho vector.
Las combinaciones lineales de los vectores \(\left( {1,0,2} \right),\left( {0,0,1} \right)\) son los vectores coplanares con \(\left( {1,0,2} \right)\) y \(\left( {0,0,1} \right)\):
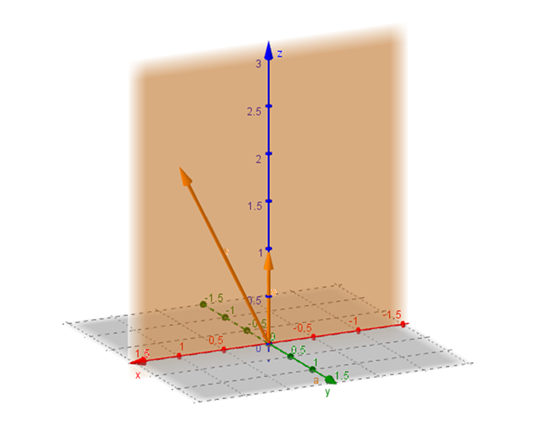
Veamos, analíticamente, cual es el espacio generado por \(\left( {1,0,2} \right),\left( {0,0,1} \right)\):
\[\left( {x,y,z} \right) = \alpha \left( {1,02} \right) + \beta \left( {0,0,1} \right) = \left( {\alpha ,0,2\alpha + \beta } \right)\;\;\;\;\;\;\;\alpha ,\beta \in \mathbb{R}\]
Son todos los vectores con segunda componente nula. Es decir que el subespacio generado es el plano \(y = 0\).
O sea: \(gen\left\{ {\;\left( {1,0,2} \right),\;\left( {0,0,1} \right)} \right\} = \left\{ {\;\left( {x,y,z} \right) \in {\mathbb{R}^3}\;:\;\;y = 0\;} \right\}\)
Tomemos los vectores del ejemplo anterior: \(\left( {1,0,2} \right),\;\;\left( {0,0,1} \right)\) y además el vector\(\;\left( { - 1,0,1} \right)\).
¿Qué espacio generan?
\[\left( {x,y,z} \right) = \alpha \left( {1,02} \right) + \beta \left( {0,0,1} \right) + \gamma \left( { - 1,0,1} \right) = \left( {\alpha - \gamma \;,\;0\;,\;2\alpha + \beta + \gamma } \right)\]
Son vectores con segunda componente nula. Se genera el mismo subespacio que en el ejemplo anterior. Esto se explica porque el tercer vector es coplanar con los primeros dos.