Libros
Interactivos
de Aprendizaje
Encuentro de Geometría y sus Aplicaciones
LIBROS
INTERACTIVOS
DE APRENDIZAJE
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Fondo Editorial Pascual Bravo
Medellín
Título de la obra
Libros interactivos de aprendizaje
Juan Guillermo Rivera Berrío
Otros autores: José Román Galo Sánchez, Mª José García Cebrian, Elena Esperanza Álvarez Sáiz, Josep Mª Navarro Canut, Héctor Aníbal Tabares Ospina, José Gregorio Doria Andrade, Joel Espinosa Longi y Alejandro Radillo Díaz
2019
Diseño del libro: Juan Guillermo Rivera Berrío
Diseño de cubierta: Margarita Patiño Jaramillo
Imagen en la portada: https://www.kisspng.com
Librería turn.js: Emmanuel García
Herramienta de edición: DescartesJS
Fuente: Amaranth
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
El contenido de este libro es bajo liencia (CC BY 4.0) Creative Commons Attribution 4.0 International.
Tabla de contenido
3. Geometría analítica del plano27
4. Geometría analítica del espacio33
6. Curvas y superficies paramétricas45
iii
Prefacio
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red. Algunos de los objetos interactivos se han diseñado con el Editor DescartesJS.
El contenido del libro se ha utilizado para presentar una conferencia en el marco del
24 Encuentro de Geometría y sus Aplicaciones
5
Libro III
Euclides

Los Elementos de Euclides (en griego: Στοιχεῖα, /stoicheia/) y conocido como geometría euclidiana; en griego: Ευκλειδης Γεωμετρια) es un tratado matemático y geométrico que se compone de trece libros, escrito por el matemático y geómetra griego Euclides cerca del 300 a. C. en Alejandría
He aquí la proposición 31 del libro III:
Fuente: https://mathcs.clarku.edu/
9
Oliver Byrne empleó un esquema de colores para la edición de 1847, facilitando el aprendizaje. El resultado se ha descrito como uno de los libros más excepcionales y bellos del siglo XIX.
He aquí la proposición 31 del libro III:
Fuente: https://euclid.ucc.ie/
10
En 2019, quien les expone, presenta el modelo de Byrne con una importante modificación o, mejor, una mejora para el aprendizaje.
He aquí la proposición 31 del libro III:
11
¿Libros interactivos?
¿De aprendizaje?
OVA vs OIA

Encuentro de Geometría y sus Aplicaciones
Algunas definiciones
Objeto de Aprendizaje - OA
El Comité de Estándares de Tecnologías de Aprendizaje (LTSC: Learning Technology Standards Committee) propone la siguiente definición: "Un Objeto de Aprendizaje es cualquier entidad, digital o no digital, la cual puede ser usada, re-usada o referenciada durante el aprendizaje apoyado por tecnología […] Ejemplos de Objetos de Aprendizaje incluyen una lección, un simple archivo JPEG, contenidos multimedia, un video, simulaciones, cuadros digitales, animaciones…"
17
Objetos Virtuales de Aprendizaje - OVA
Los OVA son desarrollados con distintos programas, que tenga formatos técnicos compatibles. Ya que, el propósito es, que puedan ser reutilizados, adaptados, editados, combinados y distribuidos en distintos ambientes de aprendizaje, para que puedan ser usados por todos, sin la limitante del dispositivo electrónico o la modalidad de estudio (https://www.evirtualplus.com/).
Es un recurso digital que puede ser reutilizado en diferentes contextos educativos. Pueden ser cursos, cuadros, fotografías, películas, vídeos y documentos que posean claros objetivos educacionales, entre otros. El concurso de Objetos Virtuales busca contribuir al desarrollo de esquemas virtuales de aprendizaje premiando la creatividad e ingenio de la comunidad educativa nacional (MEN).
18
Objetos Interactivos de Aprendizaje - OIA
Son objetos de conocimiento que permiten a los usuarios del objeto realizar inferencias. Son dos las condiciones que el objeto tiene que satisfacer para ser interactivo: la primera condición consiste en que el objeto es utilizado por alguien para representar algo (un volumen de revolución, por ejemplo) y la segunda, que Contessa (2007) llama razonamiento subrogatorio, es que el objeto permita que sus usuarios realicen inferencias específicas desde el objeto al fenómeno que representa.
19
Por tanto el objeto no sólo integra la teoría que pretendemos representar, también permite intervenir en su percepción en tanto que interactúa en los procesos cognitivos de los usuarios. Este objeto de aprendizaje, así comprendido, se constituye en un efectivo mediador (virtual) entre lo que se representa y el usuario que interpreta, o entre la teoría y el usuario, con dos posibles propósitos: que el usuario intervenga sobre lo representado (he ahí la interactividad) y que infiera y deduzca la teoría que sustenta (he ahí la efectividad); es decir, promueve su conocimiento significativo.
Recursos Educativos Digitales Abiertos - REDA
Todo tipo de entidad digital que tiene una intencionalidad y finalidad enmarcada en una acción educativa cuya información se dispone en una infraestructura de red pública como Internet, bajo un licenciamiento de acceso abierto que permite y promueve su uso, adaptación, modificación y/o personalización.
Ministerio de Educación Nacional. Recursos Educativos Digitales Abiertos - Colombia. Bogotá D.C. : Graficando Servicios Integrados, 2012, pág. 99.
20
Objetos Digitales Educativos - ODE
Un Objeto Digital Educativo (ODE), Material Educativo Digital (MED) u Objeto Didáctico Digital (ODD) es un contenido educativo digital cuya finalidad última es el aprendizaje del usuario y que, en sí mismo, constituye o puede llegar a constituir, mediante su integración con otros objetos más simples, un material educativo multimedia.
21
Un OVA
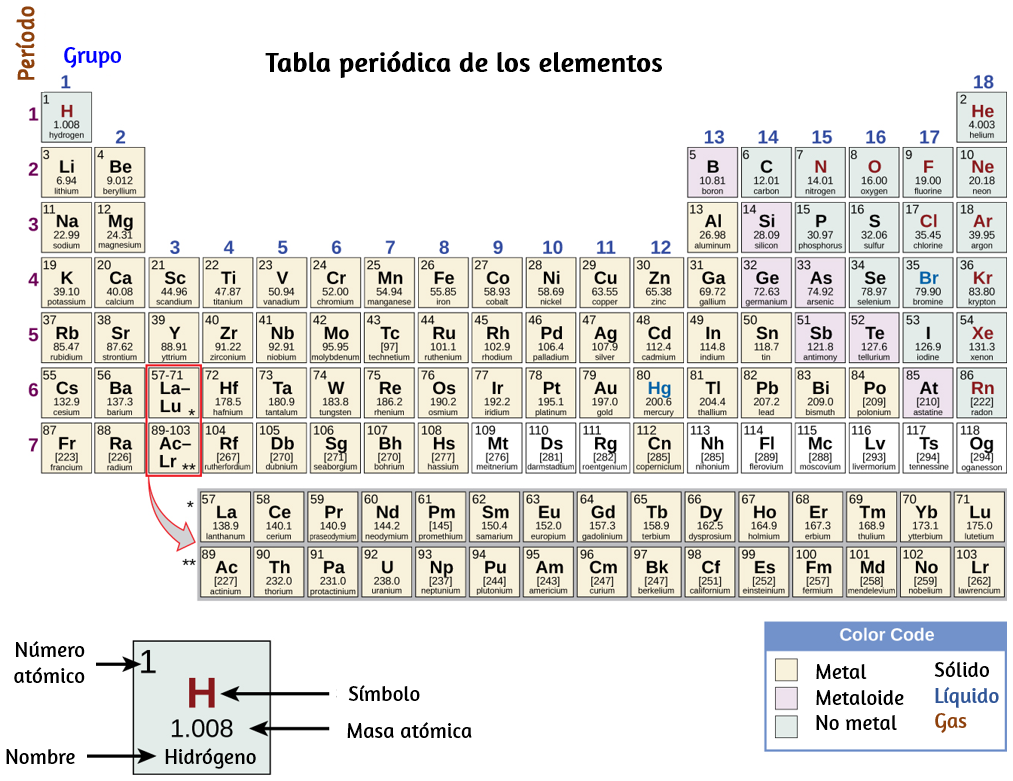
Figura 1.22. La tabla periódica muestra cómo se pueden agrupar los elementos de acuerdo con ciertas propiedades similares. Observa que el color de fondo indica si un elemento es un metal, metaloide o no metal, mientras que el color del símbolo del elemento indica si es un sólido, líquido o gas.
22
Un OIA
Pasa el puntero del ratón sobre un elemento para leer algunas de sus características. También puedes identificar los tipos de elementos metales y no metales. El color del elemento define si se trata de un elemento sólido, líquidos, gaseoso o desconocido.
23
Unidad didáctica
Dewey (1931) destacó el valor instumental del conocimiento como forma de resolver problemas de la vida cotidiana. Este pensamiento tuvo repercusión en autores como Kilpatrick (1981), el cual desarrolló un sistema de proyectos; Morrison (1926) quien extendió sus unidades de trabajo; Bruner (1974) quién creó la educación funcional. Todos ellos presentan estilos peculiares pero tienen en común su preocupación por abordar las tareas de enseñanza-aprendizaje en forma de unidades integradoras del saber (https://www.feandalucia.ccoo.es).
Ejemplo de Unidad Didáctica presentada en https://didactalia.net
24
Geometría analítica
del plano

INTERACTIVO
Operaciones con vectores
28
Bases y coordenadas
29
Ejercicios para practicar
A continuación se presentan más ejercicios para practicar. Puedes elegir en el menú el tipo que prefieras para empezar. De todos ellos se ofrece la solución.
30
Geometría analítica
del espacio

INTERACTIVO
1.3. Operaciones. Combinación lineal
34
35
1.4. Dependencia e independencia lineal. Base
Un conjunto de vectores se dice linealmente dependiente si alguno de ellos se puede poner como combinación lineal de los demás. Cuando no es posible, el conjunto de vectores se dice que es linealmente independiente.
Cuando un conjunto de vectores es linealmente independiente y, además, cualquier vector en el espacio se puede poner como combinación lineal de ellos se dice que forman una base.
36
En IR3 tres vectores linealmente independientes forman una base. Por ejemplo, el conjunto de vectores { i , j , k } con i = (1,0,0), j = (0,1,0), k = (0,0,1) forman una base, recibe el nombre de base canónica.
37
MÉTODOS
NUMÉRICOS

INTERACTIVO
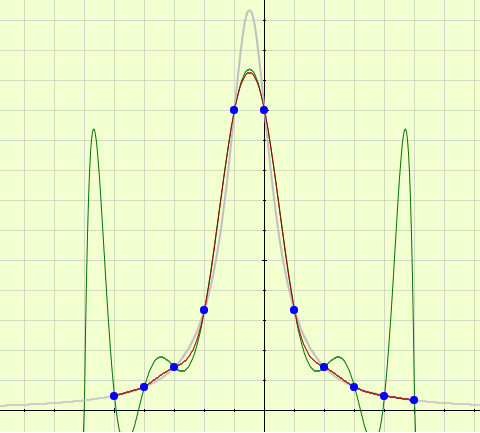
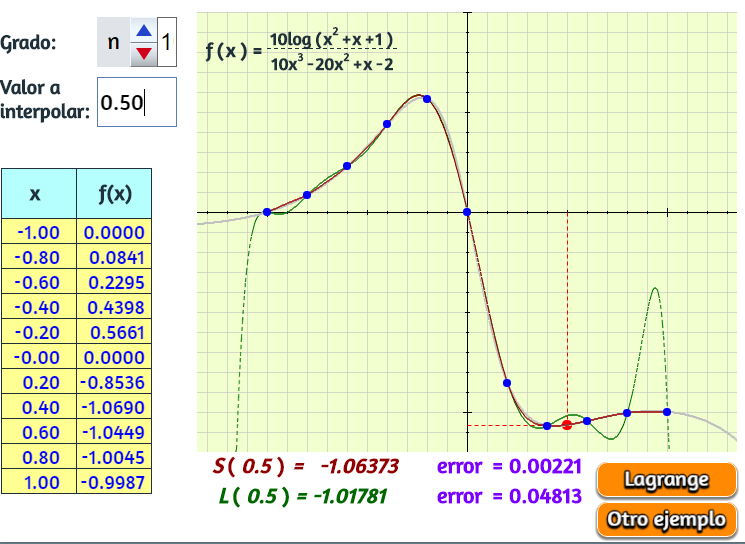
Imagen del primer ejemplo. Observa las oscilaciones de Lagrange (color verde) en los puntos extremos (haz clic sobre la imagen).
Imagen del cuarto ejemplo. Grandes oscilaciones de Lagrange (color verde) en los últimos nodos (haz clic sobre la imagen).
40
Splines cúbicos en Descartes
41
Splines cúbicos en GeoGebra
GeoGebra ofrece un comando para calcular una función splin, dada una nube de puntos; sin embargo, no se sabe qué tipo de trazador o qué método es el que se usa para construirlo, sólo se tiene la siguiente información: "Crea una spline que pase por todos los puntos". Hemos creado una escena con los 10 puntos del primer ejemplo de la escena anterior y usado el comando spline[{A,B,C,D,E,F,G,H,I,L}]. Observa el resultado y concluye (puedes mover los puntos).
42
Splines cúbicos en wxMaxima
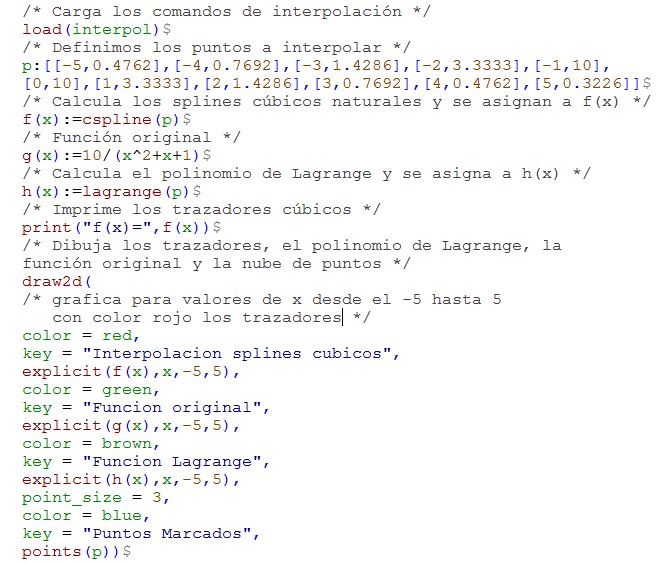
wxMaxima ofrece un paquete de comandos de interpolación, el cual se carga con la instrucción load(interpol). Podemos calcular los splines cúbicos con el comando spline(p), donde p es la matriz donde se almacenan los puntos. En la siguiente imagen observarás las instrucciones para este cálculo (haz clic en la imagen para agrandarla).
43
44
Curvas y
superficies
paramétricas
INTERACTIVO
Figuras de Lissajous
Las figuras de Lissajous fueron descubiertas por el físico francés Jules Antoine Lissajous, quien empleó sonidos de diferentes frecuencias para hacer vibrar un espejo. La luz reflejada en el espejo trazaba una curva cuya forma dependía de la frecuencia del sonido. Estas figuras, entonces, se obtienen de la superposición de dos movimientos armónicos perpendiculares (http://www.euclides.dia.uned.es).
46
En la anterior escena interactiva, diseñada en GeoGebra por Julio Mulero, puedes apreciar la gran diversidad de figuras de Lissajous que puedes obtener.
Ecuaciones paramétricas
En la siguiente escena interactiva, diseñada por José Luis Abreu, puedes observar las ecuaciones paramétricas que definen las figuras de Lissajous. Cambia los valores de los parámetros m y n y trata de obtener las figuras mostradas en la escena de Mulero.
47
Otras caracolas
Como lo habíamos dicho antes, existen varios modelos, de los cuales presentamos dos. El primero corresponde a las siguientes ecuaciones paramétricas:
x = 1.2v(sen2(u)sen(v))
y = 1.2v(sen2(u)cos(v))
z = 1.2vsen(u)cos(u)
48
Una segunda caracola la obtenemos con estas ecuaciones:
x = 2(1 - eu/6π)cos(u)cos2(v/2)
y = = 2(1 - eu/6π)sen(u)cos2(v/2)
z = 1 - eu/3π - sen(v) + eu/6πsen(v)
49
50
DescartesJS
Nivel II
INTERACTIVO
Si observas el archivo interface.html, notarás que sólo usamos dos bloques (evalua y puntos), los cuales ya hemos explicado anteriormente. Su función es comunicar información sobre los elementos gráficos (puntos y rectas) creados en el entorno gráfico, además de atributos como el color.
Finalmente, el esfuerzo en DescartesJS se centra en el selector "Gráficos", desde el cual se muestran mensajes al usuario para que, paso a paso, realice la construcción del objeto geométrico.
52
Una segunda estrategia es haber usado un espacio transparente R2, tipo mascara, que cubre la ventana gráfica de GeoGebra, diseñado de tal forma que los ejes y escala coincidan. Este espacio sólo aparece mientras se marcan los puntos.
Por otra parte, el archivo interface usa tres bloques, dos de ellos ya explicados (puntos y aux). El tercer bloque es "reset", que se ejecuta para reiniciar la escena, su funcionamiento es sencillo, pues sólo ejecuta el comando: document.ggbApplet.reset(), es decir, reinicio. A continuación, presentamos la escena:
53
6.1 Introducción
En el nivel I diseñamos escenas de vídeos interactivos, las cuales usaban las funciones intrínsecas de DescartesJS. En este capítulo emplearemos otras funciones que son propias del vídeo, sea este en local (etiqueta <video>) o reproducido en YouTube; por ejemplo, control de volumen, control de tiempo, (avance o retroceso), autoreproducción (autoplay), entre otros.
Es importante recordar que el objetivo del vídeo interactivo es permitir al usuario interactuar con la escena, en la cual el objeto principal es el vídeo. La interacción se realiza a través de preguntas o de la selección de opciones presentadas como botones o puntos gráficos dibujados sobre el vídeo. Esta interacción se logra si sólo se habilitan los controles de vídeo antes mecionados, que sólo permitan al usuario interferir en la reproducción de acuerdo a una intencionalidad didáctica. La comunicación bidireccional escena – HTML posibilita una gran variedad de alternativas o modelos de vídeos interactivos.
En este capítulo presentamos algunas de estas alternativas. Se hará una descripción técnica de los comandos JavaScript relacionados con la reproducción del vídeo y, por otra parte, se explicará cómo modificar la escena para incorporar otros vídeos y las interacciones correspondientes.
Presentamos, por una parte, modelos que incorporan vídeos almacenados en una carpeta de cada modelo; es decir, modelos para ejecución en local. Si bien es posible reproducirlos en línea en ordenadores y algunos dispositivos móviles, su propósito principal es poderlos descargar e instalar en ordenadores que presentan baja conectividad; por otra parte, presentamos modelos que incluyen enlaces a vídeos de YouTube que, obviamente, requieren conexión a Internet, si bien es posible usar cualquier vídeo entre la gran abundancia que presenta este popular repositorio,
54
2.2.7 Demostrando el teorema de Pitágoras
Este ejemplo corresponde a un vídeo de 3 minutos y 46 segundos, en el que se hacen cuatro preguntas de respuesta escrita. Al final aparece la escena de GeoGebra construida en el vídeo. En este caso la comunicación es sólo entre DescartesJS y el vídeo, puesto que la escena de GeoGebra es simplemente un HTMLIframe embebido en
55
56
FÍSICA
VOLUMEN II
INTERACTIVO
Explicación
Este es el índice de refracción para el agua, y Snell pudo haberlo determinado al medir los ángulos y realizar este cálculo. Entonces habría encontrado que 1.33 era el índice apropiado de refracción para el agua en todas las demás situaciones, como cuando un rayo pasa del agua al vidrio. Hoy, podemos verificar que el índice de refracción esté relacionado con la velocidad de la luz en un medio midiendo esa velocidad directamente.
En la escena interactiva que presentamos en la página siguiente, tomada de las simulaciones Phet y denominada "Reflexión y refracción de la luz", explora la flexión de la luz entre dos medios con diferentes índices de refracción. Usa el apartado "Introducción" de la simulación y observa cómo cambiar el ángulo de felxión del aire al agua y al vidrio. Usa la herramienta del transportador para medir los ángulos y observa si puedes recrear la configuración del Ejemplo 8.2. También, usando el trasportador, confirma que el ángulo de reflexión es igual al ángulo de incidencia.
Ejemplo 8.3
Un gran cambio en la dirección
Supongamos que en una situación como la del ejemplo 8.2, la luz pasa del aire al diamante y que el ángulo incidente es de 30.0°. Calcula el ángulo de refracción θ2 en el diamante.
Estrategia
Nuevamente, el índice de refracción para el aire se toma como n1 = 1.00, y se nos da
58
θ2 = 30.0°. Podemos buscar el índice de refracción para el diamante en la tabla 8.1, encontrando n2 = 2.419. La única incógnita en la ley de Snell es θ2, que deseamos determinar.
59
 Comprueba tu aprendizaje 7.9
Comprueba tu aprendizaje 7.9
El estudio de la superposición de varias ondas tiene muchas aplicaciones interesantes más allá del estudio del sonido. En capítulos posteriores, discutiremos las propiedades de onda de las partículas. Las partículas pueden modelarse como un "paquete de ondas" que resulta de la superposición de varias ondas, donde la partícula se mueve a la "velocidad de grupo" del paquete de ondas.
7.7 El efecto Doppler
El sonido característico del zumbido de una motocicleta es un ejemplo del efecto Doppler. Específicamente, si estás parado en una esquina y observas una ambulancia con una sirena que suena a una velocidad constante, notarás dos cambios característicos en el sonido de la sirena. Primero, el sonido aumenta en intensidad cuando la ambulancia se acerca y disminuye en intensidad cuando se aleja, lo que se espera. Pero además, la sirena aguda cambia dramáticamente a un sonido de tono más bajo. A medida que pasa la ambulancia, la frecuencia del sonido que escucha un observador estacionario cambia de una frecuencia alta constante a una frecuencia inferior constante, aunque la sirena está produciendo una frecuencia de fuente constante. Cuanto más se acerque la ambulancia, más brusco será el cambio. Además, cuanto más rápido se mueva la ambulancia, mayor será el cambio. También escuchamos este cambio característico en la frecuencia de los automóviles, aviones y trenes que pasan.
El efecto Doppler es una alteración en la frecuencia observada de un sonido debido al
60
movimiento de la fuente o del observador. Vive este efecto en la siguiente escena interactiva, diseñada por Julio César Domínguez Tovar:
61
62
INTEGRANDO
CON PACO

INTERACTIVO
―Tiene razón profe. Créame que me ha servido esta sesión para despejar mi cabeza. Ahora atenderé mis otros problemas, los cuales son más simples. Hasta pronto profe.
―De acuerdo Paco, en el próximo apartado haremos ejercicios. Mientras te comparto un rompecabezas para que te alejes de tus problemas.
―Parece que le gustan mucho los juegos, profe.
―Así es Paco, disipa mi mente y me acerca a mi hijo, otro enamorado de los juegos.
―Gracias profe, trataré de relajarme con su jueguito.
―¡Juegazo! Paco... ¡Descansa!
64
Ejercicios del método de integración por partes
―Hola profe, me entretuve bastante con su ¡juegazo! Tiene razón, esas pausas que propone me ayudan a relajarme.
―Me alegra Paco que haya contribuido a tu bienestar. Ahora, dime si has practicado la nueva técnica de integración.
―¡Claro que sí!, recuerde que soy su alumno estrella.
―Eres "uuuuuno" de mis alumnos estrella.
―Le voy a imitar profe: "como dice el dermatólogo... vamos al grano". Estuve consultando algunos textos de Cálculo y me compliqué un poco, pues usan diferentes notaciones para las derivadas, recuerdo que en el curso de Cálculo Diferencial, usted nos advertía sobre ello. Me lo vuelve a explicar profe... please
―Ok Paco, no problem. The notation for differentiation can be written as...
―¡Oh, no!, profe, explíqueme en español. Yo manejo dos idiomas el español y el paisa4, pero de english... poco.
―Estaba bromeando Paco, te lo recordaré. En la explicación que te hice de la técnica de "integración por partes" usamos la función f(x) = u. Partiendo de esta función, pasaré a
65
―Una bonita muestra del potencial educativo de estas escenas interactivas. Pude comerme mi caramelito "x^2-0.6 " a rodajitas... ¡hum! qué ricas.
―Efectivamente todos estos objetos tienen esa característica intrínseca. En una imagen no es posible mostrar muchos atributos del objeto, pero en las escenas el
66
usuario puede cambiar esos atributos e intervenir en ellos. Yo, por ello, suelo llamarlos objetos interventivos.
Pero aprovecho esta escena para destacarte que también lo que se puede interpretar es que aproximamos la función f(x) por una función escalonada ―función constante a trozos― y a ésta es a la que le calculamos su área y al girarla le calculamos su volumen. La sencillez de las funciones escalonadas permite simplificar los cálculos y son de amplio uso en el análisis numérico y al tomar límite en el calculo integral. Otra alternativa es aproximar la función por funciones poligonales quedando el área reducida al cálculo de trapecios rectángulos y el volumen a troncos de conos.
―Sí comprendo la técnica y cómo las ideas sencillas son las más eficaces.
―Sí, y sin embargo aún teniéndolas delante de nuestros ojos no solemos verlas y es necesaria la abstracción y visión especial de un genio para que las alumbre y nos permita verlas a los demás. Es lo que tú decías antes, comemos y comemos muchos salchichones y sin embargo no somos capaces de detenernos en ver que lo hacemos poquito a poquito, a rodajitas, y un trocito más otro trocito hacen el total.
―¡Qué hambre! el hablar de comida siempre estimula los jugos gástricos...
―Pues no te voy a invitar a comer, pero sí a que calcules el volumen de helado que cabe en un cucurucho y el de la bola de helado que lo culmina. O dicho en lenguaje matemático, calcula el volumen de un cono de radio r y altura h, y el de una esfera de igual radio.
―Vaya profe yo soy de gustos tradicionales tangibles y no de sabores virtuales. Y no veo a nadie saboreando un helado y haciéndose esas preguntas que usted me hace.
―¡Ah! ¿no? Y que tal si fueras el empleado de una fábrica de helados y te preguntaran cuánto aumentaría el precio de los helados si se incrementara una décima parte el
67
68
Percepción
visual
INTERACTIVO
3.4 Las ilusiones de contexto
Las ilusiones visuales del grupo de investigación sobre la Ciencia Perceptual del Instituto Tecnológico de Massachusetts (MIT), liderado por Edward Adelson (Profesor de Ciencias de la Visión), se ha dedicado a la investigación de la percepción visual en brillo y transparencia, percepción de texturas, percepción de superficies, similitud perceptual, análisis de movimiento, entre otras líneas de investigación. La profesora Oliva (miembro del grupo) frente al tema de contexto expresa:
El contexto tiene efectos en múltiples niveles: semántico (una mesa y una silla se hallarán, probablemente en la misma imagen. No esperaríamos una mesa y un elefante), configuración espacial (un teclado se espera observarlo debajo de un monitor) y postura (Las sillas se esperan encontrar dirigidas hacia la mesa) (Oliva & Torralba, 2007).
70
3.4.1 Ilusión de Neblina. Nuestro cerebro tiende a asociar los objetos percibidos con los conocimientos previos adquiridos. El contexto o entorno en el cual se encuentra el objeto hace que nuestro cerebro le asigne propiedades de ese contexto al objeto percibido. Es decir, no percibimos el color y brillo reales, sino los calculados en comparación con el color y brillo de los objetos cercanos. Observa la ilusión de Neblina (Haze illusion) a continuación.
El efecto neblina se produce al superponer cuartos de círculos de color gris sobre un diamante (rombo) de un gris más claro (haz clic en el botón para verificarlo).
71
3.4.2 El anillo de Koffka. El psicólogo americano de origen alemán Kurt Koffka (1886-1941), fue uno de los fundadores de la psicología de la estructura o de la Gestalt junto con Max Wertheimer y Wolfgang Köhler. La ilusión de Koffka es un anillo gris se superpone en la mitad del fondo de una cortina de colores grises (diferentes del anillo), el anillo parece ser homogéneo. Sin embargo, si el anillo se divide levemente, las dos mitades del anillo parecen tener diferente tonalidad de gris (ver la escena interactiva siguiente). El principio de la Gestalt de la continuidad en la percepción visual explica este efecto.
72
Escher era un amante de las paradojas. En "la cascada" utiliza la ambigüedad de la representación bidimensional para ofrecernos un ejemplo de movimiento perpetuo. La inspiración le vino por la lectura de un artículo de R. Penrose en el que hablaba del tribar, una figura triángular tridimensional imposible (http://www.epsilones.com).
Para terminar este apartado, te proponemos que armes tu tribar en la siguiente escena interactiva, para ello, debes arrastrar los elementos de la ventana izquierda y configurar el tribar de Penrose que aparece en la ventana derecha.
73
3.8.2 Más figuras imposibles Reutersvärd
Además del tribar, existen cientos de figuras imposibles diseñadas por Oscar Reutersvärd28, algunas de ellas presentadas en la siguiente escena interactiva.
74
Las imágenes y muchas más se pueden consultar en la colección del programador ruso Vlad Alexeev
Ahora podemos comprender de dónde salió la inspiración de M.C. Escher.
75
5.3 Creatividad colombiana - la cocina oculta
El creativo Felipe Salazar y la diseñadora gráfica Karen Castañeda sorprenden en un periódico con un anuncio para el supermercado HiperCentro Corona ¿Puedes ver una cocina "3D" en la siguiente página?
© Felipe Salazar Rodríguez (Director Creativo) y Karen Castañeda (Directora de Arte)
Agencia: Leo Burnett Colombiana
76