
Tabla de contenido
de programación

Actividad del capítulo
Al terminar este capítulo, habrás resuelto los siguientes problemas:
Teorema del programa estructurado
Al leer los problemas planteados, quizá algunos se sientan desanimados, pues no esperaban nada de matemáticas y menos de programación. No obstante, como ser humano que eres siempre aplicas algo de lógica en tus decisiones, desde la simple decisión de ir al trabajo a la más compleja que es decidir sobre tu proyecto de vida. No te preocupes que este curso está diseñado para tratar conceptos básicos o, si se prefiere, elementales de programación. Sabías, por ejemplo, que Edsger Dijkstra, un experto en programación (considerado por algunos como el padre de la programación estructurada), nunca usó un ordenador para ejecutar y verificar sus algoritmos... pues, todo se reduce a la lógica... la lógica de programaciónAunque parezca irónico, Dijkstra, uno de los mayores desarrolladores de software de su época, evitó el uso de computadores en su trabajo durante décadas. Cuando, finalmente, sucumbió a la tecnología, únicamente utilizó los ordenadores para enviar correos electrónicos y hacer búsquedas en la red. Dijkstra nunca utilizó un computador para realizar ninguno de sus trabajos, todos ellos fueron realizados a mano. (crédito: https://es.wikipedia.org/wiki/Edsger_Dijkstra)..
Para que quedes más tranquilo, algunos científicos de la computación (Dijkstra, Jacopini, Böhm, von Neumann, ...), estuvieron de acuerdo en afirmar que todo programa se puede realizar combinando sólo tres estructuras lógicas o de control:
- Estructuras secuenciales
- Estructuras selectivas
- Estructuras iterativas o repetitivas.
La herramienta DescartesJS permite resolver los problemas anteriores, utilizando varias alternativas y con un código propio para elementos básicos como selección, lectura y escritura de datos.
En las estructuras iterativas, además del algoritmo clásico Hacer-Mientras (Do-While), el uso de familias en los selectores Gráficos, permite desarrollar actividades iterativas (repetitivas) que simplifica muchas situaciones.
Algoritmo
No hay consenso sobre la definición formal de "algoritmo", no obstante, en forma general, se puede decir que es un conjunto de instrucciones o reglas bien definidas, ordenadas y finitas que permiten llevar a cabo una actividad mediante pasos sucesivos que no generen dudas a quien deba hacer dicha actividad.
En matemáticas, lógica, ciencias de la computación y disciplinas relacionadas, un algoritmo (del griego y latín, dixit algorithmus y este del griego arithmos, que significa «número», quizá también con influencia del nombre del matemático persa Al-Juarismi) es un conjunto prescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permiten llevar a cabo una actividad mediante pasos sucesivos que no generen dudas a quien deba hacer dicha actividad. Dados un estado inicial y una entrada, siguiendo los pasos sucesivos se llega a un estado final y se obtiene una solución. En términos de programación, un algoritmo es una secuencia de pasos lógicos que permiten solucionar un problema. (https://es.wikipedia.org/wiki/Algoritmo).
Un algoritmo se puede representar de varias maneras: lenguaje natural, pseudocódigo, diagramas de flujo o en un lenguaje de programación. Para los problemas de este capítulo, usaremos el pseudocódigo y la herramienta DescartesJS para su solución.
Pseudocódigo
Permite la transición de la solución de nuestros problemas a un lenguaje de programación específico, el pseudocódigo es un conjunto
de pasos claros que permiten llegar a la solución de un problema. A continuación, iniciamos la solución de los problemas planteados al inicio de este capítulo.
Estructuras secuenciales
Una estructura secuencial es aquella en la que las instrucciones se ejecutan una después de la otra, en el orden en que están escritas, es decir, en secuencia. En una estructura secuencial se espera que:
se proporcione uno o varios datos, los cuales son asignados a variables para que con ellos se produzcan los resultados que representen la solución del problema que se planteó (https://www.uaa.mx).
Problema 1
A un estudiante se le aplican tres exámenes durante el semestre, cada examen tiene el mismo valor porcentual. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener el promedio de calificaciones.
Observa el pseudocódigo para la solución de este problema:
InicioLeer Nota1, Nota2, Nota3Hacer Suma = Nota1 + Nota2 + Nota3Hacer Prom = Suma/3Escribir PromFin
La secuencia o instrucción del tipo Hacer, como la cuarta instrucción del pseudocódigo anterior (Hacer Prom = Suma/3) es una asignación, que no se debe entender como una igualdad.
Su interpretación debe ser de la siguiente forma: "se realiza la operación Suma/3, el resultado se asigna a la variable Prom". Como lo hemos reiterado antes, la asignación funciona de derecha a izquierda.
Para evitar este tipo de confusiones, algunos programadores prefieren usar la siguiente convención:
Prom ← Suma/3
En lenguajes de programación como Pascal o Delphi: Prom := Suma/3 o en lenguaje C: Prom /= 3, siempre buscando evitar la confusión y comprender que asignaciones como c = c + 1 son completamentes válidasLa asignación c = c + 1 se conoce como contador, pues en una estructura iterativa (como veremos más adelante), a la variable c se le suma el valor de 1, N veces, es decir, si c es inicialmente cero, se le irá asignado los valores 1, 2, 3, ..., N..
Comprendido lo anterior, para ponernos a tono con la herramienta DescartesJS, en nuestros pseudocódigos usaremos la asignación Prom = Suma/3 (ver Figura 4.1)
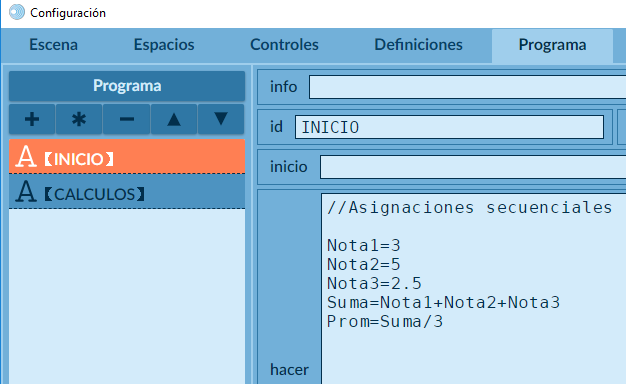
Puedes observar que hemos usado el selector Programa pues, obviamente, estamos programando. También habrás notado que elegimos el algoritmo INICIO evaluado una sola vez, pues para nuestro problema cumple con lo enunciado: Leer las notas y calcular su promedio.
Seguro ya estarás preguntándote qué ocurrió con las instrucciones Inicio, Escribir y Fin. Tanto Inicio como Fin, en una estructura secuencial, son convenientes en el pseudocódigo; sin embargo, en el código (programa) de DescartesJS se pueden omitir. En cuanto a la instrucción Escribir, debemos usar el selector Gráficos y agregar el gráfico texto pero, ... mejor observa el vídeo:
Pudiste observar que usamos un texto para escribir la solución de nuestro problema: Promedio = [Prom]. En DescartesJS las variables deben ir encerradas entre corchetes para que se muestre el valor de dicha variable. Por ahora, hemos usado un texto simple, más adelante veremos el texto enriquecido de DescartesJS, que permite presentar expresiones más elegantes o, si se prefiere, más atractivas.
Problema 2
Se tienen los tres lados de un triángulo. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener el área del triángulo (usa un control de tipo campo de texto).
El área de un triángulo dados sus lados $a$, $b$ y $c$, según la fórmula de Herón, es $\sqrt{s(s - a)(s - b)(s - c)}$, donde $s$ es el semiperímetro del triángulo $(a + b + c)/2$. Observa el pseudocódigo para la solución de este problema:
InicioLeer a, b, cs = (a + b + c)/2Area = $\sqrt{s(s - a)(s - b)(s - c)}$ Escribir AreaFin
Ya habíamos dicho que DescartesJS permite varias alternativas para resolver un problema, para este segundo problema usaremos dos alternativas, pero antes nos detendremos en la instrucción de entrada Leer, que en algunos lenguajes de programación se emplean palabras reservadas como input o read para ejecutar dicha instrucción.
En DescartesJS usaremos el control tipo campo de texto.
Control campo de texto
Veamos, entonces, cómo solucionamos el problema 2 con la herramienta DescartesJS.
- En primer lugar, creamos un nuevo objeto interactivo (Archivo → Nuevo) con dimensiones $400\times 400$ (selector Escena).
- En el selector Espacios al espacio
E1, que aparece por defecto, le desactivamos los checkboxejes,redyred10con el fin de eliminar el plano cartesiano de nuestro objeto. - Escribimos un título para el interactivo (opcional), para ello, en el selector Gráficos agregamos un gráfico tipo
textocon la siguiente configuración: - Escribimos el enunciado que pide el valor del lado
adel triángulo, para ello, en el selector Gráficos agregamos un gráficotexto, tal como lo muestra la siguiente imagen:
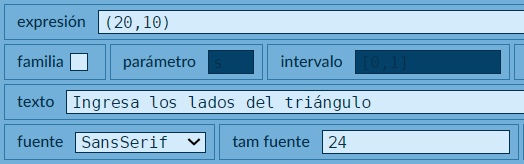
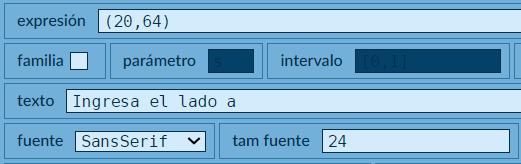
- Ahora, agregamos nuestro primer control numérico tipo
campo de texto(selector Controles), con la siguiente configuración: - Nuestro siguiente paso es escribir las instrucciones de asignación del pseudocódigo en el algoritmo
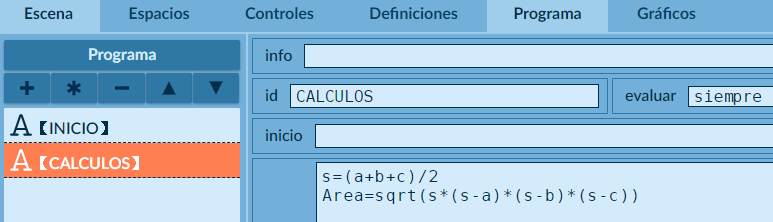
CALCULOS(selector Programa). Hemos seleccionado este algoritmo con evaluarsiempreporque podemos cambiar los valores de los lados en cualquier momento (siempre) y obtener una nueva área del triángulo (observa la Figura 4.2).
Realizamos el mismo procedimiento para los lados b y c (usa la opción copiar con el botón *) con las expresiones (20,124) y (20,184) respectivamente.
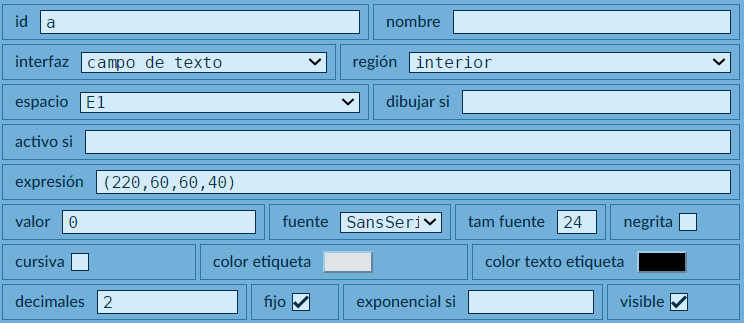
Igualmente para los otros dos controles con expresiones (220,120,60,40) y (220,180,60,40) respectivamente. Observa que el identificador de cada control (id) debe ser el nombre de la variable (a, b y c) que corresponde a los lados del triángulo, además de haber borrado el nombre del control.
El cálculo de la raiz cuadrada se puede hacer elevando a 0.5 la expresión (s*(s - a)*(s - b)*(s - c)) o usando la función sqrt(x).
- Finalmente, sólo nos resta agregar el texto que muestre la solución del problema (Área del triángulo), para ello, agrega un nuevo gráfico tipo
textocon la siguiente configuración:
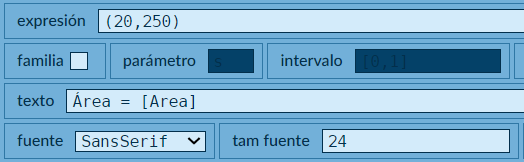
Puedes cambiar algunas propiedades, como el color y tamaño del texto.
Este es el objeto interactivo obtenido:
Prueba con el triángulo de lados $3$, $4$ y $5$, cuya área debe ser $6$. ¡Debes presionar la tecla Intro despues de ingresar el último lado!
Para los lados $b$ y $c$ hemos incluido el teclado virtual $7\times 2$ y $4\times 4$ respectivamente. El valor inicial de "c" lo hemos puesto con un contenido vacío (dos comillas simples), de tal forma que el ingreso de los datos no necesiten borrar el contenido inicial.
En la segunda alternativa vamos a usar dos controles tipo botón para que muestre el resultado, una vez hallamos ingresado los valores de los lados. Incluiremos, además, condicionales que activan o desactivan los campos de texto y los botones.
Cuando decimos que es una nueva alternativa es porque la estructura secuencial no la escribiremos en el selector Programa, sino en un parámetro del control botón. ¡Manos a la nueva obra!
- Inicialmente, pondremos un condicional en los controles tipo
campo de texto, es decir, en los controles para ingresar los ladosa,byc. Este condicional serámuestra = 0(ver la siguiente figura). - Ahora, vamos al selector Gráficos para hacer algunas modificaciones al último texto ingresado, el que muestra el resultado. En primer lugar, cambiaremos su posición por
(20,300), ello para abrir una área donde irá nuestro botón (oberva la siguiente figura).
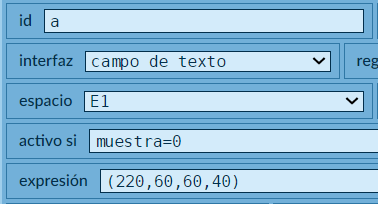
Esto significa que el campo de texto estará activo si la variable muestra es igual a cero. Por defecto, en DescartesJS todas las variables, no inicializadasEste término, ya aceptado por la academia de la lengua, significa establecer los valores inciales de un programa. La mayoría de lenguajes de programación exigen que las variables a utilizar en un programa, sean inicializadas, que incluye valores y tipo de dato, por ejemplo, a = 0 de tipo real., tendrán un valor de cero. lo que significa que al ejecutar el objeto interactivo, los campos de texto estarán activos.
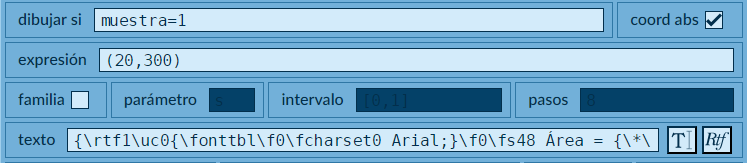
Ya sabemos que te estás preguntando ¿qué ocurrió con el texto?, ¿qué es esa expresión extraña? La respuesta es que hemos usado texto enriquecido, el cual se activa haciendo clic en el botón  , que nos mostrará el editor de textos enriquecidos:
, que nos mostrará el editor de textos enriquecidos:
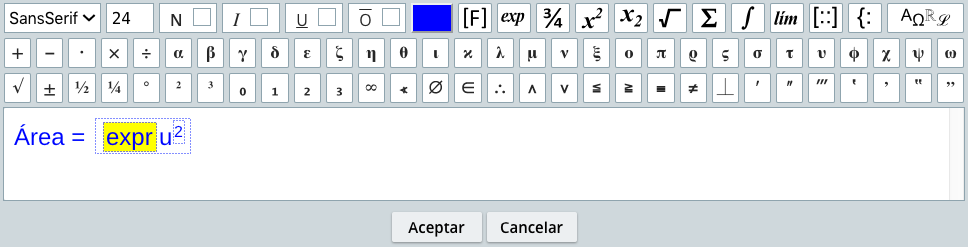
Hemos recurrido a este tipo de texto, porque el valor de una área debe estar en unidades cuadradas ($u^2$) y sólo con este tipo de texto es posible poner el exponente, usando el botón  ,
, expr debe contener el nombre de la variable Area. Bueno, por ahora, no has visto cuál es la alternativa, sólo habrás notado que estamos volviendo más elegante o, mejor dicho, más atractivo nuestro interactivo. ¡Vamos a ello!
- Agregamos un control tipo
botóncon esta configuración: el nombre esCalcular Áreaen laregión interior, expresión(125,250,150,30), colores a tu elección, tamaño de fuente en22.
- Luego... bueno, estamos cansados de escribir... mejor, observa:
Puedes observar que la alternativa existe porque el código del programa lo trasladamos a la acción calcular del control tipo botón. Observa, además, que una vez hacemos clic en el botón, a la variable muestra le asignamos el valor de 1, situación que inactiva los campos de texto y hace que aparezca el segundo botón. Una novedad más: le pusimos imagen de fondo al interactivo. Nota que usamos la función raíz cuadrada proporcionada por DescartesJS: sqrt (SQuare RooT).
Este es el objeto interactivo obtenido:
Problema 3
Dados dos puntos aleatorios del plano cartesiano. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener la distancia entre los dos puntos.
He aquí el pseucódigo
InicioObtener, aleatoriamente, $A(x_1, y_1)$ y $B(x_2, y_2)$ Distancia = $\sqrt{(x_2 - y_2)^2 + (x_1 - y_1)^2}$ Escribir Puntos y DistanciaFin
Una vez te expliquemos cómo generar números aleatorios, estarás en capacidad de programar la solución del problema en DescartesJS, con lo que hemos trabajado en los problemas anteriores. Por ello, no nos detendremos en mucho detalle como lo hemos hecho antes. Por otra parte, no nos limitaremos sólo a generar los puntos, calcular su distancia y mostrar resultados, pues es una gran oportunidad de usar las ventajas que nos ofrece DescartesJS. Así que, resolveremos el problema y mostraremos su solución tanto numérica como gráfica.
- Crea un nuevo objeto interactivo (Archivo → Nuevo), sin modificar sus dimensiones.
- Agrega un espacio (
id = E2) de ancho30%, desactivando los checkbox:ejes,red,red10ytexto. - Agrega un espacio (
id = E3) enx=30%,ancho=70%yescala=20. Activa el checkboxnúmeros.
Números aleatorios
Existe solamente una variable general de DescartesJS, que es rnd. Esta variable, cuyo nombre viene de random (o aleatorio), genera un valor aleatorio real entre $0$ y $1$ cada vez que es llamadaEn realidad, se genera un número entre 0 y 0.999....
Si queremos generar números aleatorios entre $1$ y $20$, usamos rnd*20 + 1 o -(rnd*20 + 1) si queremos generarlos entre $-20$ y $0$. Sumamos 1 porque rnd*20 genera números entre $0$ y $19.999...$
Continuemos, entonces, solucionando nuestro problema:
- En el espacio
E2, escribe el título del problemaDistancia entre dos puntos. - Un poco más abajo del título y en el espacio
E2, agrega un botón con nombreGenera puntosy activo simuestra=0, usa los colores y tamaño a tu gusto
Hasta aquí, debes tener un objeto como:
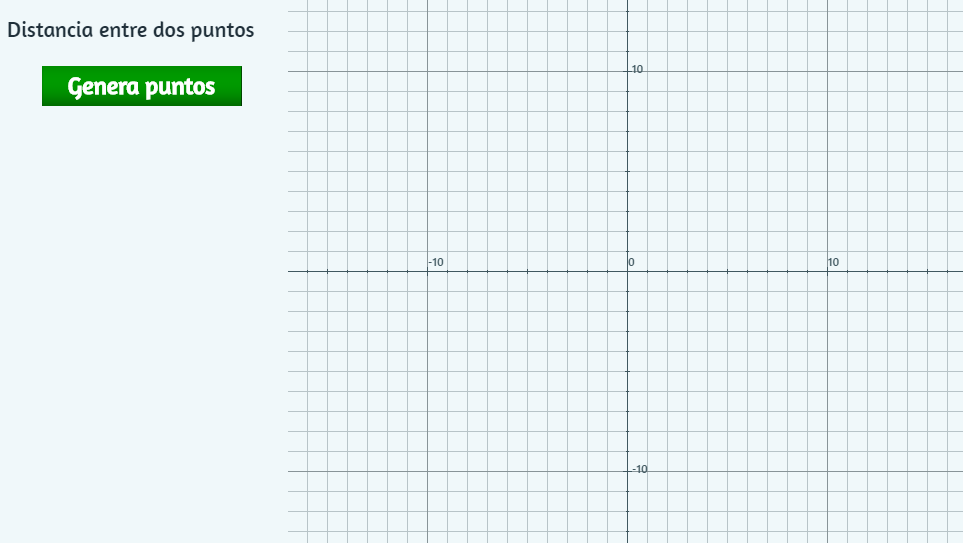
- En el botón elige la acción
calculary enparámetro, escribes:
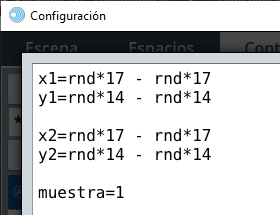
Observa que una vez se haga clic en el botón, suceden tres eventos. El primero es que se calculan las coordenadas de los dos puntos, si miras bien la gráfica del espacio E3, el eje $x$ muestra el intervalo [-17, 17] y el eje $y$ [-13, 13], por ello, hemos generado los números aleatorios entre esos valores; por ejemplo, para las abscisas con números aleatorios rnd*17 - rnd*17, que garantiza tanto números negativos como positivos. Es importante que comprendas que la expresión no se anula, pues cada uno de los términos genera un número diferente. El segundo evento es el que asigna 1 a la variable muestra. El tercero, consecuencia del anterior, es que se inactiva el botón.
- Un poco más abajo del botón, agregas el siguiente texto:
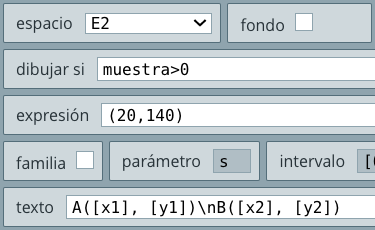
Observa que en el texto, las variables van encerradas entre corchetes. La expresión \n equivale a un salto de línea. Este texto aparecerá cuando el valor de la variable muestra es mayor que cero. Si analizas el resto del objeto interactivo, entenderás la expresión.
- Agrega un nuevo
botón, ubicado más abajo del texto anterior, con la misma configuración delbotónanterior, excepto por su posición, por la expresión enactivo si, que ahora esmuestra=1y por el nombre que es:Halla distancia. No olvides seleccionar el espacioE2.
- Seleccionas en acción
calculary en parámetros escribimos: - En el selector gráficos agregamos el texto
Distancia = [d] u, ubicado más abajo del botón anterior, que sólo se mostrará simuestra=2. - Nuestro último botón tendrá el nombre
Otro ejercicio, se mostrará simuestra=2y en acción seleccionamosinicio, que tiene como función reiniciar el interactivo.
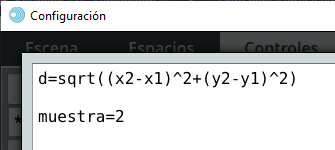
Ya tenemos todos los elementos del espacio E2, nos falta incluir los elementos gráficos del espacio E3.
- En el selector Gráficos agregamos un punto, con expresión
(x1,y1), que se mostrará solo simuestra>0. Se trata del punto $A$. Hemos elegido el colorrojoy el tamaño del punto en4. Similarmente, agregas el punto $B$. No olvides seleccionar espacioE3.
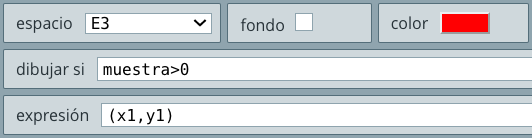
- Finalmente, en el selector Gráficos agregamos un
segmentocuya expresión es(x1,y1)(x2,y2), que corresponde a los puntos $A$ y $B$.
Este es el objeto interactivo obtenido:
Observa que al hacer clic sobre el plano cartesiano se muestran las coordenadas del punto sobre el que haces clic. También, puedes desplazar el plano con clic izquierdo sostenido o hacer zoom con clic derecho sostenido.
Estructuras selectivas
En los algoritmos, las estructuras selectivas o condicionadas son de la forma:
Si comparación verdadera
Entonces
Hacer acción 1
Sino
Hacer acción 2
Fin si
En un diagrama de flujo es, quizá, más fácil apreciar el proceso de selección en una estructura condicionada (observa la Figura 1.3).
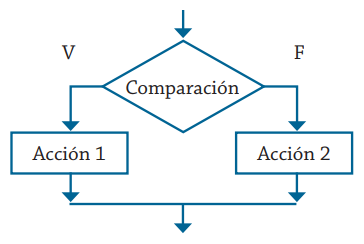
En DescartesJS, la estructura anterior se escribe así: comparación?accion1:acción2, donde la comparación usa operadores booleanos.
Por otra parte, las acciones 1 y 2, generalmente, devuelven el valor a una variable (var), por lo que la estructura selectiva en DescarteJS sería de la forma: var = comparación?accion1:acción2. Los operadores booleanos en DescartesJS, los puedes consultar en este texto:
Problema 4
Dado dos números. Elabora un pseudocódigo y ejecútalo en DescartesJS para obtener el número mayor.
El pseudocódigo para este problema clásico, sería:
InicioLeer dos números A, BSi A>B Entonces Mayor=A Sino Mayor=B Fin siEscribir número mayorFin
El objeto interactivo en DescartesJS, correspondiente a este pseudocódigo, excepto por la instrucción 3, ya lo sabes diseñar. Veamos cómo construyes el condicional.
Puedes usar el algoritmo CALCULOS del selector Programa o el parámetro de la acción calcular de un control tipo botón. Nosotros hemos usado la segunda alternativa, así:
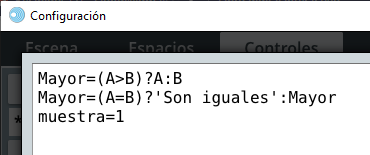
La primera línea Mayor=(A>B)?A:B, es fácil de comprender. Si la comparación es verdadera (A>B), el número mayor es A, sino es B. La segunda línea responde a la situación donde los dos números son iguales, asignando a la variable Mayor una cadena de caracteres: 'Son iguales', ¡Fácil! ¿No?
El objeto interactivo quedaría así:
Una novedad en este diseño es la reducción de decimales, tanto en los campos de texto como en el texto de respuesta, a cero cifras decimales.

Problema 5
Dado un número. Elabora un pseudocódigo y ejecútalo en DescartesJS para determinar si el número es de tres cifras (usa campo de texto).
Supondremos que el número es un entero. Así las cosas, el pseudocódigo es:
InicioLeer un número entero NSi (N > 99) y (N < 1000) Entonces Rta = "Es de tres cifras" Sino Rta = "No es de tres cifras" Fin siEscribir respuesta (Rta)Fin
Tarea (parte 1)
Resuelve el problema 5 en DescartesJS. Ten en cuenta que la comparación del Si se escribe así: (N > 99)&(N < 1000).
Problema 6
En un almacén se tiene la siguiente promoción: todo artículo con un precio superior a $\$25,000$ tendrá un descuento del $20\%$, los demás tendrán el $10\%$. Elabora un pseudocódigo y ejecútalo en DescartesJS para determinar el precio final que debe pagar una persona por comprar un artículo y el valor del descuento.
Otro problema sencillo que puedes resolver, sólo recuerda que si el artículo vale $\$30,000$, el descuento será: 30000*20/100.
Tarea (parte 2)
Resuelve el problema 6 en DescartesJS.
Problema 7
Se tiene el nombre y la edad de tres personas. Se desea saber el nombre de la persona de mayor edad. Elabora el algoritmo correspondiente y ejecútalo en DescartesJS. Una alternativa es usar estructuras selectivas anidadas; sin embargo, para este nivel, hemos optado por un pseudocódigo simple como el siguiente:
InicioLeer los nombres N1, N2 y N3Leer las edades Ed1, Ed2 y Ed3Si (Ed1 > Ed2) y (Ed1 > Ed3) Entonces PersonaMayor = N1 Sino PersonaMayor = PersonaMayor Fin siSi (Ed2 > Ed1) y (Ed2 > Ed3) Entonces PersonaMayor = N2 Sino PersonaMayor = PersonaMayor Fin si
continua en la siguiente página.
Si (Ed3 > Ed1) y (Ed3 > Ed2) Entonces PersonaMayor = N3 Sino PersonaMayor = PersonaMayor Fin siEscribir el nombre de la persona mayorFin
Si haces un análisis del comportamiento del algoritmo, te darás cuenta que siempre encontrará el nombre de la persona mayor. Obviamente, partimos del supuesto de edades diferentes.
El problema original también pide la edad de la persona mayor, lo cual se puede hacer con tres instrucciones similares a las anteriores, pero cambiando la acción del Si verdadero por EdadMayor = N1, N2 o N3, según la comparación correspondiente.
En DescartesJS el algoritmo, para las dos preguntas, sería así:
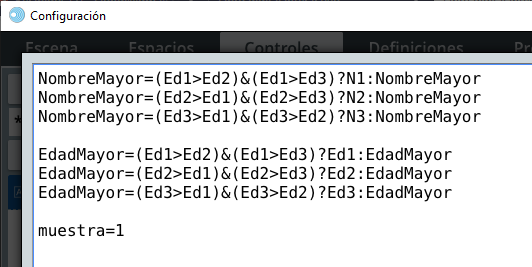
Centrado de textos en DescartesJS
Aprovechamos la solución de este problema, para abordar, de nuevo, el gráfico texto. Habíamos visto que los controles y los textos se posicionan en un espacio 2D de acuerdo a unas coordenadas (expresión), que se miden a partir de la esquina superior izquierda del espacio. Además, que la ordenada es positiva de arriba hacia abajo, contrario a como funciona el plano cartesiano, estas coordenadas, así establecidas, se llaman coordenadas absolutas. No obstante, DescartesJS permite el uso de coordenadas relativas, que funcionan de acuerdo al plano cartesiano. Usaremos esta propiedad para el diseño de la solución de nuestro problema.
En primer lugar, crea un objeto interactivo (Archivo → Nuevo) con dimensiones $600\times 500$ pixeles (selector Escena). A continuación, crea un texto (selector Gráficos), tal como aparece en la Figura 1.4.
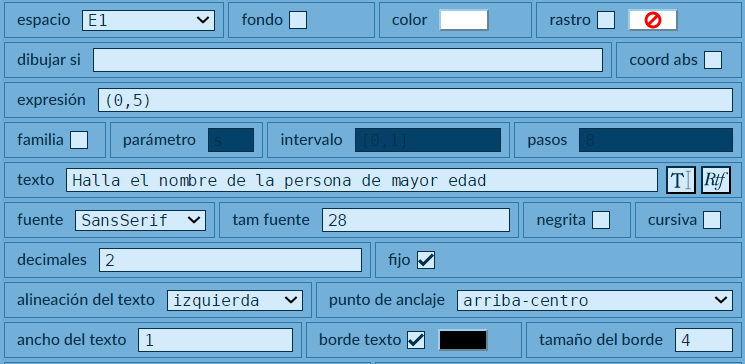
En la Figura 1.4 puedes observar que hemos desactivado el checkbox de coord abs (coordenadas absolutas), lo que quiere decir que hemos activado las relativas. En el objeto que has creado, escribe el texto Hallar la persona de más edad en la posición (0,0) ¿qué ocurre? Luego, modifica el punto de anclaje, ¿qué concluyes? Observa la Figura 1.5, en la cual aparecen varias opciones y, finalmente, el texto centrado en las coordenadas (0,5) con punto de anclaje arriba-centro.
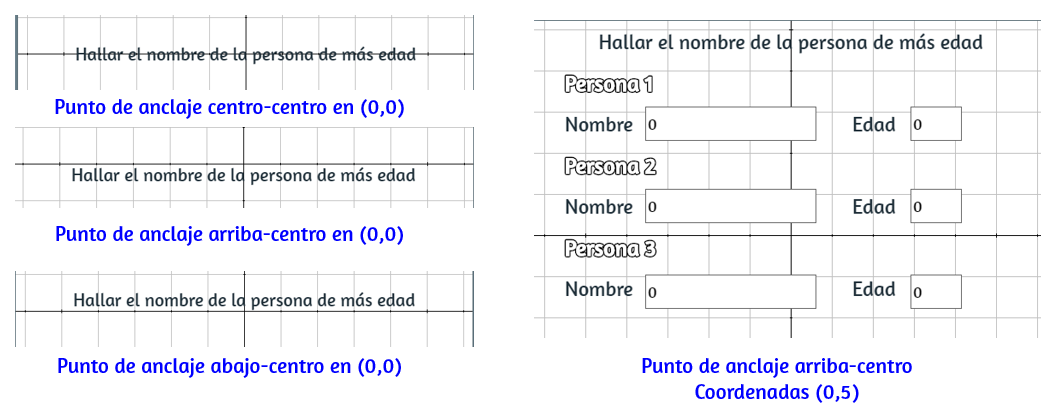
Ahora el texto lo posicionamos en el espacio de acuerdo a las coordenadas cartesianas, los demás textos de la Figura 1.5 se diseñaron usando estas coordenadas, lo cual nos lleva a concluir que no debemos desactivar el plano cartesiano, hasta no terminar nuestro diseño.
El objeto interactivo, finalmente diseñado, nos ha quedado así:
El efecto especial en el título y otros textos se logra activando el checkbox borde texto.
Puedes ingresar los datos usando la tecla de tabulación para cambiar entre los campos de texto y al final presiona la tecla intro, para activar el botón Calcular. Trata de obtener este objeto interactivo con lo que has aprendido.
Estructuras iterativas
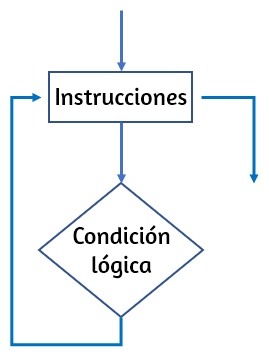
Una estructura iterativa o de repetición es aquella que permite que un proceso o conjunto de acciones se realice de manera cíclica (loop o bucle). Este proceso repetitivo se realiza mientras una condición lógica sea verdadera. Existen cuatro formas comunes de este tipo de estructuras: "Hacer mientras" (Do-While), "Mientras que", "Repite hasta que" y "Desde, hasta" (For-next). En este apartado sólo trabajaremos con la primera forma, pues es la que usa DescartesJS. En la Figura 1.6 se presenta la forma Do-While en un diagrama de flujo.
Problema 8
Elabora un pseudocódigo y ejecútalo en DescartesJS para calcular la suma de los $100$ primeros números naturales (no uses la fórmula directa).
El pseucódigo para resolver este problema, es el siguiente:
Inicioc ← 0S ← 0Hacer c ← c + 1 S ← S + c Mientras c < 100 Fin HacerEscribir SFin
Hemos usado el caracter ← para recordar la instrucción tipo asignación. Si bien DescartesJS inicializa las variables no declaradas en cero, las hemos declarado, sólo para observar cómo se puede hacer en una estructura Hacer-Mientras de DescartesJS que, para este problema, se muestra en la siguiente figura:
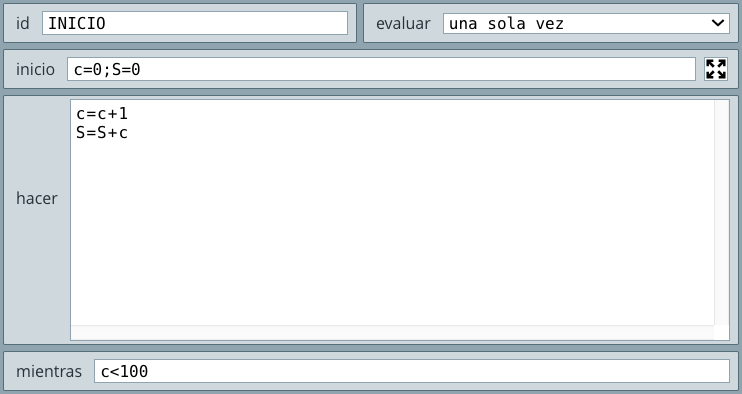
Hemos usado el algoritmo INICIO del selector Programa, del cual explicamos:
- En el cuadro de texto de
inicio, inicializamos las variablescySen cero (cada instrucción separada por un punto y coma). Estas variables corresponden a un contador de números (c) y a la suma de esos números (S). - En el cuadro de texto
hacerescribimos las acciones a repetir. La primera esc = c + 1, que tiene como función contar números así:c = 0 + 1,c = 1 + 1,c = 2 + 1,... que asigna aclos números1,2,3,... La segunda tienen como función sumar esos números así:S = 0 + 1,S = 1 + 2,S = 3 + 3,..., es decir, suma aSlos números naturales desde1hasta100(el número que hace la condicon falsa). - En el cuadro de texto
mientrasponemos la condiciónc<100.
Sólo nos resta escribir S, que en DescartesJS lo logramos con el gráfico texto del selector Gráficos, así:

Al ejecutar (Aplicar) el objeto interactivo, nos aparece:

Problema 9
En un archivo se tienen los datos de la estatura de un grupo de $15$ estudiantes. Elabora un pseudocódigo y ejecútalo en DescartesJS para calcular la estatura promedio (usa un vector de estaturas).
El pseudocódigo que soluciona este problema es el siguiente:
Inicioi = 0S = 0Hacer i = i + 1 Leer Estatura S = S + Estatura Mientras i < 15 Fin HacerEscribir S/15Fin
En DescartesJS creamos el interactivo así:
Antes de explicar el algoritmo usado por DescartesJS, te recomendamos leer el siguiente texto:
Tal como lo observaste en el vídeo o lo consultaste en el texto, una forma de evitar el ingreso o lectura de $15$ variables es el uso de vectores. En este caso, desde el selector Definiciones, agregamos un vector identificado como E. A cada elemento E[i] del vector E le
asignamos una estatura. Quizá se nos olvidó definir el tamaño del vector, que tendría que ser 16, pues el elemento E[0] también cuenta, este olvido no impidió que el interactivo funcionara, pero es más correcto dimensionar el vector.
A continuación, desarrollamos el código de nuestro problema usando el algoritmo INICIO en el selector Programa. Las variables que usamos fueron un contador i y S para calcular la suma de las edades. En el caso de S, observa que le sumamos los elementos del vector E, así:
Seise inicializan en cero.- Mediante la instrucción
i = i + 1, aise le asigna el valor de0 + 1, o sea1. - Mediante la instrucción
S = S + E[i]que, en este paso, equivale aS = S + E[1]o, de acuerdo a los valores de los elementos del vector,S = S + 1.45 - Tal como lo dice el pseudocódigo, el próximo paso es evaluar la condición del mientras
i < 15, que en este momento es verdadera, por lo que se repite el proceso, hasta que la condición sea falsa, es decir, hasta queisea igual a15, lo que garantiza que se sumen las15estaturas. - Finalmente, obtenemos el promedio de edades, dividiendo la suma por
15.
Problema 10
Se requiere un algoritmo para determinar, de N cantidades, cuántas son menores o iguales a cero y cuántas mayores a cero. Realiza el pseudocódigo y ejecútalo en DescartesJS para resolver el problema.
Bueno... esa es la tercera parte de la tarea 3.
Aplicación
Algoritmos de ordenamiento
La siguiente unidad interactiva del proyecto Un_100, diseñada por Joel Espinosa Longi, presenta algoritmos de ordenamiento de burbuja, por inserción, por mezcla y rápido.
En el apartado de cierre, Joel muestra los códigos que incluyen las tres estructuras trabajadas en esta sesión.
El vídeo de motivación hay que verlo directamente en YouTube, pues el propietario del canal restringió la opción de "embeberlo".
¡Hasta la próxima sesión!
