Mostrando artículos por etiqueta: 14 a 16 años
En la siguiente entrevista que podrás escuchar a través de Radio Descartes, podrás disfrutar de la experiencia que nos cuentan los componentes del departamento del IES San Paio de Tui en Pontevedra. El más grande de los 2 centros públicos del municipio, cuenta con 4 grupos por nivel de 1ºESO a 2ºBachillerato, con unos 650 alumnos en total. En él casi todos los miembros del departamento de Matemáticas utilizan los materiales de Descartes y hoy nos animan a conocerlos y probarlos.
La entrevista la ha realizado Emilio Pazo en nombre de sus compañeros a los que les damos las gracias desde aquí por compartir su experiencia con nosotros. Los nombres de los profesores que forman el departamento son:

Hubo un tiempo en el que los dragones podían aprender a sumar y restar. Un abuelo y su nieto descubren todos los misterios de la geometría. Un diablillo nos ayudará a vencer el miedo a las matemáticas llevándonos a un sin fin de aventuras. Por último, un árabe en un viaje por tierras exóticas se halla sujeto a pruebas que irá resolviendo con sus conocimientos de matemáticas.
¿Qué tal te ha sonado todo lo anterior? Si te parece interesante, puedes descubrir un mundo lleno de aventuras en cada uno de los libros que vas a ver a continuación en el vídeo. Hay un libro para cada una de las etapas educativas: Primaria, Secundaria y Bachillerato.
Llega el mes de septiembre, la vuelta al cole se acerca. Los nuevos libros, los colores sin estrenar, los cuadernos en blanco preparados para llenarse de nuevas ideas,... ¡Todo nuevo! Nosotros seguimos con las lecturas. Este es tan buen momento como otro para seguir leyendo. Recomendemos a nuestros alumnos un libro que curiosamente tenga que ver con las matemáticas, seguro que más de uno se sorprende.
En esta ocasión, tenemos un libro para los niños de primaria donde descubrirán un número que se vuelve loco. En el segundo libro descubriremos cómo es posible convivir en una misma ciudad donde confluyeron las tres grandes religiones, ¿tendrán algo que ver las matemáticas en esa convivencia? Un nuevo paseo por la ciudad nos mostrará gran cantidad de números y por último, un libro que nos mostrará la vida de un estudiante de matemáticas inmerso en Alemania durante la segunda guerra mundial.
Todos los detalles los puedes ver en el siguiente vídeo.
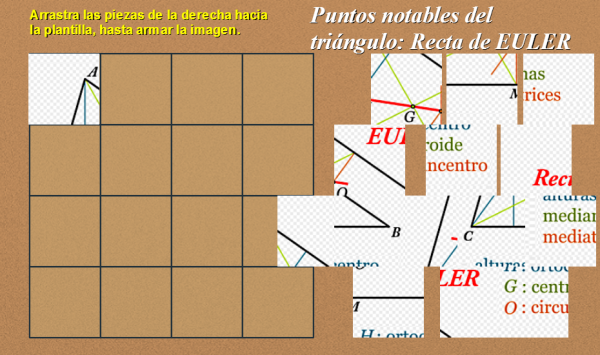
Una vez publicados los artículos de esta serie de puntos notables del triángulo (Ortocentro, Baricentro, Circuncentro e Incentro) concluimos en éste con una propiedad interesante: Se trata de la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro ó centroide y el circuncentro que es motivo para nuevas reflexiones sobre la geometría del triángulo.
Utilizamos como recurso didáctico, al igual que en los anteriores casos, un puzle de arrastre que cuando se arma se muestran algunas observaciones y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede encontrar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y el visionado de un vídeo.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, todos estos materiales se integrarán en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y formará parte de la Miscelánea en la sección de Materiales de esta Web.
En los tres artículos publicados anteriormente de esta misma serie hemos tratado y por este orden el Ortocentro, el Baricentro y el Circuncentro.
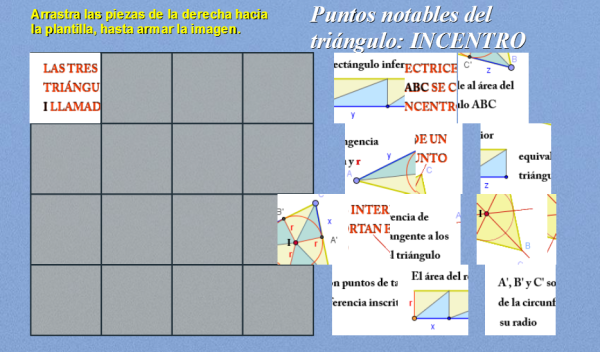
Con el Incentro, que hoy es el motivo de este artículo, terminamos la serie de puntos notables que estaba prevista.
Utilizamos como recurso didáctico, al igual que en los anteriores casos, un puzle de arrastre que una vez armado muestra una imagen donde intervienen como elementos de la composición las bisectrices interiores a un triángulo, el incentro, la circunferencia inscrita y texto. Además cuando se completa el puzle se repasa la definición de bisectriz y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede encontrar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y de Geogebra y con las explicaciones que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, se integrarán todos estos materiales en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y donde además se pondrá como reto armar un nuevo puzle para obtener la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro y el circuncentro que será motivo para nuevas reflexiones sobre la geometría del triángulo.
En los dos artículos publicados anteriormente de esta misma serie hemos tratado y por este orden el Ortocentro y el Baricentro.
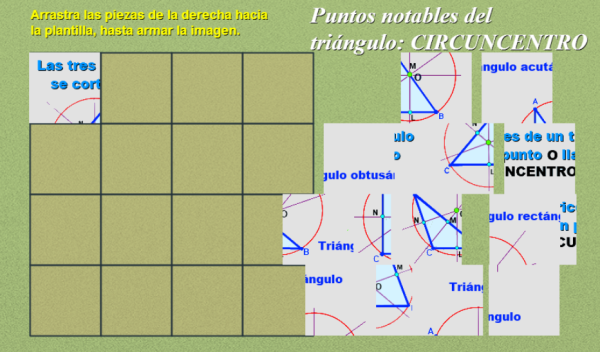
Como continuación, hoy le toca el turno al Circuncentro. Utilizamos como recurso didáctico un puzle de arrastre que una vez armado muestra una imagen de su representación gráfica en tres casos según que el triángulo donde se construye sea acutángulo, rectángulo u obtusángulo. Además cuando se completa el puzle se repasa la definición de mediatriz y se enumeran algunas propiedades que invitan a la reflexión y a visitar dos materiales de consulta donde se puede dar respuesta a distintas cuestiones a través de la interacción con las escenas de DescartesJS y las explicaciones más detalladas que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, se integrarán todos estos materiales en una unidad que llevará por título “Puzles geométricos: Puntos notables del triángulo” y donde además se pondrá como reto armar un nuevo puzle para obtener la Recta de Euler, donde se sitúan curiosamente el ortocentro, el baricentro y el circuncentro que será motivo para nuevas reflexiones sobre la geometría del triángulo.
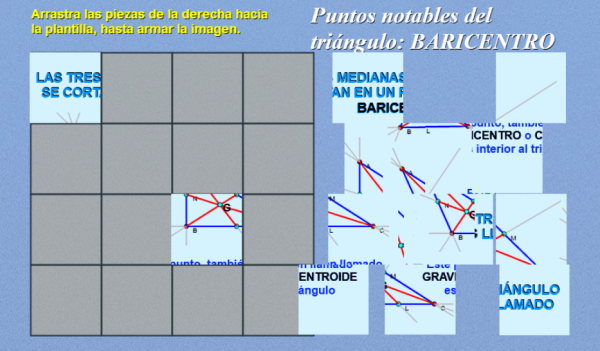
Continuamos en este artículo con la serie de puntos notables del triángulo tal como anunciábamos la semana anterior cuando presentábamos el Ortocentro. Hoy hemos elegido el Baricentro que también suele denominarse Gravicentro y Centroide según diferentes textos donde se consulte.
Se utiliza el puzle como recurso didáctico construido con DescartesJS. Cuando el puzle queda armado se observa una imagen de la posición que ocupa el baricentro en cada uno de los tres tipos de triángulo -rectángulo, acutángulo y obtusángulo- donde se dibujan las tres medianas, indicándose que en los tres casos el punto de corte, el baricentro, es interior. En este momento se repasa el concepto de mediana como recta y como segmento, se enumeran algunas propiedades que invitan a la reflexión y se proporcionan los enlaces a los materiales de consulta donde se puede dar respuesta a distintas cuestiones a través de la interacción con las escenas y las explicaciones más detalladas que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, integraremos todos estos materiales en un único cuerpo didáctico que llevará por título “Puzles geométricos: Puntos notables del triángulo”.
Continuamos jugando en verano. En esta ocasión utilizaremos unas cuantas fichas de dominó. Pero no vamos a jugar al dominó clásico. En esta ocasión y en cada juego aparecerán unas cuantas fichas que estarán relacionadas de algún modo. Tienes que encontrar la relación existente e indicar cuál es la ficha que falta. Busca la relación en el orden de las fichas, en alguna operación que hagas,...
El juego se llama: Adivina qué ficha falta. En el siguiente vídeo puedes ver cómo se juega y donde podemos encontrar más juegos parecidos.
El juego lo recomendamos para niños de entre 12 y 16 años. Es muy entretenido y una excelente gimnasia mental.
Enlace al juego on-line: https://proyectodescartes.org/miscelanea/materiales_didacticos/domino-JS/index.html
Puedes descargarlo para jugar en local: https://proyectodescartes.org/miscelanea/todos.htm
Para ver la presentación que aparece en el vídeo más tranquilamente, haz clic en la siguiente imagen.
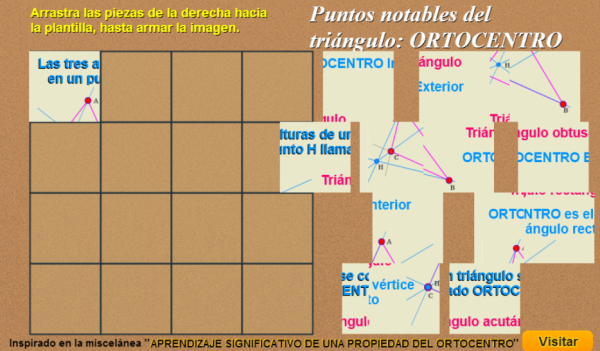
Este trabajo es el primero de una serie que se irá publicando sucesivamente. Se pretende hacer una revisión de los puntos notables de un triángulo: ortocentro, baricentro, incentro y circuncentro.
Se utilizará el puzle como recurso didáctico construido con DescartesJS y que una vez armado producirá una serie de consultas a materiales didácticos procedentes de diferentes subproyectos: Miscelánea, Unidades Didácticas, Un_100…
En el caso que nos ocupa ahora, cuando el puzle queda armado se observa una imagen de la posición que ocupa el ortocentro según que el triángulo donde se dibujan las alturas sea acutángulo, rectángulo u obtusángulo. En este momento se repasa el concepto de altura como recta y como segmento, se enumeran algunas propiedades que invitan a la reflexión y se proporcionan los enlaces a los materiales de consulta donde se puede dar respuesta a distintas cuestiones a través de la interacción con las escenas y las explicaciones más detalladas que allí se recogen.
La siguiente imagen lleva un enlace al puzle que se abrirá en una nueva ventana.
Una vez completada la publicación de la serie de puntos notables del triángulo, podremos pensar en integrar todos estos materiales en un solo cuerpo didáctico que llevará por título “Puzles geométricos: Puntos notables del triángulo”.
Últimos Comentarios
-
 Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
Excelente contribución a la educación global. Felicitaciones a los organizadores…
Escrito por Ageleo Justiniano Tucto
en %PM, %20 %503 %2023 %13:%Oct
Participantes de tres continentes en el curso para el diseño de libros interactivos
(Difusión)
-
 Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Estimado Javier Arturo: Agradecemos su reconocimiento al programa de Educación…
Escrito por José Antonio Salgueiro González
en %PM, %22 %458 %2023 %12:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
Me parece una gran iniciativa en favor de la educación,…
Escrito por JAVIER ARTURO MARTINEZ FARFAN
en %AM, %22 %189 %2023 %05:%Sep
Abierto el plazo de inscripción en la V Edición del Curso para el Diseño de Libros Interactivos
(Difusión)
-
 Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
Ildefonso era un hombre de edad y motivaciones educativas similares…
Escrito por José Luis San Emeterio
en %PM, %05 %805 %2023 %20:%Ago
Ildefonso Fernández Trujillo, in memoriam
(Difusión)
-
 Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)
Yo conocí la fórmula más bella de las matematicas como…
Escrito por Pepin
en %PM, %17 %576 %2023 %14:%Jul
Cálculo diferencial e integral, módulo I
(iCartesiLibri)



 CONTACTO
CONTACTO
