La posibilidad de comunicar escenas Descartes con páginas html facilita incorporar resultados obtenidos de la ejecución de comandos Geogebra e incluso construcciones completas que pueden ser manipuladas desde la propia escena.
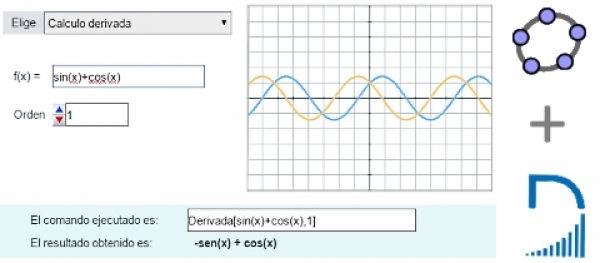
En este artículo se presenta una primera escena de ejemplo que utiliza los resultados de tres comandos Geogebra: Derivada, Integral y Circunferencia. Estos tres comandos tienen en común que su ejecución devuelve un único valor que puede enviarse a la escena Descartes como una cadena de caracteres. En próximos artículos se verá cómo incorporar los resultados de comandos que devuelven una lista de datos o una lista de listas.
Para poder comprender el código con el que se establece la comunicación desde Descartes, se recuerda la sintáxis de los comandos Geogebra que se utilizan en este ejemplo:
- Derivada[función,orden].
Por ejemplo: Derivada[cos(x),2] calcula la segunda derivada de la función cos(x)
- Integral[función,extremo_Inf,extremo_Sup].
Por ejemplo: Integral[cos(x),1,2] calcula la integral definida de la función cos(x) en el intervalo [1,2]
- Circunferencia[Punto1,Punto2,Punto3].
Por ejemplo: Circunferencia[(0,0),(1,1),(2,2)] calcula la ecuación de la circunferencia que pasa por los puntos A=(0,0), B=(1,1) y C=(2,2).
La escena Descartes que se presenta en este artículo incluye cuatro espacios.
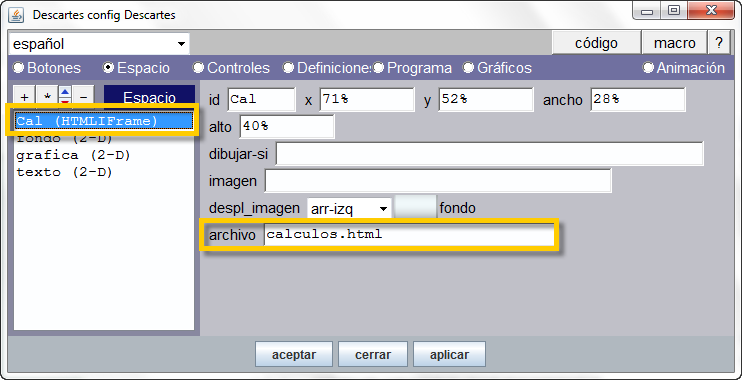
Uno de ellos es un espacio HTMLFrame que tiene como identificador el nombre Cal y será el que permitirá la comunicación con la página calculos.html que está vinculada a este espacio a través del parámetro 'archivo'.
La página calculos.html incluye el código javascript necesario para poder enviar y recibir datos de la construcción Geogebra que está embebida en ella. Esta página no necesita ser modificada y debe incorporarse en el mismo directorio que la página que contenga la escena Descartes (de no ser así se tendrá que modificar la ruta de acceso a ella en el parámetro 'archivo' del espacio HTMLFrame).
El funcionamiento de la escena Descartes que se presenta como ejemplo es sencilla. Elegida una de las tres opciones del menú, se inicia la comunicación con Geogebra. Si la opción elegida del menú es 'Calculo de la Derivada' se ejecuta la función Calculo1(), si se elige la opción 'Circunferencia por tres puntos' la función a ejecutar será Calculo2() y en el caso de que la opción sea 'Cálculo de la integral de un intervalo' la función asociada es Calculo3().
Las tres funciones tienen un código similar, en primer lugar construyen una cadena de caracteres con la sintásis del código Geogebra a ejecutar y después inician la comunicación enviando a la página incluida en el espacio Cal el evento 'evalua' pasándole como parámetro esta cadena de caracteres. Por ejemplo, el código incluido en la función Calculo1() es el siguiente:
n1='Derivada['+f+','+orden+']'
Cal.set('evalua',n1)
A la hora de generar la cadena de caracteres n1 se ha utilizado los valores de f y orden que están vinculados a los dos controles que se muestran en la escena para modificar, respectivametne, la expresión de la función y el orden de la derivada.
La página calculos.html, que está asociada al espacio Cal, recibe entonces el mensaje y ejecuta el código asociado al evento 'evalua' tras lo cual devuelve a la escena Descartes el resultado en una cadena de caracteres que siempre tiene por nombre vCalculado.
Todo este proceso es totalmente transparente al autor de la escena que puede utilizar el valor de la variable vCalculado de la misma forma que cualquier otra variable creada en la propia escena. Así, si por ejemplo se quiere representar la función derivada obtenida tras ejecutar Calculo1(), bastaría con:
- Evaluar la cadena de caracteres que se ha devuelto con el valor de la derivada: f1=_Eval_(vCalculado)
- Definir una función fun1(x)=f1 para poder crear un objeto gráfico de tipo ecuación cuya expresión sea: y=fun1(x)
Se puede practicar con la escena descargándola del siguiente enlace: Ejemplo1_CAS-JS.zip