Física - Volumen III
INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo
Red Educativa Digital Descartes
Fondo Editorial RED Descartes

Córdoba (España)
2022
Título de la obra:
Física - Volumen III
Segunda edición
Autor:
José Gregorio Doria Andrade
Juan Guillermo Rivera Berrío
Obra derivada del libro (University Physics - Volume III)
Samuel J. Ling (Truman State University)
Jeff Sanny (Loyola Marymount University)
Bill Moebs
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Diseño de cubierta: Margarita Patiño Jaramillo
Fuentes: Livvic y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Núcleo del libro interactivo: julio 2022
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
https://prometeo.matem.unam.mx/recursos/VariosNiveles/iCartesiLibri/
ISBN Obra completa: 978-84-18834-39-4
ISBN Volumen III: 978-958-56476-9-5
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Este libro digital interactivo se ha diseñado con fundamento en la filosofía del Proyecto Descartes: "Trabajando altruistamente por la comunidad educativa de la aldea global", que sólo busca desarrollar contenidos educativos para el provecho de la comunidad académica, esperando únicamente como retribución el uso y difusión de estos contenidos. El contenido del libro, al igual que los objetos interactivos se han diseñado de tal forma que se puedan leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin. El libro se puede descargar para su uso en local sin dependencia con la red, a excepción de los ocho vídeos incluidos en el texto.
El contenido del libro se basa en un recurso de OpenStax, organización sin fines de lucro de la Universidad de Rice, cuya misión, similar a la nuestra, es mejorar el acceso de los estudiantes a la educación. El libro ha sido desarrollado para cumplir con el alcance y la secuencia de la mayoría de los cursos de física universitarios y proporciona una base para una carrera en matemáticas, ciencias o ingeniería.
Este tercer volumen del libro de texto de Física Universitaria se adhiere al alcance y la secuencia de cursos de física en segundo o tercer nivel universitario. Se ha trabajado para hacer que la física sea interesante y accesible para los estudiantes, manteniendo el rigor matemático inherente a la materia. Con este objetivo en mente, el contenido de este libro de texto ha sido desarrollado y organizado para proporcionar una progresión lógica de conceptos fundamentales más avanzados, basándose en lo que los alumnos ya han aprendido y enfatizando las conexiones entre los temas y entre la teoría y las aplicaciones. El objetivo de cada sección es permitir que los estudiantes no solo reconozcan conceptos, sino que trabajen con ellos de manera que sean útiles en cursos posteriores y carreras futuras. La organización y las características pedagógicas fueron desarrolladas y revisadas con comentarios de educadores de ciencias dedicados al proyecto.
A lo largo del libro encontrarás derivaciones de conceptos que presentan ideas y técnicas clásicas, así como también aplicaciones y métodos modernos. La mayoría de los capítulos comienzan con observaciones o experimentos que colocan el material en un contexto de experiencia física. Las presentaciones y explicaciones se basan en años de experiencia en el aula por parte de profesores de física de larga data, que luchan por un equilibrio de claridad y rigor que ha demostrado ser exitoso con sus alumnos. Las figuras históricas clave y los experimentos se discuten en el texto principal, manteniendo un enfoque en el desarrollo de la intuición física. Las ideas clave, las definiciones y las ecuaciones se destacan en el texto.
Los ejemplos y las imágenes de apertura de capítulos a menudo incluyen aplicaciones contemporáneas de la vida cotidiana o de la ciencia y la ingeniería modernas con las que los estudiantes se pueden relacionar, desde teléfonos inteligentes hasta Internet y dispositivos GPS.
El texto original, desarrollado por Ling, Sanny y Moebs, ha sido publicado en versiones html y pdf. Esta nueva versión, diseñada por Rivera, presenta las siguientes aportaciones: traducción al español, diseño en formato flipbook, incorporación de 48 objetos interactivos de aprendizaje, 31 de ellos diseñados con el editor DescartesJS. Para evitar, al máximo, la dependencia con la conectividad en la red, las expresiones matemáticas se han construido recurriendo al diseño de algunas clases en la hoja de estilos (style.css) y, en algunos casos, al editor DescartesJS. Se ha conservado la propuesta pedagógica en los ejemplos presentados en cada uno de los capítulos, los cuales incluyen: formulación del problema, estrategia de solución, solución, explicación o sentido de los resultados obtenidos y, en la mayoría de los ejemplos, un problema propuesto, denominado "Comprueba tu aprendizaje". Al final de cada capítulo se han incluido tanto los problemas propuestos como las respuestas.
Evaluaciones que refuerzan conceptos clave
Los ejemplos del capítulo generalmente siguen un formato de tres partes de Estrategia, Solución y Significado para enfatizar cómo abordar un problema, cómo trabajar con las ecuaciones y cómo verificar y generalizar el resultado. Los ejemplos son a menudo seguidos por las preguntas y respuestas de "Comprueba tu aprendizaje" para ayudar a reforzar a los estudiantes las ideas importantes de los ejemplos. Las estrategias de resolución de problemas en cada capítulo desglosan los métodos para abordar diversos tipos de problemas en pasos que los estudiantes pueden seguir para obtener orientación. El libro también incluye ejercicios al final de cada capítulo para que los estudiantes puedan practicar lo que aprendieron. Las preguntas conceptuales no requieren cálculos, pero evalúan el aprendizaje de los conceptos clave por parte del alumno. Los problemas clasificados por sección evalúan las habilidades de resolución de problemas del estudiante y la capacidad de aplicar ideas a la práctica.

El calor y la temperatura son conceptos importantes para cada uno de nosotros, todos los días. Cómo nos vestimos por la mañana depende de si el día está frío o caliente, y la mayoría de lo que hacemos requiere energía que en última instancia proviene del sol. El estudio del calor y la temperatura es parte de un área de la física conocida como termodinámica. Las leyes de la termodinámica rigen el flujo de energía en todo el universo. Se estudian en todas las áreas de la ciencia y la ingeniería, desde la química hasta la biología y la ciencia ambiental.
En este capítulo, exploraremos el calor y la temperatura. No siempre es fácil distinguir estos términos. El calor es el flujo de energía de un objeto a otro, que es causado por una diferencia de temperatura. La transferencia de calor puede cambiar la temperatura. Estas ideas básicas afectan todo, desde el comportamiento de los átomos y las moléculas hasta la cocina, nuestro clima en la Tierra y los ciclos de vida de las estrellas.
El calor es familiar para todos nosotros. Podemos sentir calor entrando en nuestros cuerpos desde el sol del verano o desde el café o el té caliente después de un paseo de invierno. También podemos sentir calor al dejar nuestros cuerpos sentir el frío de la noche o el efecto refrescante del sudor después del ejercicio.
¿Qué es calor? ¿Cómo lo definimos y cómo se relaciona con la temperatura? ¿Cuáles son los efectos del calor y cómo fluye de un lugar a otro? Encontraremos que, a pesar de la riqueza de los fenómenos, un pequeño conjunto de principios físicos subyacentes une estos temas y los vincula a otros campos. Comenzamos examinando la temperatura, cómo definirla y medirla.
El concepto de temperatura ha evolucionado a partir de los conceptos comunes de frío y calor. La definición científica de temperatura explica más que nuestros sentidos de frío y calor. Como ya habrás aprendido, muchas cantidades físicas se definen únicamente en términos de cómo se observan o se miden, es decir, se definen operacionalmente. La temperatura se define operativamente como la cantidad de lo que medimos con un termómetro.
Como veremos en detalle en el siguiente capítulo, la temperatura es proporcional a la energía cinética promedio de la traslación, un hecho que proporciona una definición más física. Las diferencias de temperatura mantienen la transferencia de calor en todo el universo. La transferencia de calor es el movimiento de energía de un lugar o material a otro como resultado de una diferencia de temperatura.
Un concepto importante relacionado con la temperatura es el equilibrio térmico. Dos objetos están en equilibrio térmico si están en contacto cercano que les permite obtener energía del otro, pero sin embargo, no se transfiere energía neta entre ellos. Incluso cuando no están en contacto, están en equilibrio térmico si, cuando se ponen en contacto, no se transfiere energía neta entre ellos. Si dos objetos permanecen en contacto durante un tiempo prolongado, normalmente llegan al equilibrio. En otras palabras, dos objetos en equilibrio térmico no intercambian energía.
Experimentalmente, si el objeto $A$ está en equilibrio con el objeto $B$, y el objeto $B$ está en equilibrio con el objeto $C$, entonces (como ya habrás adivinado) el objeto $A$ está en equilibrio con el objeto $C$. Esa declaración de transitividad se llama ley zeroth de la termodinámica (El número "zeroth" o "cero-ésimo" fue sugerido por el físico británico Ralph Fowler en la década de 1930. La primera, segunda y tercera leyes de la termodinámica ya estaban nombradas y numeradas. La ley zeroth rara vez se había establecido, pero debe discutirse antes de la otros, así que Fowler le dio un número más pequeño). Considera el caso donde $A$ es un termómetro. La ley zeroth nos dice que si $A$ lee cierta temperatura cuando está en equilibrio con $B$, y luego se pone en contacto con $C$, no intercambiará energía con $C$; por lo tanto, su lectura de temperatura seguirá siendo la misma (). En otras palabras, si dos objetos están en equilibrio térmico, tienen la misma temperatura.
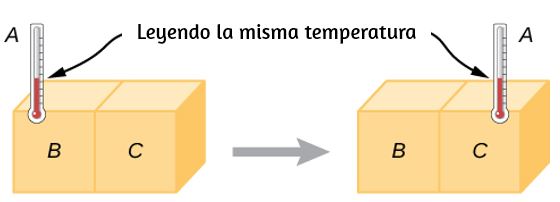
Un termómetro mide su propia temperatura. Es a través de los conceptos de equilibrio térmico y la ley zeroth de la termodinámica que podemos decir que un termómetro mide la temperatura de otra cosa y da sentido a la afirmación de que dos objetos están a la misma temperatura.
A menudo nos referiremos a "sistemas" en lugar de "objetos", pues un sistema consta de uno o más objetos, y en termodinámica necesitamos un sistema macroscópico, es decir, que consiste de un gran número (como $10^{23}$) de moléculas. Entonces podemos decir que un sistema está en equilibrio térmico consigo mismo si todas las partes de él están a la misma temperatura (Volveremos a la definición de un sistema termodinámico en el capítulo sobre la primera ley de la termodinámica).
Cualquier propiedad física que dependa de manera consistente y reproducible de la temperatura se puede utilizar como la base de un termómetro.
Por ejemplo, el volumen aumenta con la temperatura para la mayoría de las sustancias. Esta propiedad es la base para el termómetro de alcohol común y los termómetros originales de mercurio. Otras propiedades utilizadas para medir la temperatura incluyen la resistencia eléctrica, el color y la emisión de radiación infrarroja ().
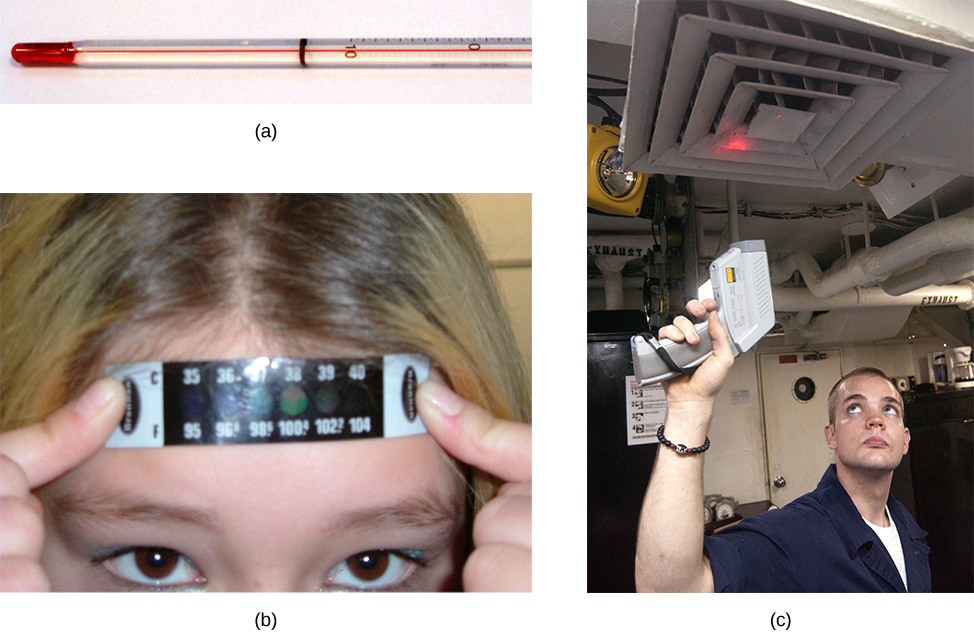
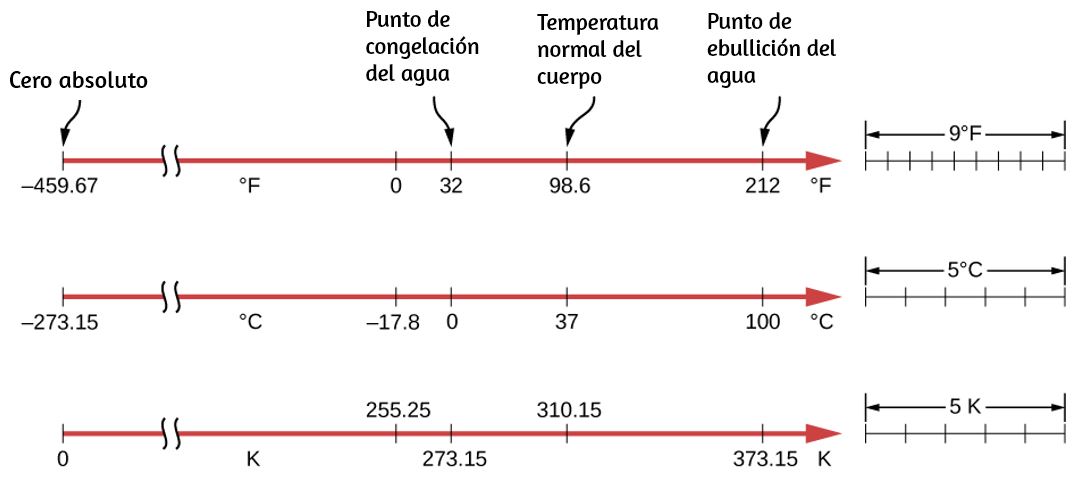
Los termómetros miden la temperatura de acuerdo con escalas de medición bien definidas. Las tres escalas de temperatura más comunes son Fahrenheit, Celsius y Kelvin. Las escalas de temperatura se crean identificando dos temperaturas reproducibles. Las temperaturas de congelación y ebullición del agua a presión atmosférica estándar se utilizan comúnmente.
En la escala Celsius, el punto de congelación del agua es de $0° C$ y el punto de ebullición es de $100 °C$. La unidad de temperatura en esta escala es el grado Celsius ($°C$). La escala Fahrenheit (aún la más utilizada con propósitos comunes en los Estados Unidos) tiene el punto de congelación del agua a $32 °F$ y el punto de ebullición a $212 °F$. Su unidad es el grado Fahrenheit ($°F$). Puedes ver que $100$ grados Celsius abarcan el mismo rango que $180$ grados Fahrenheit. Por lo tanto, una diferencia de temperatura de un grado en la escala Celsius es $1.8$ veces mayor que una diferencia de un grado en la escala Fahrenheit, o $ΔT_F = \frac{9}{5}ΔT_C$.
La definición de temperatura en términos de movimiento molecular sugiere que debería haber una temperatura más baja posible, donde la energía cinética promedio de las moléculas es cero (o el mínimo permitido por la mecánica cuántica). Los experimentos confirman la existencia de dicha temperatura, llamada cero absoluto. Una escala de temperatura absoluta es aquella cuyo punto cero es cero absoluto. Tales escalas son convenientes en la ciencia porque varias cantidades físicas, como el volumen de un gas ideal, están directamente relacionadas con la temperatura absoluta.
La escala Kelvin es la escala de temperatura absoluta que se usa comúnmente en la ciencia. La unidad de temperatura en el SI es el kelvin, que se abrevia $K$ (no va acompañado de un signo de grado).
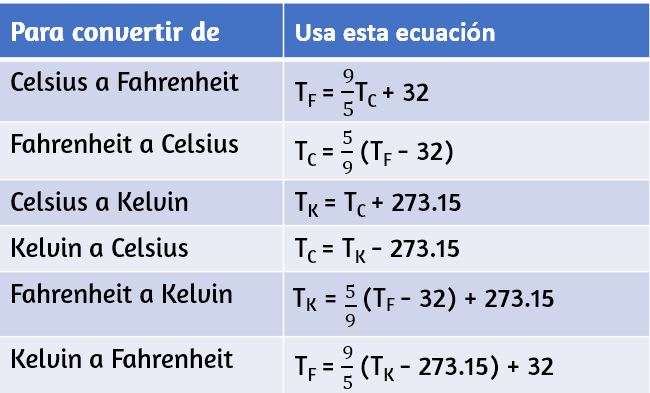
Por lo tanto $0 K$ es cero absoluto. Los puntos de congelación y ebullición del agua son $273.15 K$ y $373.15 K$, respectivamente. Por lo tanto, las diferencias de temperatura son las mismas en unidades de kelvins y grados Celsius, o $ΔT_C = ΔT_K$. Las relaciones entre las tres escalas de temperatura comunes se muestran en la . Las temperaturas en estas escalas se pueden convertir usando las ecuaciones en la .
Ejemplo 1.1
Conversión entre escalas de temperatura: temperatura ambiente
La "temperatura ambiente" que generalmente se define en física es de $25 °C$.
(a) ¿Cuál es la temperatura ambiente en $°F$?
(b) ¿Cuál es en $K$?
Estrategia
Para responder estas preguntas, todo lo que tenemos que hacer es elegir las ecuaciones de conversión correctas y sustituir los valores conocidos.
Solución
Para convertir de $°C$ a $°F$, usa la ecuación
$$T_F = \frac{9}{5}T_C + 32$$Sustituyendo:
$$T_F = \frac{9}{5}(25 °C) + 32 = 77 °F$$Del mismo modo, encontramos que
$$T_K = T_C + 273.15 = 298K$$Existen otras escalas. En la siguiente escena interactiva, diseñada por José Luis San Emeterio Peña, vemos la equivalencia entre la escala Celsius y las escalas Fahrenheit (de uso extendido en los países anglosajones) y Réaumur (casi en desuso).
La escala Kelvin es parte del sistema de unidades SI, por lo que su definición real es más complicada que la dada anteriormente. En primer lugar, no se define en términos de los puntos de congelación y ebullición del agua, sino en términos del punto triple. El punto triple es la combinación única de temperatura y presión a la que el hielo, el agua líquida y el vapor de agua pueden coexistir de manera estable. Como se discutirá en la sección sobre cambios de fase, la coexistencia se logra bajando la presión y, en consecuencia, el punto de ebullición para alcanzar el punto de congelación. La temperatura del punto triple se define como $273.16 K$. Esta definición tiene la ventaja de que, aunque la temperatura de congelación y la temperatura de ebullición del agua dependen de la presión, solo hay una temperatura de punto triple.
En segundo lugar, incluso con dos puntos en la escala definida, los diferentes termómetros dan resultados algo diferentes para otras temperaturas. Por lo tanto, se requiere un termómetro estándar. Los metrólogos (expertos en la ciencia de la medición) han elegido el termómetro de gas de volumen constante para este fin. Un recipiente de volumen constante lleno de gas se somete a cambios de temperatura, y la temperatura medida es proporcional al cambio de presión. Usando "$TP$" para representar el punto triple,
$$t = \frac{p}{p_{TP}}T_{TP}$$Los resultados dependen en cierta medida de la elección del gas, pero cuanto menos denso es el gas en el bulbo, mejores son los resultados para los diferentes gases. Si los resultados se extrapolan a densidad cero, los resultados coinciden bastante bien, con una presión cero correspondiente a una temperatura de cero absoluto. Los termómetros de gas de volumen constante son grandes y llegan al equilibrio lentamente, por lo que se usan principalmente como patrones para calibrar otros termómetros.
La expansión del alcohol en un termómetro es uno de los muchos ejemplos comúnmente encontrados de expansión térmica, que es el cambio en el tamaño o el volumen de un sistema dado, a medida que cambia la temperatura. El ejemplo más visible es la expansión del aire caliente. Cuando el aire se calienta, se expande y se vuelve menos denso que el aire circundante, que luego ejerce una fuerza (hacia arriba) sobre el aire caliente y eleva el vapor y el humo, los globos de aire caliente flotan. El mismo comportamiento ocurre en todos los líquidos y gases, impulsando la transferencia de calor natural hacia arriba en los hogares, los océanos y los sistemas meteorológicos, como veremos en una próxima sección. Los sólidos también experimentan expansión térmica. Las vías y puentes ferroviarios, por ejemplo, tienen juntas de expansión que les permiten expandirse y contraerse libremente con los cambios de temperatura, como se muestra en la .

¿Cuál es la causa subyacente de la expansión térmica? Como se mencionó anteriormente, un aumento en la temperatura significa un aumento en la energía cinética de los átomos individuales. En un sólido, a diferencia de un gas, las moléculas se mantienen en su lugar por las fuerzas de las moléculas vecinas. Las fuerzas se pueden modelar como en resortes armónicos descritos por el potencial de Lennard-Jones. La energía en el movimiento armónico simple muestra que tales potenciales son asimétricos en el sentido de que la energía potencial aumenta de forma más abrupta cuando las moléculas se acercan más que cuando se alejan. Por lo tanto, a una energía cinética determinada, la distancia recorrida es mayor cuando los vecinos se alejan unos de otros que cuando se mueven uno hacia el otro. El resultado es que el aumento de la energía cinética (aumento de la temperatura) aumenta la distancia promedio entre las moléculas: la sustancia se expande. Para la mayoría de las sustancias en condiciones normales, es una excelente aproximación que no hay una dirección preferida (es decir, el sólido es "isotrópico"), y un aumento de la temperatura aumenta el tamaño del sólido en una determinada fracción en cada dimensión. Por lo tanto, si el sólido es libre de expandirse o contraerse, sus proporciones se mantienen iguales; solo cambia su tamaño general.
En la siguiente escena interactiva, diseñada por Carlos Alberto Jaimes Vergara, podrás notar la diferencia de temperatura que se refleja en una diferencia en el movimiento de las moléculas y además, al mezclar dos sustancias con diferentes temperaturas, las moléculas de la sustancia con mayor temperatura empiezan a transferir su energía cinética a las moléculas de la sustancia con menor temperatura, debido a los choques que hay entre ellas. Para poder apreciar lo anterior, es necesario primero modificar las temperaturas de las dos secciones de la sustancia, es recomendable que la diferencia de temperatura entre ellas sea grande, así se puede notar de mejor manera lo ya expuesto, cuando estén listas las temperaturas entonces desplace la barrera a la derecha, utilice el botón con flecha verde mostrado en la imagen.
Nota que la barrera se mueve poco a poco a medida que presionas el botón, utiliza diferentes aberturas y observa que cuando es muy pequeña pero suficientemente grande para dejar que ciertas moléculas cambien de sección, el equilibrio térmico tardará en lograrse y que las moléculas con mayor rapidez tienen también mayor probabilidad de entrar a la sección con las moléculas de menor rapidez.
Expansión térmica lineal
Según los experimentos, la dependencia de la expansión térmica de la temperatura, la sustancia y la longitud original se resume en la ecuación
$$\frac{dL}{dT} = αL \tag{1.1}$$donde $ΔL$ es el cambio en la longitud $L$, $ΔT$ es el cambio en la temperatura, y $α$ es el coeficiente de expansión lineal, una propiedad del material que varía ligeramente con la temperatura. Como α es casi constante y también muy pequeño, para fines prácticos, usamos la aproximación lineal:
$$ΔL = αLΔT \tag{1.2}$$La enumera los valores representativos del coeficiente de expansión lineal. Como se señaló anteriormente, $ΔT$ es el mismo si se expresa en unidades de grados Celsius o kelvin; por lo tanto, α puede tener unidades de $1/°C$ o $1/K$ con el mismo valor en cualquier caso. La aproximación de $α$ como constante es bastante precisa para pequeños cambios de temperatura y suficiente para la mayoría de los fines prácticos, incluso para grandes cambios de temperatura. Examinamos esta aproximación más de cerca en el siguiente ejemplo.
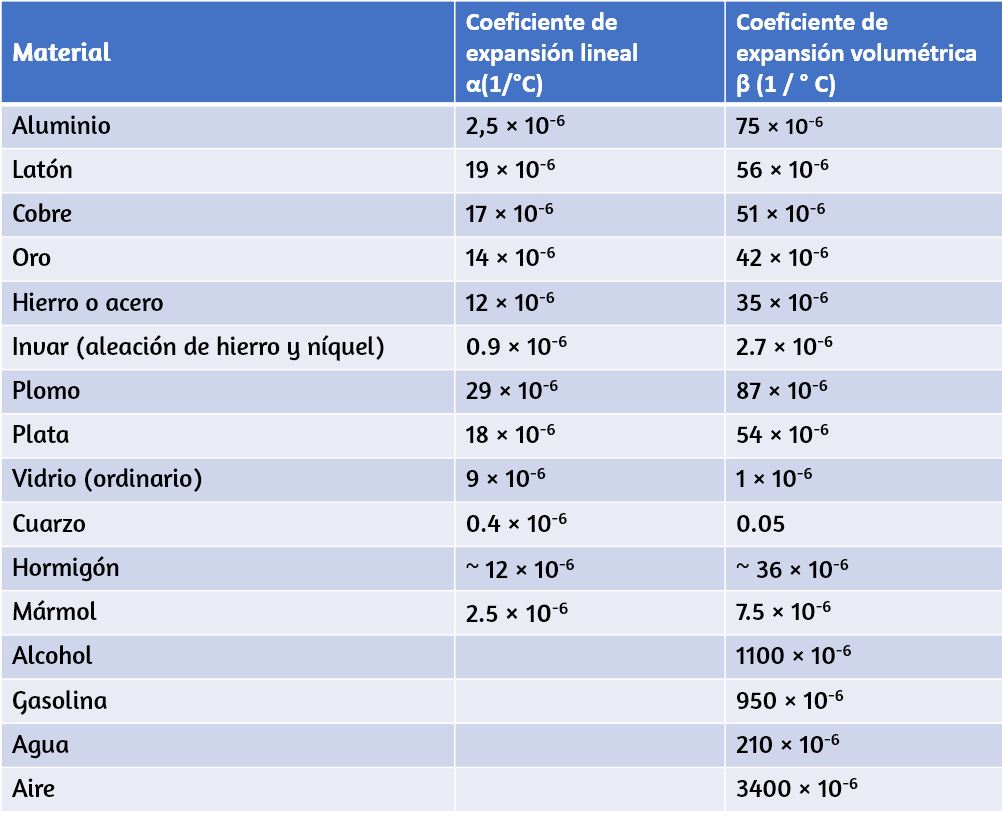
La expansión térmica se explota en la banda bimetálica (). Este dispositivo se puede usar como un termómetro si la banda curva está unida a un puntero en una escala. También se puede utilizar para cerrar o abrir automáticamente un interruptor a una temperatura determinada, como en termostatos antiguos o analógicos.
Ejemplo 1.2
Cálculo de la expansión térmica lineal
El tramo principal del Golden Gate Bridge de San Francisco tiene $1275 m$ de longitud en su punto más frío. El puente está expuesto a temperaturas que oscilan entre $-15 °C$ y $40 °C$. ¿Cuál es su cambio de longitud entre estas temperaturas? Supongamos que el puente está hecho completamente de acero.
Estrategia
Usa la ecuación para la expansión térmica lineal $ΔL = αLΔT$ para calcular el cambio en la longitud, $ΔL$. Utiliza el coeficiente de expansión lineal $α$ para el acero de la , y ten en cuenta que el cambio en la temperatura $ΔT$ es de $55 °C$.
Solución
Sustituye todos los valores conocidos en la ecuación para hallar $ΔL$:
$$ΔL = αLΔT = (12 × 10^{-6} °C) (1275 m) (55 °C) = 0.84m$$Explicación
Aunque no es grande en comparación con la longitud del puente, este cambio de longitud es observable. Generalmente se extiende sobre muchas juntas de expansión, por lo que la expansión en cada unión es pequeña.
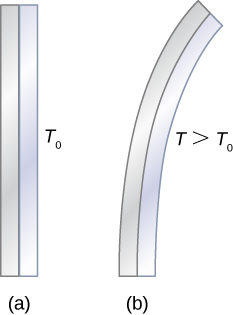
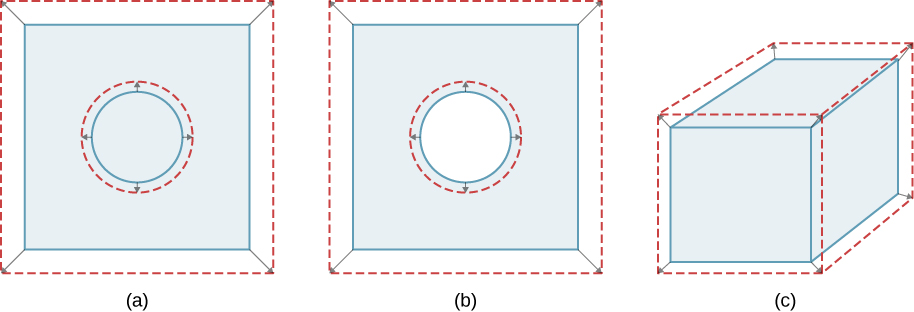
Los objetos no restringidos se expanden en todas las dimensiones, como se ilustra en la . Es decir, sus áreas y volúmenes, así como sus longitudes, aumentan con la temperatura. Debido a que las proporciones permanecen iguales, los agujeros y los volúmenes de los contenedores también aumentan con la temperatura. Si cortas un orificio en una placa de metal, el material restante se expandirá exactamente como lo haría si la pieza que retiras todavía estuviera en su lugar. La pieza se haría más grande, por lo que el agujero también debería agrandarse.
Expansión térmica en dos dimensiones
Para pequeños cambios de temperatura, el cambio en el área $ΔA$ viene dado por
$$ΔA = 2αAΔT \tag{1.3}$$donde $ΔA$ es el cambio en el área $A$, $ΔT$ es el cambio en la temperatura, y $α$ es el coeficiente de expansión lineal, que varía ligeramente con la temperatura (La derivación de esta ecuación es análoga a la de la ecuación más importante para tres dimensiones).
La expansión de volumen se define para los líquidos, pero la expansión lineal y de área no lo es, ya que los cambios de un líquido en las dimensiones lineales y el área dependen de la forma de su contenedor. Por lo tanto, la muestra los valores de los líquidos de $β$ pero no de $α$.
Expansión térmica en tres dimensiones
La relación entre el volumen y la temperatura $dV/dT$ está dada por $dV/dT = βVΔT$, donde $β$ es el coeficiente de expansión del volumen. Como puede mostrar en el ejercicio 1.60, $β = 3α$. Esta ecuación generalmente se escribe como
$$ΔV = βVΔT \tag{1.4}$$Tenga en cuenta que los valores de $β$ en la Tabla 1.2 son iguales a $3α$, excepto para el redondeo.
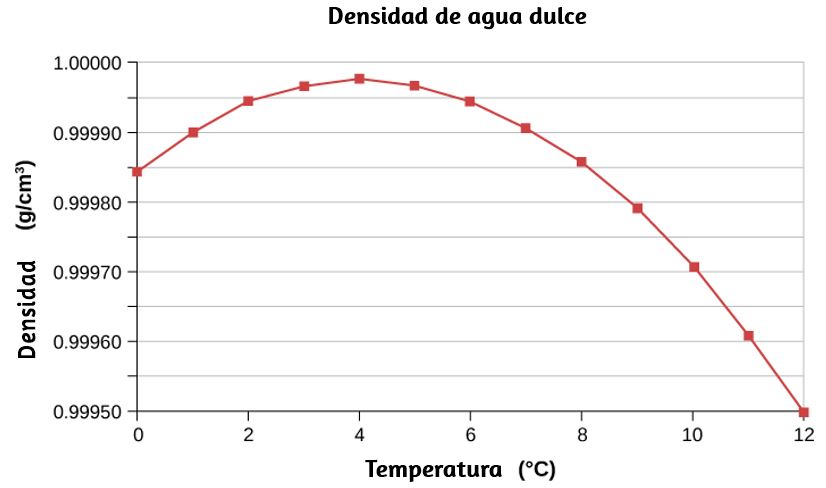
En general, los objetos se expanden al aumentar la temperatura. El agua es la excepción más importante a esta regla. El agua se expande al aumentar la temperatura (su densidad disminuye) a temperaturas superiores a $4 °C$ ($40 °F$). Sin embargo, es más denso a $+4 °C$ y se expande con una temperatura decreciente entre $+ 4 °C$ y $0 °C$ ($40 °F$ a $32 °F$), como se muestra en la . Un efecto sorprendente de este fenómeno es la congelación de agua en un estanque. Cuando el agua cerca de la superficie se enfría a $4 °C$, es más densa que el agua restante y, por lo tanto, se hunde hasta el fondo. Esta "renovación" deja una capa de agua más caliente cerca de la superficie, que luego se enfría. Sin embargo, si la temperatura en la capa de superficie cae por debajo de $4 °C$, esa agua es menos densa que el agua de abajo, y por lo tanto permanece cerca de la parte superior.
Como resultado, la superficie del estanque puede congelarse. La capa de hielo aísla el agua líquida debajo de ella de las bajas temperaturas del aire. Los peces y otras formas de vida acuática pueden sobrevivir en agua a $4 °C$ bajo el hielo, debido a esta característica inusual del agua.
Ejemplo 1.3
Cálculo de expansión térmica
Supón que tu tanque de gasolina de acero de $60.0 l$ ($15.9 gal$) está lleno de gas que está frío porque acaba de ser bombeado desde un depósito subterráneo. Ahora, tanto el tanque como la gasolina tienen una temperatura de $15.0 °C$. ¿Cuánta gasolina se ha derramado cuando se calientan a $35.0 °C$?
Estrategia
El tanque y la gasolina aumentan de volumen, pero la gasolina aumenta más, por lo que la cantidad derramada es la diferencia en sus cambios de volumen. Podemos usar la ecuación para la expansión de volumen para calcular el cambio en el volumen de la gasolina y del tanque (El tanque de gasolina puede tratarse como acero sólido).
Solución
Alternativamente, podemos combinar estas tres ecuaciones en una sola ecuación (ten en cuenta que los volúmenes originales son iguales).
$$\begin{align*} V_{\textsf{derramado}} &= (β_{\textsf{gas}} - β_s)VΔT \\ &= [(950 - 35) × 10^{-6} /°C](60.0L) (20.0 °C) = 1.10L \end{align*}$$Explicación
Esta cantidad es significativa, particularmente para un tanque de $60.0 l$.
El efecto es tan sorprendente porque la gasolina y el acero se expanden rápidamente. La tasa de cambio en las propiedades térmicas se analiza más adelante en este capítulo.
Si intentas tapar el tanque con fuerza para evitar el desbordamiento, encontrarás que de todos modos tiene fugas, ya sea alrededor del tapón o reventando el tanque. Estrechar fuertemente el gas en expansión es equivalente a comprimirlo, y tanto los líquidos como los sólidos resisten la compresión con fuerzas extremadamente grandes. Para evitar la ruptura de contenedores rígidos, estos contenedores tienen aberturas de aire, lo que les permite expandirse y contraerse sin tensarlos.
 Comprueba tu aprendizaje 1.1
Comprueba tu aprendizaje 1.1
Si cambias la temperatura de un objeto mientras evitas que se expanda o contraiga, el objeto estará sometido a un esfuerzo que es compresivo si el objeto se expande en ausencia de restricción y es extensible si se contrae. Este esfuerzo resultante de los cambios de temperatura se conoce como esfuerzo térmico. Puede ser bastante grande y puede causar daños.
Para evitar este esfuerzo, los ingenieros pueden diseñar componentes para que puedan expandirse y contraerse libremente.
Por ejemplo, en las carreteras, se dejan huecos deliberadamente entre los bloques para evitar que se desarrolle el esfuerzo térmico. Cuando no se pueden dejar huecos, los ingenieros deben considerar el esfuerzo térmico en sus diseños. Por lo tanto, las varillas de refuerzo en el concreto están hechas de acero porque el coeficiente de expansión lineal del acero es casi igual al del concreto.
Para calcular el esfuerzo térmico en una varilla cuyos extremos están fijados rígidamente, podemos pensar que la tensión se desarrolla en dos pasos. Primero, deja que los extremos se expandan (o contraigan) y encuentre la expansión (o contracción). Segundo, encuentra el esfuerzo necesario para comprimir (o extender) la varilla a su longitud original mediante los métodos que estudiaste en "Equilibrio estático y Elasticidad". En otras palabras, el $ΔL$ de la expansión térmica es igual al $ΔL$ de la distorsión elástica (excepto que los signos son opuestos).
Ejemplo 1.4
Cálculo del esfuerzo térmico
Los bloques de concreto están dispuestos uno al lado del otro en una carretera sin ningún espacio entre ellos, por lo que no pueden expandirse. El equipo de construcción hizo el trabajo en un día de invierno cuando la temperatura era de $5 °C$. Encuentra el esfuerzo en los bloques en un día caluroso de verano cuando la temperatura es de $38° C$. El módulo de Young de compresión del hormigón es $Y = 20 × 10^9 N/m^2$.
Estrategia
El esfuerzo $F/A$ viene dado por
$$\frac{F}{A} = Y\frac{αL_0ΔT}{L_0} = YαΔT,$$y como esperábamos, $L_0$ se cancela y $A$ aparece solo en $F/A$, la notación para la cantidad que estamos calculando. Ahora, solo necesitamos reemplazar:
$$\begin{align*} \frac{F}{A} &= (20 × 10^9 N/m^2)(12 × 10^{-6}/°C)(38 °C − 5 °C) \\ &= 7.9 × 10^6 N/m^2 \end{align*}$$Explicación
La resistencia a la compresión máxima del hormigón es de $20 × 10^6 N / m^2$, por lo que es poco probable que se rompan los bloques. Sin embargo, la resistencia máxima a la cizalladura del hormigón es de solo $2 × 10^6 N/m^2$, por lo que algunos podrían astillarse.
 Comprueba tu aprendizaje 1.2
Comprueba tu aprendizaje 1.2
Hemos visto en capítulos anteriores que la energía es uno de los conceptos fundamentales de la física. El calor es un tipo de transferencia de energía causada por una diferencia de temperatura y puede cambiar la temperatura de un objeto.
Como aprendimos anteriormente en este capítulo, la transferencia de calor es el movimiento de la energía de un lugar o material a otro como resultado de una diferencia de temperatura. La transferencia de calor es fundamental para actividades cotidianas como la calefacción y la cocina domésticas, así como para muchos procesos industriales. También forma una base para los temas en el resto de este capítulo.
También presentamos el concepto de energía interna, que se puede aumentar o disminuir mediante la transferencia de calor. Discutimos otra forma de cambiar la energía interna de un sistema, es decir, trabajar en él. Por lo tanto, estamos comenzando el estudio de la relación del calor y el trabajo, que es la base de los motores y refrigeradores y el tema central (y el origen del nombre) de la termodinámica.
Un sistema térmico tiene energía interna (también llamada energía térmica), que es la suma de las energías mecánicas de sus moléculas. La energía interna de un sistema es proporcional a su temperatura. Como vimos anteriormente en este capítulo, si dos objetos a diferentes temperaturas entran en contacto entre sí, la energía se transfiere del objeto más caliente al más frío hasta que los cuerpos alcanzan el equilibrio térmico (es decir, están a la misma temperatura). Ningún objeto es hecho por ninguno de los objetos porque ninguna fuerza actúa a distancia (como discutimos en Trabajo y Energía cinética).
Estas observaciones revelan que el calor es energía transferida espontáneamente debido a una diferencia de temperatura. La muestra un ejemplo de transferencia de calor.
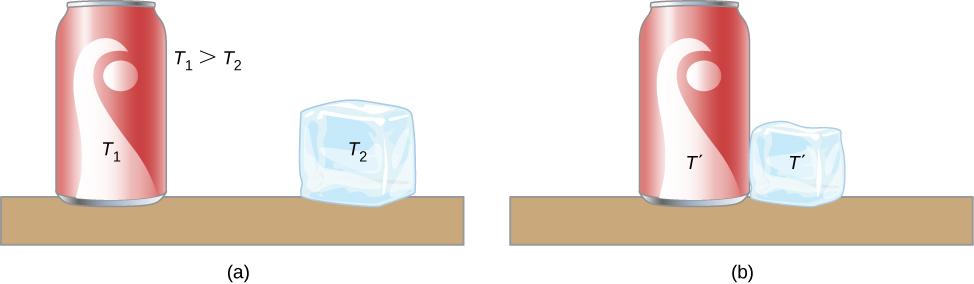
El significado de "calor" en física es diferente de su significado ordinario. Por ejemplo, en una conversación, podemos decir "el calor era insoportable", pero en física, diríamos que la temperatura era alta. El calor es una forma de flujo de energía, mientras que la temperatura no lo es. Por cierto, los humanos somos más sensibles al flujo de calor que a la temperatura.
Como el calor es una forma de energía, su unidad en el SI es el joule $(J)$. Otra unidad común de energía utilizada a menudo para el calor es la caloría ($cal$), definida como la energía necesaria para cambiar la temperatura de $1.00 g$ de agua por $1.00 °C$, específicamente, entre $14.5 °C$ y $15.5 °C$, ya que hay una ligera dependencia de la temperatura.
También es común el uso de la kilocaloría ($kcal$), que es la energía necesaria para cambiar la temperatura de $1.00 kg$ de agua por $1.00 °C$. Como la masa se especifica con mayor frecuencia en kilogramos, la kilocaloría es conveniente. Confusamente, las calorías de los alimentos (abreviadas $Cal$) son en realidad kilocalorías, un hecho que no se determina fácilmente a partir del etiquetado del paquete.
También es posible cambiar la temperatura de una sustancia haciendo trabajo, que transfiere energía hacia o desde un sistema. Esta comprensión ayudó a establecer que el calor es una forma de energía. James Prescott Joule (1818-1889) realizó muchos experimentos para establecer el equivalente mecánico del calor, el trabajo necesario para producir los mismos efectos que la transferencia de calor. En las unidades utilizadas para estas dos cantidades, el valor de esta equivalencia es
$$1,000 kcal = 4186 J$$Consideramos que esta ecuación representa la conversión entre dos unidades de energía (Otros números que puedes ver se refieren a calorías definidas para rangos de temperatura que no sean de $14.5 °C$ a $15.5 °C$).
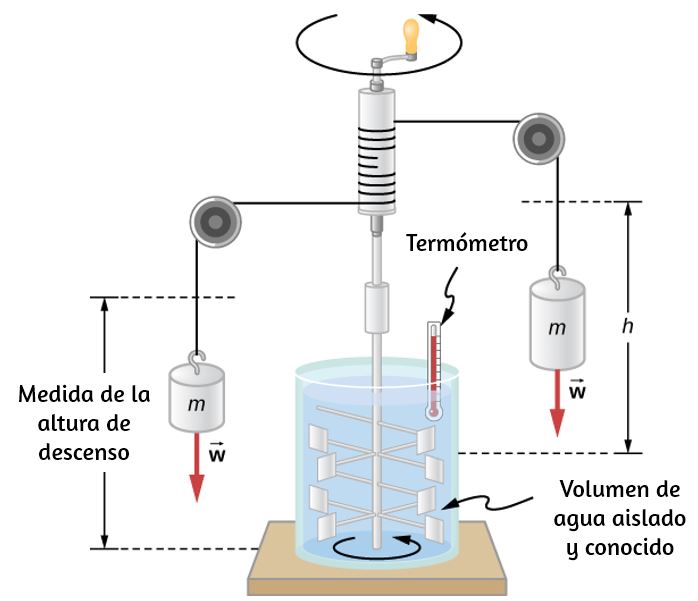
La muestra una de las configuraciones experimentales más famosas de Joule para demostrar que el trabajo y el calor pueden producir los mismos efectos y medir el equivalente mecánico del calor. Ayudó a establecer el principio de la conservación de la energía. La energía potencial gravitacional ($U$) se convirtió en energía cinética ($K$), y luego se aleatorizó mediante la viscosidad y la turbulencia en un aumento de la energía cinética media de los átomos y moléculas en el sistema, produciendo un aumento de la temperatura.
Las contribuciones de Joule a la termodinámica fueron tan significativas que la unidad de energía en el SI recibió su nombre.
El aumento de la energía interna por transferencia de calor da el mismo resultado que aumentarlo haciendo el trabajo. Por lo tanto, aunque un sistema tiene una energía interna bien definida, no podemos decir que tiene un cierto "contenido de calor" o "contenido de trabajo". Una cantidad bien definida que depende únicamente del estado actual del sistema, en lugar de la historia de ese sistema, se conoce como una variable de estado. La temperatura y la energía interna son variables de estado. Para resumir este párrafo, el calor y el trabajo no son variables de estado.
Incidentalmente, aumentar la energía interna de un sistema no necesariamente aumenta su temperatura. Como veremos en la siguiente sección, la temperatura no cambia cuando una sustancia cambia de una fase a otra. Un ejemplo es la fusión del hielo, que se puede lograr mediante la adición de calor o haciendo un trabajo de fricción, como cuando un cubo de hielo se frota contra una superficie rugosa.
Hemos notado que la transferencia de calor a menudo causa un cambio de temperatura. Los experimentos muestran que sin cambio de fase y sin trabajo realizado en o por el sistema, el calor transferido es típicamente directamente proporcional al cambio de temperatura y a la masa del sistema, en una buena aproximación (A continuación mostramos cómo manejar situaciones en las que la aproximación no es válida). La constante de proporcionalidad depende de la sustancia y su fase, que puede ser gaseosa, líquida o sólida. Omitimos la discusión de la cuarta fase, plasma, porque aunque es la fase más común en el universo, es rara y de corta duración en la Tierra.
Podemos entender los hechos experimentales al notar que el calor transferido es el cambio en la energía interna, que es la energía total de las moléculas. La energía cinética promedio de una molécula $K_{\textsf{prom}}$ es proporcional a la temperatura absoluta. Por lo tanto, el cambio en la energía interna de un sistema es proporcional al cambio de temperatura y al número de moléculas, $N$. Matemáticamente, $ΔU α ΔK_{\textsf{total}} = NK_{\textsf{prom}} α NΔT$. La dependencia de la sustancia resulta en gran parte de las diferentes masas de átomos y moléculas. Estamos considerando su capacidad de calor en términos de su masa pero, en algunos casos, las capacidades de calor por molécula son similares para diferentes sustancias. La dependencia de la sustancia y la fase también resulta de las diferencias en la energía potencial asociada con las interacciones entre átomos y moléculas.
Cambio de calor y cambio de temperatura
Una aproximación práctica para la relación entre la transferencia de calor y el cambio de temperatura es:
$$Q = mcΔT \tag{1.5}$$donde $Q$ es el símbolo de la transferencia de calor ("cantidad de calor"), $m$ es la masa de la sustancia y $ΔT$ es el cambio de temperatura. El símbolo $c$ representa el calor específico (también llamado "capacidad calorífica específica") y depende del material y la fase. El calor específico es numéricamente igual a la cantidad de calor necesaria para cambiar la temperatura de $1.00 kg$ de masa por $1.00 °C$. La unidad SI para calor específico es $J/(kg × K)$ o $J/(kg × °C)$. (Recuerda que el cambio de temperatura $ΔT$ es el mismo en unidades de Kelvin y grados Celsius).
En la siguiente escena interactiva, diseñada por Mario Belloni, Wolfgang Christian y Anne J Cox, una masa azul se encuentra en un horno aislado.
Supón que el bloque absorbe todo el calor del calentador (el tiempo se da en minutos y la temperatura en grados Celsius). No es sorprendente que un calentador de mayor potencia (la cantidad de calor entregado/segundo) resulte en una temperatura más alta de la masa azul durante el mismo intervalo de tiempo. Ten en cuenta que a medida que cambia la masa del objeto, el cambio de temperatura es diferente (para una potencia dada del horno). La descripción cuantitativa de esto viene dada por la ecuación $Q = mc(T_f - T_i)$.
Ten en cuenta que si duplicas la masa, para el mismo calor total entregado, el cambio de temperatura se reducirá a la mitad.
Los valores de calor específico generalmente se deben medir, porque no hay una manera simple de calcularlos con precisión. La enumera valores representativos de calor específico para diversas sustancias. Vemos en esta tabla que el calor específico del agua es cinco veces mayor que el del vidrio y 10 veces más que el hierro, lo que significa que se requiere cinco veces más calor para elevar la temperatura del agua una cantidad determinada que para el vidrio. De hecho, el agua tiene uno de los calores específicos más grandes de cualquier material, lo cual es importante para mantener la vida en la Tierra. Los calores específicos de gases dependen de lo que se mantiene constante durante el calentamiento, típicamente el volumen o la presión. En la tabla, el primer valor de calor específico para cada gas se mide a volumen constante, y el segundo (entre paréntesis) se mide a presión constante.
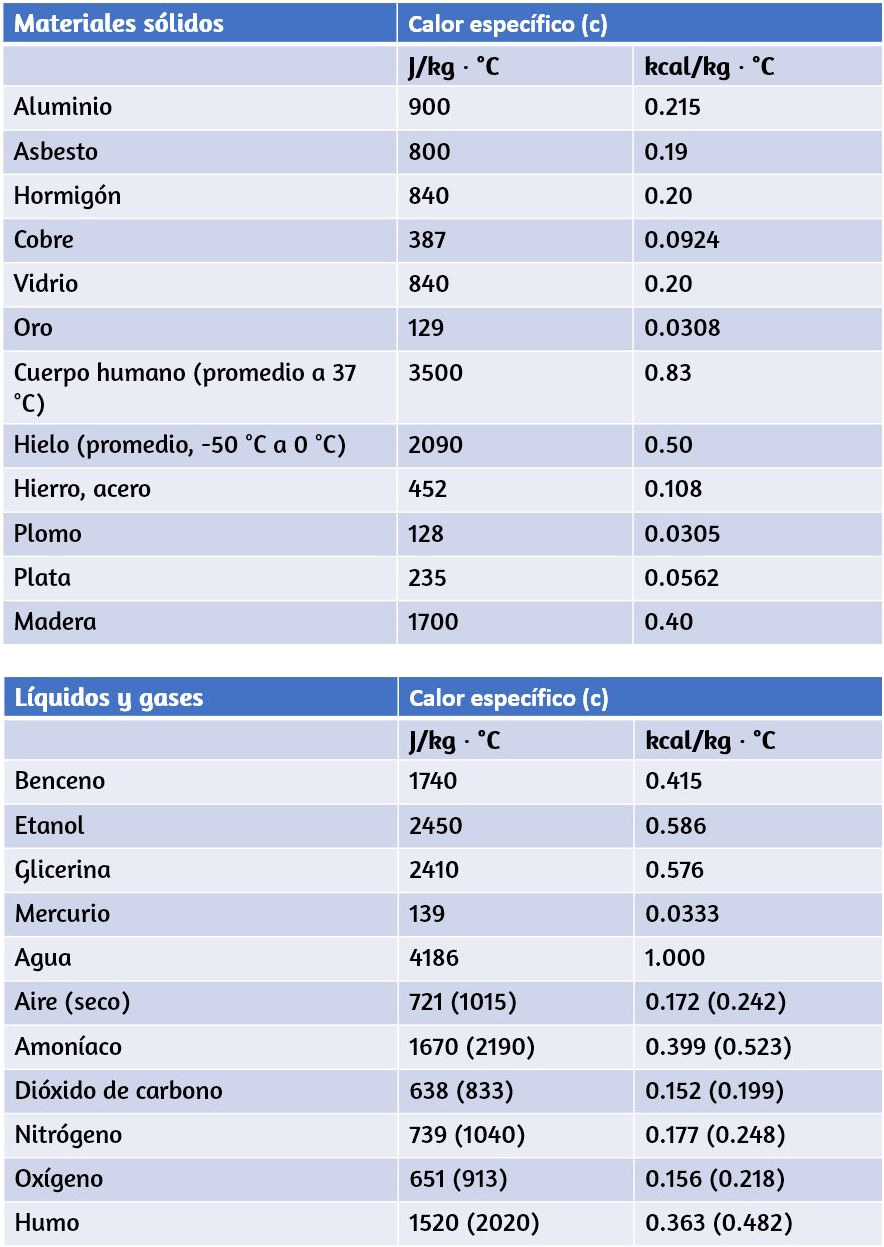
En general, el calor específico también depende de la temperatura. Por lo tanto, debe darse una definición precisa de c para una sustancia en términos de un cambio infinitesimal en la temperatura. Para hacer esto, notamos que $c = \frac{1}{m}\frac{ΔQ}{ΔT}$, reemplazando $Δ$ por $d$:
$$c = \frac{1}{m}\frac{dQ}{dT}$$A excepción de los gases, la dependencia de la temperatura y el volumen del calor específico de la mayoría de las sustancias es débil a temperaturas normales.
Por lo tanto, generalmente tomaremos calores específicos como constantes, según los valores dados en la tabla.
Ejemplo 1.5
Cálculo del calor requerido
Una bandeja de aluminio de $0.500 kg$ en una estufa y $0.250 L$ de agua en ella se calienta de $20.0 °C$ a $80.0 °C$. (a) ¿Cuánto calor se requiere? ¿Qué porcentaje del calor se usa para elevar la temperatura de (b) la bandeja y (c) el agua?
Estrategia
Podemos suponer que la sartén y el agua están siempre a la misma temperatura. Cuando colocas la sartén sobre la estufa, la temperatura del agua y la de la sartén aumentan en la misma cantidad. Usamos la ecuación para la transferencia de calor para el cambio de temperatura y la masa de agua y aluminio dados. Los valores de calor específicos para agua y aluminio se dan en la .
Solución
1. Calcula la diferencia de temperatura: $ΔT = T_f − T_i = 60.0 °C$
2. Calcula la masa de agua. Debido a que la densidad del agua es de $1000 kg/m^3$, $1 L$ de agua tiene una masa de $1 kg$, y la masa de $0.250 L$ de agua es $m_w = 0.250 kg$.
3. Calcula el calor transferido al agua. Usa el calor específico del agua en la :
$$Q_w = m_wc_wΔT = (0.250 kg)(4186 J/kg °C)(60.0 °C) = 62.8 kJ$$4. Calcula el calor transferido al aluminio. Use el calor específico para aluminio en la :
$$Q_{\textsf{Al}} = m_{\textsf{Al}}c_{\textsf{Al}}ΔT = (0.500 kg)(900 J/kg °C)(60.0 °C) = 27.0 kJ$$5. Encuentra el calor transferido total:
$$Q_{\textsf{total}} = Q_w + Q_{\textsf{Al}} = 89.8 kJ$$Explicación
En este ejemplo, el calor transferido al contenedor es una fracción significativa del calor total transferido. Aunque la masa de la sartén es el doble que la del agua, el calor específico del agua es más de cuatro veces mayor que el del aluminio. Por lo tanto, se necesita un poco más de dos veces más calor para lograr el cambio de temperatura dado para el agua y para la bandeja de aluminio.
El ejemplo 1.6 ilustra un aumento de temperatura causado por el trabajo (El resultado es el mismo que si se hubiera agregado la misma cantidad de energía con un soplete en vez de mecánicamente).
Ejemplo 1.6
Cálculo del aumento de temperatura del trabajo realizado en una sustancia
Los frenos de los camiones utilizados para controlar la velocidad en una carrera cuesta abajo funcionan, convirtiendo la energía potencial gravitacional en una mayor energía interna (temperatura más alta) del material de los frenos (). Esta conversión evita que la energía potencial gravitacional se convierta en energía cinética del camión. Como la masa del camión es mucho mayor que la del material de freno que absorbe la energía, el aumento de la temperatura puede ocurrir demasiado rápido para que pase suficiente calor desde los frenos al medio ambiente; en otras palabras, los frenos pueden sobrecalentarse.

Calcula el aumento de temperatura de 10 kg de material de freno con un calor específico promedio de $800 J/kg \cdot °C$ si el material retiene el $10$% de la energía de un camión de $10,000 kg$ que desciende $75.0 m$ a velocidad constante.
Estrategia
Calculamos la energía potencial gravitacional ($Mgh$) que todo el camión pierde en su descenso, lo equiparamos con el aumento en la energía interna de los frenos, y luego encontramos el aumento de temperatura producido solo en el material del freno.
Solución
Primero calculamos el cambio en la energía potencial gravitatoria a medida que el camión va cuesta abajo:
$$Mgh = (10,000 kg)(9.80 m/s^2)(75.0 m) = 7.35 × 10^6 J$$Debido a que la energía cinética del camión no cambia, la conservación de la energía nos dice que la energía potencial perdida se disipa, y suponemos que el $10$% de ella se transfiere a la energía interna de los frenos, por lo tanto, toma $Q = Mgh/10$. Luego calculamos el cambio de temperatura del calor transferido, usando
$$ΔT = \frac{Q}{mc}$$donde m es la masa del material de freno. reemplaza los valores dados para encontrar:
$$ΔT = \frac{7.35 × 10^5 J}{(10 kg)(800 J/kg°C)} = 92 °C$$Explicación
Si el camión había estado viajando durante algún tiempo, justo antes del descenso, la temperatura del freno probablemente sería más alta que la temperatura ambiente.
El aumento de temperatura en el descenso probablemente elevaría la temperatura del material de freno muy alta, por lo que esta técnica no es práctica. En cambio, el camión usaría la técnica del frenado del motor. Una idea diferente subyace en la tecnología reciente de los automóviles híbridos y eléctricos, donde la energía mecánica (energía potencial cinética y gravitatoria) se convierte por los frenos en energía eléctrica en la batería, un proceso llamado frenado regenerativo.
En un tipo común de problema, los objetos a diferentes temperaturas se ponen en contacto entre sí pero aislados de todo lo demás, y se les permite llegar al equilibrio. Un contenedor que previene o no la transferencia de calor se llama calorímetro, y el uso de un calorímetro para realizar mediciones (generalmente de calor o capacidad de calor específico) se denomina calorimetría. Usaremos el término "problema de calorimetría" para referirnos a cualquier problema en el que los objetos en cuestión estén aislados térmicamente de su entorno. Una idea importante para resolver problemas de calorimetría es que durante la transferencia de calor entre objetos aislados de su entorno, el calor obtenido por el objeto más frío debe ser igual al calor perdido por el objeto más caliente, debido a la conservación de la energía:
Expresamos esta idea al escribir que la suma de los calores es igual a cero porque el calor ganado generalmente se considera positivo; el calor perdido, negativo.
Ejemplo 1.7
Cálculo de la temperatura final en calorimetría
Supón que viertes $0.250 kg$ de agua a $20.0 °C$ (aproximadamente una taza) en una bandeja de aluminio de $0.500 kg$ fuera de la estufa a una temperatura de $150 °C$. Supón que no se produce ninguna transferencia de calor a otra cosa: la bandeja se coloca en una almohadilla aislada, y la transferencia de calor al aire se desprecia en el corto tiempo necesario para alcanzar el equilibrio. Por lo tanto, este es un problema de calorimetría, aunque no se especifica ningún contenedor de aislamiento. También asume que una cantidad despreciable de agua hierve. ¿Cuál es la temperatura cuando el agua y la sartén alcanzan el equilibrio térmico?
Estrategia
Originalmente, la bandeja y el agua no están en equilibrio térmico: la bandeja está a una temperatura más alta que el agua. La transferencia de calor restablece el equilibrio térmico una vez que el agua y el recipiente están en contacto; se detiene una vez que se logra el equilibrio térmico entre la bandeja y el agua. El calor perdido por la sartén es igual al calor ganado por el agua, ese es el principio básico de la calorimetría.
Solución
1. Usa la ecuación para transferencia de calor $Q = mcΔT$ para expresar el calor perdido por la bandeja de aluminio en términos de la masa de la bandeja, el calor específico del aluminio, la temperatura inicial de la bandeja y la temperatura final:
$$Q_{\textsf{caliente}} = m_{A1}c_{A1}(T_f − 150 °C)$$2. Expresa el calor ganado por el agua en términos de la masa de agua, el calor específico del agua, la temperatura inicial del agua y la temperatura final:
$$Q_{\textsf{frío}} = m_wc_w(T_f - 20.0 °C)$$3. Ten en cuenta que $Q_{\textsf{caliente}} < 0$ y $Q_{\textsf{frío}} > 0$ y, que como se indicó anteriormente, deben sumar a cero:
$$Q_{\textsf{frío}} + Q_{\textsf{caliente}} = 0$$ $$Q_{\textsf{frío}} = -Q_{\textsf{caliente}}$$ $$m_wc_w(T_f - 20.0 °C) = -m_{A1}c_{A1}(T_f − 150 °C)$$4. Esta es una ecuación lineal para la temperatura final, $T_f$. Resolviendo para $T_f$,
$$T_f = \frac{m_{A1}c_{A1}(150 °C) + m_wc_w(20.0 °C)}{m_{A1}c_{A1} + m_wc_w}$$e inserta los valores numéricos:
Explicación
¿Por qué la temperatura final está mucho más cerca de $20.0 °C$ que a $150 °C$? La razón es que el agua tiene un calor específico mayor que la mayoría de las sustancias comunes y, por lo tanto, sufre un cambio de temperatura menor para una transferencia de calor determinada. Un gran cuerpo de agua, como un lago, requiere una gran cantidad de calor para aumentar su temperatura de manera apreciable. Esto explica por qué la temperatura de un lago se mantiene relativamente constante durante el día, incluso cuando el cambio de temperatura del aire es grande. Sin embargo, la temperatura del agua cambia en tiempos más largos (por ejemplo, de verano a invierno).
 Comprueba tu aprendizaje 1.3
Comprueba tu aprendizaje 1.3
Ejemplo 1.8
Capacidad de calor dependiente de la temperatura
A bajas temperaturas, los calores específicos de sólidos son típicamente proporcionales a $T^3$. La primera comprensión de este comportamiento se debió al físico holandés Peter Debye, quien en 1912, trató las oscilaciones atómicas con la teoría cuántica que Max Planck había utilizado recientemente para la radiación.
Por ejemplo, una buena aproximación para el calor específico de la sal, $NaCl$, es $c = 3.33 × 10^4 \frac{J}{kg \cdot k}(\frac{T}{321K})^3$. La constante $321K$ se llama la temperatura de Debye de $NaCl$, $Θ_D$, y la fórmula funciona bien cuando $T < 0.04Θ_D$. Usando esta fórmula, ¿cuánto calor se requiere para elevar la temperatura de $24.0 g$ de $NaCl$ de $5 K$ a $15 K$?
Solución
Debido a que la capacidad de calor depende de la temperatura, necesitamos usar la ecuación
$$c = \frac{1}{m}\frac{dQ}{dT}$$Resolvemos esta ecuación para $Q$ integrando ambos lados:
$$Q = m \int_{T_1}^{T_2} cdT$$Luego sustituimos los valores dados y evaluamos la integral:
$$\begin{align*} Q &= (0.024 kg) \int_{T_1}^{T_2} 333 × 10^4\frac{J}{kg \cdot K}\left(\frac{T}{321K} \right)^3dT \\ &= \left(6.04 × 10^{-4}\frac{J}{K^4} \right)T^4 \Bigg|_{5K}^{15K} = 30.2 J \end{align*}$$Explicación
Si hubiéramos utilizado la ecuación $Q = mcΔT$ y el calor específico de la sal a temperatura ambiente, $880 J/kg \cdot K$, habríamos obtenido un valor muy diferente.
Las transiciones de fase desempeñan un importante papel teórico y práctico en el estudio del flujo de calor. En la fundición (o "fusión"), un sólido se convierte en líquido; el proceso opuesto es congelante. En la evaporación, un líquido se convierte en un gas; el proceso opuesto es condensación.
Una sustancia se derrite o se congela a una temperatura llamada su punto de fusión, y hierve (se evapora rápidamente) o se condensa en su punto de ebullición. Estas temperaturas dependen de la presión. La alta presión favorece la forma más densa, por lo que típicamente, la alta presión aumenta el punto de fusión y el punto de ebullición, y la baja presión los reduce. Por ejemplo, el punto de ebullición del agua es $100 °C$ a $1.00 atm$. A una presión más alta, el punto de ebullición es más alto, y a una presión más baja, es más bajo.
La fase de una sustancia dada depende de la presión y la temperatura. Por lo tanto, las gráficas de presión frente a la temperatura que muestran la fase en cada región proporcionan una visión considerable de las propiedades térmicas de las sustancias. Tal gráfico $pT$ se llama diagrama de fase.
La muestra el diagrama de fase para el agua. Usando el gráfico, si conoces la presión y la temperatura, puedes determinar la fase del agua. Las curvas sólidas (límites entre fases) indican transiciones de fase, es decir, temperaturas y presiones a las que coexisten las fases. Por ejemplo, el punto de ebullición del agua es $100 °C$ a $1.00 atm$. A medida que aumenta la presión, la temperatura de ebullición aumenta gradualmente a $374 °C$ a una presión de $218 atm$.
Una olla a presión (o incluso una olla tapada) cocina los alimentos más rápido que una olla abierta, porque el agua puede existir como un líquido a temperaturas superiores a $100 °C$ sin que todo hierva (Como veremos en la siguiente sección, el agua líquida conduce el calor mejor que el vapor o el aire caliente).
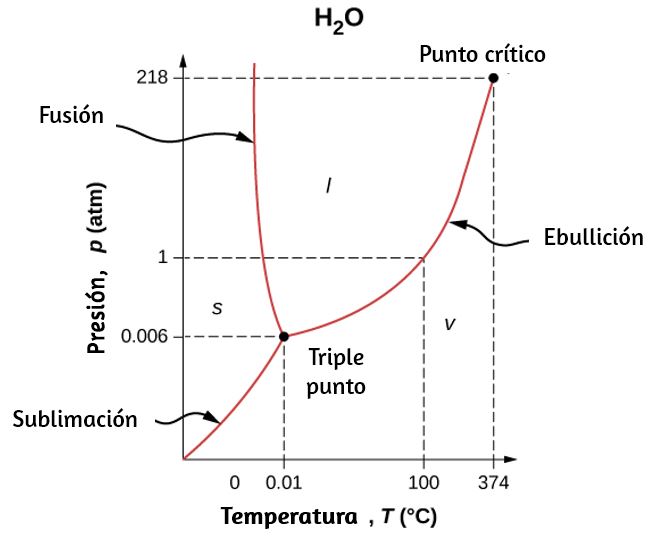
La curva del punto de ebullición finaliza en un punto llamado punto crítico, es decir, una temperatura crítica, por encima de la cual en el líquido y en el gas las fases no se pueden distinguir; la sustancia se llama fluido supercrítico.
A una presión suficientemente alta por encima del punto crítico, el gas tiene la densidad de un líquido pero no se condensa. El dióxido de carbono, por ejemplo, es supercrítico a todas las temperaturas superiores a $31,0 °C$. La presión crítica es la presión del punto crítico.
De manera similar, la curva entre las regiones sólida y líquida de la proporciona la temperatura de fusión a varias presiones. Por ejemplo, el punto de fusión es $0 °C$ a $1.00 atm$, como se esperaba. El agua tiene la propiedad inusual de que el hielo es menos denso que el agua líquida en el punto de fusión, por lo que a una temperatura fija, puede cambiar la fase de sólido (hielo) a líquido (agua) aumentando la presión. Es decir, la temperatura de fusión del hielo disminuye al aumentar la presión, como lo muestra el diagrama de fases. Por ejemplo, cuando un automóvil se conduce sobre la nieve, la mayor presión de los neumáticos derrite los copos de nieve; luego, el agua se vuelve a congelar y forma una capa de hielo.
Como aprendiste en la sección anterior sobre termómetros y escalas de temperatura, el punto triple es la combinación de temperatura y presión a la que el hielo, el agua líquida y el vapor de agua pueden coexistir de manera estable, es decir, las tres fases existen en equilibrio. Para el agua, el punto triple ocurre a $273.16 K$ ($0.01 °C$) y $611.2 Pa$; esa es una temperatura de calibración más precisa que el punto de fusión del agua a $1.00 atm$, o $273.15 K$ ($0.0 °C$).
En el siguiente objeto interactivo de PhET Simulaciones Calienta, enfría y comprime los átomos y las moléculas y observa cómo cambian entre sólido, líquido y fases gaseosas.
El objeto interactivo: Describe las características de los tres estados de la materia: sólido, líquido y gaseoso; Predice cómo al variar la temperatura o la presión cambia el comportamiento de las partículas; Compara las partículas en las tres fases diferentes.
Explica, además, la congelación y la fusión con detalle a nivel molecular. Reconoce que las sustancias diferentes tienen propiedades diferentes, incluyendo la temperatura de fusión, congelación y ebullición.
A presiones inferiores a la del punto triple, no hay fase líquida; la sustancia puede existir como gas o sólido. Para el agua, no hay fase líquida a presiones por debajo de $0.00600 atm$. El cambio de fase de sólido a gas se llama sublimación. Es posible que hayas notado que la nieve puede desaparecer en el aire sin un rastro de agua líquida, o que los cubitos de hielo pueden desaparecer en un congelador. Ambos son ejemplos de sublimación. También ocurre lo contrario: la escarcha se puede formar en ventanas muy frías sin pasar por la fase líquida. La muestra el resultado, así como también muestra un ejemplo familiar de sublimación. El dióxido de carbono no tiene fase líquida a la presión atmosférica.

El $CO_2$ sólido se conoce como hielo seco porque en lugar de derretirse, sublima. Su temperatura de sublimación a presión atmosférica es $-78 °C$. Ciertos ambientadores utilizan la sublimación de un sólido para esparcir un perfume por la habitación. Algunos sólidos, como el tetróxido de osmio, son tan tóxicos que deben guardarse en contenedores sellados para evitar la exposición humana a los vapores producidos por la sublimación.
A la temperatura de fusión, las fases sólida y líquida están en equilibrio. Si se agrega calor, parte del sólido se derretirá, y si se elimina el calor, parte del líquido se congelará. La situación es algo más compleja para el equilibrio líquido-gas. En general, el líquido y el gas están en equilibrio a cualquier temperatura. Llamamos vapor a la fase gaseosa cuando existe a una temperatura inferior a la temperatura de ebullición, como ocurre con el agua a $20.0 °C$. El líquido en un recipiente cerrado a una temperatura fija se evapora hasta que la presión del gas alcanza un cierto valor, llamado presión de vapor, que depende del gas y la temperatura.
En este equilibrio, si se agrega calor, parte del líquido se evaporará, y si se elimina el calor, parte del gas se condensará; las moléculas se unen al líquido o forman gotas suspendidas. Si no hay suficiente líquido para que el gas alcance la presión de vapor en el contenedor, todo el líquido finalmente se evapora. Si la presión de vapor del líquido es mayor que la presión ambiente total, incluida la de cualquier aire (u otro gas), el líquido se evapora rápidamente; en otras palabras, hierve. Por lo tanto, el punto de ebullición de un líquido a una presión dada es la temperatura a la que su presión de vapor es igual a la presión ambiental. Las fases líquida y gaseosa están en equilibrio a la temperatura de ebullición ().
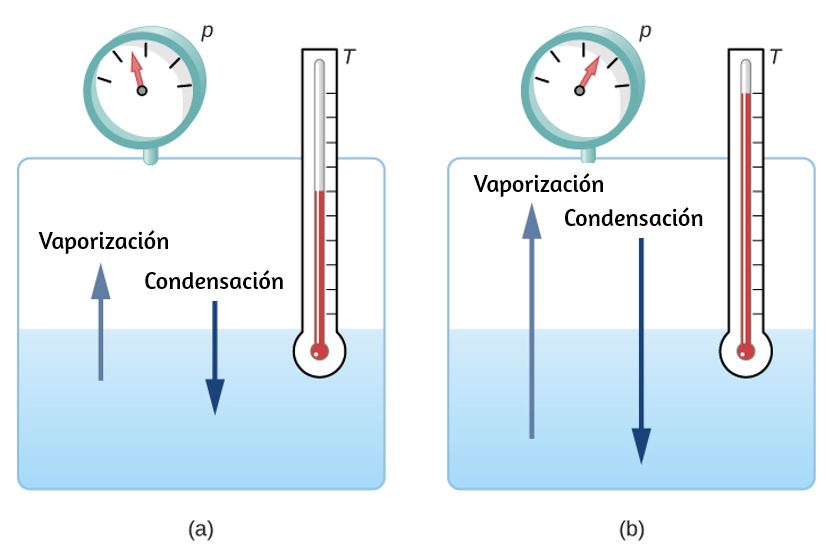
Si una sustancia se encuentra en un recipiente cerrado en el punto de ebullición, entonces el líquido está hirviendo y el gas se está condensando a la misma velocidad sin un cambio neto en sus cantidades.
Para el agua, $100 °C$ es el punto de ebullición a $1.00 atm$, por lo que el agua y el vapor deberían existir en equilibrio en estas condiciones. ¿Por qué una olla de agua abierta a $100 °C$ hierve completamente? El gas que rodea una olla abierta no es agua pura: se mezcla con aire. Si el agua pura y el vapor están en un recipiente cerrado a $100 °C$ y $1,00 atm$, coexistirán, pero con aire sobre la olla, hay menos moléculas de agua para condensar y el agua se evapora. Otra forma de ver esto es que en el punto de ebullición, la presión de vapor es igual a la presión ambiental. Sin embargo, parte de la presión ambiental se debe al aire, por lo que la presión del vapor es menor que la presión de vapor a esa temperatura y la evaporación continúa. A propósito, la presión de vapor de equilibrio de los sólidos no es cero, un hecho que explica la sublimación.
 Comprueba tu aprendizaje 1.4
Comprueba tu aprendizaje 1.4
Hasta ahora, hemos discutido las transferencias de calor que causan el cambio de temperatura. Sin embargo, en una transición de fase, la transferencia de calor no causa ningún cambio de temperatura. Para un ejemplo de cambios de fase, considera la adición de calor a una muestra de hielo a $-20 °C$ () y presión atmosférica. La temperatura del hielo aumenta linealmente, absorbiendo calor a una velocidad constante de $2090 J/kg \cdot °C$ hasta que alcanza los $0 °C$.
Una vez a esta temperatura, el hielo comienza a derretirse y continúa hasta que se haya derretido completamente, absorbiendo $333 kJ/kg$ de calor. La temperatura permanece constante a $0 °C$ durante este cambio de fase. Una vez que todo el hielo se ha derretido, la temperatura del agua líquida aumenta, absorbiendo calor a una nueva tasa constante de $4186 J/kg \cdot °C$. A $100 °C$, el agua comienza a hervir.
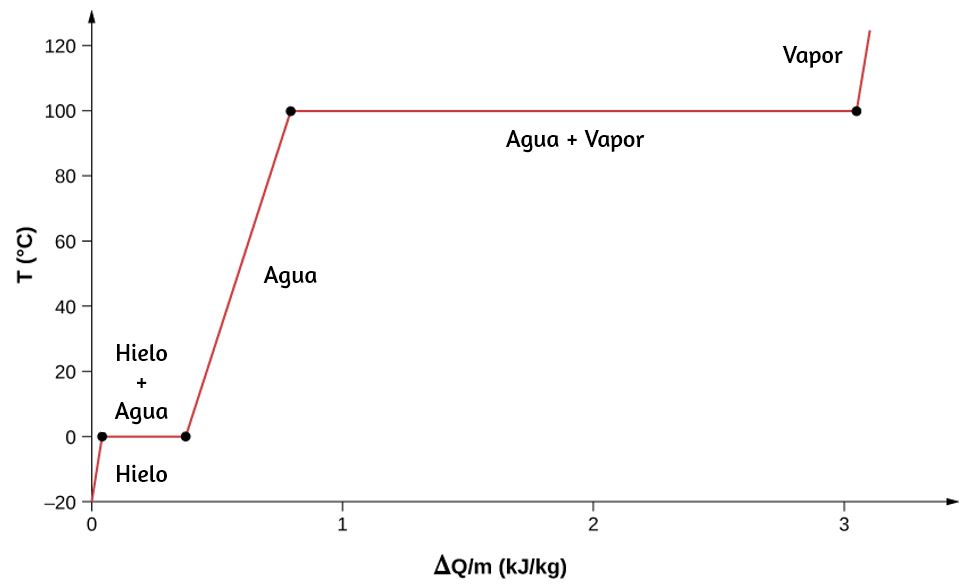
Cuando todo el líquido se ha convertido en vapor, la temperatura aumenta nuevamente, absorbiendo calor a una tasa de $2020 J/kg \cdot °C$. Si comenzamos con vapor y lo enfriamos para hacerlo condensar en agua líquida y congelarlo en hielo, el proceso se invertiría exactamente, con la temperatura nuevamente constante durante cada transición de fase.
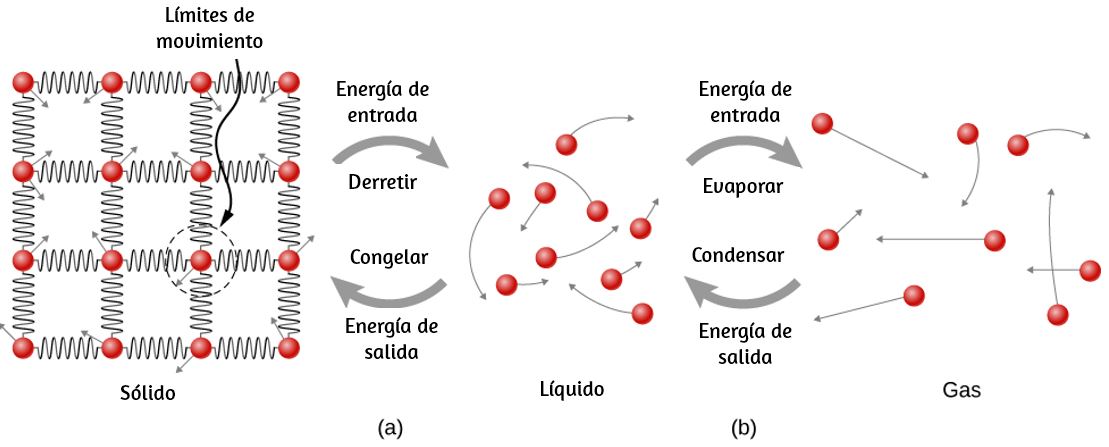
¿Dónde se agrega el calor durante la fusión o la ebullición, teniendo en cuenta que la temperatura no cambia hasta que se complete la transición? Se necesita energía para fundir un sólido, porque las fuerzas de atracción entre las moléculas en el sólido deben romperse, de modo que en el líquido, las moléculas puedan moverse a energías cinéticas comparables; por lo tanto, no hay aumento en la temperatura. Se necesita energía para vaporizar un líquido por razones similares. Por el contrario, el trabajo se realiza mediante fuerzas atractivas cuando las moléculas se juntan durante la congelación y la condensación. Esa energía debe transferirse fuera del sistema, generalmente en forma de calor, para permitir que las moléculas permanezcan juntas (). Por lo tanto, la condensación ocurre en asociación con objetos fríos: el vidrio en la , por ejemplo.
La energía liberada cuando se congela un líquido es utilizada por los productores de naranjas cuando la temperatura se aproxima a $0 ° C$. Los productores rocían agua sobre los árboles para que el agua se congele y el calor se libere a las naranjas en crecimiento. Esto evita que la temperatura dentro de la naranja caiga por debajo del punto de congelación, lo que dañaría la fruta ().
La energía involucrada en un cambio de fase depende de la cantidad de enlaces o pares de fuerzas y su resistencia.


El número de enlaces es proporcional al número de moléculas y, por lo tanto, a la masa de la muestra. La energía por unidad de masa requerida para cambiar una sustancia de la fase sólida a la fase líquida, o liberada cuando la sustancia cambia de líquido a sólido, se conoce como el calor de fusión. La energía por unidad de masa requerida para cambiar una sustancia de la fase líquida a la fase de vapor se conoce como el calor de vaporización. La resistencia de las fuerzas depende del tipo de moléculas. El calor $Q$ absorbido o liberado en un cambio de fase en una muestra de masa $m$ viene dado por
donde el calor latente de fusión $L_f$ y el calor latente de vaporización $L_v$ son constantes materiales que se determinan experimentalmente (Los calores latentes también se llaman coeficientes de calor latente y calores de transformación). Estas constantes están "latentes" u ocultas, porque en los cambios de fase, la energía entra o sale de un sistema sin causar un cambio de temperatura en el sistema, por lo que, en efecto, la energía está oculta.
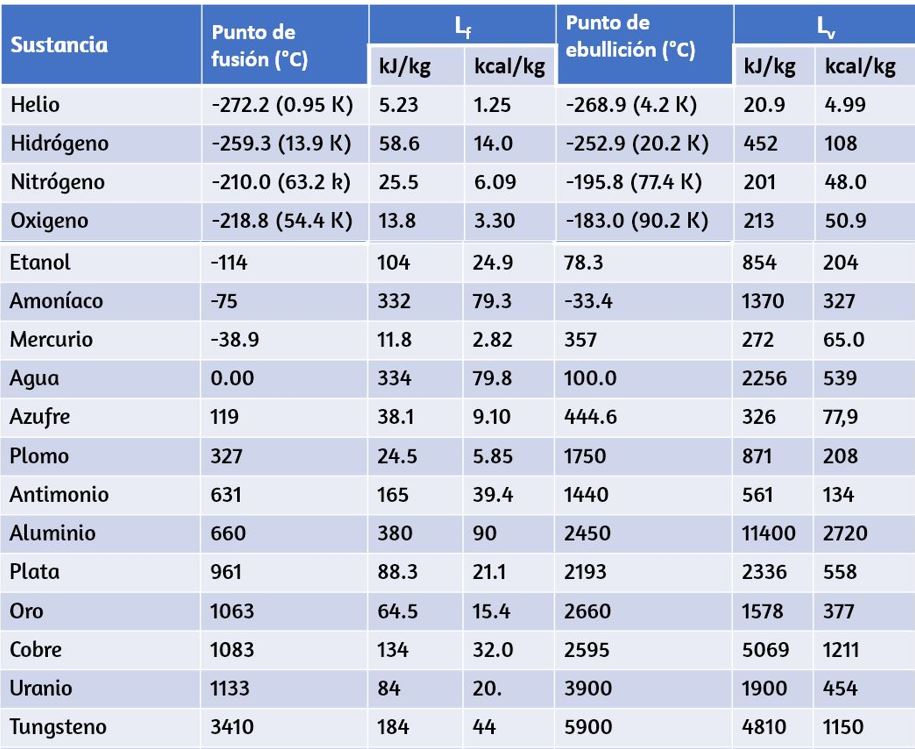
La enumera los valores representativos de $L_f$ y $L_v$ en $kJ/kg$, junto con los puntos de fusión y ebullición. Ten en cuenta que, en general, $L_v > L_f$. La tabla muestra que las cantidades de energía involucradas en los cambios de fase pueden ser fácilmente comparables o mayores que las involucradas en los cambios de temperatura, como también se mostró en la .
El helio no tiene fase sólida a la presión atmosférica. El punto de fusión dado es a una presión de $2.5 MPa$. A $37.0 °C$ (temperatura corporal), el calor de vaporización $L_v$ para el agua es de $2430 kJ/kg$ o $580 kcal/kg$.
Los cambios de fase pueden tener un fuerte efecto estabilizador en las temperaturas que no están cerca de los puntos de fusión y ebullición, ya que la evaporación y la condensación se producen incluso a temperaturas inferiores al punto de ebullición.
Por ejemplo, la temperatura del aire en climas húmedos raramente supera los $38.0 °C$ porque la mayor transferencia de calor se produce al evaporar el agua al aire. De forma similar, las temperaturas en tiempo húmedo rara vez caen por debajo del punto de rocío, la temperatura en que se produce la condensación dada la concentración de vapor de agua en el aire, porque se libera tanto calor cuando se condensa el vapor de agua.
Se necesita más energía para evaporar el agua por debajo del punto de ebullición que en el punto de ebullición, porque la energía cinética de las moléculas de agua a temperaturas inferiores a $100 °C$ es menor que a $100 °C$, por lo que se dispone de menos energía de movimientos térmicos aleatorios. Por ejemplo, a la temperatura corporal, la evaporación del sudor de la piel requiere una entrada de calor de $2428 kJ/kg$, que es aproximadamente un $10$% más alta que el calor latente de vaporización a $100 °C$. Este calor proviene de la piel, y este efecto de enfriamiento por evaporación de la sudoración ayuda a reducir la temperatura corporal en climas cálidos. Sin embargo, la alta humedad inhibe la evaporación, por lo que la temperatura corporal puede aumentar, mientras que el sudor no evaporado puede quedar en la frente.
Ejemplo 1.9
Cálculo de la temperatura final a partir del cambio de fase
Se usan tres cubitos de hielo para enfriar una gaseosa a $20 °C$ con masa $m_{\textsf{soda}} = 0.25 kg$. El hielo está a $0 °C$ y cada cubito de hielo tiene una masa de $6.0 g$. Supón que la gaseosa se guarda en un recipiente de espuma para que la pérdida de calor pueda despreciarse y que la gaseosa tenga el mismo calor específico que el agua. Encuentra la temperatura final cuando todo el hielo se haya derretido.
Estrategia
Los cubitos de hielo están a la temperatura de fusión de $0 °C$. El calor se transfiere de la soda al hielo para derretirse. La fusión produce agua a $0 °C$, por lo que se transfiere más calor desde la soda a esta agua hasta que el sistema de agua más soda alcanza el equilibrio térmico.
El calor transferido al hielo es
$$Q_{\textsf{hielo}} = m_{\textsf{hielo}}L_f + m_{\textsf{hielo}}c_w(T_f - 0 °C)$$El calor emitido por la soda es
$$Q_{\textsf{soda}} = m_{\textsf{soda}}c_w(T_f - 20 °C)$$Como no se pierde calor, $Q_{\textsf{hielo}} = -Q_{\textsf{soda}}$, como en el Ejemplo 1.7, de modo que
$$m_{\textsf{hielo}}L_f + m_{\textsf{hielo}}c_w(T_f - 0 °C) = -m_{\textsf{soda}}c_w(T_f - 20 °C)$$Resolviendo por la cantidad desconocida T_f:
$$T_f = \frac{m_{\textsf{soda}}cW(20 °C) - m_{\textsf{hielo}}L_f}{(m_{\textsf{soda}} + m_{\textsf{hielo}})c_w}$$Solución
Primero identificamos las cantidades conocidas. La masa de hielo es $m_{\textsf{hielo}} = 3 × 6,0 g = 0,018 kg$ y la masa de soda es $m_{\textsf{soda}} = 0,25 kg$. Luego calculamos la temperatura final:
$$T_f = \frac{20,930 J − 6012 J}{1122 J/°C} = 13 °C$$Explicación
Este ejemplo ilustra las grandes energías involucradas durante un cambio de fase. La masa de hielo es aproximadamente el $7$% de la masa de la soda, pero conduce a un cambio notable en la temperatura de la soda. Aunque supusimos que el hielo estaba a la temperatura de congelación, esto no es realista para el hielo recién salido del congelador: la temperatura típica es de $-6 °C$.
Sin embargo, esta corrección no cambia significativamente el resultado que encontramos. ¿Puedes explicar porque?
Al igual que las transiciones sólido-líquido y líquido-vapor, las transiciones directas de vapor sólido o sublimaciones implican calor. La energía transferida viene dada por la ecuación $Q = mL_s$, donde $L_s$ es el calor de sublimación, análogo a $L_f$ y $L_v$. El calor de la sublimación a una temperatura dada es igual al calor de fusión más el calor de vaporización a esa temperatura.
Ahora podemos calcular cualquier cantidad de efectos relacionados con la temperatura y el cambio de fase. En cada caso, es necesario identificar qué cambios de temperatura y fase están teniendo lugar. Ten en cuenta que la transferencia de calor y el trabajo pueden causar cambios de temperatura y fase.
Estrategia de resolución de problemas: los efectos de la transferencia de calor
1. Examina la situación para determinar si hay un cambio en la temperatura o fase. ¿Hay transferencia de calor dentro o fuera del sistema? Cuando no es evidente si se produce o no un cambio de fase, es posible que desees resolver el problema primero como si no hubiera cambios de fase, y examinar el cambio de temperatura obtenido. Si es suficiente llevarlo más allá de un punto de ebullición o fusión, debes volver atrás y resolver el problema en pasos: cambio de temperatura, cambio de fase, cambio de temperatura posterior, etc.
2. Identifica y lista todos los objetos que cambian la temperatura o fase.
3. Identifica exactamente qué debe determinarse en el problema (identifica las incógnitas). Una lista escrita es útil.
4.Haz una lista de lo que se da o lo que se puede inferir del problema tal como se establece (identifica los datos conocidos). Si hay un cambio de temperatura, el calor transferido depende del calor específico de la sustancia (transferencia de calor, calor específico y calorimetría), y si hay un cambio de fase, el calor transferido depende del calor latente de la sustancia ().
5. Resuelve la ecuación apropiada para la cantidad que se determinará (la incognita).
6. Sustituye los datos conocidos junto con sus unidades en la ecuación apropiada y obtén soluciones numéricas completas con unidades. Es posible que debas hacer esto en pasos si hay más de un estado en el proceso, como un cambio de temperatura seguido de un cambio de fase. Sin embargo, en un problema de calorimetría, cada paso corresponde a un término en la ecuación única $Q_{\textsf{caliente}} + Q_{\textsf{frío}} = 0$.
7. Verifica la respuesta para ver si es razonable. ¿Tiene sentido? Como ejemplo, asegúrate de que cualquier cambio de temperatura no provoque un cambio de fase que no hayas tenido en cuenta.
 Comprueba tu aprendizaje 1.5
Comprueba tu aprendizaje 1.5
Tan interesante como los efectos de la transferencia de calor en un sistema son los métodos por los cuales ocurre. Cada vez que hay una diferencia de temperatura, se produce transferencia de calor. Puede ocurrir rápidamente, como a través de una bandeja de cocina, o lentamente, como a través de las paredes de un cofre de picnic helado. Tantos procesos implican transferencia de calor que es difícil imaginar una situación donde no se produzca. Sin embargo, cada transferencia de calor se lleva a cabo por solo tres métodos:
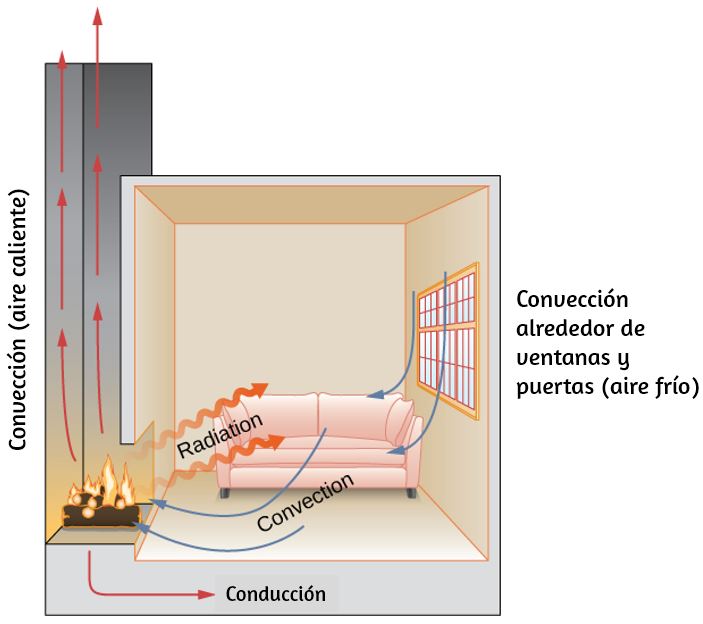
En la ilustración al comienzo de este capítulo, el fuego calienta las caras de los excursionistas de nieve en gran medida por la radiación. La convección les transporta algo de calor, pero la mayor parte del flujo de aire del fuego es hacia arriba (creando la forma familiar de llamas), llevando calor a los alimentos que se cocinan y al cielo.
Los snowshoers usan ropa diseñada con baja conductividad para evitar que el calor salga de sus cuerpos.
En esta sección, examinamos estos métodos con cierto detalle. Cada método tiene características únicas e interesantes, pero los tres tienen dos cosas en común: transfieren calor únicamente debido a una diferencia de temperatura, y cuanto mayor es la diferencia de temperatura, más rápida es la transferencia de calor ().
 Comprueba tu aprendizaje 1.6
Comprueba tu aprendizaje 1.6
Mientras caminas descalzo por la alfombra de la sala de estar en una casa fría y luego pisas el piso de la cocina, tus pies se sienten más fríos sobre la losa. Este resultado es intrigante, ya que la alfombra y el piso de baldosas están a la misma temperatura.
La diferente sensación se explica por las diferentes velocidades de transferencia de calor: la pérdida de calor es más rápida para la piel en contacto con las baldosas que con la alfombra, por lo que la sensación de frío es más intensa.
Algunos materiales conducen la energía térmica más rápido que otros. La muestra un material que conduce el calor lentamente, es un buen aislante térmico o un conductor de calor deficiente, utilizado para reducir el flujo de calor hacia y desde una casa.

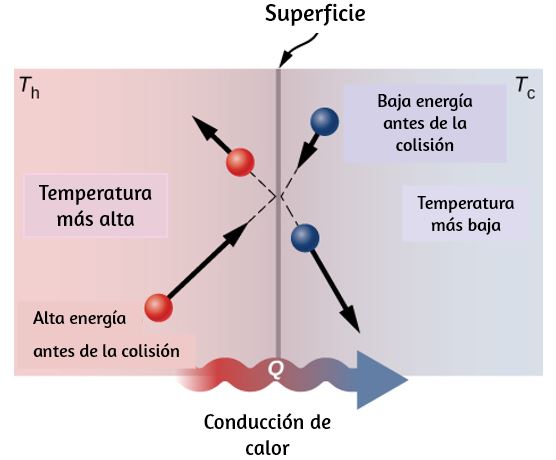
Una imagen molecular de la conducción de calor ayudará a justificar la ecuación que la describe. La muestra moléculas en dos cuerpos a diferentes temperaturas, $T_h$ y $T_c$, para "caliente" (hot) y "frío" (cold). La energía cinética promedio de una molécula en el cuerpo caliente es más alta que en el cuerpo más frío.
La energía cinética promedio de una molécula en el cuerpo caliente es más alta que en el cuerpo más frío. Si dos moléculas colisionan, la energía se transfiere de la molécula de alta energía a la de baja energía. En un metal, la imagen también incluiría electrones de valencia libres colisionando entre sí y con átomos, transfiriendo energía de la misma manera.
El efecto acumulativo de todas las colisiones es un flujo neto de calor desde el cuerpo más caliente al más frío. Por lo tanto, la velocidad de transferencia de calor aumenta al aumentar la diferencia de temperatura $ΔT = T_h - T_c$. Si las temperaturas son las mismas, la tasa de transferencia de calor neta es cero. Debido a que el número de colisiones aumenta al aumentar el área, la conducción de calor es proporcional al área de la sección transversal, un segundo factor en la ecuación.
Una tercera cantidad que afecta la tasa de conducción es el grosor del material a través del cual se transfiere el calor. La muestra una losa de material con una temperatura más alta a la izquierda que a la derecha. Transferencias de calor de izquierda a derecha por una serie de colisiones moleculares. Cuanto mayor sea la distancia entre el calor y el frío, más tiempo tardará el material en transferir la misma cantidad de calor.
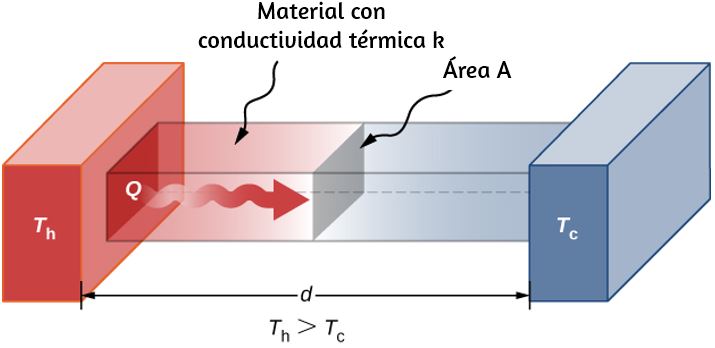
Estas cuatro cantidades aparecen en una ecuación simple deducida y confirmada por experimentos. La tasa de transferencia de calor conductivo a través de una losa de material, como la de la , viene dada por
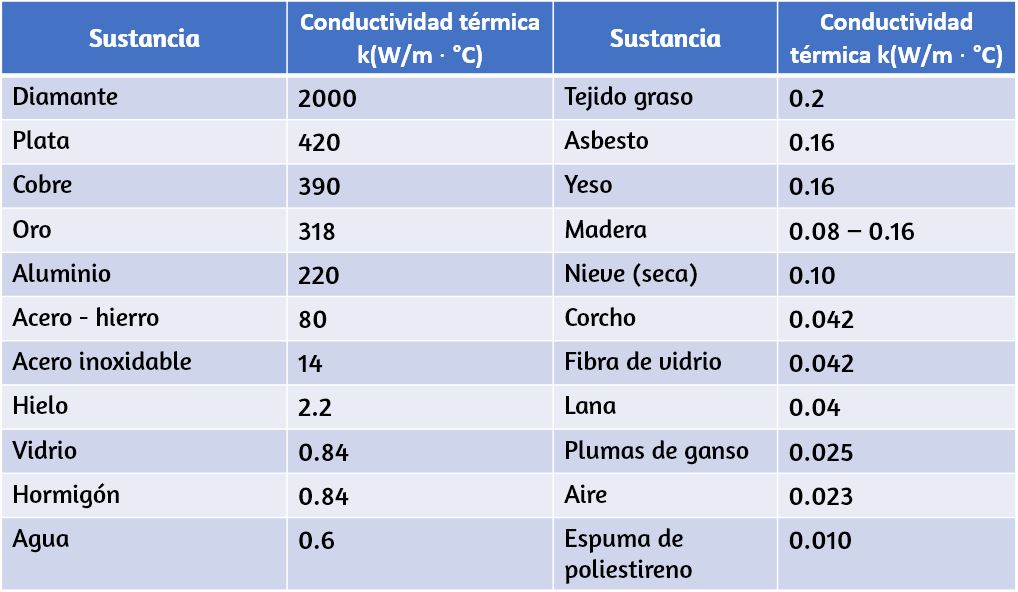
donde $P$ es la potencia o tasa de transferencia de calor en vatios o en kilocalorías por segundo, $A$ y $d$ son el área de la superficie y el espesor, como se muestra en la Figura 1.22, $T_h - T_c$ es la diferencia de temperatura a través de la losa, y $k$ es la conductividad térmica del material. La da los valores representativos de conductividad térmica.
Más generalmente, podemos escribir $P = -kA\frac{dT}{dx}$
donde $x$ es la coordenada en la dirección del flujo de calor. Como en la , la potencia y el área son constantes, $dT/dx$ es constante y la temperatura disminuye linealmente de $TT_h$ a $TT_c$.
Ejemplo 1.10
Cálculo de la transferencia de calor a través de la conducción
Una nevera de poliestireno tiene un área total de $0.950 m^2$ y paredes con un espesor promedio de $2.50 cm$. La nevera contiene hielo, agua y bebidas enlatadas a $0 °C$. El interior de la nevera se mantiene frío al derretir el hielo. ¿Cuánto hielo se derrite en un día si la nevera se guarda en el maletero de un automóvil a $35.0 °C$?
Estrategia
Esta pregunta involucra tanto calor para un cambio de fase (fusión del hielo) como la transferencia de calor por conducción. Para encontrar la cantidad de hielo derretido, debemos encontrar el calor neto transferido. Este valor se puede obtener calculando la tasa de transferencia de calor por conducción y multiplicando por el tiempo.
Solución
Primero identificamos los datos conocidos.
$k = 0.010 W/m \cdot °C$ para espuma de poliestireno; $A = 0.950 m^2$; $d = 2,50 cm = 0,0250 m$; $T_c = 0 °C$; $T_h = 35,0 °C$; $t = 1$ día $= 24$ horas $= 84,400 s$.
Luego identificamos las incógnitas. Necesitamos hallar la masa del hielo, $m$. También necesitamos hallar el calor neto transferido para derretir el hielo, $Q$. La tasa de transferencia de calor por conducción está dada por
$$P = \frac{dQ}{dT} = \frac{kA(T_h - T_c)}{d}$$El calor utilizado para derretir el hielo es $Q = mL_f$. Sustituimos los valores conocidos:
$$P = \frac{(0.010 W/m \cdot °C)(0.950 m^2)(35.0 °C − 0 °C)}{0.0250 m} = 13.3 W$$Al multiplicar la tasa de transferencia de calor por el tiempo ($1$ día $= 86,400 s$), obtenemos: $Q = Pt = (13.3 W)(86.400 s) = 1.15 × 10^6 J$
Configuramos esto igual al calor transferido para derretir el hielo, $Q = mL_f$, y hallamos la masa $m$:
$$m = \frac{Q}{L_f} = \frac{1.15 × 10^6 J}{334 × 10^3 J/kg} = 3.44 kg$$Explicación
El resultado de $3,44 kg$, o alrededor de $7,6 lb$, parece correcto, según la experiencia. Puedes esperar usar una bolsa de hielo de $4 kg$ ($7 - 10 lb$) por día. Se necesita un poco de hielo adicional si agregas alimentos o bebidas calientes.
La muestra que la espuma de poliestireno es un conductor muy pobre y, por lo tanto, un buen aislante. Otros buenos aislantes incluyen fibra de vidrio, lana y plumas de ganso. Al igual que la espuma de poliestireno, todos estos contienen muchas pequeñas bolsas de aire, aprovechando la mala conductividad térmica del aire.
Al desarrollar el aislamiento, cuanto menor es la conductividad $k$ y cuanto mayor sea el grosor $d$, mejor. Por lo tanto, la relación $d/k$, llamada factor $R$, es grande para un buen aislante. La tasa de transferencia de calor conductivo es inversamente proporcional a $R$. Los factores $R$ se citan más comúnmente para aislamiento doméstico, refrigeradores y similares.
Desafortunadamente, en los Estados Unidos, R sigue estando en unidades no métricas de $ft^2 \cdot °F \cdot h/Btu$, aunque la unidad generalmente no se expresa [$1$ unidad térmica británica ($Btu$) es la cantidad de energía necesaria para cambiar la temperatura de $1.0 lb$ de agua por $1.0 °F$, que es $1055.1 J$]. Un par de valores representativos son un factor $R$ de $11$ para las piezas de fibra de vidrio de aislamiento de $3,5$ pulgadas de grosor, y un factor $R$ de $19$ para las piezas de fibra de vidrio de $6.5$ pulgadas de grosor (). En los Estados Unidos, las paredes suelen estar aisladas con bloques de $3,5$ pulgadas, mientras que los techos suelen estar aislados con bloques de $6,5$ pulgadas. En climas fríos, se pueden usar bloques más gruesos.

Ten en cuenta que en la , la mayoría de los mejores conductores térmicos (plata, cobre, oro y aluminio) también son los mejores conductores eléctricos, ya que contienen muchos electrones libres que pueden transportar energía térmica (El diamante, un aislante eléctrico, conduce el calor por vibraciones atómicas). Los utensilios de cocina generalmente están hechos de buenos conductores, pero los mangos están hechos de buenos aislantes (malos conductores).
Ejemplo 1.11
Dos conductores de extremo a extremo
Una varilla de acero y una varilla de aluminio, cada una con un diámetro de $1.00 cm$ y una longitud de $25.0 cm$, están soldadas de extremo a extremo. Un extremo de la varilla de acero se coloca en un tanque grande de agua hirviendo a $100 °C$, mientras que el otro extremo de la varilla de aluminio se coloca en un tanque grande de agua a $20 °C$. Las varillas están aisladas para que no se escape el calor de sus superficies ¿Cuál es la temperatura en la articulación y cuál es la tasa de conducción de calor a través de esta varilla compuesta?
Estrategia
El calor que entra en la varilla de acero desde el agua hirviendo no tiene lugar a donde ir sino a través de la varilla de acero, luego a través de la varilla de aluminio, hasta el agua fría. Por lo tanto, podemos equiparar la tasa de conducción a través del acero con la tasa de conducción a través del aluminio.
Repetimos el cálculo con un segundo método, en el cual usamos la resistencia térmica $R$ de la varilla, ya que simplemente se agrega cuando dos varillas se unen de punta a punta.
Solución
La longitud de cada varilla es $L_{\textsf{Al}} = L_{\textsf{acero}} = 0.25 m$, el área de sección transversal de cada varilla es $A_{\textsf{Al}} = A_{\textsf{acero}} = 7.85 × 10^{-5} m^2$, la conductividad térmica del aluminio es $k_{\textsf{Al}} = 220 W/m \cdot °C$, la conductividad térmica de acero es $k_{\textsf{acero}} = 80 W/m \cdot °C$, la temperatura en el extremo caliente es $T = 100 °C$, y la temperatura en el extremo frío es $T = 20 °C$.
Segundo método de Solución
Por lo tanto, simplemente podemos agregar factores $R$. Ahora, $P = \dfrac{80 °C}{A(R_{\textsf{acero}} + R_{\textsf{Al}})}$
y
$$R_{\textsf{Al}} = 1.14 × 10^{−3} m^2 \cdot °C/W$$entonces, $T = 20 °C + 21.3 °C = 41.3 °C$, como en la Solución anterior.
Explicación
En la práctica, es común agregar valores $R$, como en el cálculo del valor $R$ de una pared aislada. En la situación análoga en electrónica, la resistencia corresponde a $AR$ en este problema y es aditiva incluso cuando las áreas son desiguales, como es común en la electrónica. Nuestra ecuación para la conducción de calor puede usarse solo cuando las áreas son iguales; de lo contrario, tendríamos un problema en el flujo de calor tridimensional, que está más allá de nuestro alcance.
 Comprueba tu aprendizaje 1.7
Comprueba tu aprendizaje 1.7
La conducción es causada por el movimiento aleatorio de átomos y moléculas. Como tal, es un mecanismo ineficaz para el transporte de calor sobre distancias macroscópicas y tiempos cortos.
Por ejemplo, la temperatura en la Tierra sería insoportablemente fría durante la noche y extremadamente cálida durante el día si el transporte de calor en la atmósfera fuera solo por conducción. Además, los motores de los automóviles se sobrecalentarían a menos que hubiera una forma más eficiente de eliminar el exceso de calor de los pistones. El siguiente módulo discute el importante mecanismo de transferencia de calor en tales situaciones.
El siguiente vídeo y los interactivos de las páginas siguientes, hacen parte del proyecto @prende.mx, dirigido por el Dr. José Luis Abreu León
En la siguiente escena interactiva, selecciona el material entre aluminio, madera, plata y acero y luego inicia la simulación para cómo se realiza la conducción a lo largo de la cuchara. Para observar mejor la escena, puedes hacer clic en el botón "Ampliar"
 Comprueba tu aprendizaje - Test de Falso y Verdadero
Comprueba tu aprendizaje - Test de Falso y Verdadero
En la convección, la energía térmica es transportada por el flujo de materia a gran escala. Se puede dividir en dos tipos. En la convección forzada, el flujo es impulsado por ventiladores, bombas y similares. Un ejemplo simple es un ventilador que sopla aire en los alrededores calientes y lo refresca reemplazando el aire calentado por su cuerpo con aire más frío. Un ejemplo más complicado es el sistema de enfriamiento de un automóvil típico, en el que una bomba mueve refrigerante a través del radiador y el motor para enfriar el motor y un ventilador sopla aire para enfriar el radiador.
En la convección libre o natural, el flujo es impulsado por fuerzas de flotación: el fluido caliente se eleva y el fluido frío se hunde porque la densidad disminuye a medida que aumenta la temperatura. La casa de la se mantiene caliente por convección natural, al igual que la olla de agua en la estufa de la . Las corrientes oceánicas y la circulación atmosférica a gran escala, que resultan de la flotabilidad del aire caliente y el agua, transfieren el aire caliente de los trópicos hacia los polos y el aire frío desde los polos hacia los trópicos (La rotación de la Tierra interactúa con esos flujos, causando el flujo de aire observado hacia el este en las zonas templadas).
La convección suele ser más complicada que la conducción. Además de notar que la tasa de convección es a menudo aproximadamente proporcional a la diferencia de temperatura, no haremos ningún trabajo cuantitativo comparable a la fórmula para la conducción. Sin embargo, podemos describir la convección cualitativamente y relacionar las tasas de convección con el calor y el tiempo. Sin embargo, el aire es un mal conductor. Por lo tanto, la convección domina la transferencia de calor por aire, y la cantidad de espacio disponible para el flujo de aire determina si el aire transfiere calor rápidamente o lentamente. Hay poca transferencia de calor en un espacio lleno de aire con una pequeña cantidad de otro material que impide el flujo.
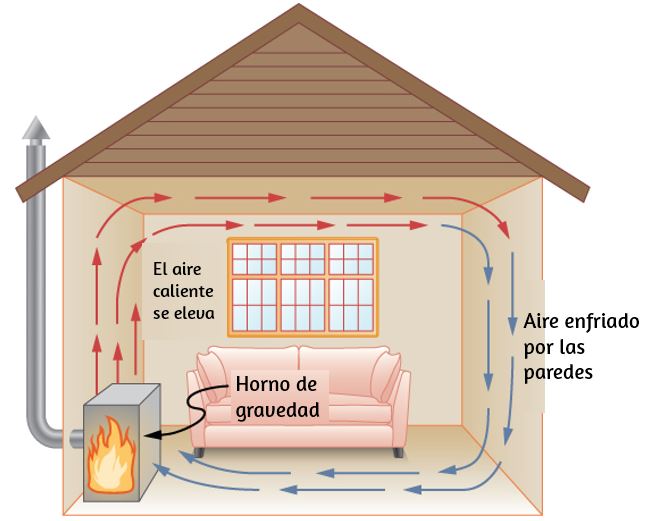
El espacio entre las paredes interiores y exteriores de una casa típica estadounidense, por ejemplo, es de aproximadamente $9 cm$ ($3,5$ pulgadas), lo suficientemente grande como para que la convección funcione con eficacia. La adición de aislamiento de pared evita el flujo de aire, por lo que disminuye la pérdida de calor (o ganancia). Por otro lado, el espacio entre los dos paneles de una ventana de doble pared es de aproximadamente $1 cm$, lo que evita en gran medida la convección y aprovecha la baja conductividad del aire para reducir la pérdida de calor.
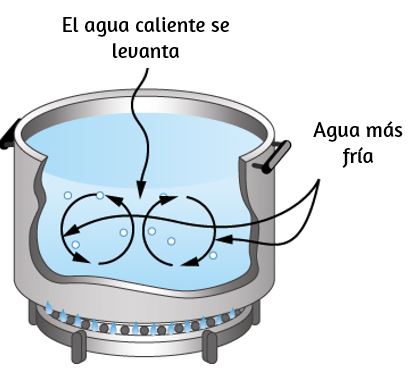
La piel, la tela y la fibra de vidrio también aprovechan la baja conductividad del aire al atraparlo en espacios demasiado pequeños para soportar la convección ().
Algunos fenómenos interesantes ocurren cuando la convección va acompañada de un cambio de fase. La combinación nos permite refrescarnos sudando incluso si la temperatura del aire circundante excede la temperatura corporal. Se requiere calor de la piel para que el sudor se evapore de la piel, pero sin flujo de aire, el aire se satura y la evaporación se detiene. El flujo de aire causado por la convección reemplaza el aire saturado por aire seco y la evaporación continúa.
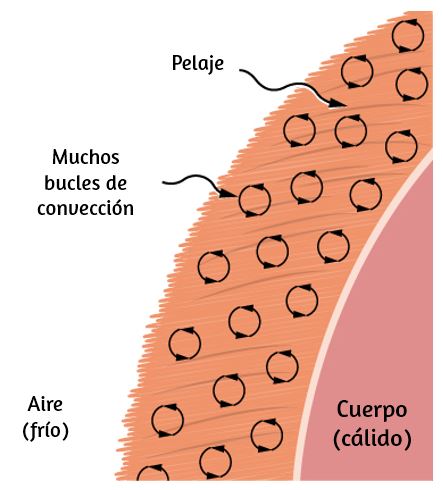
Ejemplo 1.12
Cálculo del flujo de masa durante la convección
Una persona promedio produce calor a una velocidad de aproximadamente $120 W$ cuando está en reposo. ¿A qué velocidad debe evaporarse el agua del cuerpo para deshacerse de toda esta energía?
Por simplicidad, suponemos que esta evaporación ocurre cuando una persona está sentada a la sombra y las temperaturas circundantes son las mismas que la temperatura de la piel, eliminando la transferencia de calor por otros métodos.
Estrategia
Se necesita energía para este cambio de fase ($Q = mL_v$). Por lo tanto, la pérdida de energía por unidad de tiempo es
$$\frac{Q}{t} = \frac{mL_v}{t} = 120 W = 120 J/s$$Dividimos ambos lados de la ecuación por $L_v$ para encontrar que la masa evaporada por unidad de tiempo
$$\frac{m}{t} = \frac{120 J/s}{L_v}$$Solución
Inserta el valor del calor latente de la , $L_v = 2430 kJ/kg = 2430 J/g$. Esto produce
$$\frac{m}{t} = \frac{120 J/s}{2430 J/g} = 0.0494 g/s = 2.96g/min$$Explicación
Evaporar aproximadamente $3 g/min$ parece razonable. Esto sería aproximadamente $180 g$ ($7$ onzas) por hora. Si el aire está muy seco, el sudor puede evaporarse sin que se note. Una cantidad significativa de evaporación también tiene lugar en los pulmones y vías de respiración.
Otro ejemplo importante de la combinación de cambio de fase y convección ocurre cuando el agua se evapora de los océanos. El calor se elimina del océano cuando el agua se evapora. Si el vapor de agua se condensa en gotas líquidas a medida que se forman las nubes, posiblemente lejos del océano, se libera calor en la atmósfera.
Por lo tanto, hay una transferencia general de calor del océano a la atmósfera. Este proceso es el poder conductor detrás de los nubarrones, esos grandes cúmulos que se elevan hasta $20.0 km$ hacia la estratosfera (). El vapor de agua transportado por convección se condensa y libera enormes cantidades de energía. Esta energía hace que el aire se expanda y suba a altitudes más frías. Se produce más condensación en estas regiones, lo que a su vez impulsa la nube aún más. Este mecanismo es un ejemplo de retroalimentación positiva, ya que el proceso se refuerza y se acelera a sí mismo. A veces produce tormentas violentas, con relámpagos y granizo. El mismo mecanismo impulsa los huracanes.
 Comprueba tu aprendizaje 1.8
Comprueba tu aprendizaje 1.8

Las escenas interactivas de las páginas siguientes, hacen parte del proyecto @prende.mx, dirigido por el Dr. José Luis Abreu León
La primera escena, presenta algunos ejemplos de transmisión de calor por convección.
La segunda escena, permite explorar la transmisión de calor por convección, especialmente en corrientes de agua, tanto en la tierra como en el aire.
La tercera escena es un test de falso y verdadero, para probar tu aprendizaje hasta este punto.
En este escena interactiva se presentan tres ejemplos de cómo se transmite el calor por convección. Los tres ejemplos se muestran de igual número de vídeos, los cuales puedes detener o reiniciar en cualquier momento.
Haz clic en el botón "Siguiente" para observar y analizar los ejemplos.
En esta escena interactiva, presta atención a la simulación que muestra cómo las moléculas de agua se mueven hacia arriba y hacia abajo del recipiente según su temperatura. Explora cómo funciona la corriente por convección.
Haz clic en el botón "Siguiente" para observar la simulación.
 Comprueba tu aprendizaje - Test de Falso y Verdadero
Comprueba tu aprendizaje - Test de Falso y Verdadero
Puedes sentir la transferencia de calor del sol. El espacio entre la Tierra y el Sol está en gran parte vacío, por lo que el Sol nos calienta sin posibilidad de transferencia de calor por convección o conducción. De manera similar, a veces se puede decir que el horno está caliente sin tocar su puerta ni mirar adentro; puede que te caliente cuando pasas caminando. En estos ejemplos, el calor se transfiere por radiación (). Es decir, el cuerpo caliente emite ondas electromagnéticas que son absorbidas por la piel. No se requiere medio para que las ondas electromagnéticas se propaguen. Los nombres diferentes se usan para ondas electromagnéticas de diferentes longitudes de onda: ondas de radio, microondas, radiación infrarroja, luz visible, radiación ultravioleta, rayos X y rayos gamma.

La energía de la radiación electromagnética varía en un amplio rango, dependiendo de la longitud de onda: una longitud de onda más corta (o una frecuencia más alta) corresponde a una energía más alta. Debido a que se irradia más calor a temperaturas más altas, las temperaturas más altas producen más intensidad en cada longitud de onda, pero especialmente en longitudes de onda más cortas. En la luz visible, la longitud de onda determina el color: el rojo tiene la longitud de onda más larga y el violeta el más corta, por lo que un cambio de temperatura va acompañado de un cambio de color.
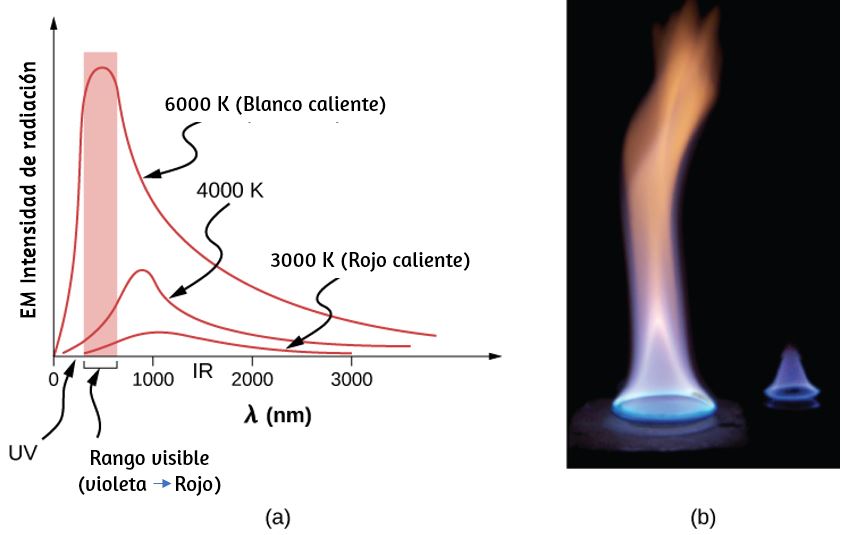
Por ejemplo, un elemento de calefacción eléctrica en una estufa brilla de rojo a naranja, mientras que el acero de mayor temperatura en un alto horno se ilumina de amarillo a blanco. La radiación infrarroja es la forma predominante radiada por objetos más fríos que el elemento eléctrico y el acero. La energía radiada en función de la longitud de onda depende de su intensidad, que se representa en la por la altura de la distribución.
La tasa de transferencia de calor por radiación también depende del color del objeto. El negro es el más efectivo, y el blanco es el menos efectivo. En un día claro de verano, el asfalto negro en un estacionamiento es más caliente que la acera gris adyacente, porque el negro absorbe mejor que el gris ().

Lo contrario también es cierto: el negro irradia mejor que el gris. Por lo tanto, en una clara noche de verano, el asfalto es más frío que la acera gris, porque el negro irradia la energía más rápidamente que el gris. Un objeto perfectamente negro sería un radiador ideal y un absorbente ideal, ya que capturaría toda la radiación que caiga sobre él. En contraste, un objeto perfectamente blanco o un espejo perfecto reflejaría toda la radiación, y un objeto perfectamente transparente lo transmitiría todo (). Tales objetos no emitirían ninguna radiación. Matemáticamente, el color está representado por la emisividad $e$. Un radiador de "cuerpo negro" tendría una $e = 1$, mientras que un reflector o transmisor perfecto tendría $e = 0$.
Para ejemplos reales, los filamentos de la bombilla de tungsteno tienen una e de aproximadamente $0,5$, y el negro de humo (un material utilizado en el tóner de la impresora) tiene una emisividad de aproximadamente $0,95$.
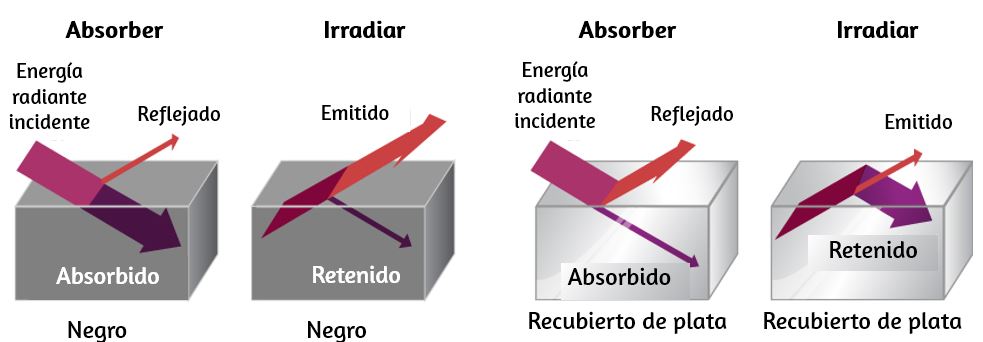
Para ver eso, considera un objeto plateado y un objeto negro que pueden intercambiar calor por radiación y están en equilibrio térmico.
Sabemos por experiencia que se mantendrán en equilibrio (el resultado de un principio que se discutirá detalladamente en la Segunda Ley de la Termodinámica). Para que la temperatura del objeto negro permanezca constante, debe emitir tanta radiación como absorbe, por lo que debe ser tan buena tanto radiante como absorbente. Consideraciones similares muestran que el objeto plateado debe irradiar tan poco como absorbe. Por lo tanto, una propiedad, la emisividad, controla tanto la radiación como la absorción.
Finalmente, el calor irradiado es proporcional al área superficial del objeto, ya que cada parte de la superficie se irradia. Si separas los carbones de un incendio, la radiación aumenta notablemente debido a un aumento en el área de superficie radiante.
La tasa de transferencia de calor emitida por la radiación se describe en la ley de radiación de Stefan-Boltzmann:
$$P = σAeT^4$$donde $σ = 5.67 × 10^{-8}J/s \cdot m^2 \cdot K^4$ es la constante de Stefan-Boltzmann, una combinación de constantes fundamentales de la naturaleza, $A$ es el área de superficie del objeto, y $T$ es su temperatura en kelvins.
La proporcionalidad a la cuarta potencia de la temperatura absoluta es una dependencia de temperatura notablemente fuerte. Permite la detección de incluso pequeñas variaciones de temperatura. Las imágenes llamadas termógrafos se pueden usar médicamente para detectar regiones de temperatura anormalmente altas en el cuerpo, lo que puede indicar una enfermedad.
Se pueden usar técnicas similares para detectar fugas de calor en los hogares (), optimizar el rendimiento de los altos hornos, mejorar los niveles de confort en los entornos de trabajo e incluso asignar de forma remota el perfil de temperatura de la Tierra.
La ecuación de Stefan-Boltzmann solo necesita un ligero refinamiento para tratar un caso simple de absorción de radiación por parte de un objeto de su entorno. Suponiendo que un objeto con una temperatura $T_1$ está rodeado por un entorno con una temperatura uniforme $T_2$, la tasa neta de transferencia de calor por radiación es
donde $e$ es la emisividad del objeto solo. En otras palabras, no importa si el entorno es blanco, gris o negro: el equilibrio de radiación dentro y fuera del objeto depende de qué tan bien emite y absorbe la radiación. Cuando $T_2 > T_1$, la cantidad de $P_{\textsf{neta}}$ es positiva, es decir, la transferencia de calor neta es de caliente a fría.

Antes de dar un ejemplo, tenemos una complicación para discutir: diferentes emisividades en diferentes longitudes de onda. Si la fracción de radiación incidente que refleja un objeto es la misma en todas las longitudes de onda visibles, el objeto es gris; si la fracción depende de la longitud de onda, el objeto tiene algún otro color. Por ejemplo, un objeto rojo o rojizo refleja la luz roja con más fuerza que otras longitudes de onda visibles. Como absorbe menos rojo, irradia menos rojo cuando está caliente. La reflexión diferencial y la absorción de longitudes de onda fuera del rango visible no tienen ningún efecto sobre lo que vemos, pero pueden tener efectos físicos importantes.
La piel es un muy buen absorbente y emisor de radiación infrarroja, que tiene una emisividad de $0.97$ en el espectro infrarrojo. Por lo tanto, a pesar de las variaciones obvias en el color de la piel, todos somos casi negros en el infrarrojo. Esta alta emisividad de infrarrojos es la razón por la cual podemos sentir fácilmente la radiación en nuestra piel. También es la base para la efectividad de los alcances de visión nocturna utilizados por las fuerzas del orden público y el ejército para detectar a los seres humanos.
Ejemplo 1.13
Cálculo de la transferencia de calor neto de una persona
¿Cuál es la tasa de transferencia de calor por radiación de una persona desvestida de pie en una habitación oscura cuya temperatura ambiente es de $22.0 °C$? La persona tiene una temperatura normal de la piel de $33.0 °C$ y una superficie de $1.50 m^2$. La emisividad de la piel es $0.97$ en el infrarrojo, la parte del espectro donde se produce la radiación.
Estrategia
Podemos resolver esto usando la ecuación para la tasa de transferencia de calor radiactivo.
Solución
Sustituye los valores de temperatura $T_2 = 295 K$ y $T_1 = 306 K$, de modo que
Explicación
Este valor es una tasa significativa de transferencia de calor al medio ambiente (ten en cuenta el signo menos), teniendo en cuenta que una persona en reposo puede producir energía a razón de $125 W$ y que la conducción y la convección también transfieren energía al medio ambiente. De hecho, probablemente esperaríamos que esta persona tenga frío.
La ropa reduce significativamente la transferencia de calor al medio ambiente por todos los mecanismos, ya que la ropa ralentiza la conducción y la convección, y tiene una emisividad menor que la piel (especialmente si es de color claro).
La temperatura promedio de la Tierra es el tema de mucha discusión actual. La Tierra está en contacto radiactivo tanto con el Sol como con el espacio oscuro, por lo que no podemos usar la ecuación para un ambiente a una temperatura uniforme. La Tierra recibe casi toda su energía de la radiación del Sol y refleja parte de ella en el espacio exterior. Por el contrario, el espacio oscuro es muy frío, alrededor de $3 K$, por lo que la Tierra irradia energía hacia el cielo oscuro. La tasa de transferencia de calor del suelo y las hierbas puede ser tan rápida que las heladas pueden ocurrir en las tardes de verano, incluso en latitudes cálidas.
La temperatura promedio de la Tierra está determinada por su balance de energía. Para una primera aproximación, es la temperatura a la cual la Tierra irradia calor al espacio tan rápido como recibe energía del Sol.
Un parámetro importante en el cálculo de la temperatura de la Tierra es su emisividad ($e$). En promedio, es aproximadamente $0,65$, pero el cálculo de este valor se complica por la gran variación diaria en la cobertura de nubes altamente reflectante.
Debido a que las nubes tienen menor emisividad que los océanos o masas terrestres, reflejan parte de la radiación hacia la superficie, reduciendo en gran medida la transferencia de calor al espacio oscuro, así como reducen en gran medida la transferencia de calor a la atmósfera durante el día. Hay comentarios negativos (en los que un cambio produce un efecto que se opone a ese cambio) entre las nubes y la transferencia de calor; las temperaturas más altas evaporan más agua para formar más nubes, que reflejan una mayor radiación hacia el espacio, reduciendo la temperatura.
El efecto invernadero frecuentemente mencionado está directamente relacionado con la variación de la emisividad de la Tierra con la longitud de onda (). El efecto invernadero es un fenómeno natural responsable de proporcionar temperaturas adecuadas para la vida en la Tierra y para hacer que Venus no sea apto para la vida humana. La mayor parte de la radiación infrarroja emitida desde la Tierra es absorbida por el dióxido de carbono ($CO_2$) y el agua ($H_2O$) en la atmósfera y luego re-irradiada al espacio exterior o de regreso a la Tierra. La re-radiación de vuelta a la Tierra mantiene su temperatura superficial alrededor de $40 °C$ más alta de lo que sería si no hubiera atmósfera (Las paredes de vidrio y el techo de un invernadero aumentan la temperatura interior al bloquear las pérdidas de calor por convección, no las pérdidas por radiación).
El efecto invernadero es fundamental para la discusión del calentamiento global debido a la emisión de dióxido de carbono y metano (y otros gases de efecto invernadero) a la atmósfera terrestre procedentes de la industria, el transporte y la agricultura. Los cambios en el clima mundial podrían provocar tormentas más intensas, cambios en las precipitaciones (que afectan a la agricultura), reducción de la biodiversidad de la selva tropical y aumento del nivel del mar.
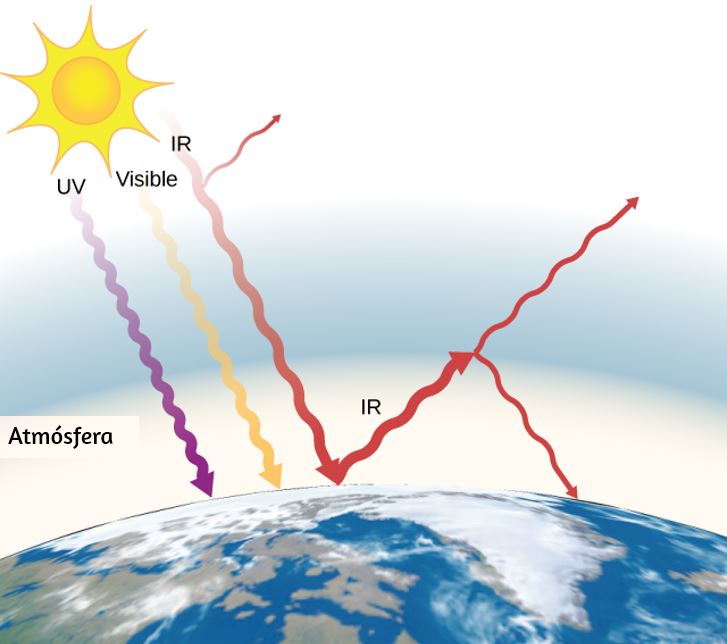
Estrategia de resolución de problemas: efectos de la transferencia de calor
1. Examina la situación para determinar qué tipo de transferencia de calor está involucrado.
2. Identifica los tipos de transferencia de calor: conducción, convección o radiación.
3. Identifica exactamente qué debe determinarse en el problema (identifica las incógnitas). Una lista escrita es útil.
4. Haz una lista de lo que se da o lo que se puede inferir del problema tal como se establece (identifique los datos conocidos).
5. Resuelve la ecuación apropiada para la cantidad que se determinará (la incognita).
6. Para la conducción, use la ecuación $P = kAΔT/d$. La enumera las conductividades térmicas. Para la convección, determina la cantidad de materia movida y la ecuación $Q = mcΔT$, junto con $Q = mL_f$ o $Q = mL_v$ si una sustancia cambia de fase. Para la radiación, la ecuación $P_{\textsf{neta}} = σeA (T_2^4 - T_1^4)$ proporciona la tasa de transferencia de calor neta.
7. Sustituye los datos conocidos junto con sus unidades en la ecuación apropiada y obtén soluciones numéricas completas con unidades.
8. Verifica la respuesta para ver si es razonable. ¿Tiene sentido?
 Comprueba tu aprendizaje 1.9
Comprueba tu aprendizaje 1.9
Las siguientes escenas interactivas hacen parte del proyecto @prende.mx, dirigido por el Dr. José Luis Abreu León
La luz del Sol y la de una lámpara son ejemplos de radiación. Cuando la radiación incide en un cuerpo, éste la absorbe y se calienta, es decir, aumenta su temperatura. No toda la radiación es luz visible. Cuando nos acercamos a un cuerpo muy caliente, aún sin tocarlo sentimos su calor. Observa algunos ejemplos de transmisión del calor por radiación.
¿Qué efecto tiene la radiación en la temperatura?, ¿Cuáles cuerpos emiten y cuáles absorben radiación? En esta escena explorarás el efecto de la radiación en los cuerpos y verás que cuando un cuerpo absorbe radiación, aumenta su temperatura y que un cuerpo caliente emite radiación y eso lo lleva a enfriarse. Los cuerpos que absorben y emiten bien la radiación son los que no brillan y tienen colores obscuros. Aquí a tales cuerpos les llamamos opacos. Los cuerpos que ni absorben ni emiten bien la radiación son los que son brillantes y de colores claros. Aquí a tales cuerpos les llamamos reflejantes.
 Comprueba tu aprendizaje - Test de Falso y Verdadero
Comprueba tu aprendizaje - Test de Falso y Verdadero
 Comprueba tu aprendizaje - Test de Falso y Verdadero
Comprueba tu aprendizaje - Test de Falso y Verdadero

Los gases están literalmente a nuestro alrededor: el aire que respiramos es una mezcla de gases. Otros gases incluyen los que hacen que los panes y las tortas sean blandos, los que hacen que las bebidas sean gaseosas, y los que se queman para calentar muchas casas. Los motores y los refrigeradores dependen del comportamiento de los gases, como veremos en capítulos posteriores.
Como discutimos en el capítulo anterior, el estudio del calor y la temperatura es parte de un área de la física conocida como termodinámica, en la que se requiere que un sistema sea macroscópico, es decir, que consista en un gran número de moléculas (como $10^{23}$). Comenzaremos considerando algunas propiedades macroscópicas de los gases: volumen, presión y temperatura. El modelo simple de un hipotético "gas ideal" describe estas propiedades de un gas con mucha precisión bajo muchas condiciones. Pasaremos del modelo de gas ideal a una aproximación más ampliamente aplicable, llamada modelo de Van der Waals.
Para comprender los gases aún mejor, también debemos mirarlos en la escala microscópica de las moléculas. En los gases, las moléculas interactúan débilmente, por lo que el comportamiento microscópico de los gases es relativamente simple y sirven como una buena introducción a los sistemas de muchas moléculas. El modelo molecular de los gases se llama la teoría cinética de los gases y es uno de los ejemplos clásicos de un modelo molecular que explica el comportamiento cotidiano.
En esta sección, exploraremos el comportamiento térmico de los gases. Nuestra palabra "gas" proviene de la palabra flamenca que significa "caos", utilizada por primera vez para los vapores por el químico J. B. van Helmont, del siglo XVII. El término era más apropiado de lo que él sabía, porque los gases consisten en moléculas que se mueven y colisionan entre sí al azar. Esta aleatoriedad hace que la conexión entre los dominios microscópico y macroscópico sea más simple para los gases que para los líquidos o sólidos.
¿Cómo se diferencian los gases de los sólidos y líquidos? En condiciones normales, como las del aire que nos rodea, la diferencia es que las moléculas de los gases están mucho más separadas que las de los sólidos y líquidos. Debido a que las distancias típicas entre las moléculas son grandes en comparación con el tamaño de una molécula, como se ilustra en la , las fuerzas entre ellas se consideran insignificantes, excepto cuando entran en contacto entre sí durante las colisiones. Además, a temperaturas muy superiores a la temperatura de ebullición, el movimiento de las moléculas es rápido y los gases se expanden rápidamente para ocupar todo el volumen accesible. Por el contrario, en líquidos y sólidos, las moléculas están más juntas, y el comportamiento de las moléculas en líquidos y sólidos está muy restringido por las interacciones de las moléculas entre sí. Las propiedades macroscópicas de tales sustancias dependen fuertemente de las fuerzas entre las moléculas, y dado que muchas moléculas están interactuando, los "problemas de muchos cuerpos" resultantes pueden ser extremadamente complicados.
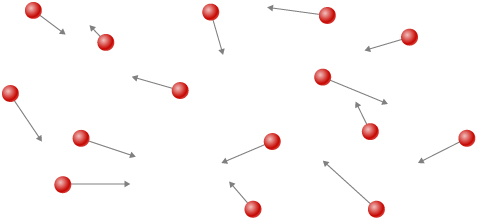
La siguiente escena interactiva, diseñada por Andrew Duffy, se puede encontrar en la colección de http://physics.bu.edu/~duffy/classroom.html
En el capítulo anterior, vimos una consecuencia del gran espaciado intermolecular en los gases: los gases se comprimen fácilmente. La muestra que los gases tienen mayores coeficientes de expansión de volumen que los sólidos o líquidos. Estos grandes coeficientes significan que los gases se expanden y contraen muy rápidamente con los cambios de temperatura. También vimos (en la sección de expansión térmica) que la mayoría de los gases se expanden a la misma velocidad o tienen el mismo coeficiente de expansión de volumen, $β$. Esto plantea una pregunta: ¿por qué todos los gases actúan casi de la misma manera, cuando todos los diversos líquidos y sólidos tienen tasas de expansión muy variables?
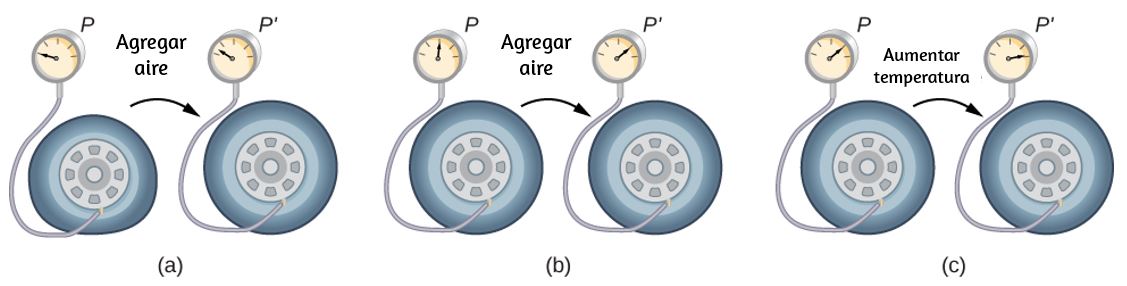
Para estudiar cómo se relacionan la presión, la temperatura y el volumen de un gas, ten en cuenta lo que sucede cuando bombeas aire a un neumático desinflado (). El volumen del neumático primero aumenta en proporción directa a la cantidad de aire inyectado, sin mucho aumento en la presión del neumático.
Una vez que el neumático se ha expandido a casi su tamaño completo, las paredes del neumático limitan su expansión de volumen. Si continuamos bombeando aire dentro del neumático, la presión aumenta. Cuando se conduce el automóvil y las llantas se flexionan, su temperatura aumenta y, por lo tanto, la presión aumenta aún más.
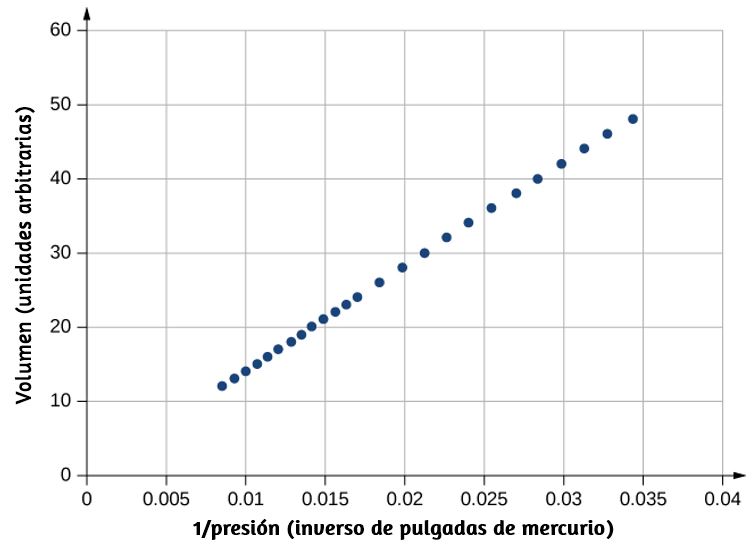
La muestra datos de los experimentos de Robert Boyle (1627-1691), que ilustran lo que ahora se llama la ley de Boyle: a temperatura constante y número de moléculas, la presión absoluta de un gas y su volumen son inversamente proporcionales. (Recuerda por Mecánica de Fluidos que la presión absoluta es la verdadera presión y la presión manométrica es la presión absoluta menos la presión ambiente, típicamente la presión atmosférica). El gráfico de la muestra esta relación como una proporcionalidad inversa de volumen a presión.
La muestra datos experimentales que ilustran lo que se conoce como la ley de Charles, creada por Jacques Charles (1746-1823). La ley de Charles establece que a presión constante y número de moléculas, el volumen de un gas es proporcional a su temperatura absoluta.
Similar es la ley de Amonton o ley de Gay-Lussac, que establece que a un volumen y cantidad constante de moléculas, la presión es proporcional a la temperatura. Esa ley es la base del termómetro de gas de volumen constante, discutido en el capítulo anterior (Las historias de estas leyes y el crédito apropiado para ellas son más complicadas de lo que se puede discutir aquí).
Se sabe experimentalmente que para los gases a baja densidad (de modo que sus moléculas ocupan una fracción insignificante del volumen total) y a temperaturas muy superiores al punto de ebullición, estas proporciones se mantienen en una buena aproximación. No es de sorprender que, con las otras cantidades mantenidas constantes, la presión o el volumen sean proporcionales al número de moléculas. Más sorprendentemente, cuando las proporcionalidades se combinan en una sola ecuación, la constante de proporcionalidad es independiente de la composición del gas. La ecuación resultante para todos los gases se aplica en el límite de baja densidad y alta temperatura; es lo mismo para el oxígeno que para el helio o el hexafluoruro de uranio.
Un gas en ese límite se llama un gas ideal; obedece a la ley de los gases ideales, que también se llama ecuación de estado de un gas ideal.
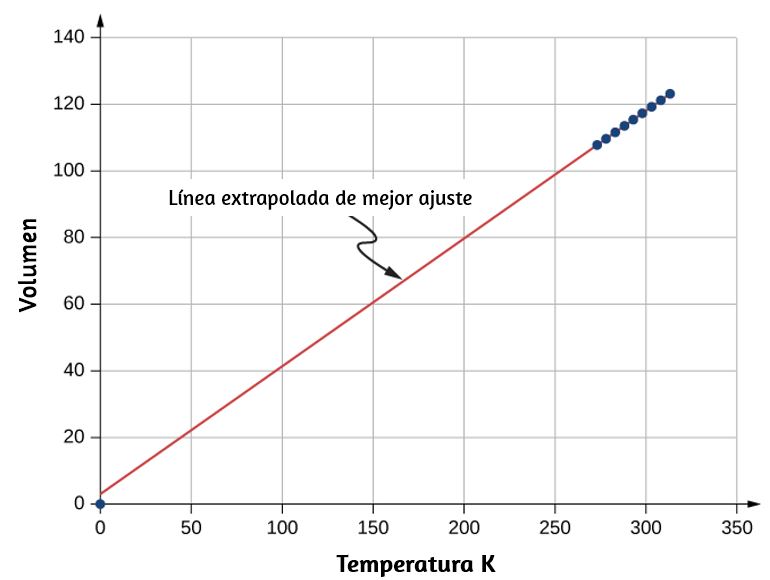
Ley de los gases ideales
La ley de los gases ideales establece que
$$pV = Nk_BT \tag{2.1}$$donde $p$ es la presión absoluta de un gas, $V$ es el volumen que ocupa, $N$ es el número de moléculas en el gas y $T$ es su temperatura absoluta.
La constante $k_B$ se llama la constante de Boltzmann en honor del físico austríaco Ludwig Boltzmann (1844-1906) y tiene el valor
$$k_B = 1,38 × 10^{-23} J/K$$La ley de los gases ideales describe el comportamiento de cualquier gas real cuando su densidad es lo suficientemente baja o su temperatura lo suficientemente alta como para estar lejos de la licuefacción. Esto abarca muchas situaciones prácticas. En la siguiente sección, veremos por qué es independiente del tipo de gas.
En muchas situaciones, la ley de los gases ideales se aplica a una muestra de gas con un número constante de moléculas; por ejemplo, el gas puede estar en un contenedor sellado. Si $N$ es constante, resolver para $N$ muestra que $pV/T$ es constante. Podemos escribir ese hecho en una forma conveniente:
En la ecuación anterior, los subíndices 1 y 2 se refieren a cualesquiera dos estados del gas en diferentes momentos. De nuevo, la temperatura debe expresarse en kelvin y la presión debe ser absoluta, que es la suma de la presión manométrica y la presión atmosférica.
Ejemplo 2.1
Cálculo de los cambios de presión debido a los cambios de temperatura
Supongamos que el neumático de tu bicicleta está completamente inflado, con una presión absoluta de $7.00 × 10^5 Pa$ (una presión manométrica de poco menos de $90.0 lb/in^2$) a una temperatura de $18.0 °C$.
¿Cuál es la presión después de que su temperatura ha subido a $35.0 °C$ en un día caluroso? Supón que no hay fugas apreciables o cambios en el volumen.
Estrategia
La presión en el neumático está cambiando solo debido a los cambios de temperatura. Sabemos que la presión inicial $p_0 = 7.00 × 10^5 Pa$, la temperatura inicial $T_0 = 18.0 °C$, y la temperatura final $T_f = 35.0 °C$. Debemos encontrar la presión final $p_f$. Dado que el número de moléculas es constante, podemos usar la ecuación
$$\frac{p_fV_f}{T_f} = \frac{p_0V_0}{T_0}$$Como el volumen es constante, $V_f$ y $V_0$ son iguales. Por lo tanto,
$$\frac{p_f}{T_f} = \frac{p_0}{T_0}$$Podemos reorganizar esto para hallar $p_f$:
$$p_f = p_0\frac{T_f}{T_0}$$donde la temperatura debe estar en Kelvin.
Solución
1. Convierte las temperaturas de grados Celsius a Kelvin
$$T_0 = (18.0 + 273) K = 291 K,$$ $$T_f = (35.0 + 273) K = 30 8K$$2. Sustituye los valores conocidos en la ecuación,
$$p_f = p_0\frac{T_f}{T_0} = 7.00 × 10^5 Pa(\frac{308 K}{291 K}) = 7.41 × 10^5 Pa$$Explicación
La temperatura final es aproximadamente un $6$% mayor que la temperatura original, por lo que la presión final es aproximadamente un $6$% mayor también. Ten en cuenta que la presión absoluta (consulta Mecánica de fluidos) y la temperatura absoluta (consulta Temperatura y calor) deben utilizarse en la ley de gases ideales.
Ejemplo 2.2
Cálculo del número de moléculas en un metro cúbico de gas
¿Cuántas moléculas hay en un objeto típico, como gas en un neumático o agua en un vaso? Este cálculo nos puede dar una idea de cuán grande es típicamente $N$. Calculemos el número de moléculas en el aire que un adulto joven sano inhala en una respiración, con un volumen de $500 ml$, a temperatura y presión estándar (STP), que se define como $0 °C$ y presión atmosférica (Nuestro joven adulto aparentemente está afuera en invierno).
Estrategia
Debido a que se especifican la presión, el volumen y la temperatura, podemos usar la ley de los gases ideales, $pV = Nk_BT$, para encontrar $N$.
Solución
1. Identifica los datos conocidos.
$T = 0 °C = 273 K$, $p = 1.01 × 10^5 Pa$, $V = 500 mL = 5 × 10^{-4} m^3$, $k_B = 1.38 × 10^{-23} J/K$
2. Sustituye los valores conocidos en la ecuación y halla $N$.
$$N = \frac{pV}{k_BT} = \frac{(1.01 × 10^5 Pa)(5 × 10^{-4} m^3)}{(1.38 × 10^{-23} J/K)(273 K)} = 1.34 × 10^{22} moléculas$$Explicación
$N$ es enorme, incluso en pequeños volúmenes. Por ejemplo, $1 cm^3$ de un gas en STP contiene $2,68 × 10^{19}$ moléculas. Una vez más, ten en cuenta que nuestro resultado para $N$ es el mismo para todos los tipos de gases, incluidas las mezclas.
Según la mecánica de fluidos, los pascales son $N/m^2$, entonces $Pa \cdot m^3 = N \cdot m = J$. Por lo tanto, nuestro resultado para $N$ es adimensional, un número puro que podría obtenerse contando (en principio) en lugar de medir. Como es el número de moléculas, ponemos "moléculas" después del número, teniendo en cuenta que es una ayuda para la comunicación en lugar de una unidad.
A menudo es conveniente medir la cantidad de sustancia con una unidad en una escala más humana que las moléculas. La unidad del SI para este fin fue desarrollada por el científico italiano Amedeo Avogadro (1776-1856). (Trabajó a partir de la hipótesis de que volúmenes iguales de gas a igual presión y temperatura contienen el mismo número de moléculas, independientemente del tipo de gas. Como se mencionó anteriormente, esta hipótesis se ha confirmado cuando se aplica la aproximación del gas ideal).
Una mole (abreviada mol) se define como la cantidad de cualquier sustancia que contiene tantas moléculas como átomos hay en exactamente $12$ gramos ($0.012 kg$) de carbono 12. (Técnicamente, deberíamos decir "unidades de fórmula", no "moléculas", pero esta distinción es irrelevante para nuestros propósitos). El número de moléculas en una mole se llama número de Avogadro ($N_A$), y ahora se conoce el valor del número de Avogadro. Así
$$N_A = 6.02 × 10^{23} mol^{-1}$$Ahora podemos escribir $N = N_An$, donde $n$ representa el número de moles de una sustancia.
El número de Avogadro relaciona la masa de una cantidad de sustancia en gramos con la cantidad de protones y neutrones en un átomo o molécula (12 para un átomo de carbono 12), que aproximadamente determinan su masa. Es natural definir una unidad de masa tal que la masa de un átomo sea aproximadamente igual a su número de neutrones y protones. La unidad de ese tipo aceptada para su uso con el SI es la unidad de masa atómica unificada ($u$), también llamada Dalton. Específicamente, un átomo de carbono 12 tiene una masa de exactamente $12 u$, de modo que su masa molar $M$ en gramos por mol es numéricamente igual a la masa de un átomo de carbono-12 en $u$. Esa igualdad es válida para cualquier sustancia. En otras palabras, $N_A$ no es solo la conversión de números de moléculas a moles, sino que también es la conversión de $u$ a gramos: $6.02 × 10^{23} u = 1g$. ().
Ahora, dejando que $m_s$ represente la masa de una muestra de una sustancia, tenemos $m_s = nM$. Si dejamos que m represente la masa de una molécula, tenemos $M = N_Am$.
 Comprueba tu aprendizaje 2.1
Comprueba tu aprendizaje 2.1
 Comprueba tu aprendizaje 2.2
Comprueba tu aprendizaje 2.2
Una expresión muy común de la ley de los gases ideales usa la cantidad de moles en una muestra, $n$, en lugar de la cantidad de moléculas, $N$. Partimos de la ley de los gases ideales,
$$pV = Nk_BT$$multiplicando y dividiendo el lado derecho de la ecuación por el número $N_A$ de Avogadro. Esto nos da
$$pV = \frac{N}{N_A}N_Ak_BT$$Ten en cuenta que $n = N/NA$ es la cantidad de moles. Definimos la constante de gas universal como $R = N_Ak_B$, y obtenemos la ley de los gases ideales en términos de moles.
Ley de los gases ideales (en términos de moles)
En términos de número de moles $n$, la ley de los gases ideales se escribe como
$$pV = nRT \tag{2.3}$$Las unidades en el SI, serían:
$$R = N_Ak_B = (6.02 × 10^{23} mol^{-1})\left(1.38 × 10^{-23} \frac{J}{K} \right) = 8.31 \frac{J}{mol \cdot K}$$En otras unidades
$$R = 1.99 \frac{cal}{mol \cdot K} = 0.0821 \frac{L \cdot atm}{mol \cdot K}$$Puedes usar el valor de $R$ que sea más conveniente para un problema en particular.
Ejemplo 2.3
Densidad del aire en STP y en un globo de aire caliente
Calcula la densidad del aire seco (a) en condiciones estándar y (b) en un globo de aire caliente a una temperatura de $120 °C$. El aire seco es aproximadamente $78$% de $N_2$, $21$% de $O_2$ y $1$% de $A_r$.
Estrategia y solución
a. Se nos pide que encontremos la densidad, o masa por metro cúbico. Podemos comenzar encontrando la masa molar. Si tenemos cien moléculas, de las cuales 78 son nitrógeno, 21 son oxígeno y 1 es argón, la masa molecular promedio es ($78 m_{N_2} + 21m_{O_2} + m_{Ar})/100$, o la masa de cada componente se multiplica por su porcentaje. Lo mismo se aplica a la masa molar, que por lo tanto es
$$M = 0.78M_{N_2} + 0.21M_{O_2} + 0.01M_{Ar} = 29.0 g/mol$$Ahora podemos encontrar la cantidad de moles por metro cúbico. Usamos la ley de los gases ideales en términos de moles, $pV = nRT,$ con $p = 1.00 atm$, $T = 273 K$, $V = 1m^3$ y $R = 8.31 J/mol \cdot K.$ La opción más conveniente para $R$ en este caso es $R = 8.31 J/mol \cdot K$ porque los datos conocidos están en unidades del SI:
Entonces, la masa $m_s$ de este aire es
$$m_s = nM = (44.5 mol)(29.0 g/mol) = 1290 g = 1.29kg$$Finalmente, la densidad del aire en STP es
$$ρ = \frac{m_s}{V} = \frac{1.29kg}{1 m^3} = 1.29 kg/m^3$$b. La presión de aire dentro del globo todavía es de $1 atm$ porque la parte inferior del globo está abierta a la atmósfera. El cálculo es el mismo excepto que usamos una temperatura de $120 °C$, que es $393 K$. Podemos repetir el cálculo en (a), o simplemente observar que la densidad es proporcional al número de moles, que es inversamente proporcional a la temperatura. Luego, usando los subíndices 1 para aire en STP y 2 para el aire caliente, tenemos
$$ρ_2 = \frac{T_1}{T_2}ρ_1 = \frac{273 K}{393 K}(1.29 kg/m^3) = 0.896 kg/m^3$$Explicación
Utilizando los métodos del Principio de la Flotabilidad de Arquímedes, podemos encontrar que la fuerza neta en $2200 m^3$ de aire a $120 °C$ es $F_b - F_g = ρ_{\textsf{atmósfera}}V_g - ρ_{\textsf{aire caliente}}V_g = 8.49 × 10^3 N$, o lo suficiente para levantar unos $867 kg$. La densidad de masa y la densidad molar del aire en STP, que se encuentran arriba, son a menudo números útiles. A partir de la densidad molar, podemos determinar fácilmente otro número útil, el volumen de un mol de cualquier gas ideal en STP, que es $22.4 L$.
 Comprueba tu aprendizaje 2.3
Comprueba tu aprendizaje 2.3
La ley de los gases ideales está estrechamente relacionada con la energía: las unidades en ambos lados de la ecuación son joules. El lado derecho de la ecuación de ley de gas ideal es $Nk_BT$. Este término es aproximadamente la energía cinética de traslación total (que, cuando se habla de gases, se refiere a la energía de la traslación de una molécula, no la de la vibración de sus átomos o rotación) de $N$ moléculas a una temperatura absoluta $T$, como veremos formalmente en la siguiente sección.
El lado izquierdo de la ecuación de ley de gas ideal es $pV$. Como se menciona en el ejemplo sobre el número de moléculas en un gas ideal, la presión multiplicada por el volumen tiene unidades de energía. La energía de un gas puede cambiarse cuando el gas funciona ya que aumenta en volumen, algo que exploramos en el capítulo anterior, y la cantidad de trabajo está relacionada con la presión. Este es el proceso que ocurre en motores de gasolina o de vapor y turbinas, como veremos en el próximo capítulo.
Estrategia de resolución de problemas: la ley de los gases ideales
Paso 1. Examina la situación para determinar si se trata de un gas ideal. La mayoría de los gases son casi ideales a menos que estén cerca del punto de ebullición o a presiones muy por encima de la presión atmosférica.
Paso 2. Haz una lista de las cantidades que se dan o se pueden inferir del problema tal como se establece (identifica las cantidades conocidas).
Paso 3. Identifica exactamente qué debe determinarse en el problema (identifica las incógnitas). Una lista escrita es útil.
Paso 4. Determina si se sabe o se debe saber el número de moléculas o la cantidad de moles para decidir si se usa la ley de los gases ideales como $pV = Nk_BT$, donde $N$ es el número de moléculas, o $pV = nRT$, donde $n$ es el cantidad de moles
Paso 5. Convierte los valores conocidos en unidades del SI adecuadas ($K$ para temperatura, $Pa$ para presión, $m^3$ para volumen, moléculas para $N$ y moles para $n$). Si las unidades de los datos conocidos son consistentes con uno de los valores de $R$ que no son SI, puedes dejarlos en esas unidades.
Paso 6. Desarrolla la ley de los gases ideales para la cantidad que se determinará (la cantidad desconocida). Es posible que debas tomar una proporción de estados finales a estados iniciales para eliminar las cantidades desconocidas que se mantienen fijas.
Paso 7. Sustituye las cantidades conocidas, junto con sus unidades, en la ecuación apropiada y obtén soluciones numéricas completas con unidades.
Paso 8. Verifica la respuesta para ver si es razonable: ¿tiene sentido?
Hemos observado repetidamente que la ley de los gases ideales es una aproximación. ¿Cómo se puede mejorar? La ecuación de estado de van der Waals (llamada así por el físico holandés Johannes van der Waals, 1837-1923) la mejora al tomar en cuenta dos factores. Primero, las fuerzas de atracción entre las moléculas, que son más fuertes a mayor densidad y reducen la presión, se toman en cuenta al agregar a la presión un término igual al cuadrado de la densidad molar multiplicado por un coeficiente positivo $a$. En segundo lugar, el volumen de las moléculas está representado por una constante positiva $b$, que puede considerarse como el volumen de una mol de moléculas. Esto se resta del volumen total para dar el volumen restante en el que las moléculas pueden moverse. Las constantes a y b se determinan experimentalmente para cada gas. La ecuación resultante es
En el límite de baja densidad ($n$ pequeño), los términos $a$ y $b$ son insignificantes, y tenemos la ley de los gases ideales, como deberíamos para la baja densidad. Por otro lado, si $V - nb$ es pequeño, lo que significa que las moléculas están muy juntas, la presión debe ser más alta para dar el mismo $nRT$, como se esperaría en la situación de un gas altamente comprimido. Sin embargo, el aumento en la presión es menor de lo que sugeriría ese argumento, porque a una densidad alta el término $(n/V)^2$ es significativo. Como es positivo, causa una menor presión para dar el mismo $nRT$.
La ecuación de estado de van der Waals funciona bien para la mayoría de los gases en una amplia variedad de condiciones. Como veremos en el siguiente módulo, incluso predice la transición gas-líquido.
Podemos examinar aspectos del comportamiento de una sustancia trazando un diagrama $pV$, que es un gráfico de presión versus volumen. Cuando la sustancia se comporta como un gas ideal, la ley de los gases ideales $pV = nRT$, describe la relación entre su presión y su volumen. En un diagrama $pV$, es común trazar una isoterma, que es una curva que muestra $p$ como una función de $V$ con el número de moléculas y la temperatura fija. Entonces, para un gas ideal, $pV = constante$, por ejemplo, el volumen del gas disminuye a medida que aumenta la presión. El gráfico resultante es una hipérbola. Sin embargo, si asumimos la ecuación de estado de van der Waals, las isotermas se vuelven más interesantes, como se muestra en la .
A altas temperaturas, las curvas son aproximadamente hipérbolas, lo que representa un comportamiento aproximadamente ideal a varias temperaturas fijas. A temperaturas más bajas, las curvas se parecen cada vez menos a hipérbolas; es decir, el gas no se comporta de manera ideal. Hay una temperatura crítica T_c en la que la curva tiene un punto con pendiente cero. Por debajo de esa temperatura, las curvas no disminuyen monótonamente; en cambio, cada uno tiene una "joroba", lo que significa que para un cierto rango de volumen, aumentar el volumen aumenta la presión.
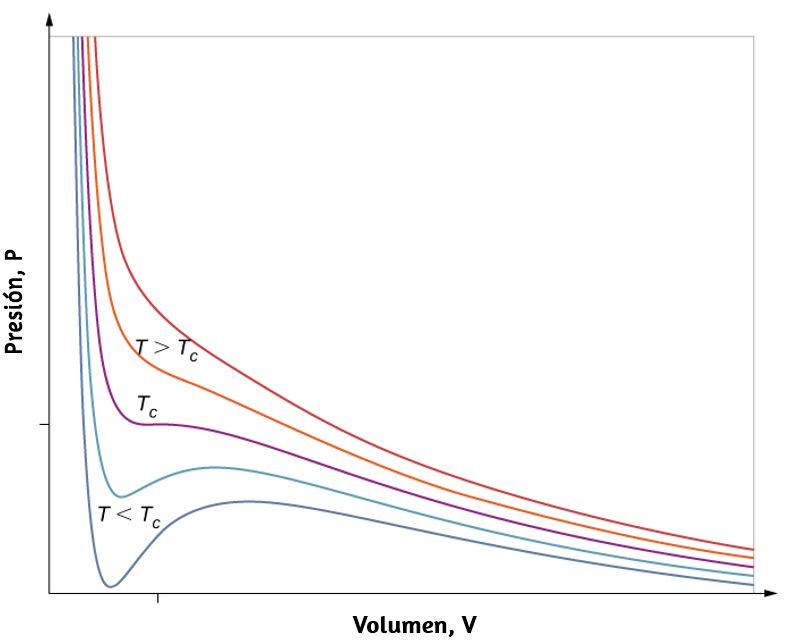
Tal comportamiento sería completamente no físico. En cambio, se entiende que las curvas describen una transición de fase líquido-gas. La parte oscilante de la curva se reemplaza por una línea horizontal, que muestra que a medida que el volumen aumenta a temperatura constante, la presión se mantiene constante. Ese comportamiento corresponde a la ebullición y a la condensación; cuando una sustancia está a su temperatura de ebullición para una presión particular, puede aumentar de volumen a medida que parte del líquido se convierte en gas o disminuye a medida que parte del gas se convierte en líquido, sin ningún cambio en la temperatura o la presión.
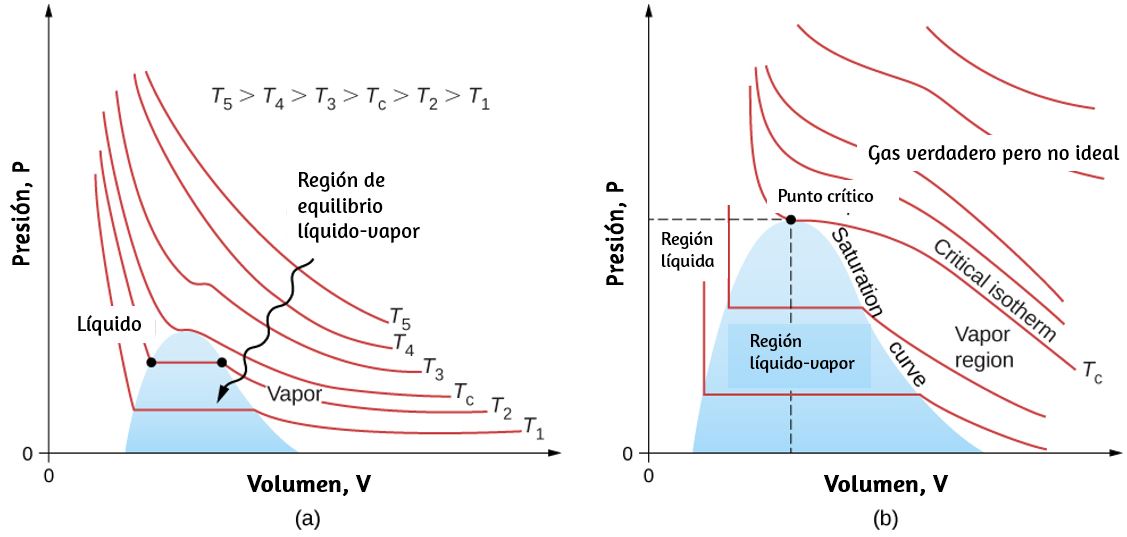
muestra isotermas similares que son más realistas que las basadas en la ecuación de van der Waals. Las partes empinadas de las curvas a la izquierda de la región de transición muestran la fase líquida, que es casi incompresible: una ligera disminución en el volumen requiere un gran aumento en la presión. Las partes planas muestran la transición líquido-gas; las regiones azules que definen representan combinaciones de presión y volumen donde el líquido y el gas pueden coexistir.
Las isotermas superiores a $T_c$ no pasan por la transición de gas líquido. Por lo tanto, el líquido no puede existir por encima de esa temperatura, que es la temperatura crítica (que se describe en el capítulo sobre temperatura y calor). A una presión suficientemente baja por encima de esa temperatura, el gas tiene la densidad de un líquido pero no se condensa; el gas se dice que es supercrítico. A mayor presión, es sólido.
El dióxido de carbono, por ejemplo, no tiene fase líquida a una temperatura superior a $31,0 °C$. La presión crítica es la presión máxima a la que puede existir el líquido. El punto en el diagrama $pV$ a la presión y temperatura críticas es el punto crítico (que aprendiste en el capítulo sobre temperatura y calor). La enumera las temperaturas y presiones críticas representativas.
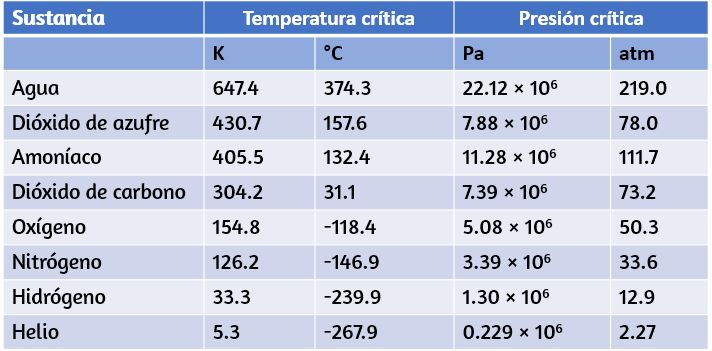
A continuación, presentamos una escena interactiva publicada en la Red Descartes. Este tipo de escena interactiva está concebida de tal forma que el alumno descubra por sí mismo las características esenciales de los conceptos estudiados, en nuestro caso las leyes de los gases ideales. El diseño del contenido y programación fue realizado por Tine Stalmans (LITE), José Luis Abreu León, Instituto de Matemáticas (UNAM) y Carlos Jaimes Alberto Vergara.
A través de una conversación con un tutor digital y la observación y/o manipulación simultánea de modelos interactivos, analizarás, tanto a nivel macro como submicroscópico, el comportamiento de un gas que está siendo comprimido dentro de un cilindro con un émbolo. Esto te permitirá conocer y entender la ley general de los gases, y las leyes de Boyle y Gay-Lussac en particular.
El diálogo se desarrollará a través de los siguientes puntos clave:
Hemos examinado la presión y la temperatura en función de sus definiciones macroscópicas. La presión es la fuerza dividida por el área sobre la que se ejerce la fuerza, y la temperatura se mide con un termómetro. Podemos obtener una mejor comprensión de la presión y la temperatura a partir de la teoría cinética de los gases, la teoría que relaciona las propiedades macroscópicas de los gases con el movimiento de las moléculas de las que están compuestos. Primero, hacemos dos suposiciones sobre las moléculas en un gas ideal.
Para derivar la ley del gas ideal y la conexión entre cantidades microscópicas como la energía de una molécula típica y cantidades macroscópicas como la temperatura, analizamos una muestra de un gas ideal en un contenedor rígido, sobre el cual hacemos dos suposiciones más:
Las colisiones entre moléculas no aparecen en la derivación de la ley de los gases ideales. Tampoco perturban la derivación, ya que las colisiones entre moléculas que se mueven con velocidades aleatorias dan nuevas velocidades aleatorias. Además, si las velocidades de las moléculas de gas en un contenedor inicialmente no son aleatorias e isótropas, las colisiones moleculares son las que las hacen aleatorias e isótropas.
Hacemos más suposiciones que simplifican los cálculos pero no afectan el resultado. Primero, dejamos que el contenedor sea una caja rectangular. En segundo lugar, comenzamos considerando los gases monoatómicos, aquellos cuyas moléculas consisten en átomos individuales, como el helio. Entonces, podemos suponer que los átomos no tienen energía, excepto su energía cinética de traslación; por ejemplo, no tienen energía rotacional ni vibratoria.
Más tarde, discutimos la validez de esta suposición para los gases monoatómicos reales y prescindimos de ella para considerar los gases diatómicos y poliatómicos.
La muestra una colisión de una molécula de gas con la pared de un contenedor, de modo que ejerce una fuerza sobre la pared (según la tercera ley de Newton). Estas colisiones son la fuente de presión en un gas. A medida que aumenta el número de moléculas, aumenta el número de colisiones y, por lo tanto, la presión. De manera similar, si la velocidad promedio de las moléculas es mayor, la presión del gas es mayor.
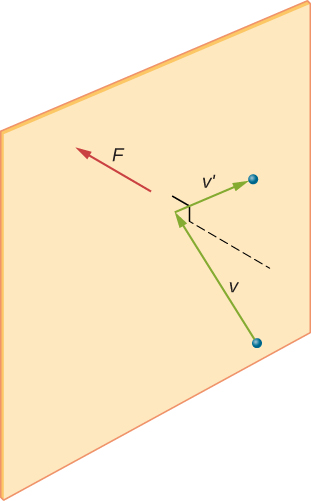
En una muestra de gas en un contenedor, la aleatoriedad del movimiento molecular hace que el número de colisiones de moléculas con cualquier parte de la pared fluctúe en un momento dado. Sin embargo, debido a que un gran número de moléculas colisionan con la pared en poco tiempo, el número de colisiones en las escalas de tiempo y espacio que medimos fluctúa solo por una fracción pequeña, generalmente no observable, del promedio.
Podemos comparar esta situación con la de un casino, donde los resultados de las apuestas son aleatorios y las tomas del casino fluctúan por minuto y por hora. Sin embargo, durante largos períodos como un año, las ganancias del casino están muy cerca de los promedios esperados. Un tanque de gas tiene muchísimas más moléculas de las que un casino tiene apostadores en un año, y las moléculas hacen colisiones enormemente más en un segundo que las apuestas que tiene un casino.
Un cálculo de la fuerza promedio ejercida por las moléculas en las paredes de la caja nos lleva a la ley de los gases ideales y a la conexión entre la temperatura y la energía cinética molecular (de hecho, tomaremos dos promedios: uno a lo largo del tiempo para obtener la fuerza promedio ejercida por una molécula con una velocidad determinada, y luego otra media sobre las moléculas con diferentes velocidades). Este enfoque fue desarrollado por Daniel Bernoulli (1700-1782) , que es mejor conocido en física por su trabajo en el flujo de fluidos (hidrodinámica). Sorprendentemente, Bernoulli hizo este trabajo antes de que Dalton estableciera la visión de la materia como compuesta de átomos.
La muestra un contenedor lleno de gas y una vista ampliada de una colisión elástica de una molécula de gas con una pared del contenedor, dividida en componentes. Hemos supuesto que una molécula es pequeña en comparación con la separación de moléculas en el gas, y que su interacción con otras moléculas puede ignorarse.
Bajo estas condiciones, la ley de los gases ideales es experimentalmente válida. Debido a que también hemos asumido que la pared es rígida y las partículas son puntos, la colisión es elástica. Por lo tanto, la energía cinética de la molécula permanece constante, y por lo tanto, su velocidad y la magnitud de su momento también permanecen constantes. Esta suposición no siempre es válida, pero los resultados en el resto de este módulo también se obtienen en modelos que permiten a las moléculas intercambiar energía y momento con la pared.
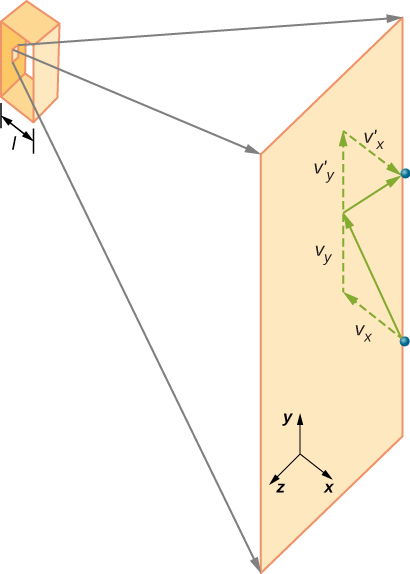
Si la velocidad de la molécula cambia en la dirección $x$, su momento cambia de $-mv_x a + mv_x$. Por lo tanto, su cambio en el momento es $Δmv = + mv_x - (- mv_x) = 2mv_x$. De acuerdo con el teorema de impulso-momento dado en el capítulo sobre el momento lineal y las colisiones, la fuerza ejercida sobre la $i$-ésima molécula, con $i$ de $1$ a $N,$ viene dada por
$$F_i = \frac{Δp_i}{Δt} = \frac{2mv_{ix}}{Δt}$$(En esta ecuación sola, p representa el momento, no la presión.) No hay fuerza entre la pared y la molécula, excepto cuando la molécula toca la pared. Durante el corto tiempo de la colisión, la fuerza entre la molécula y la pared es relativamente grande, pero esa no es la fuerza que estamos buscando. Estamos buscando la fuerza promedio, por lo que tomamos $Δt$ como el tiempo promedio entre las colisiones de la molécula dada con esta pared, que es el tiempo en el que esperamos encontrar una colisión. Si $l$ representa la longitud de la caja en la dirección $x$, entonces $Δt$ es el tiempo que la molécula tomaría para cruzar la caja y volver, una distancia de $2l$, a una velocidad de $v_x$. Por lo tanto, $Δt = 2l/v_x$, y la expresión de la fuerza se convierte en
$$\frac{2mv_{ix}}{2l/v_{ix}} = \frac{mv_{ix}^2}{l}$$Esta fuerza se debe a una molécula. Para encontrar la fuerza total en la pared, $F$, necesitamos agregar las contribuciones de todas las $N$ moléculas:
$$F = \sum_{i=1}^{N} F_i = \sum_{i=1}^{N} \frac{mv_{ix}^2}{l} = \sum_{i=1}^{N} \frac{m}{l}v_{ix}^2$$Ahora usamos la definición del promedio, que denotamos con una barra, para encontrar la fuerza:
$$F = N \frac{m}{l} \left(\frac{1}{N} \sum_{i=1}^{N} v_{ix}^2 \right) = N \frac{\={v}_x^2}{l}$$Queremos la fuerza en términos de la velocidad $v$, en lugar de la componente $x$ de la velocidad. Ten en cuenta que la velocidad total al cuadrado es la suma de los cuadrados de sus componentes, de modo que
$$\={v}^2 = \={v}_x^2 + \={v}_y^2 + \={v}_z^2$$Con el supuesto de isotropía, los tres promedios en el lado derecho son iguales, por lo que
$$\={v}^2 = 3\={v}_{ix}^2$$Sustituyendo esto en la expresión de $F$, obtenemos
$$F = N\frac{m \={v}^2}{3l}$$La presión es $F / A$, así que:
$$p = \frac{F}{A} = N\frac{m \={v}^2}{3Al} = \frac{Nm\={v}^2}{3V}$$donde usamos $V = Al$ para el volumen. Esto da un resultado importante:
La combinación de esta ecuación con $pV = Nk_BT$ da
$$\frac{1}{3}Nm \={v}^2 = Nk_BT$$Podemos obtener la energía cinética promedio de una molécula, $\frac{1}{2}m \={v}^2$, del lado izquierdo de la ecuación dividiendo $N$ y multiplicando por $3/2$.
Promedio de energía cinética por molécula
La energía cinética promedio de una molécula es directamente proporcional a su temperatura absoluta:
$$\={K} = \frac{1}{2}m\={v}^2 = \frac{3}{2}k_BT \tag{2.6}$$La ecuación $\={K} = \frac{3}{2}k_BT$ es la energía cinética promedio por molécula. Nótese en particular que nada en esta ecuación depende de la masa molecular (o de cualquier otra propiedad) del gas, la presión o cualquier otra cosa que no sea la temperatura.
Si las muestras de gas de helio y xenón, con masas moleculares muy diferentes, están a la misma temperatura, las moléculas tienen la misma energía cinética promedio.
La energía interna de un sistema termodinámico es la suma de las energías mecánicas de todas las moléculas en él. Ahora podemos dar una ecuación para la energía interna de un gas ideal monoatómico. En tal gas, la única energía de las moléculas es su energía cinética de traslación. Por lo tanto, denotando la energía interna por $E_{\textsf{int}}$, simplemente tenemos $E_{\textsf{int}} = N \={K}$, o
A menudo nos gustaría usar esta ecuación en términos de moles:
$$E_{\textsf{int}} = \frac{3}{2}nRT$$Podemos resolver $\={K} = \frac{1}{2}m \={v}^2 = \frac{3}{2}k_BT$ para una velocidad típica de una molécula en un gas ideal en términos de temperatura para determinar lo que se conoce como la velocidad media cuadrática $(rms)$ de una molécula.
Velocidad rms de una molécula
La velocidad de la raíz cuadrada-media ($rms$) de una molécula, o la raíz cuadrada del promedio del cuadrado de la velocidad $\={v}^2,$ es
$$v_{\textsf{rms}} = \sqrt{\={v}^2} = \sqrt{3k_BT/m} \tag{2.8}$$La velocidad $rms$ no es la velocidad media o la velocidad más probable de las moléculas, pero proporciona una estimación calculada fácilmente de la velocidad de las moléculas que está relacionada con su energía cinética. Nuevamente podemos escribir esta ecuación en términos de la constante de gas $R$ y la masa molar $M$ en $kg/mol$:
Hacemos una digresión por un momento para responder a una pregunta que se te puede haber ocurrido: cuando aplicamos el modelo a átomos en lugar de partículas puntuales teóricas, ¿la energía cinética de rotación cambia nuestros resultados? Para responder a esta pregunta, debemos apelar a la mecánica cuántica. En la mecánica cuántica, la energía cinética de rotación no puede asumir ningún valor; está limitado a un conjunto discreto de valores, y el valor más pequeño es inversamente proporcional a la inercia de rotación. La inercia rotacional de un átomo es pequeña porque casi toda su masa se encuentra en el núcleo, que generalmente tiene un radio inferior a $10^{-14} m$.
Por lo tanto, la energía de rotación mínima de un átomo es mucho más que $\frac{1}{2}k_BT$ para cualquier temperatura alcanzable, y la energía disponible no es suficiente para hacer que un átomo gire. Volveremos a este punto al analizar los gases diatómicos y poliatómicos en la siguiente sección.
Ejemplo 2.4
Cálculo de la energía cinética y velocidad de una molécula de gas
(a) ¿Cuál es la energía cinética promedio de una molécula de gas a $20,0 °C$ (temperatura ambiente)? (b) Encuentra la velocidad $rms$ de una molécula de nitrógeno ($N_2$) a esta temperatura.
Estrategia
(a) Lo conocido en la ecuación para la energía cinética promedio es la temperatura:
$$\={K} = \frac{3}{2}k_BT$$Antes de sustituir valores en esta ecuación, debemos convertir la temperatura dada en kelvin: $T = (20.0 + 273) K = 293 K$. Podemos encontrar la velocidad rms de una molécula de nitrógeno usando la ecuación
$$v_{\textsf{rms}} = \sqrt{\={v}^2} = \sqrt{3k_BT/m}$$pero primero debemos encontrar la masa de una molécula de nitrógeno. Obteniendo la masa molar de nitrógeno $N_2$ de la tabla periódica, encontramos
$$m = \frac{M}{N_A} = \frac{2(14.0067) × 10^{−3} kg/mol)}{6.02 × 10^{23} mol^{−1}}$$Solución
a. La temperatura sola es suficiente para nosotros para encontrar la energía cinética de traslación promedio. Sustituyendo la temperatura en la ecuación de energía cinética de traslación, obtenemos:
$$\={K} = \frac{3}{2} k_BT = \frac{3}{2} (1.38 × 10^{-23} J/K)(293 K) = 6.07 × 10^{−21} J$$b. Sustituyendo esta masa y el valor de $_B$ en la ecuación para $v_{\textsf{rms}}$
Explicación
Ten en cuenta que la energía cinética promedio de la molécula es independiente del tipo de molécula. La energía cinética de traslación promedio depende solo de la temperatura absoluta. La energía cinética es muy pequeña en comparación con las energías macroscópicas, por lo que no sentimos cuando una molécula de aire golpea nuestra piel.
Por otro lado, es mucho mayor que la diferencia típica en energía potencial gravitacional cuando una molécula se mueve desde, digamos, la parte superior hasta el fondo de una habitación, por lo que nuestro desprecio de la gravedad está justificado en situaciones típicas del mundo real. La velocidad rms de la molécula de nitrógeno es sorprendentemente grande. Estas grandes velocidades moleculares no producen movimiento macroscópico de aire, ya que las moléculas se mueven en todas las direcciones con la misma probabilidad. El camino libre medio (la distancia que una molécula mueve en promedio entre colisiones, discutido un poco más adelante en esta sección) de moléculas en el aire es muy pequeño, por lo que las moléculas se mueven rápidamente pero no llegan muy lejos en un segundo. El valor alto para la velocidad eficaz se refleja en la velocidad del sonido, que es de aproximadamente $340 m/s$ a temperatura ambiente. Cuanto mayor sea la velocidad rms de las moléculas de aire, las vibraciones de sonido más rápidas se pueden transferir a través del aire. La velocidad del sonido aumenta con la temperatura y es mayor en gases con pequeñas masas moleculares, como el helio (ver ).
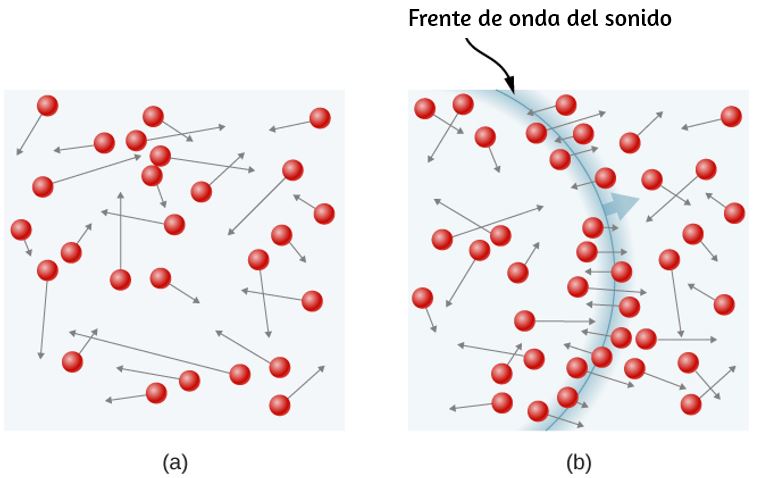
Ejemplo 2.5
Cálculo de temperatura: velocidad de escape de los átomos de helio
Para escapar de la gravedad de la Tierra, un objeto cerca de la parte superior de la atmósfera (a una altitud de $100 km$) debe alejarse de la Tierra a $11.1 km/s$. Esta velocidad se llama velocidad de escape. ¿A qué temperatura los átomos de helio tendrán una velocidad $rms$ igual a la velocidad de escape?
Estrategia
Identifica los datos conocidos y las incógnitas y determina qué ecuaciones usar para resolver el problema.
Solución
Explicación
Esta temperatura es mucho más alta que la temperatura atmosférica, que es de aproximadamente $250 K$ ($-25 °C$ o $-10 °F$) a gran altitud. Muy pocos átomos de helio quedan en la atmósfera, pero muchos estaban presentes cuando se formó la atmósfera, y cada vez más se crean por la desintegración radiactiva. La razón de la pérdida de átomos de helio es que una pequeña cantidad de átomos de helio tiene velocidades más altas que la velocidad de escape de la Tierra, incluso a temperaturas normales. La velocidad de un átomo de helio cambia de una colisión a la siguiente, de modo que en cualquier momento, hay una posibilidad pequeña pero distinta de cero de que la velocidad del átomo sea mayor que la velocidad de escape.
La posibilidad es lo suficientemente alta como para que durante la vida de la Tierra, casi todos los átomos de helio que han estado en la atmósfera hayan alcanzado la velocidad de escape a grandes altitudes y escapado de la atracción gravitacional de la Tierra. Las moléculas más pesadas, como el oxígeno, el nitrógeno y el agua, tienen velocidades rms más pequeñas, por lo que es mucho menos probable que cualquiera de ellas tenga velocidades mayores que la velocidad de escape.
De hecho, la probabilidad es tan pequeña que se requieren miles de millones de años para perder cantidades significativas de moléculas más pesadas de la atmósfera. La muestra el efecto de la falta de una atmósfera en la Luna. Debido a que la atracción gravitatoria de la Luna es mucho más débil, ha perdido casi toda su atmósfera.

 Comprueba tu aprendizaje 2.4
Comprueba tu aprendizaje 2.4
La presión que crearía un gas si ocupaba el volumen total disponible se denomina presión parcial del gas. Si se mezclan dos o más gases, llegarán al equilibrio térmico como resultado de colisiones entre moléculas; el proceso es análogo a la conducción de calor como se describe en el capítulo sobre temperatura y calor. Como hemos visto en la teoría cinética, cuando los gases tienen la misma temperatura, sus moléculas tienen la misma energía cinética promedio. Por lo tanto, cada gas obedece a la ley de los gases ideales por separado y ejerce la misma presión sobre las paredes de un contenedor que si estuviera solo. Por lo tanto, en una mezcla de gases, la presión total es la suma de las presiones parciales de los gases componentes, suponiendo un comportamiento ideal del gas y sin reacciones químicas entre los componentes. Esta ley se conoce como la ley de Dalton de presiones parciales, después del científico inglés John Dalton (1766-1844), quien la propuso. La ley de Dalton es consistente con el hecho de que las presiones se agregan de acuerdo con el principio de Pascal.
En una mezcla de gases ideales en equilibrio térmico, el número de moléculas de cada gas es proporcional a su presión parcial.
Este resultado se sigue de aplicar la ley de los gases ideales a cada uno en la forma $p/n = RT/V$. Debido a que el lado derecho es el mismo para cualquier gas a una temperatura dada en un contenedor de un volumen dado, el lado izquierdo también es el mismo.
Una aplicación importante de la presión parcial es que, en química, funciona como la concentración de un gas para determinar la velocidad de una reacción. Aquí, solo mencionamos que la presión parcial de oxígeno en los pulmones de una persona es crucial para la vida y la salud. Respirar aire que tiene una presión parcial de oxígeno por debajo de $0.16 atm$ puede afectar la coordinación y el juicio, especialmente en personas que no están aclimatadas a una elevación alta. Las presiones parciales más bajas de $O_2$ tienen efectos más serios; las presiones parciales inferiores a $0.06 atm$ pueden ser rápidamente fatales, y es probable que se produzca un daño permanente incluso si la persona es rescatada. Sin embargo, la sensación de necesitar respirar, como cuando se contiene la respiración, es causada mucho más por las altas concentraciones de dióxido de carbono en la sangre que por bajas concentraciones de oxígeno. Por lo tanto, si una habitación pequeña o clóset está llena de aire con baja concentración de oxígeno, tal vez porque se almacena allí un cilindro de algún gas comprimido, una persona no sentirá ninguna sensación de "asfixia" y puede entrar en convulsiones o perder el conocimiento sin notar nada mal. Los ingenieros de seguridad prestan considerable atención a este peligro.
Otra aplicación importante de la presión parcial es la presión de vapor, que es la presión parcial de un vapor el que está en equilibrio con la fase líquida (o sólida, en el caso de la sublimación) de la misma sustancia. A cualquier temperatura, la presión parcial del agua en el aire no puede exceder la presión de vapor del agua a esa temperatura, porque cada vez que la presión parcial alcanza la presión de vapor, el agua se condensa fuera del aire. El rocío es un ejemplo de esta condensación. La temperatura a la que se produce la condensación para una muestra de aire se denomina punto de rocío. Se mide fácilmente enfriando lentamente una bola de metal; el punto de rocío es la temperatura a la cual la condensación aparece por primera vez en la bola.
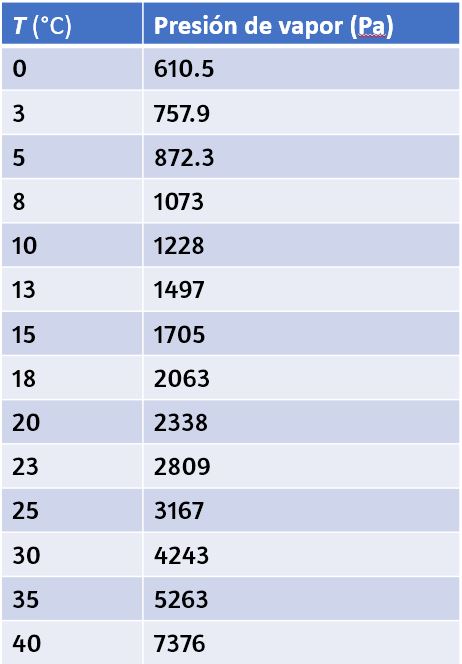
Las presiones de vapor de agua a algunas temperaturas de interés para la meteorología se dan en la
La humedad relativa ($RH$) a una temperatura $T$ se define por
$$RH = \frac{\textsf{Presión parcial del vapor de agua en }T}{\textsf{Presión del vapor de agua en }T} × 100\%$$Una humedad relativa del $100\%$ significa que la presión parcial del agua es igual a la presión de vapor; en otras palabras, el aire está saturado de agua.
Ejemplo 2.6
Cálculo de la humedad relativa
¿Cuál es la humedad relativa cuando la temperatura del aire es de $25 °C$ y el punto de rocío es de $15 °C$?
Estrategia
Simplemente buscamos la presión de vapor a la temperatura dada y la del punto de rocío y buscamos la relación.
Solución
$$\begin{align*} RH &= \frac{\textsf{Presión parcial del vapor de agua en }15 °C}{\textsf{Presión del vapor de agua en }25 °C} × 100\% \\ \\ &= \frac{1705 Pa}{3167 Pa} = 53.8\% \end{align*}$$Explicación
El $RH$ es importante para nuestra comodidad. El valor de $53.8$% se encuentra dentro del rango de $40$% a $60$% recomendado para la comodidad en interiores. Como se señaló en el capítulo sobre temperatura y calor, la temperatura rara vez cae por debajo del punto de rocío, porque cuando alcanza el punto de rocío o escarcha, el agua se condensa y libera una cantidad relativamente grande de calor latente de vaporización.
Ahora consideramos colisiones explícitamente. El primer paso habitual (que es todo lo que tomaremos) es calcular la trayectoria libre media, $λ$, la distancia promedio que una molécula viaja entre colisiones con otras moléculas, y el tiempo libre medio $τ$, el tiempo promedio entre las colisiones de un molécula. Si suponemos que todas las moléculas son esferas con un radio $r$, entonces una molécula colisionará con otra si sus centros están a una distancia de $2r$ entre sí. Para una partícula dada, decimos que el área de un círculo con ese radio, $4πr^2$, es la "sección transversal" para las colisiones. A medida que la partícula se mueve, traza un cilindro con esa área transversal. La trayectoria libre media es la longitud $λ$ de modo que el número esperado de otras moléculas en un cilindro de longitud $λ$ y una sección transversal $4πr^2$ es $1$. Si temporalmente ignoramos el movimiento de las moléculas distintas de la que estamos viendo, el número esperado es la densidad numérica de las moléculas, $N/V$, multiplicado por el volumen, y el volumen es $4πr^2λ$, por lo que tenemos $(N/V)4πr^2λ = 1$, o
$$λ = \frac{V}{4πr^2N}$$Tener en cuenta el movimiento de todas las moléculas hace que el cálculo sea mucho más difícil, pero el único cambio es un factor de $\sqrt{2}$. El resultado es
En un gas ideal, podemos sustituir $V/N = k_BT/p$ para obtener
El tiempo libre medio $τ$ es simplemente el camino libre medio dividido por la velocidad típica, y la opción habitual es la velocidad $rms$. Entonces
Ejemplo 2.7
Cálculo del tiempo libre promedio
Encuentra el tiempo libre promedio para los átomos de argón ($M = 39.9 g/mol$) a una temperatura de $0 °C$ y una presión de $1.00 atm$. Toma el radio de un átomo de argón de $1.70 × 10^{-10} m$.
Solución
1. Identifica los datos conocidos y convierte en unidades del SI. Sabemos que la masa molar es $0.0399 kg/mol$, la temperatura es $273 K$, la presión es $1.01 × 10^5 Pa$ y el radio es $1.70 × 10^{-10} m$.
2. Encuentre la velocidad $rms$: $v_{\textsf{rms}} = \sqrt{3RT/M} = 413 m/s$
3. Sustituye en la ecuación para el tiempo libre medio:
$$\begin{align*} τ &= \frac{k_BT}{4\sqrt{2}πr^2pv_{\textsf{rms}}} \\ &= \frac{(1.38 × 10^{-23} J/K)(273 K)}{4\sqrt{2}π(1.70 × 10^{-10} m)^2(1.01 × 10^5 Pa)(413 m/s)} \\ \\ τ &= 1.76 × 10^{-10} s \end{align*}$$Explicación
Difícilmente podemos comparar este resultado con nuestra intuición sobre las moléculas de gas, pero nos da una imagen de las moléculas que colisionan con una frecuencia extremadamente alta.
 Comprueba tu aprendizaje 2.5
Comprueba tu aprendizaje 2.5
En el capítulo sobre temperatura y calor, definimos la capacidad de calor específica con la ecuación $Q = mcΔT$, o $c = (1/m)Q/ΔT$. Sin embargo, las propiedades de un gas ideal dependen directamente del número de moles en una muestra, por lo que aquí definimos la capacidad de calor específica en términos del número de moles, no de la masa. Además, cuando hablamos de sólidos y líquidos, ignoramos cualquier cambio en el volumen y la presión con los cambios de temperatura, una buena aproximación para sólidos y líquidos, pero para los gases, tenemos que condicionar el volumen o los cambios de presión. Aquí, nos enfocamos en la capacidad de calor con el volumen constante. Podemos calcularlo para un gas ideal.
Definimos la capacidad de calor molar a de volumen constante $C_V,$ como
$C_V = \frac{1}{n} \frac{Q}{ΔT}$, con $V$ constante
Esto a menudo se expresa de la forma
Si el volumen no cambia, no hay desplazamiento total, por lo que no se realiza ningún trabajo, y el único cambio en la energía interna se debe al flujo de calor $ΔE_{\textsf{int}} = Q$ (esta afirmación se trata más adelante en el próximo capítulo).
Usamos la ecuación $E_{\textsf{int}} = 3nRT/2$ para escribir $ΔE_{\textsf{int}} = 3nRΔT/2$ y sustituimos $ΔE$ por $Q$ para encontrar $Q = 3nRΔT/2$, lo que da el siguiente resultado simple para un ideal gas monoatómico:
$$C_V = \frac{3}{2}R$$Es independiente de la temperatura, lo que justifica el uso de diferencias finitas en lugar de derivadas. Esta fórmula concuerda bien con los resultados experimentales.
En el próximo capítulo discutiremos el calor específico molar a presión constante $C_p$, que siempre es mayor que $C_V$.
Ejemplo 2.8
Cálculo de temperatura
Una muestra de $0.125 kg$ de xenón está contenida en un cilindro de metal rígido, lo suficientemente grande como para que el xenón se pueda modelar como un gas ideal, a una temperatura de $20.0 °C$. El cilindro se mueve afuera en un caluroso día de verano. Cuando el xenón entra en equilibrio al alcanzar la temperatura de su entorno, se le conducen $180 J$ de calor a través de las paredes del cilindro. ¿Cuál es la temperatura de equilibrio? Desprecia la expansión del cilindro de metal.
Solución
La masa molar de xenón es $131.3 g$, entonces obtenemos:
$$n = \frac{125 g}{131.3 g/mol} = 0.952 mol$$Por lo tanto, la temperatura final es de $35.2 °C$. El problema también podría resolverse en kelvin; como un kelvin es del mismo tamaño que un grado Celsius de cambio de temperatura, obtendrías $ΔT = 15.2 K$.
Explicación
El calentamiento de un gas ideal o casi ideal a volumen constante es importante en los motores de los automóviles y muchos otros sistemas prácticos.
 Comprueba tu aprendizaje 2.6
Comprueba tu aprendizaje 2.6
Nos gustaría generalizar nuestros resultados a los gases ideales con más de un átomo por molécula. En tales sistemas, las moléculas pueden tener otras formas de energía además de la energía cinética de traslación, como la energía cinética de rotación y las energías cinéticas y potenciales de vibración. Veremos que una regla simple nos permite determinar las energías promedio presentes en estas formas y resolver problemas de forma muy similar a como lo hicimos con los gases monoatómicos.
En la sección anterior, encontramos que $\frac{1}{2}m \={v}^2 = \frac{3}{2}k_BT$ y $\={v}^2 = 3\={v}_x^2$, de lo cual se deduce que $\frac{1}{2}m \={v}_x^2 = \frac{3}{2}k_BT$. La misma ecuación vale para $\frac{1}{2}m \={v}_y^2$ y para $\frac{1}{2}m \={v}_z^2$. Por lo tanto, podemos ver nuestra energía de $\frac{3}{2}k_BT$ como la suma de las contribuciones de $\frac{1}{2}k_BT$ de cada una de las tres dimensiones del movimiento traslacional. Cambiando al gas como un todo, vemos que el 3 en la fórmula $C_V = \frac{3}{2}R$ también refleja esas tres dimensiones. Definimos un grado de libertad como un movimiento posible independiente de la molécula, como cada una de las tres dimensiones de la traslación. Entonces, dejando que d represente el número de grados de libertad, la capacidad de calor molar a volumen constante de un gas ideal monoatómico es $C_V = \frac{d}{2}R$, donde $d = 3$.
Teorema de equipartición
La energía de un sistema termodinámico en equilibrio se divide por igual entre sus grados de libertad. En consecuencia, la capacidad de calor molar de un gas ideal es proporcional a su número de grados de libertad, $d$:
$$C_V = \frac{d}{2}R \tag{2.14}$$Este resultado se debe al físico escocés James Clerk Maxwell (1831-1871), cuyo nombre aparecerá varias veces más en este libro.
Por ejemplo, considera un gas ideal diatómico (un buen modelo para nitrógeno, $N_2$ y oxígeno, $O_2$). Tal gas tiene más grados de libertad que un gas monoatómico. Además de los tres grados de libertad para la traducción, tiene dos grados de libertad para la rotación perpendicular a su eje. Además, la molécula puede vibrar a lo largo de su eje. Este movimiento a menudo se modela imaginando un resorte que conecta los dos átomos, y sabemos por el movimiento armónico simple que dicho movimiento tiene tanto energía cinética como potencial. Cada una de estas formas de energía corresponde a un grado de libertad, dando dos más.
Podríamos esperar que para un gas diatómico, deberíamos usar 7 como el número de grados de libertad; Clásicamente, si las moléculas de un gas solo tuvieran energía cinética de traslación, las colisiones entre las moléculas pronto las harían rotar y vibrar. Sin embargo, como se explicó en el módulo anterior, la mecánica cuántica controla qué grados de libertad están activos. El resultado se muestra en la . Ambas energías rotacionales y vibratorias están limitadas a valores discretos. Para temperaturas inferiores a $60 K$, las energías de las moléculas de hidrógeno son demasiado bajas para que una colisión lleve el estado de rotación o estado vibratorio de una molécula desde la energía más baja al segundo más bajo, por lo que la única forma de energía es la energía cinética de traslación. $d = 3$ o $C_V = 3R/2$ como en un gas monoatómico. Por encima de esa temperatura, los dos grados de libertad de rotación comienzan a contribuir, es decir, algunas moléculas se excitan al estado de rotación con la segunda energía más baja (Esta temperatura es mucho más baja que la que aportan las rotaciones de gases monoatómicos, porque las moléculas diatómicas tienen inercias rotacionales mucho más altas y, por lo tanto, energías rotacionales mucho más bajas).
Desde aproximadamente temperatura ambiente (un poco menos de $300 K$) hasta $600 K$, la rotación en los grados de libertad están completamente activos, pero los vibratorios no, y $d = 5$. Luego, finalmente, por encima de aproximadamente $3000 K$, los grados de libertad vibratorios están completamente activos, y $d = 7$ como predijo la teoría clásica.
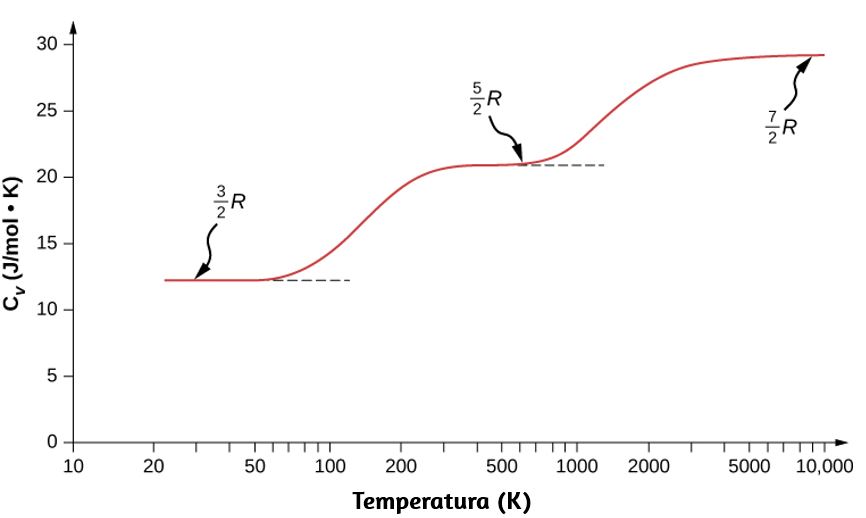
Las moléculas poliatómicas tienen típicamente un grado de libertad rotacional adicional a temperatura ambiente, ya que tienen momentos de inercia comparables alrededor de cualquier eje.
Por lo tanto, a temperatura ambiente, tienen $d = 6$, y a alta temperatura, $d = 8$. Generalmente suponemos que los gases tienen los valores teóricos de temperatura ambiente de $d$.
Como se muestra en la , los resultados concuerdan bien con los experimentos para muchos gases monoatómicos y diatómicos, pero el acuerdo para los gases triatómicos es justo. Las diferencias surgen de las interacciones que hemos ignorado entre y dentro de las moléculas.
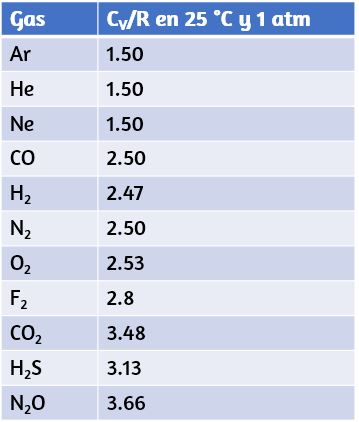
¿Qué pasa con la energía interna para gases diatómicos y poliatómicos? Para tales gases, $C_V$ es una función de la temperatura (), por lo que no tenemos el tipo de resultado simple que tenemos para los gases ideales monoatómicos.
La idea de la equipartición conduce a una estimación de la capacidad de calor molar de los elementos sólidos a temperaturas ordinarias. Podemos modelar los átomos de un sólido como unidos a los átomos vecinos por resortes ().
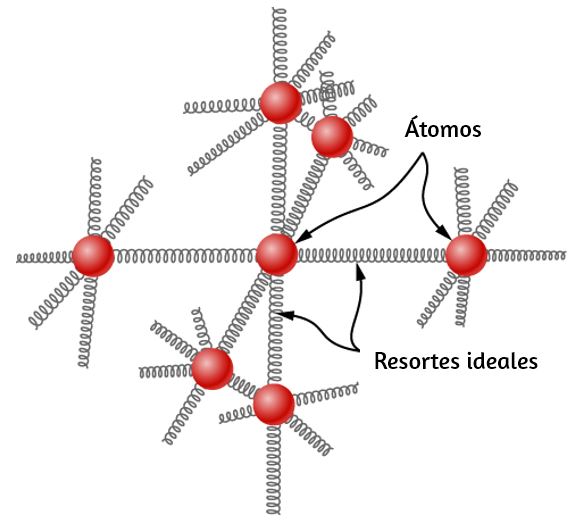
Análogamente a la discusión de la vibración en el módulo anterior, cada átomo tiene seis grados de libertad: una cinética y uno potencial para cada una de las direcciones $x$, $y$, y $z$. En consecuencia, el calor específico molar de un metal debe ser $3R$.
Este resultado, conocido como la Ley de Dulong y Petit, funciona bastante bien experimentalmente a temperatura ambiente (Por cada elemento, falla a bajas temperaturas por razones mecánico-cuánticas. Como los efectos cuánticos son particularmente importantes para partículas de baja masa, la Ley de Dulong y Petit ya falla a temperatura ambiente para algunos elementos ligeros, como el berilio y el carbono. También falla para algunos elementos más pesados por varias razones más allá de lo que podemos cubrir).
Estrategia de resolución de problemas: capacidad de calor y equipartición
La estrategia para resolver estos problemas es la misma que en Cambios de fase para los efectos de la transferencia de calor. La única característica nueva es que debes determinar si el caso que acabamos de presentar (gases ideales a volumen constante) se aplica al problema (Para los elementos sólidos, buscar la capacidad calorífica específica generalmente es mejor que estimarla a partir de la Ley de Dulong y Petit). En el caso de un gas ideal, determina el número d de grados de libertad a partir del número de átomos en la molécula del gas y úsala para calcular $C_V$.Ejemplo 2.9
Cálculo de temperatura: Calorimetría con un gas ideal
Una pieza de $300 g$ de galio sólido (un metal usado en dispositivos semiconductores) en su punto de fusión de solo $30.0 °C$ está en contacto con $12.0$ moles de aire (supuestamente diatómico) a $95.0 °C$ en un recipiente aislado. Cuando el aire alcanza el equilibrio con el galio, se han derretido $202 g$ del galio.
Con base a esos datos, ¿cuál es el calor de fusión del galio? Supón que el volumen del aire no cambia y que no hay otras transferencias de calor.
Estrategia
Usaremos la ecuación $Q_{\textsf{caliente}} + Q_{\textsf{frío}} = 0$. Como parte del galio no se derrite, sabemos que la temperatura final sigue siendo el punto de fusión. Entonces, el único $Q_{\textsf{caliente}}$ es el calor perdido a medida que el aire se enfría, $Q_{\textsf{caliente}} = n_{\textsf{aire}}C_VΔT$, donde $C_V = 5R/2$. El único $Q_{\textsf{frío}}$ es el calor latente de fusión del galio, $Q_{\textsf{frío}} = m_{Ga}L_f$. Es positivo porque el calor fluye al galio.
Solución
1. Configura la ecuación:
$$n_{\textsf{aire}}C_VΔT + m_{Ga}L_f = 0$$Sustituye los valores conocidos y halla:
Resolvemos para encontrar que el calor de fusión del galio es $80.2 kJ/kg$.
En el siguiente objeto interactivo, diseñado en la Universidad de Texas, podrás interactuar con un simulador de gas. Puedes controlar las cantidades relativas de dos gases, $A$ y $B$ con el mango de la bomba. Puedes liberar gas con la válvula de liberación. La temperatura la puedes subir y bajar, además puedes tener volumen bloqueado o cambiar. Juega con él y observa las relaciones de $P$, $V$, $n$ y $T$.
Las partículas en un gas ideal viajan a velocidades relativamente altas, pero no viajan a la misma velocidad. La velocidad rms es un tipo de promedio, pero muchas partículas se mueven más rápido y muchas se mueven más despacio. La distribución real de velocidades tiene varias implicaciones interesantes para otras áreas de la física, como veremos en capítulos posteriores.
El movimiento de las moléculas en un gas es aleatorio en magnitud y dirección para moléculas individuales, pero un gas de muchas moléculas tiene una distribución predecible de velocidades moleculares.
Esta distribución predecible de velocidades moleculares se conoce como la distribución de Maxwell-Boltzmann, después de sus originadores, quienes la calcularon basándose en la teoría cinética, y desde entonces se ha confirmado experimentalmente ().
Para entender esta figura, debemos definir una función de distribución de velocidades moleculares, ya que con un número finito de moléculas, la probabilidad de que una molécula tenga exactamente una velocidad dada es $0$. Definimos la función de distribución $f(v)$ diciendo que el número esperado $N(v_1, v_2)$ de partículas con velocidades entre $v_1$ y $v_2$ está dado por
$$N(v_1, v_2) = N \int_{v_1}^{v_2} f(v)dv$$Dado que $N$ es adimensional, la unidad de $f(v)$ es segundos por metro. Podemos escribir esta ecuación convenientemente en forma diferencial:
$$dN = Nf(v)dv$$De esta forma, podemos entender la ecuación diciendo que el número de moléculas con velocidades entre $v$ y $v + dv$ es el número total de moléculas en los tiempos de la muestra $f(v)$ veces $dv$. Es decir, la probabilidad de que la velocidad de una molécula esté entre $v$ y $v + dv$ es $f(v)dv$.
Ahora podemos citar el resultado de Maxwell, aunque la prueba está más allá de nuestro alcance.
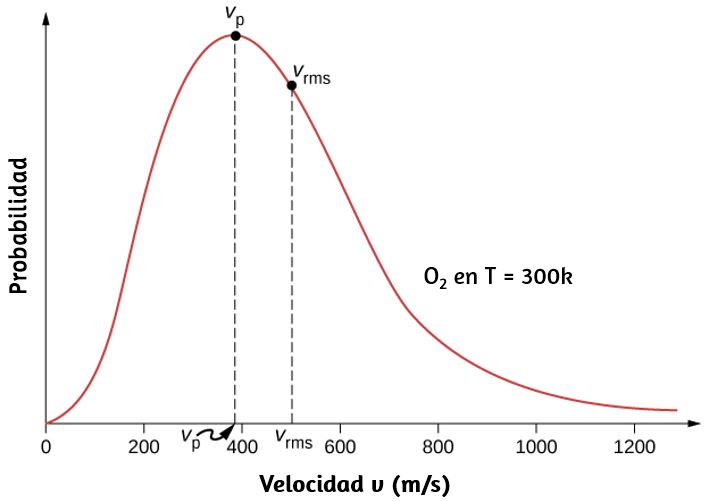
Maxwell-Boltzmann distribución de velocidades
La función de distribución para velocidades de partículas en un gas ideal a temperatura $T$ es
$$f(v) = \frac{4}{\sqrt{π}} \left(\frac{m}{2k_BT} \right)^{3/2}v^2e^{−mv^2/2k_BT} \tag{2.15}$$Los factores antes de $v^2$ son constantes de normalización; se aseguran de que $N(0, ∞) = N$ asegurándose que
$$\int_0^∞ f(v)dv = 1$$Centrémonos en la dependencia de $v$. El factor de $v^2$ significa que $f(0) = 0$ y para $v$ pequeña, la curva se parece a una parábola. El factor de $e^{-m_0v^2/2k_BT}$ significa que
$$\lim{v → ∞} f(v) = 0$$y el gráfico tiene una cola exponencial, lo que indica que algunas moléculas pueden moverse varias veces a la velocidad rms. La interacción de estos factores da la forma de una función de un solo pico que se muestra en la figura.
Ejemplo 2.10
Cálculo de la relación de números de moléculas a velocidades cercanas
En una muestra de nitrógeno ($N_2$, con una masa molar de $28.0 g/mol)$ a una temperatura de $273 °C$, encuentra la relación del número de moléculas con una velocidad muy cercana a $300 m/s$, con la velocidad muy cercana de $100 m/s$.
Estrategia
Dado que estamos viendo un rango pequeño, podemos aproximar el número de moléculas cercanas a $100 m/s$ como $dN_{100} = f(100 m/s)dv$. Entonces, la relación que queremos es
Todo lo que tenemos que hacer es tomar la relación de los dos valores $f$.
Solución
1. Identifique los datos dados y conviértelos a unidades del SI si es necesario.
$T = 300 K$, $k_B = 1.38 × 10^{-23} J/K$
$M = 0.0280 kg/mol$, por lo tanto $m = 4.65 × 10^{-26} kg$
2. Sustituye los valores y resuelve.
La muestra que la curva se desplaza a velocidades más altas a temperaturas más altas, con un rango más amplio de velocidades.
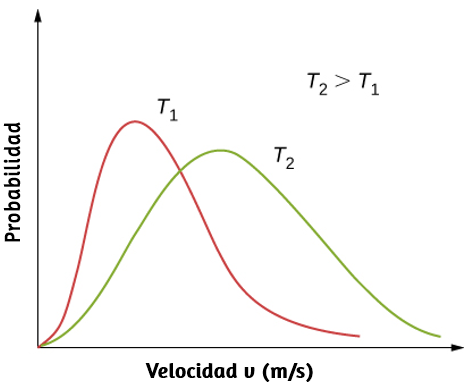
Podemos usar una distribución de probabilidad para calcular los valores promedio al multiplicar la función de distribución por la cantidad a promediar, e integrar el producto en todas las velocidades posibles (Esto es análogo al cálculo de promedios de distribuciones discretas, donde se multiplica cada valor por el número de veces que ocurre, se suman los resultados y se dividen por el número de valores. La integral es análoga a los primeros dos pasos, y la normalización es análoga a la división por el número de valores). Por lo tanto, la velocidad promedio es
Similarmente,
$$v_p = \sqrt{\={v}^2} = \sqrt{\int_0^∞ v^2 f(v)dv} = \sqrt{\frac{3k_BT}{m}} = \sqrt{3RT}{M}$$La velocidad más probable, también llamada la velocidad máxima $v_p$, es la velocidad en el pico de la distribución de la velocidad (En las estadísticas se llamaría el modo). Es menor que la velocidad rms. La velocidad más probable se puede calcular mediante el método más familiar de establecer la derivada de la función de distribución, con respecto a $v$, igual a $0$. El resultado es
que es menos que $v_{rms}$. De hecho, la velocidad rms es mayor que la velocidad más probable y la velocidad promedio.
La velocidad máxima proporciona una forma a veces más conveniente para escribir la función de distribución de Maxwell-Boltzmann:
$$f(v) = \frac{4v^2}{\sqrt{π} v_p^3} e^{-v^2/v_p^2}$$En el factor $e^{-mv^2/2k_BT}$, es fácil reconocer la energía cinética de la traslación. Por lo tanto, esa expresión es igual a $e^{-K/k_BT}$. La distribución $f(v)$ se puede transformar en una distribución de energía cinética al requerir que $f(K)dK = f(v)dv$. Boltzmann demostró que la fórmula resultante es mucho más aplicable en general si reemplazamos la energía cinética de la traslación con la energía mecánica total. El resultado de E. Boltzmann es
$$f(E) = \frac{2}{\sqrt{π}} (k_BT)^{-3/2} \sqrt{E} e^{-E/k_BT} = \frac{2}{\sqrt{π}(k_BT)^{3/2}} \frac{\sqrt{R}}{e^{E/k_BT}}$$La primera parte de esta ecuación, con la exponencial negativa, es la forma habitual de escribirla. Damos la segunda parte solo para observar que $e^{E/k_BT}$ en el denominador es omnipresente tanto en la mecánica estadística cuántica como en la clásica.
Estrategia de resolución de problemas: distribución de velocidad
Paso 1. Examina la situación para determinar que se relaciona con la distribución de velocidades moleculares.
Paso 2. Haz una lista de las cantidades que se dan o se pueden inferir del problema tal como se establece (identifica las cantidades conocidas).
Paso 3. Identifica exactamente qué debe determinarse en el problema (identifica las incógnitas). Una lista escrita es útil.
Paso 4. Convierte los valores conocidos en unidades del SI adecuadas ($K$ para temperatura, $Pa$ para presión, $m^3$ para volumen, moléculas para $N$ y moles para $n$). Sin embargo, en muchos casos, usar $R$ y la masa molar será más conveniente que usar $k_B$ y la masa molecular.
Paso 5 Determina si necesitas la función de distribución para la velocidad o la de la energía, y si estás utilizando una fórmula para una de las velocidades características (promedio, muy probablemente, o $rms$), encontrando una relación de valores de la función de distribución , o aproximando una integral.
Paso 6. Resuelve la ecuación apropiada para la ley de los gases ideales para la cantidad que se determinará (la incognita). Ten en cuenta que si estás tomando una proporción de valores de la función de distribución, los factores de normalización se dividen. O si se aproxima a una integral, usa el método solicitado en el problema.
Paso 7. Sustituye las cantidades conocidas, junto con sus unidades, en la ecuación apropiada y obtén soluciones numéricas completas con unidades.
Ahora podemos obtener una comprensión cualitativa de un rompecabezas sobre la composición de la atmósfera de la Tierra. El hidrógeno es, con mucho, el elemento más común en el universo, y el helio es por lejos el segundo más común. Además, el helio se produce constantemente en la Tierra por la desintegración radiactiva.
¿Por qué esos elementos son tan raros en nuestra atmósfera? La respuesta es que las moléculas de gas que alcanzan velocidades superiores a la velocidad de escape de la Tierra, de aproximadamente 11 km/s, pueden escapar de la atmósfera hacia el espacio. Debido a la menor masa de moléculas de hidrógeno y helio, se mueven a velocidades más altas que otras moléculas de gas, como el nitrógeno y el oxígeno. Solo unos pocos superan la velocidad de escape, pero muchas menos moléculas pesadas lo hacen. Por lo tanto, durante los miles de millones de años que la Tierra ha existido, muchas más moléculas de hidrógeno y helio han escapado de la atmósfera que otras moléculas, y casi ninguna de las dos está presente.
También podemos echar un vistazo al enfriamiento por evaporación, que discutimos en el capítulo sobre temperatura y calor. Los líquidos, como los gases, tienen una distribución de energías moleculares. Las moléculas de mayor energía son aquellas que pueden escapar de las atracciones intermoleculares del líquido. Por lo tanto, cuando se evapora algo de líquido, las moléculas que se quedan tienen una energía promedio menor y el líquido tiene una temperatura más baja.
Para terminar este capítulo, te dejamos una interesante tabla periódica, diseñada por Keith Enevoldsen (Seattle, USA).
Además del nombre, el símbolo y el número atómico del elemento, cada cuadro de elemento contiene una descripción textual de las propiedades físicas del elemento y una lista de varios de sus usos humanos y/o ocurrencias naturales. La tabla tiene un código de colores para mostrar los grupos químicos, y cada grupo se describe en un panel del mismo color. Otros paneles de información describen la estructura atómica, los enlaces químicos y la radioactividad.
Recuerda que en la barra de herramientas puedes abrir otra tabla periódica, diseñada por Juan Guillermo Rivera Berrío. Haz clic sobre algún elemento y lee la información dada

Los gases están literalmente a nuestro alrededor: el aire que respiramos es una mezcla de gases. Otros gases incluyen los que hacen que los panes y las tortas sean blandos, los que hacen que las bebidas sean gaseosas, y los que se queman para calentar muchas casas. Los motores y los refrigeradores dependen del comportamiento de los gases, como veremos en capítulos posteriores.
El calor es la transferencia de energía debido a una diferencia de temperatura entre dos sistemas. El calor describe el proceso de conversión de una forma de energía a otra. El motor de un automóvil, por ejemplo, quema gasolina. El calor se produce cuando el combustible quemado se transforma químicamente en principalmente $CO_2$ y $H_2O$, que son gases a la temperatura de combustión.
Estos gases ejercen una fuerza sobre un pistón a través de un desplazamiento, trabajando y convirtiendo la energía cinética del pistón en una variedad de otras formas, en la energía cinética del automóvil; en energía eléctrica para hacer funcionar las bujías, la radio y las luces; y de vuelta a la energía almacenada en la batería del automóvil.
La energía se conserva en todos los procesos, incluidos los asociados con los sistemas termodinámicos. Los roles de la transferencia de calor y el cambio de energía interno varían de un proceso a otro y afectan la forma en que el sistema realiza el trabajo en ese proceso. Veremos que la primera ley de la termodinámica explica que un cambio en la energía interna de un sistema proviene de cambios en el calor o el trabajo. Comprender las leyes que rigen los procesos termodinámicos y la relación entre el sistema y su entorno es, por lo tanto, primordial para obtener conocimiento científico sobre el consumo de energía y la energía misma.
Un sistema termodinámico incluye cualquier cosa cuyas propiedades termodinámicas sean de interés. Está incrustado en su entorno o ambiente; puede intercambiar calor con su entorno y trabajar en él a través de un límite o frontera, que es la pared imaginada que separa el sistema y el entorno (). En realidad, el entorno inmediato del sistema está interactuando directamente con él y, por lo tanto, tiene una influencia mucho más fuerte en su comportamiento y propiedades. Por ejemplo, si estamos estudiando el motor de un automóvil, la gasolina ardiente dentro del cilindro del motor es el sistema termodinámico; el pistón, el sistema de escape, el radiador y el aire exterior forman el entorno del sistema.
La frontera, entonces, consiste en las superficies internas del cilindro y el pistón.
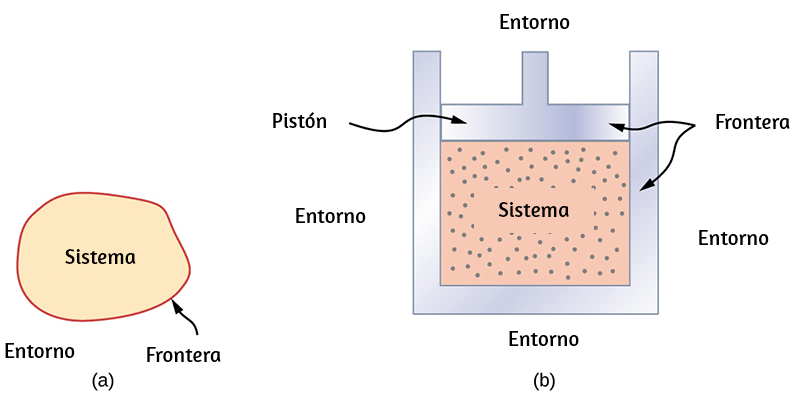
Normalmente, un sistema debe tener algunas interacciones con su entorno. Un sistema se denomina sistema aislado o cerrado si está completamente separado de su entorno, por ejemplo, un gas que está rodeado por paredes inamovibles y térmicamente aislantes. En realidad, un sistema cerrado no existe a menos que el universo entero se trate como el sistema, o se use como un modelo para un sistema real que tenga interacciones mínimas con su entorno.
La mayoría de los sistemas se conocen como sistemas abiertos, que pueden intercambiar energía y/o materia con su entorno ().
Cuando examinamos un sistema termodinámico, ignoramos la diferencia de comportamiento de un lugar a otro dentro del sistema por un momento dado. En otras palabras, nos concentramos en las propiedades macroscópicas del sistema, que son los promedios de las propiedades microscópicas de todas las moléculas o entidades en el sistema. Por lo tanto, cualquier sistema termodinámico se trata como un continuo que tiene el mismo comportamiento en todas partes. Suponemos que el sistema está en equilibrio.

Podrías tener, por ejemplo, un gradiente de temperatura en todo el sistema. Sin embargo, cuando discutimos un sistema termodinámico en este capítulo, estudiamos aquellos que tienen propiedades uniformes en todo el sistema.
Antes de que podamos llevar a cabo cualquier estudio sobre un sistema termodinámico, necesitamos una caracterización fundamental del sistema. Cuando estudiamos un sistema mecánico, nos enfocamos en las fuerzas y pares en el sistema, y el equilibrio mecánico del sistema. De manera similar, deberíamos examinar la transferencia de calor entre un sistema termodinámico y su entorno o entre las diferentes partes del sistema, y su equilibrio térmico. Intuitivamente, dicho equilibrio se alcanza si la temperatura se vuelve igual para diferentes objetos o partes del sistema en contacto térmico, y la transferencia neta de calor a lo largo del tiempo se vuelve cero.
Por lo tanto, cuando decimos que dos objetos (un sistema termodinámico y su entorno, por ejemplo) están en equilibrio térmico, queremos decir que están a la misma temperatura. Consideremos tres objetos a temperaturas $T_1$, $T_2$ y $T_3$, respectivamente. ¿Cómo sabemos si están en equilibrio térmico? El principio rector aquí es la ley zeroth (Ley Cero-ésima) de la termodinámica:
Si el objeto 1 está en equilibrio térmico con los objetos 2 y 3, respectivamente, entonces los objetos 2 y 3 también deben estar en equilibrio térmico.
Matemáticamente, podemos simplemente escribir la ley zeroth de la termodinámica
$$\textsf{Si } T_1 = T_2 \textsf{ y } T_1 = T_3, \textsf{ entonces } T_2 = T_3 \tag{3.1}$$Esta es la forma más fundamental de definir la temperatura: dos objetos deben estar a la misma temperatura termodinámicamente si la transferencia neta de calor entre ellos es cero cuando se ponen en contacto térmico y alcanzan un equilibrio térmico.
La ley zeroth de la termodinámica es igualmente aplicable a las diferentes partes de un sistema cerrado y requiere que la temperatura en todas partes dentro del sistema sea la misma si el sistema ha alcanzado un equilibrio térmico. Para simplificar nuestra discusión, suponemos que el sistema es uniforme con solo un tipo de material, por ejemplo, agua en un tanque. Las propiedades mensurables del sistema incluyen al menos su volumen, presión y temperatura. El rango de variables relevantes específicas depende del sistema. Por ejemplo, para una banda elástica estirada, las variables relevantes serían longitud, tensión y temperatura. La relación entre estas tres propiedades básicas del sistema se llama ecuación de estado del sistema y se escribe simbólicamente para un sistema cerrado como
donde $V$, $p$ y $T$ son el volumen, la presión y la temperatura del sistema en una condición dada.
En principio, esta ecuación de estado existe para cualquier sistema termodinámico, pero no siempre está disponible. Las formas de $f(p, V, T) = 0$ para muchos materiales se han determinado experimental o teóricamente. En el capítulo anterior, vimos un ejemplo de una ecuación de estado para un gas ideal, $f(p, V, T) = pV - nRT = 0$.
Hasta ahora hemos introducido varias propiedades físicas que son relevantes para la termodinámica de un sistema termodinámico, como su volumen, presión y temperatura.
Podemos separar estas cantidades en dos categorías genéricas. La cantidad asociada con una cantidad de materia es una variable extensa, como el volumen y el número de moles. Las otras propiedades de un sistema son variables intensivas, como la presión y la temperatura. Una variable extensa dobla su valor si la cantidad de materia en el sistema se duplica, siempre que todas las variables intensivas permanezcan iguales. Por ejemplo, el volumen o la energía total del sistema se duplica si duplicamos la cantidad de materia en el sistema mientras mantenemos sin cambios la temperatura y la presión del sistema.
Discutimos los conceptos de trabajo y energía anteriormente en mecánica. Los ejemplos y problemas relacionados de transferencia de calor entre diferentes objetos también se han discutido en los capítulos anteriores.
Aquí, queremos expandir estos conceptos a un sistema termodinámico y su entorno, queremos entender cómo se hace el trabajo por o para un sistema termodinámico; cómo se transfiere el calor entre un sistema y su entorno; y cómo la energía total del sistema cambia bajo la influencia del trabajo realizado y la transferencia de calor.
Una fuerza creada desde cualquier fuente puede hacer el trabajo moviendo un objeto a través de un desplazamiento. Entonces, ¿cómo funciona un sistema termodinámico? La muestra un gas confinado a un cilindro que tiene un pistón móvil en un extremo. Si el gas se expande contra el pistón, ejerce una fuerza a lo largo de una distancia y funciona sobre el pistón. Si el pistón comprime el gas cuando se mueve hacia adentro, también se trabaja, en este caso, en el gas.
El trabajo asociado con tales cambios de volumen puede determinarse de la siguiente manera: Sea o la presión del gas en la cara del pistón. Entonces la fuerza en el pistón debido al gas es $pA$, donde $A$ es el área de la cara. Cuando el pistón se empuja hacia afuera una distancia infinitesimal $dx$, la magnitud del trabajo realizado por el gas es
$$dW = Fdx = pAdx$$Como el cambio en el volumen del gas es $dV = Adx$, esto se convierte en
$$dW = pdV \tag{3.3}$$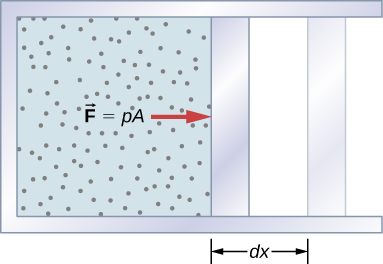
Para un cambio finito en el volumen de $V_1$ a $V_2$, podemos integrar esta ecuación entre $V_1$ y $V_2$ para encontrar el trabajo en red:
Esta integral solo es significativa para un proceso cuasiestático, lo que significa un proceso que tiene lugar en pasos infinitesimalmente pequeños, manteniendo el sistema en equilibrio térmico (Examinaremos esta idea con más detalle más adelante en este capítulo). Solo entonces existe una relación matemática bien definida (la ecuación de estado) entre la presión y el volumen. Esta relación se puede trazar en un diagrama $pV$ de presión versus volumen, donde la curva es el cambio de estado. Podemos aproximar tal proceso como uno que ocurre lentamente, a través de una serie de estados de equilibrio.
La integral se interpreta gráficamente como el área bajo la curva $pV$ (el área sombreada de la ). El trabajo realizado por el gas es positivo para la expansión y negativo para la compresión.
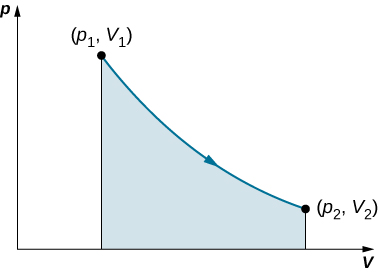
Considera los dos procesos que involucran un gas ideal que están representados por las trayectorias $AC$ y $ABC$ en la . El primer proceso es una expansión isotérmica, con el volumen del gas cambiando su volumen de $V_1$ a $V_2$. Este proceso isotérmico está representado por la curva entre los puntos $A$ y $C$. El gas se mantiene a una temperatura constante $T$ manteniéndolo en equilibrio térmico con un depósito de calor a esa temperatura. De la ecuación 3.4 y la ley de los gases ideales,
$$W = \int_{V_1}^{V_2} pdV = W = \int_{V_1}^{V_2} \frac{nRT}{V}dV$$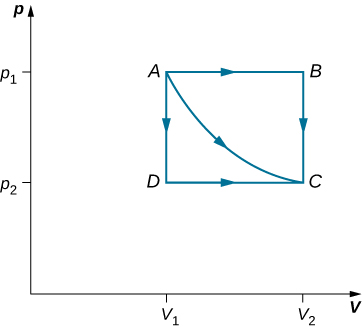
La expansión es isotérmica, por lo que $T$ permanece constante durante todo el proceso. Como $n$ y $R$ también son constantes, la única variable en el integrando es $V$, por lo que el trabajo realizado por un gas ideal en un proceso isotérmico es
$$W = nRT \int_{V_1}^{V_2} \frac{dV}{V} = nRTln \frac{V_2}{V_1}$$Observa que si $V_2 >V_1$ (expansión), $W$ es positivo, como se esperaba.
Las líneas rectas de $A$ a $B$ y luego de $B$ a $C$ representan un proceso diferente. Aquí, un gas a una presión $p_1$ primero se expande isobáricamente (presión constante) y cuasi-estáticamente desde $V_1$ a $V_2$, después de lo cual se enfría cuasi-estáticamente en el volumen constante $V_2$ hasta que su presión cae a $p_2$. De $A$ a $B$, la presión es constante en $p$, por lo que el trabajo en esta parte de la trayectoria es
De $B$ a $C$, no hay cambio en el volumen y, por lo tanto, no se realiza ningún trabajo. El trabajo neto sobre el camino $ABC$ es entonces
$$W = p_1(V_2 - V_1) + 0 = p_1(V_2 - V_1)$$Una comparación de las expresiones del trabajo realizado por el gas en los dos procesos de la muestra que son bastante diferentes. Esto ilustra una propiedad muy importante del trabajo termodinámico: depende de la ruta o trayectoria. No podemos determinar el trabajo realizado por un sistema, ya que va de un estado de equilibrio a otro a menos que sepamos su camino termodinámico. Diferentes valores del trabajo están asociados con diferentes caminos.
Ejemplo 3.1
Expansión isotérmica de un gas van der Waals
Los estudios de un gas van der Waals requieren un ajuste a la ley de los gases ideales que tenga en cuenta que las moléculas de gas tienen un volumen definido. Una mole de un gas van der Waals tiene una ecuación de estado
$$\left(p + \frac{a}{V^2} \right)(V - b) = RT$$donde $a$ y $b$ son dos parámetros para un gas específico. Supongamos que el gas se expande isotérmicamente y cuasi-estáticamente del volumen $V_1$ al volumen $V_2$. ¿Cuánto trabajo realiza el gas durante la expansión?
Estrategia
Como se da la ecuación de estado, podemos usar la Ecuación 3.4 para expresar la presión en términos de $V$ y $T$. Además, la temperatura $T$ es una constante bajo la condición isotérmica, por lo que $V$ se convierte en la única variable que cambia bajo la integral.
Solución
Para evaluar esta integral, debemos expresar $p$ en función de $V$. A partir de la ecuación de estado dada, la presión del gas es
$$p = \frac{RT}{V - b} - \frac{a}{V^2}$$Debido a que $T$ es constante bajo la condición isotérmica, el trabajo realizado por $1 mol$ de un gas de van der Waals al expandirse de un volumen $V_1$ a un volumen $V_2$ es por lo tanto
$$W = \int_{V_1}^{V_2} \frac{RT}{V - b} - \frac{a}{V^2} = RTln(V − b) + a/V|$$evaluada entre $V_1$ y $V_2$
$$= RT \, ln \left(\frac{V_2 - b}{V_1 - b} \right) + a \left(\frac{1}{V_2} - \frac{1}{V_1} \right)$$Explicación
Al tomar en cuenta el volumen de las moléculas, la expresión para el trabajo es mucho más compleja. Sin embargo, si establecemos $a = 0$ y $b = 0$, vemos que la expresión de trabajo coincide exactamente con el trabajo realizado por un proceso isotérmico para una mol de un gas ideal.
 Comprueba tu aprendizaje 3.1
Comprueba tu aprendizaje 3.1
La energía interna $E_{\textsf{int}}$ de un sistema termodinámico es, por definición, la suma de las energías mecánicas de todas las moléculas o entidades en el sistema. Si las energías cinéticas y potenciales de la molécula $i$ son $K_i$ y $U_i$, respectivamente, entonces la energía interna del sistema es el promedio de la energía mecánica total de todas las entidades:
donde la sumatoria está sobre todas las moléculas del sistema, y las barras sobre $K$ y $U$ indican valores promedio. La energía cinética $K_i$ de una molécula individual incluye contribuciones debidas a su rotación y vibración, así como su energía traslacional $m_iv_i^2/2$, donde $v_i$ es la velocidad de la molécula medida con relación al centro de masa del sistema. La energía potencial $U_i$ está asociada solo con las interacciones entre la molécula $i$ y las otras moléculas del sistema. De hecho, ni la ubicación del sistema ni su movimiento tienen ninguna consecuencia en lo que respecta a la energía interna. La energía interna del sistema no se ve afectada moviéndolo del sótano al techo de un edificio de 100 pisos o colocándolo en un tren en movimiento.
En un gas monoatómico ideal, cada molécula es un solo átomo. En consecuencia, no hay energía cinética de rotación o vibración y $K_i = m_iv_i^2/2$. Además, no hay interacciones interatómicas (a pesar de las colisiones), así que $U_i = constante$, que establecemos en cero. Por lo tanto, la energía interna se debe a la energía cinética de la traslación únicamente y
$$E_{\textsf{int}} = \sum_i \={K}_i = \sum_i \frac{1}{2}m_i \={v}_i^2$$De la discusión en el capítulo anterior, sabemos que la energía cinética promedio de una molécula en un gas monoatómico ideal es
$$\frac{1}{2}m_i \={v}_i^2 = \frac{3}{2}k_BT$$donde $T$ es la temperatura en grados Kelvin del gas. En consecuencia, la energía mecánica promedio por molécula de un gas monoatómico ideal es también de $3k_BT/2$, es decir,
$$\={K_i + U_i} \, \={K}_i = \frac{3}{2}k_BT$$La energía interna es solo el número de moléculas multiplicado por la energía mecánica promedio por molécula. Por lo tanto, para $n$ moles de un gas monoatómico ideal,
Ten en cuenta que la energía interna de una cantidad dada de un gas monoatómico ideal depende de la temperatura y es completamente independiente de la presión y el volumen del gas. Para otros sistemas, la energía interna no se puede expresar de manera tan simple.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera B., para simplificar los cálculos, usamos $1.203 x 10 ^{-3}$ moles de gas ideal, de tal forma que la constante $nR = 10 kPacm^3K^{-1}$. Entonces, si la presión está en $kPa$ y el volumen en $cm^3$, entonces la temperatura del gas en Kelvin está dada por $T = PV/10$. Para un volumen constante, el calor agregado simplemente aumenta la energía interna del gas, la fórmula para el cambio en la energía interna ($3/2nRΔT$) se simplifica a $0.015ΔT$.
Sin embargo, un aumento en la energía interna a menudo puede asociarse con un aumento de la temperatura.
Sabemos por la ley zeroth de la termodinámica que cuando dos sistemas se colocan en contacto térmico, eventualmente alcanzan el equilibrio térmico, en cuyo punto se encuentran a la misma temperatura. Como ejemplo, supongamos que mezclamos dos gases monoatómicos ideales. Ahora, la energía por molécula de un gas monoatómico ideal es proporcional a su temperatura. Por lo tanto, cuando los dos gases se mezclan, las moléculas del gas más caliente deben perder energía y las moléculas del gas más frío deben ganar energía. Esto continúa hasta que se alcanza el equilibrio térmico, en cuyo punto, la temperatura y, por lo tanto, la energía cinética de traslación promedio por molécula, es la misma para ambos gases. El enfoque del equilibrio para los sistemas reales es algo más complicado que para un gas monoatómico ideal. Sin embargo, aún podemos decir que la energía se intercambia entre los sistemas hasta que sus temperaturas sean las mismas.
Ahora que hemos visto cómo calcular la energía interna, el calor y el trabajo realizado para un sistema termodinámico que experimenta cambios durante algún proceso, podemos ver cómo estas cantidades interactúan para afectar la cantidad de cambio que puede ocurrir. Esta interacción está dada por la primera ley de la termodinámica. Al científico y novelista británico C. P. Snow (1905-1980) se le atribuye una broma sobre las cuatro leyes de la termodinámica. Su declaración humorística de la primera ley de la termodinámica se afirma "no se puede ganar", o en otras palabras, no se puede obtener más energía de un sistema de lo que se pone en ella. Veremos en este capítulo cómo la energía interna, el calor y el trabajo juegan un papel en la primera ley de la termodinámica.
Supongamos que $Q$ representa el calor intercambiado entre un sistema y el entorno, y $W$ es el trabajo realizado por o sobre el sistema. La primera ley establece que el cambio en la energía interna de ese sistema está dado por $Q - W$. Como el calor agregado aumenta la energía interna de un sistema, $Q$ es positivo cuando se agrega al sistema y negativo cuando se elimina del sistema.
Cuando un gas se expande, funciona y su energía interna disminuye. Por lo tanto, $W$ es positivo cuando el trabajo es realizado por el sistema y negativo cuando se realiza el trabajo en el sistema. Esta convención de signos se resume en la . La primera ley de la termodinámica se establece de la siguiente manera:
Primera ley de la Termodinámica
Asociado con cada estado de equilibrio de un sistema está su energía interna $E_{\textsf{int}}$. El cambio en la $E_{\textsf{int}}$ para cualquier transición entre dos estados de equilibrio es
$$ΔE_{\textsf{int}} = Q - W \tag{3.7}$$donde $Q$ y $W$ representan, respectivamente, el calor intercambiado por el sistema y el trabajo realizado por o sobre el sistema.
La primera ley es una declaración de la conservación de energía. Nos dice que un sistema puede intercambiar energía con su entorno mediante la transmisión de calor y la realización del trabajo. La energía neta intercambiada es entonces igual al cambio en la energía mecánica total de las moléculas del sistema (es decir, la energía interna del sistema). Por lo tanto, si un sistema está aislado, su energía interna debe permanecer constante.

Aunque $Q$ y $W$ dependen de la trayectoria termodinámica tomada entre dos estados de equilibrio, su diferencia $Q - W$ no lo hace. La muestra el diagrama $pV$ de un sistema que está haciendo la transición de A a B repetidamente a lo largo de diferentes trayectorias termodinámicas. A lo largo de la ruta 1, el sistema absorbe calor $Q_1$ y funciona $W_1$; a lo largo de la ruta 2, absorbe calor $Q_2$ y funciona $W_2$, y así sucesivamente. Los valores de $Q_i$ y $W_i$ pueden variar de una trayectoria a otra, pero tenemos
$$Q_1 − W_1 = Q_2 − W_2 = ... = Q_i − W_i = ... $$o
$$ΔE_{\textsf{int }1} = ΔE_{\textsf{int }2} = ... = Δ_{\textsf{int }i} = ...$$Es decir, el cambio en la energía interna del sistema entre $A$ y $B$ es independiente de la trayectoria. En el capítulo sobre la energía potencial y la conservación de la energía, nos encontramos con otra cantidad independiente de la trayectoria: el cambio en la energía potencial entre dos puntos arbitrarios en el espacio.
Este cambio representa el resultado negativo del trabajo realizado por una fuerza conservadora entre los dos puntos. La energía potencial es una función de las coordenadas espaciales, mientras que la energía interna es una función de las variables termodinámicas. Por ejemplo, podríamos escribir $E_{\textsf{int}}(T, p)$ para la energía interna.
Las funciones como la energía interna y la energía potencial se conocen como funciones de estado porque sus valores dependen únicamente del estado del sistema.
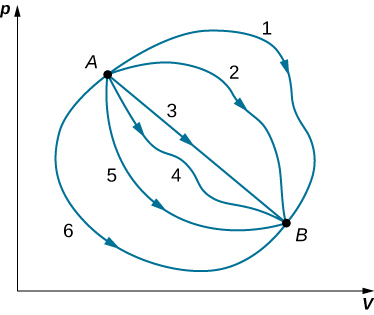
A menudo, la primera ley se usa en su forma diferencial, que es
$$dE_{\textsf{int}} = dQ - dW tag{3.8}$$Aquí $dE_{\textsf{int}}$ es un cambio infinitesimal en la energía interna cuando se intercambia una cantidad infinitesimal de calor $dQ$ con el sistema y una cantidad infinitesimal de trabajo $dW$ se realiza (signo positivo) o se da (signo negativo) al sistema.
Ejemplo 3.2
Cambios de estado y la primera ley
Durante un proceso termodinámico, un sistema pasa del estado $A$ al estado $B$, se suministra con $400 J$ de calor y realiza $100 J$ de trabajo. (a) Para esta transición, ¿cuál es el cambio del sistema en la energía interna? (b) Si el sistema luego se mueve del estado $B$ al estado $A$, ¿cuál es su cambio en la energía interna? (c) Si al pasar de $A$ a $B$ a lo largo de una trayectoria diferente, $W'_{AB} = 400 J$ de trabajo realizado en el sistema, ¿cuánto calor absorbe?
Estrategia
La primera ley de la termodinámica relaciona el cambio de energía interno, el trabajo realizado por el sistema y el calor transferido al sistema en una ecuación simple. La energía interna es una función del estado y, por lo tanto, se fija en cualquier punto dado independientemente de cómo el sistema llegue al estado.
Solución
a. Desde la primera ley, el cambio en la energía interna del sistema es
$$ΔE_{\textsf{int}AB} = Q_{AB} − W_{AB} = 400 J − 100 J = 300 J$$b. Considera una trayectoria cerrada que pasa por los estados $A$ y $B$. La energía interna es una función de estado, por lo que $ΔE_{\textsf{int}}$ es cero para una trayectoria cerrada. Así
$$ΔE_{\textsf{int}} = ΔE_{\textsf{int}AB} + ΔE_{\textsf{int}BA} = 0$$y
$$ΔE_{\textsf{int}AB} = −ΔE_{\textsf{int}BA}$$Obteniendo:
$$ΔE_{\textsf{int}BA} = −300 J$$c. El cambio en la energía interna es el mismo para cualquier camino, por lo que
$$ΔE_{\textsf{int}AB} = ΔE'_{\textsf{int}AB} = Q'_{AB} – W'_{AB}$$ $$300 j = Q'_{AB} – (−400 J)$$y el intercambio de calor es
$$Q'_{AB} = -100 J$$El signo negativo indica que el sistema pierde calor en esta transición.
Explicación
Cuando se considera un ciclo cerrado para la primera ley de la termodinámica, el cambio en la energía interna en todo la trayectoria es igual a cero. Si la fricción desempeñara un papel en este ejemplo, se obtendría menos trabajo de este calor agregado. El ejemplo 3.3 tiene en cuenta lo que sucede si la fricción desempeña un papel.
Observa que en el Ejemplo 3.2, no asumimos que las transiciones sean casi estáticas. Esto se debe a que la primera ley no está sujeta a dicha restricción. Describe las transiciones entre los estados de equilibrio, pero no se ocupa de los estados intermedios. El sistema no tiene que pasar solo por estados de equilibrio. Por ejemplo, si se hace explotar un gas en un recipiente de acero a una temperatura y presión bien definidas por medio de una chispa, parte del gas puede condensarse, diferentes moléculas de gas pueden combinarse para formar nuevos compuestos, y puede haber todo tipo de turbulencia en el contenedor, pero eventualmente, el sistema se establecerá en un nuevo estado de equilibrio.
Este sistema claramente no está en equilibrio durante su transición; sin embargo, su comportamiento todavía se rige por la primera ley porque el proceso comienza y termina con el sistema en estados de equilibrio.
Ejemplo 3.3
Pulido de un accesorio
Un maquinista pule un accesorio de cobre de $0,50 kg$ con un trozo de tela de esmeril durante $2,0$ minutos. Mueve la tela a través del accesorio a una velocidad constante de $1.0 m/s$ aplicando una fuerza de $20 N$ tangente a la superficie del accesorio.
(a) ¿Cuál es el trabajo total realizado en la instalación por el maquinista? (b) ¿Cuál es el aumento en la energía interna del accesorio? Supón que el cambio en la energía interna de la tela es insignificante y que no se intercambia calor entre la conexión y su entorno. (c) ¿Cuál es el aumento de la temperatura del accesorio?
Estrategia
La fuerza del maquinista en una distancia que se puede calcular a partir de la velocidad y el tiempo dado es el trabajo realizado en el sistema. El trabajo, a su vez, aumenta la energía interna del sistema. Esta energía puede interpretarse como el calor que eleva la temperatura del sistema a través de su capacidad calorífica. Ten cuidado con el signo de cada cantidad.
Solución
a. La potencia creada por una fuerza sobre un objeto o la velocidad a la que el maquinista realiza un trabajo de fricción en el accesorio es $\overrightarrow{\bold{F}} \cdot \overrightarrow{\bold{v}} = -Fv$. Por lo tanto, en un tiempo transcurrido $Δt(2.0 min)$, el trabajo realizado en el accesorio es
b. Por suposición, no se intercambia calor entre el accesorio y su entorno, por lo que la primera ley establece el cambio en la energía interna del accesorio:
$$ΔE_{\textsf{int}} = −W = 2.4 × 10^3 J$$c. Como $ΔE_{\textsf{int}}$ es independiente de la trayectoria, el efecto de $2.4 × 10^3 J$ de trabajo es el mismo que si se suministrara a la presión atmosférica mediante una transferencia de calor. Así,
$$2.4 × 10^3 J = mcΔT = (0.50 kg)(3.9×10^2 J/kg \cdot °C)ΔT$$y el aumento en la temperatura del accesorio es
$$ΔT = 12 °C$$donde hemos usado el valor para el calor específico del cobre, $c = 3.9 × 10^2 J/kg \cdot °C$.
Explicación
Si se liberara calor, el cambio en la energía interna sería menor y causaría un cambio de temperatura menor que el calculado en el problema.
 Comprueba tu aprendizaje 3.2
Comprueba tu aprendizaje 3.2
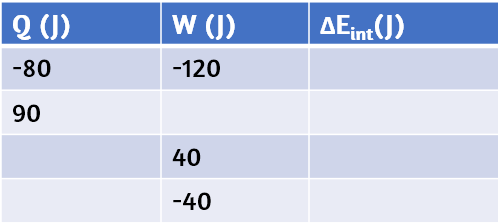
Ejemplo 3.4
Una transición de gas ideal entre dos estados
Considera las expansiones cuasiestáticas de un gas ideal entre los estados de equilibrio $A$ y $C$ de la figura 3.6. Si se agregan $515 J$ de calor al gas a medida que atraviesa la trayectoria $ABC$, ¿cuánto calor se requiere para la transición a lo largo de $ADC$? Supongamos que $p_1 = 2.10 × 10^5 N/m^2$, $p_2 = 1.05 × 10^5 N/m^2$, $V_1 = 2.25 × 10^{-3}m^3$ y $V_2 = 4.50 × 10^{-3} m^3$.
Estrategia
La diferencia en el trabajo realizado entre el proceso $ABC$ y el proceso $ADC$ es el área delimitada por $ABCD$. Debido a que el cambio de la energía interna (una función de estado) es el mismo para ambos procesos, la diferencia en el trabajo es, por lo tanto, la misma que la diferencia en el calor transferido al sistema.
Solución
Para la trayectoria $ABC$, el calor agregado es $Q_{ABC} = 515J$ y el trabajo realizado por el gas es el área bajo la trayectoria en el diagrama $pV$, que es
A lo largo de $ADC$, el trabajo realizado por el gas vuelve a ser el área bajo la trayectoria:
$$W_{ADC} = p_2(V_2 − V_1) = 236 J$$Luego, utilizando la estrategia que acabamos de describir, tenemos
$$Q_{ADC} − Q_{ABC} = W_{ADC} − W_{ABC}$$lo que lleva a
$$Q_{ADC} = Q_{ABC} + W_{ADC} − W_{ABC} = (515 + 236 − 473) J = 278 J$$Explicación
Los cálculos de trabajo en este problema se simplifican ya que no se realiza ningún trabajo a lo largo de $AD$ y $BC$ y a lo largo de $AB$ y $DC$; la presión es constante durante el cambio de volumen, por lo que el trabajo realizado es simplemente $pΔV$. También se podría haber usado una línea isotérmica, ya que hemos derivado el trabajo para un proceso isotérmico como $W = nRTln(V_2/V_1)$.
Ejemplo 3.5
Expansión isotérmica de un gas ideal
Se agrega calor a $1 mol$ de un gas monoatómico ideal confinado a un cilindro con un pistón móvil en un extremo. El gas se expande cuasi-estáticamente a una temperatura constante de $300 K$ hasta que su volumen aumenta de $V$ a $3V$. (a) ¿Cuál es el cambio en la energía interna del gas? (b) ¿Cuánto trabajo hace el gas? (c) ¿Cuánto calor se agrega al gas?
Estrategia
(a) Debido a que el sistema es un gas ideal, la energía interna solo cambia cuando cambia la temperatura. (b) El calor agregado al sistema es, por lo tanto, puramente utilizado para hacer el trabajo que se ha calculado en el capítulo sobre Trabajo, Calor y Energía Interna. (c) Finalmente, la primera ley de la termodinámica se puede usar para calcular el calor agregado al gas.
Solución
a. Vimos en la sección anterior que la energía interna de un gas monoatómico ideal es una función solo de la temperatura. Dado que $ΔT = 0$, para este proceso, $ΔE_{\textsf{int}} = 0$.
b. La expansión isotérmica cuasi estática de un gas ideal se consideró en la sección anterior y se encontró que era
$$W = nRT_1n\frac{V_2}{V_1} = nRT_1n\frac{3V}{V}$$ $$W = (1.00 mol)(8.314 J/K \cdot mol)(300 K)(ln3) = 2.74 × 10^3 J$$c. Con los resultados de las partes (a) y (b), podemos usar la primera ley para determinar el calor agregado:
$$ΔE_{\textsf{int}} = Q - W = 0$$lo que lleva a
$$Q = W = 2,74 × 10^3 J$$Explicación
Un proceso isotérmico no tiene cambios en la energía interna. Basado en eso, la primera ley de la termodinámica se reduce a $Q = W$.
 Comprueba tu aprendizaje 3.3
Comprueba tu aprendizaje 3.3
Ejemplo 3.6
Vaporizando el agua
Cuando $1,00 g$ de agua a $100 °C$ cambia del líquido a la fase gaseosa a la presión atmosférica, su cambio de volumen es de $1,67 × 10^{-3} m^3.$ (a) ¿Cuánto calor se debe agregar para vaporizar el agua? (b) ¿Cuánto trabajo realiza el agua contra la atmósfera en su expansión? (c) ¿Cuál es el cambio en la energía interna del agua?
Estrategia
Primero podemos determinar cuánto calor se necesita del calor latente de vaporización del agua. A partir del cambio de volumen, podemos calcular el trabajo realizado desde $W = pΔV$ porque la presión es constante. Entonces, la primera ley de la termodinámica nos proporciona el cambio en la energía interna.
Solución
a. Con $L_v$ representando el calor latente de vaporización, el calor requerido para vaporizar el agua es
$$Q = mL_v = (1.00 g)(2.26 × 10^3 J/g) = 2.26 × 10^3J$$b. Dado que la presión en el sistema es constante a $1.00atm = 1.01 × 10^5 N/m^2$, el trabajo realizado por el agua mientras se vaporiza es
c. Desde la primera ley, la energía térmica del agua durante su vaporización cambia por
$$ΔE_{\textsf{int}} = Q - W = 2.26 × 10^3 J - 169 J = 2.09 × 10^3 J$$Explicación
Notamos que en la parte (c), vemos un cambio en la energía interna, sin embargo, no hay cambio en la temperatura. Los gases ideales que no están experimentando cambios de fase tienen la energía interna proporcional a la temperatura. La energía interna, en general, es la suma de toda la energía en el sistema.
 Comprueba tu aprendizaje 3.4
Comprueba tu aprendizaje 3.4
Al resolver problemas mecánicos, aislamos el cuerpo bajo consideración, analizamos las fuerzas externas que actúan sobre él y luego usamos las leyes de Newton para predecir su comportamiento. En termodinámica, tomamos un enfoque similar. Comenzamos identificando la parte del universo que deseamos estudiar, también se conoce como nuestro sistema (Definimos un sistema al principio de este capítulo como cualquier cosa cuyas propiedades nos interesen, puede ser un solo átomo o toda la Tierra).
Una vez que se selecciona nuestro sistema, determinamos cómo interactúa el entorno o alrededores con el sistema. Finalmente, con la interacción entendida, estudiamos el comportamiento térmico del sistema con la ayuda de las leyes de la termodinámica.
El comportamiento térmico de un sistema se describe en términos de variables termodinámicas. Para un gas ideal, estas variables son la presión, el volumen, la temperatura y la cantidad de moléculas o moles del gas. Los diferentes tipos de sistemas generalmente se caracterizan por diferentes conjuntos de variables. Por ejemplo, las variables termodinámicas para una banda elástica estirada son tensión, longitud, temperatura y masa.
El estado de un sistema puede cambiar como resultado de su interacción con el entorno. El cambio en un sistema puede ser rápido o lento y grande o pequeño. La forma en que un estado de un sistema puede cambiar de un estado inicial a un estado final se denomina proceso termodinámico. Para fines analíticos en termodinámica, es útil dividir los procesos como cuasiestáticos o no cuasiestáticos, como explicamos ahora.
Un proceso cuasiestático se refiere a un proceso idealizado o imaginado donde el cambio de estado se hace infinitesimalmente lento, de modo que en cada instante se puede asumir que el sistema está en un equilibrio termodinámico consigo mismo y con el entorno.
Por ejemplo, imagina calentar $1 kg$ de agua desde una temperatura de $20 °C$ a $21 °C$ a una presión constante de $1$ atmósfera. Para calentar el agua muy lentamente, podemos imaginar colocar el recipiente con agua en un baño María que pueda calentarse lentamente de modo que la temperatura del baño pueda elevarse infinitesimalmente lentamente de $20 °C$ a $21 °C$.
Si ponemos $1 kg$ de agua a $20 °C$ directamente en un baño a $21 °C$, la temperatura del agua aumentará rápidamente a $21 °C$ de una manera no cuasi estática.
Los procesos cuasiestáticos se realizan con la suficiente lentitud para que el sistema permanezca en equilibrio termodinámico en cada instante, a pesar de que el sistema cambia con el tiempo. El equilibrio termodinámico del sistema es necesario para que el sistema tenga valores bien definidos de propiedades macroscópicas tales como la temperatura y la presión del sistema en cada instante del proceso. Por lo tanto, los procesos cuasiestáticos pueden mostrarse como rutas bien definidas en el espacio de estados del sistema.
Dado que los procesos cuasiestáticos no se pueden realizar por completo para cualquier cambio finito del sistema, todos los procesos en la naturaleza son no cuasiestáticos. Ejemplos de procesos cuasiestáticos y no cuasiestáticos se muestran en la . A pesar del hecho de que todos los cambios finitos deben ocurrir esencialmente no cuasi-estáticamente en alguna etapa del cambio, podemos imaginar realizar infinitamente muchos procesos cuasiestáticos correspondientes a cada proceso cuasiestático. Dado que los procesos cuasi-estáticos se pueden analizar analíticamente, en su mayoría estudiamos procesos cuasiestáticos en este libro. Ya hemos visto que en un proceso cuasiestático el trabajo por un gas viene dado por $pdV$.
Un proceso isotérmico es un cambio en el estado del sistema a una temperatura constante. Este proceso se lleva a cabo manteniendo el sistema en equilibrio térmico con un gran baño de calor durante el proceso. Recuerda que un baño de calor es un sistema ideal "infinitamente" grande cuya temperatura no cambia. En la práctica, la temperatura de un baño finito se controla agregando o eliminando una cantidad finita de energía, según sea el caso.
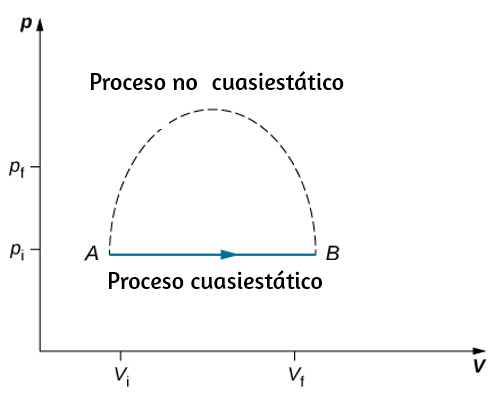
Como ilustración de un proceso isotérmico, considere un cilindro de gas con un pistón móvil sumergido en un gran tanque de agua cuya temperatura se mantiene constante. Dado que el pistón se puede mover libremente, la presión dentro de $P_{\textsf{in}}$ se equilibra con la presión fuera de $P_{\textsf{out}}$ por algunos pesos en el pistón, como en la
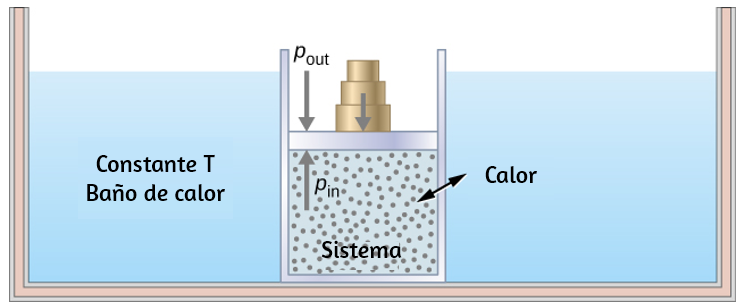
A medida que se eliminan los pesos en el pistón, se desarrolla un desequilibrio de fuerzas en el pistón. La fuerza neta no nula en el pistón haría que el pistón se acelere, lo que da como resultado un aumento en el volumen. La expansión del gas enfría el gas a una temperatura más baja, lo que hace posible que el calor ingrese desde el baño de calor al sistema hasta que la temperatura del gas se reinicie a la temperatura del baño de calor.
Si los pesos se eliminan en pasos infinitesimales, la presión en el sistema disminuye infinitamente lentamente. De esta forma, se puede llevar a cabo un proceso isotérmico casi estáticamente. Una línea isotérmica en un diagrama $(p, V)$ está representada por una línea curva desde el punto inicial $A$ hasta el punto final $B$, como se ve en la . Para un gas ideal, un proceso isotérmico es hiperbólico, ya que para un gas ideal a temperatura constante: $p α 1/V$.
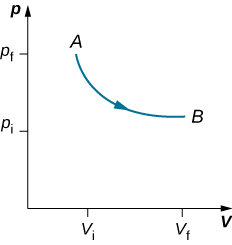
Un proceso isotérmico estudiado en este capítulo se realiza cuasi-estáticamente, ya que para ser isotérmico en todo el cambio de volumen, debe ser capaz de indicar la temperatura del sistema en cada paso, lo cual es posible solo si el sistema está en equilibrio térmico continuamente. El sistema debe salir del equilibrio para que cambie el estado, pero para los procesos cuasi-estáticos, imaginamos que el proceso se lleva a cabo en pasos infinitesimales, de modo que estas desviaciones del equilibrio puedan hacerse tan breves y tan pequeñas como queramos.
Otros procesos cuasiestáticos de interés para los gases son los procesos isobáricos e isocóricos. Un proceso isobárico es un proceso donde la presión del sistema no cambia, mientras que un proceso isocórico es un proceso donde el volumen del sistema no cambia.
En un proceso adiabático, el sistema está aislado de su entorno, de modo que, aunque el estado del sistema cambia, no se permite que el calor entre o salga del sistema, como se ve en la . Se puede llevar a cabo un proceso adiabático de forma cuasiestática o no cuasiestática. Cuando un sistema se expande adiabáticamente, debe funcionar contra el mundo exterior y, por lo tanto, su energía disminuye, lo que se refleja en la disminución de la temperatura del sistema. Una expansión adiabática conduce a una disminución de la temperatura, y una compresión adiabática conduce a un aumento de la temperatura.
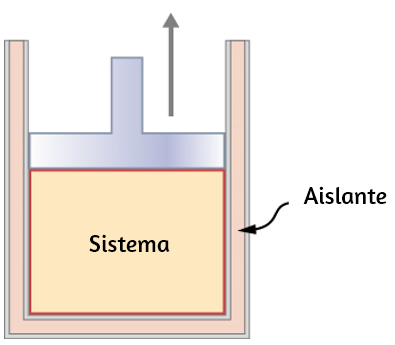
Decimos que un sistema pasa por un proceso cíclico si el estado del sistema al final es el mismo que el estado al principio. Por lo tanto, las propiedades de estado como temperatura, presión, volumen y energía interna del sistema no cambian en un ciclo completo:
$$ΔE_{\textsf{int}} = 0$$Cuando la primera ley de la termodinámica se aplica a un proceso cíclico, obtenemos una relación simple entre el calor en el sistema y el trabajo realizado por el sistema durante el ciclo:
$$Q = W (\textsf{proceso cíclico})$$Los procesos termodinámicos también se distinguen por ser reversibles o no. Un proceso reversible es uno que se puede hacer para volver sobre su trayectoria mediante cambios diferenciales en el entorno. Tal proceso, por lo tanto, también debe ser cuasiestático. Ten en cuenta, sin embargo, que un proceso cuasiestático no es necesariamente reversible, ya que puede haber fuerzas disipativas involucradas.
Por ejemplo, si ocurriera fricción entre el pistón y las paredes del cilindro que contiene el gas, la energía perdida por fricción nos impediría reproducir los estados originales del sistema.
Consideramos varios procesos termodinámicos:
También se producen muchos otros procesos que no encajan en ninguna de estas cuatro categorías.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, puedes configurar tu propio proceso en un diagrama $pV$. Observa si puedes calcular los valores predichos por la simulación para el calor, el trabajo y el cambio en la energía interna.
Simulación de un Diagrama $PV$. Arrastra los puntos $A$, $B$, $C$ y $D$ para explorar diferentes ciclos. Verifica la tabla de datos para ver el cambio en la energía interna ($ΔU$), el trabajo realizado en el gas ($W$) y el calor agregado al gas ($Q$). También se calcula la eficiencia del ciclo.
Aprendimos sobre el calor específico y la capacidad de calor molar en el apartado de temperatura y calor; sin embargo, no hemos considerado un proceso en el que se agregue calor. Hacemos eso en esta sección. Primero, examinamos un proceso donde el sistema tiene un volumen constante, luego lo contrastamos con un sistema a presión constante y mostramos cómo se relacionan sus calores específicos.
Comencemos mirando la , que muestra dos recipientes $A$ y $B$, cada uno con $1 mol$ del mismo tipo de gas ideal a una temperatura $T$ y un volumen $V$. La única diferencia entre los dos recipientes es que el pistón en la parte superior de $A$ es fijo, mientras que el que está en la parte superior de $B$ es libre de moverse contra una presión externa constante $p$. Ahora consideramos qué ocurre cuando la temperatura del gas en cada recipiente aumenta lentamente a $T + dT$ con la adición de calor.
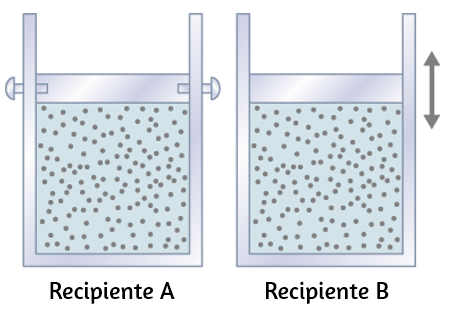
Como el pistón del recipiente $A$ está fijo, el volumen del gas encerrado no cambia. En consecuencia, el gas no funciona, y tenemos desde la primera ley
$$dE_{\textsf{int}} = dQ - dW = dQ$$Representamos el hecho de que el calor se intercambia a volumen constante al escribir
$$dQ = C_VdT \tag{3.9}$$donde $C_V$ es la capacidad de calor molar a volumen constante del gas. Además, dado que $dE_{\textsf{int}} = dQ$ para este proceso en particular,
$$dE_{\textsf{int}} = C_VdT$$Obtuvimos esta ecuación suponiendo que el volumen del gas es fijo. Sin embargo, la energía interna es una función de estado que depende únicamente de la temperatura de un gas ideal. Por lo tanto, $dE_{\textsf{int}} = C_VdT$ proporciona el cambio en la energía interna de un gas ideal para cualquier proceso que implique un cambio de temperatura $dT$.
Cuando el gas en el recipiente $B$ se calienta, se expande contra el pistón móvil y funciona $dW = pdV$. En este caso, el calor se agrega a presión constante, y escribimos
$$dQ = C_pdT$$donde $C_p$ es la capacidad de calor molar a presión constante del gas. Además, dado que el gas ideal se expande contra una presión constante,
$$d(pV) = d(RT)$$se convierte
$$pdV = RdT$$Finalmente, insertando las expresiones para $dQ$ y $pdV$ en la primera ley, obtenemos
$$dE_{\textsf{int}} = dQ - pdV = (C_p - R)dT$$Hemos encontrado una marca para ambos procesos isocóricos y isobáricos. Debido a que la energía interna de un gas ideal depende solo de la temperatura, $dE_{\textsf{int}}$ debe ser el mismo para ambos procesos. Así,
$$C_VdT = (C_p - R)dT$$y
La derivación de la Ecuación 3.10 se basó solo en la ley de los gases ideales. En consecuencia, esta relación es aproximadamente válida para todos los gases diluidos, ya sean monoatómicos como el $He$, diatómicos como el $O_2$ o poliatómicos como el $CO_2$ o el $NH_3$.
En el capítulo anterior, encontramos la capacidad de calor molar de un gas ideal bajo un volumen constante como:
$$C_V = \frac{d}{2}R$$donde $d$ es el número de grados de libertad de una molécula en el sistema. La muestra las capacidades de calor molar de algunos gases ideales diluidos a temperatura ambiente. Las capacidades de calor de los gases reales son algo más altas que las predichas por las expresiones de $C_V$ y $C_p$ dadas en la ecuación 3.10. Esto indica que el movimiento vibratorio en las moléculas poliatómicas es significativo, incluso a temperatura ambiente. Sin embargo, la diferencia en las capacidades de calor molar, $C_p - C_V$, es muy cercana a $R$, incluso para los gases poliatómicos.
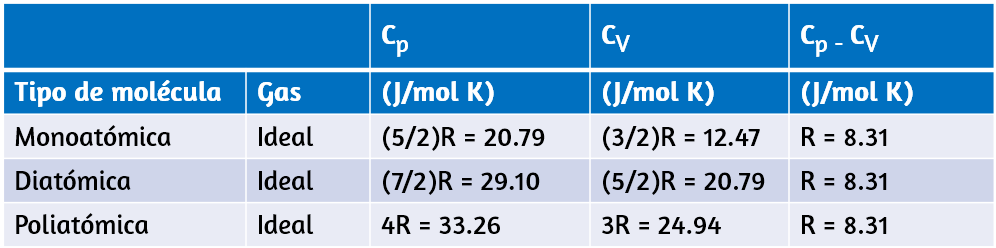
Cuando un gas ideal se comprime adiabáticamente ($Q = 0$), el trabajo está hecho y su temperatura aumenta, en una expansión adiabática, el gas trabaja y su temperatura baja. En realidad, las compresiones adiabáticas se producen en los cilindros de un automóvil, donde las compresiones de la mezcla de gas y aire tienen lugar tan rápidamente que no hay tiempo para que la mezcla intercambie calor con su entorno. Sin embargo, debido a que se trabaja en la mezcla durante la compresión, su temperatura aumenta significativamente. De hecho, los aumentos de temperatura pueden ser tan grandes que la mezcla puede explotar sin la adición de una chispa. Dichas explosiones, dado que no están cronometradas, hacen que el automóvil funcione mal, por lo general "golpea".
Debido a que la temperatura de ignición aumenta con el octano de gasolina, una forma de superar este problema es usar gasolina de alto octanaje.
Otro proceso adiabático interesante es la expansión libre de un gas. La muestra un gas confinado por una membrana a un lado de un contenedor con aislamiento térmico de dos compartimentos. Cuando se pincha la membrana, el gas se precipita en el lado vacío del contenedor, expandiéndose así libremente. Debido a que el gas se expande "contra un vacío" ($p = 0$), no trabaja, y debido a que el recipiente está aislado térmicamente, la expansión es adiabática. Con $Q = 0$ y $W = 0$ en la primera ley, $ΔE_{\textsf{int}} = 0$, entonces $E_{\textsf{int }i} = E_{\textsf{int }f}$ para la expansión libre.
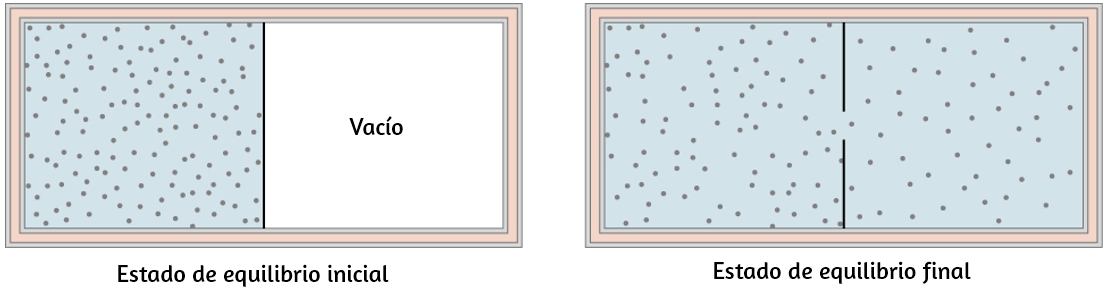
Si el gas es ideal, la energía interna depende solo de la temperatura. Por lo tanto, cuando un gas ideal se expande libremente, su temperatura no cambia.
En la se representa una expansión adiabática cuasiestática de un gas ideal, que muestra un cilindro aislado que contiene $1 mol$ de un gas ideal.
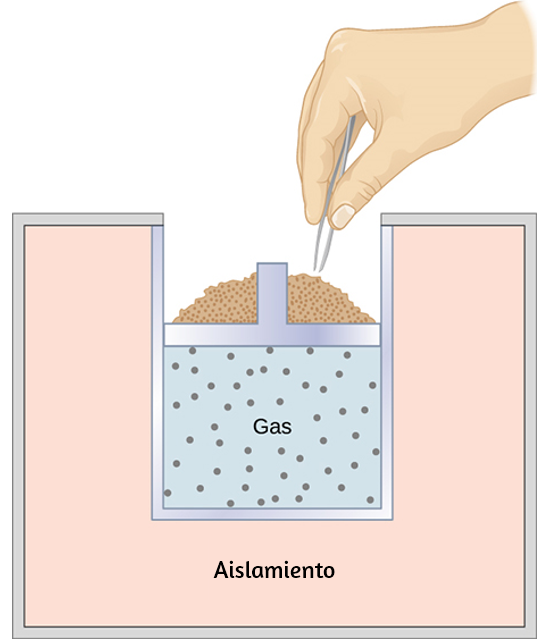
El gas está hecho para expandirse casi estáticamente al eliminar un grano de arena a la vez desde la parte superior del pistón. Cuando el gas se expande por $dV$, el cambio en su temperatura es $dT$. El trabajo realizado por el gas en la expansión es $dW = pdV$ y $dQ = 0$, porque el cilindro está aislado; y el cambio en la energía interna del gas es, a partir de la Ecuación 3.9, $dE_{\textsf{int}} = C_VdT$. Por lo tanto, desde la primera ley,
$$C_VdT = 0 - pdV = -pdV$$Así que
$$dT = -\frac{pdV}{C_V}$$Además, por $1 mol$ de un gas ideal,
$$d(pV) = d(RT)$$así que
$$pdV + Vdp = RdT$$y
$$dT = \frac{pdV + Vdp}{R}$$Ahora tenemos dos ecuaciones para $dT$. Al equipararlos, encontramos que
$$C_VVdp + (C_V + R)pdV = 0$$Ahora, dividimos esta ecuación por $pV$ y usamos $C_p = C_V + R$. Entonces nos quedamos con
$$C_V\frac{dp}{p} + C_p\frac{dV}{V} = 0$$que se convierte en
$$\frac{dp}{p} + γ\frac{dV}{V}$$donde definimos $γ$ como la relación de las capacidades de calor molar:
Entonces:
$$\int \frac{dp}{p} + γ \int \frac{dV}{V}$$Obtenemos:
$$lnp + γlnV = constante$$Finalmente, usando $ln(A^x) = xlnA$ y $lnAB = lnA + lnB$, podemos escribir
Esta ecuación es la condición que debe ser obedecida por un gas ideal en un proceso adiabático cuasiestático. Por ejemplo, si un gas ideal realiza una transición adiabática cuasiestática desde un estado con presión y volumen $p_1$ y $V_1$ a un estado con $p_2$ y $V_2$, entonces debe ser cierto que $p_1V_1^γ = p_2V_2^γ$.
La condición adiabática de la Ecuación 3.12 puede escribirse en términos de otros pares de variables termodinámicas combinándola con la ley de los gases ideales. Al hacer esto, encontramos que
$$p^{1−γ} T^γ = constante \tag{3.13}$$y
$$TV^{γ-1} \tag{3.14}$$En el diagrama $pV$ de la se representa una expansión adiabática reversible de un gas ideal. La pendiente de la curva en cualquier punto es
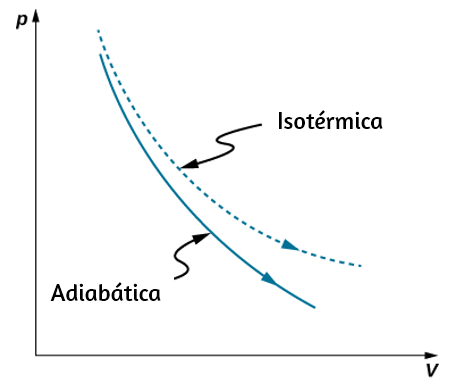
La curva discontinua que se muestra en este diagrama $pV$ representa una expansión isotérmica donde $T$ (y, por lo tanto, $pV$) es constante. La pendiente de esta curva es útil cuando consideramos la segunda ley de la termodinámica en el próximo capítulo. Esta pendiente es
$$\frac{dp}{dV} = \frac{d}{dV}\frac{nRT}{V} = -\frac{p}{V}$$Debido a que $γ > 1$, la curva isotérmica no es tan pronunciada como la de la expansión adiabática.
Ejemplo 3.7
Compresión de un gas ideal en un motor de automóvil
El vapor de gasolina se inyecta en el cilindro de un motor de automóvil cuando el pistón está en su posición expandida. La temperatura, presión y volumen de la mezcla de gas-aire resultante son $20 °C$, $1.00 × 10^5 N/m^2$ y $240 cm^3$, respectivamente. La mezcla se comprime adiabáticamente a un volumen de $40 cm^3$. Ten en cuenta que en la operación real de un motor de automóvil, la compresión no es cuasiestática, aunque estamos haciendo esa suposición aquí. (a) ¿Cuál es la presión y la temperatura de la mezcla después de la compresión? (b) ¿Cuánto trabajo realiza la mezcla durante la compresión?
Estrategia
Debido a que estamos modelando el proceso como una compresión adiabática cuasiestática de un gas ideal, tenemos $pV^γ = constante$ y $pV = nRT$. El trabajo necesario se puede evaluar con $$W = \int_{V_1}^{V_2} pdV$$
Solución
a. Para una compresión adiabática tenemos
$$p_2 = p_1(V_1/V_2)^γ$$entonces después de la compresión, la presión de la mezcla es
$$p_2 = (1.00 × 10^5 N/m^2) \left( \frac{240 × 10^{-6}m^3}{40 × 10^{-6}m^3} \right)^{1.40} = 1.23 × 10^6 N/m^2$$Según la ley de los gases ideales, la temperatura de la mezcla después de la compresión es
$$\begin{align*} T_2 &= \frac{p_2V_2}{p_1V_1}T_1 \\ &= \frac{(1.23 × 10^6 N/m^2)(40 × 10^{-6} m^3)}{(1.00 × 10^5 N/m^2)(240 × 10^{-6} m^3)} \cdot 293 K \\ &= 600 K = 328 °C \end{align*}$$b. El trabajo realizado por la mezcla durante la compresión es
$$W = \int_{V_1}^{V_2} pdV$$Con la condición adiabática de la Ecuación 3.12, podemos escribir $p$ como $K/V^γ$, donde $K = p_1V_1^γ = p_2V_2^γ$. El trabajo es por lo tanto
$$\begin{align*} W &= \int_{V_1}^{V_2} \frac{K}{2}V^γ \\ &= \frac{K}{1-γ} \left(\frac{1}{V_2^{γ-1}} - \frac{1}{V_1^{γ-1}} \right) \\ &= \frac{1}{1-γ} \left(\frac{p_{V_2^γ}}{V_2^{γ-1}} - \frac{p_{V_1^γ}}{V_1^{γ-1}} \right) \\ &= \frac{1}{1-γ}(p_2V_2 − p_1V_1) \\ &= \frac{1}{1 - 1.40}[(1.23 × 10^6 N/m^2)(40 × 10^{-6} m^3) \\ &−(1.00 × 10^5 N/m^2)(240 × 10^{-6} m^3)] \\ &= −63 J \end{align*}$$Explicación
El signo negativo en el trabajo realizado indica que el pistón trabaja en la mezcla de gas y aire. El motor no trabajaría si la mezcla de gas y aire trabajara en el pistón.
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, se presenta un proceso adiabático, donde la presión y el volumen están relacionados por la ecuación $PV^{5/3} = constante$.
El valor de la constante, que es diferente para diferentes proceso, la hemos llamado $k$, entonces la función que da la línea de un proceso adiabático (línea entre $A$ y $B$) está dada por $y = k/x^{5/3}$. Usa los controles para observar diferentes procesos.

De acuerdo con la primera ley de la termodinámica, los únicos procesos que pueden ocurrir son los que conservan energía. Pero esta no puede ser la única restricción impuesta por la naturaleza, porque muchos procesos termodinámicos aparentemente posibles que conservarían energía no ocurren. Por ejemplo, cuando dos cuerpos están en contacto térmico, el calor nunca fluye del cuerpo más frío al más cálido, aunque esto no está prohibido por la primera ley. Entonces, algunos otros principios termodinámicos deben controlar el comportamiento de los sistemas físicos.
Uno de estos principios es la segunda ley de la termodinámica, que limita el uso de energía dentro de una fuente. La energía no puede pasar arbitrariamente de un objeto a otro, del mismo modo que no podemos transferir el calor de un objeto frío a uno caliente sin hacer ningún trabajo.
No podemos separar la crema del café sin un proceso químico que cambie las características físicas del sistema o su entorno. No podemos utilizar la energía interna almacenada en el aire para propulsar un automóvil, o usar la energía del océano para hacer funcionar un barco, sin perturbar algo alrededor de ese objeto.
En el capítulo que cubre la primera ley de la termodinámica, comenzamos nuestra discusión con una broma de CP Snow que afirmaba que la primera ley significa "no se puede ganar". Parafraseó la segunda ley como "no se puede alcanzar el punto de equilibrio, excepto en un día muy frío". A menos que estés en cero kelvin, no puedes convertir el $100$% de la energía térmica en trabajo. Comenzaremos discutiendo los procesos espontáneos y explicaremos por qué algunos procesos requieren que se produzca un trabajo, incluso si la energía se hubiera conservado.
Considera un gas ideal que se sostiene en la mitad de un contenedor aislado térmicamente por una pared en el medio del contenedor. La otra mitad del contenedor está en vacío sin moléculas adentro. Ahora, si quitamos la pared del medio rápidamente, el gas se expande y llena todo el contenedor inmediatamente, como se muestra en la .
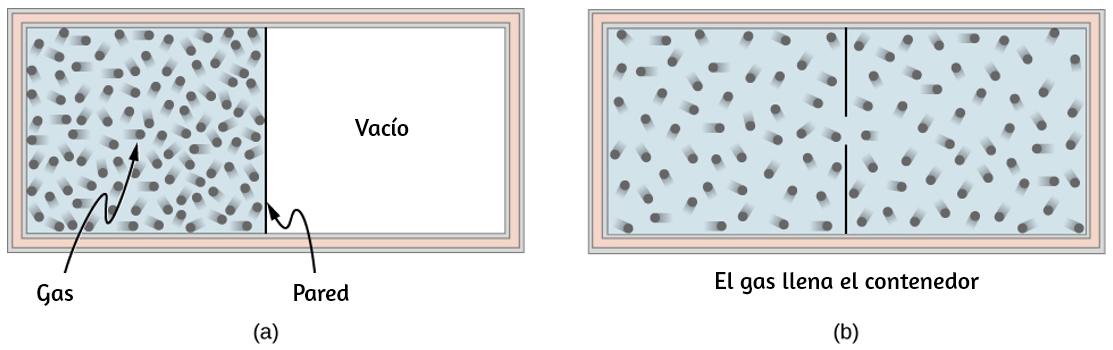
Debido a que la mitad del contenedor está bajo vacío antes de que el gas se expanda allí, no esperamos que el sistema haga ningún trabajo, es decir, $W = 0$, porque no se ejerce ninguna fuerza desde el vacío sobre el gas durante la expansión.
Si el contenedor está aislado térmicamente del resto del entorno, tampoco esperamos ninguna transferencia de calor al sistema, por lo que $Q = 0$. Entonces, la primera ley de la termodinámica conduce al cambio de la energía interna del sistema,
$$ΔE_{\textsf{int}} = Q - W = 0$$Para un gas ideal, si la energía interna no cambia, entonces la temperatura permanece igual. Por lo tanto, la ecuación de estado del gas ideal nos da la presión final del gas, $p = nRT/V = p_0/2$, donde $p_0$ es la presión del gas antes de la expansión. El volumen se duplica y la presión se reduce a la mitad, pero nada más parece haber cambiado durante la expansión.
Toda esta discusión se basa en lo que hemos aprendido hasta ahora y tiene sentido. Esto es lo que nos desconcierta: ¿pueden todas las moléculas retroceder a la mitad original del contenedor en algún momento futuro?
Nuestra intuición nos dice que esto será muy improbable, a pesar de que nada de lo que hemos aprendido hasta ahora impide que ocurra tal evento, independientemente de cuán pequeña sea la probabilidad. Lo que realmente estamos preguntando es si la expansión en la mitad del vacío del contenedor es reversible.
Un proceso reversible es un proceso en el que el sistema y el entorno se pueden restaurar exactamente en los mismos estados iniciales en los que se encontraban antes de que ocurriera el proceso, si retrocedimos a lo largo de la ruta del proceso.
La condición necesaria para un proceso reversible es, por lo tanto, el requisito cuasiestático. Ten en cuenta que es bastante fácil restaurar un sistema a su estado original; la parte difícil es tener su entorno restaurado a su estado original al mismo tiempo. Por ejemplo, en el caso de un gas ideal que se expande al vacío al doble de su volumen original, podemos empujarlo fácilmente hacia atrás con un pistón y restaurar su temperatura y presión eliminando algo de calor del gas. El problema es que no podemos hacerlo sin cambiar algo en su entorno, como descargar algo de calor allí.
Un proceso reversible es realmente un proceso ideal que rara vez sucede. Podemos hacer que ciertos procesos sean casi reversibles y, por lo tanto, usar las consecuencias de los procesos reversibles correspondientes como punto de partida o referencia. En realidad, casi todos los procesos son irreversibles, y algunas propiedades del entorno se alteran cuando se restauran las propiedades del sistema. La expansión de un gas ideal, como acabamos de describir, es irreversible porque el proceso ni siquiera es cuasiestático, es decir, no se encuentra en un estado de equilibrio en ningún momento de la expansión.
Desde el punto de vista microscópico, una partícula descrita por la segunda ley de Newton puede ir hacia atrás si volteamos la dirección del tiempo.
Pero este no es el caso, en términos prácticos, en un sistema macroscópico con más de 1023 partículas o moléculas, donde numerosas colisiones entre estas moléculas tienden a borrar cualquier rastro de memoria de la trayectoria inicial de cada una de las partículas. Por ejemplo, podemos estimar la posibilidad de que todas las partículas en el gas expandido vuelvan a la mitad original del contenedor, pero la edad actual del universo todavía no es lo suficientemente larga como para que ocurra ni siquiera una vez.
Un proceso irreversible es lo que encontramos en la realidad casi todo el tiempo. El sistema y su entorno no se pueden restaurar a sus estados originales al mismo tiempo. Porque esto es lo que sucede en la naturaleza, también se llama un proceso natural. El signo de un proceso irreversible proviene del gradiente finito entre los estados que ocurren en el proceso real. Por ejemplo, cuando el calor fluye de un objeto a otro, hay una diferencia de temperatura finita (gradiente) entre los dos objetos. Más importante aún, en cualquier momento dado del proceso, el sistema probablemente no esté en equilibrio o en un estado bien definido. Este fenómeno se llama irreversibilidad.
Veamos otro ejemplo de irreversibilidad en los procesos térmicos. Considera dos objetos en contacto térmico: uno a temperatura $T_1$ y el otro a temperatura $T_2 > T_1$, como se muestra en la .
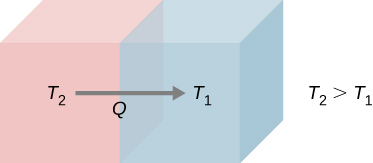
Sabemos por experiencia personal común que el calor fluye de un objeto más caliente a uno más frío. Por ejemplo, cuando sostenemos algunos pedazos de hielo en nuestras manos, sentimos frío porque el calor ha dejado nuestras manos en el hielo. Lo opuesto es cierto cuando sostenemos un extremo de una varilla de metal mientras mantenemos el otro extremo sobre el fuego. En base a todos los experimentos que se han realizado sobre la transferencia de calor espontánea, la siguiente declaración resume el principio rector:
Segunda ley de Termodinámica (declaración de Clausius)
El calor nunca fluye espontáneamente de un objeto más frío a un objeto más caliente.
Esta declaración resulta ser una de varias maneras diferentes de establecer la segunda ley de la termodinámica. La forma de esta afirmación se atribuye al físico alemán Rudolf Clausius (1822-1888) y se la conoce como la declaración de Clausius de la segunda ley de la termodinámica. La palabra "espontáneamente" significa que ningún otro esfuerzo ha sido realizado por un tercero, o que no sea el objeto más frío ni más caliente. Presentaremos algunas otras afirmaciones importantes de la segunda ley y demostraremos que implican la una a la otra. De hecho, todos los enunciados diferentes de la segunda ley de la termodinámica pueden mostrarse equivalentes, y todos conducen a la irreversibilidad del flujo de calor espontáneo entre objetos macroscópicos de un gran número de moléculas o partículas.
Los procesos isotérmicos y adiabáticos bosquejados en un gráfico pV (discutido en La primera ley de la termodinámica) son reversibles en principio porque el sistema está siempre en un estado de equilibrio en cualquier punto de los procesos y puede avanzar o retroceder a lo largo de las curvas dadas. Otros procesos idealizados pueden representarse mediante curvas $pV$. La resume los procesos reversibles más comunes.

Una máquina térmica es un dispositivo utilizado para extraer calor de una fuente y luego convertirlo en un trabajo mecánico que se utiliza para todo tipo de aplicaciones. Por ejemplo, una máquina de vapor en un tren antiguo puede producir el trabajo necesario para conducir el tren. Varias preguntas surgen de la construcción y aplicación de máquinas térmicas. Por ejemplo, ¿cuál es el porcentaje máximo del calor extraído que se puede usar para hacer el trabajo? Esto resulta ser una pregunta que solo puede ser respondida a través de la segunda ley de la termodinámica.
La segunda ley de la termodinámica se puede establecer formalmente de varias maneras.
Inicialmente, observa e interactúa con una escena interactiva del Proyecto Un_100 de la Red Descartes.
A través de una conversación con un tutor digital, y la observación y el análisis simultáneos de una máquina térmica, revisarás las leyes fundamentales de la termodinámica y de los gases ideales.
En el diálogo, analizarás las distintas etapas del ciclo de la máquina de calor: compresión adiabática, calentamiento isóbaro, expansión adiabática y enfriamiento isóbaro. Tendrás que hacer una serie de predicciones con base en tu conocimiento. Al final entenderás cómo es que la máquina convierte calor en trabajo, y que no se pierde energía en ninguna etapa del ciclo de la misma.
Una afirmación presentada hasta ahora es acerca de la dirección del flujo de calor espontáneo, conocida como la declaración de Clausius. Un par de otras declaraciones se basan en máquinas térmicas. Cada vez que consideramos las máquinas térmicas y los dispositivos asociados, como refrigeradores y bombas de calor, no utilizamos la convención de signos normal para el calor y el trabajo. Para mayor comodidad, suponemos que los símbolos $Q_h$, $Q_c$ y $W$ representan solo las cantidades de calor transferido y trabajo entregado, independientemente de lo que sean los donantes o los receptores. Si el calor ingresa o sale de un sistema y el trabajo se realiza por un sistema se indica con los signos adecuados delante de los símbolos y con las direcciones de las flechas en los diagramas.
Resulta que necesitamos más de una fuente de calor para construir una máquina térmica. Volveremos sobre este punto más adelante en el capítulo, cuando comparemos diferentes enunciados de la segunda ley de la termodinámica. Por el momento, suponemos que se construye una máquina térmica entre una fuente de calor (depósito de alta temperatura o depósito caliente) y un disipador de calor (depósito de baja temperatura o depósito frío), representado esquemáticamente en la . La máquina absorbe calor $Q_h$ de una fuente de calor (depósito caliente) de temperatura Kelvin $T_h$, utiliza parte de esa energía para producir trabajo útil $W$, y luego descarta la energía restante como calor $Q_c$ en un disipador de calor (depósito frío) de temperatura Kelvin $T_c$. Las plantas de energía y los motores de combustión interna son ejemplos de motores de calor o máquinas térmicas. Las plantas de energía usan vapor producido a alta temperatura para impulsar los generadores eléctricos, mientras que el calor a la atmósfera o un cuerpo de agua cercano se utiliza para el papel del disipador de calor. En un motor de combustión interna, se usa una mezcla de gas y aire caliente para empujar un pistón, y el calor se descarga a la atmósfera cercana de una manera similar.
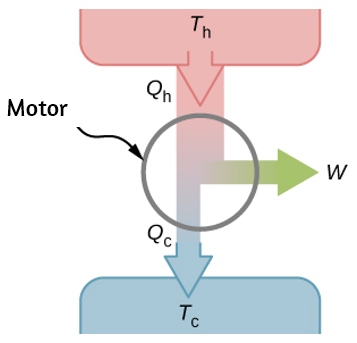
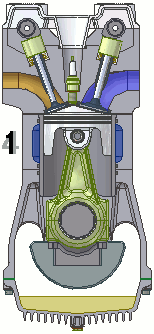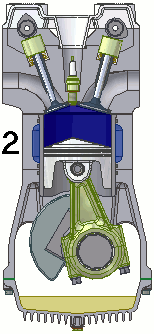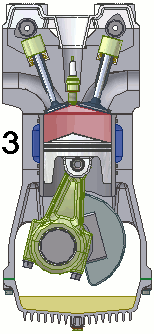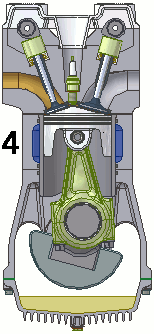
Los motores de calor reales tienen muchos diseños diferentes. Los ejemplos incluyen los motores de combustión interna, como los que se utilizan en la mayoría de los automóviles de hoy en día, y los motores de combustión externa, como las máquinas de vapor utilizadas en los antiguos trenes de vapor. La muestra una foto de una planta de energía nuclear en operación. La atmósfera alrededor de los reactores actúa como el depósito frío, y el calor generado por la reacción nuclear proporciona el calor del depósito caliente.

Las máquinas térmicas funcionan al transportar una sustancia activa durante un ciclo. En una planta de energía de vapor, la sustancia de trabajo es agua, que se inicia como un líquido, se vaporiza, luego se utiliza para impulsar una turbina y finalmente se condensa nuevamente en el estado líquido. Como es el caso de todas las sustancias activas en procesos cíclicos, una vez que el agua vuelve a su estado inicial, repite la misma secuencia.
Por ahora, suponemos que los ciclos de las máquinas térmicas son reversibles, por lo que no hay pérdida de energía por fricción u otros efectos irreversibles.
Supongamos que el motor de la pasa por un ciclo completo y que $Q_h$, $Q_c$ y $W$ representan los calores intercambiados y el trabajo realizado para ese ciclo. Como los estados inicial y final del sistema son iguales, $ΔE_{\textsf{int}} = 0$ para el ciclo. Por lo tanto, tenemos desde la primera ley de la termodinámica,
$$W = Q − ΔE_{\textsf{int}} = (Q_h − Q_c) − 0$$por lo tanto,
La medida más importante de una máquina térmica es su eficiencia $(e),$ que es simplemente "lo que obtenemos" dividido por "lo que ponemos" durante cada ciclo, que se define por $e = W_{\textsf{out}}/Q_{\textsf{in}}$.
Con una máquina térmica trabajando entre dos depósitos de calor, salimos de $W$ y ponemos $Q_h$, por lo que la eficiencia del motor es
Aquí, utilizamos la Ecuación 4.1, $W = Q_h − Q_c$, en el paso final de esta expresión para la eficiencia.
Ejemplo 4.1
Una podadora de césped
Una cortadora de césped tiene una eficiencia del $25.0$% y una potencia promedio de $3.00 kW$. ¿Cuáles son (a) el trabajo promedio y (b) la descarga mínima de calor en el aire por la cortadora de césped en un minuto de uso?
Estrategia
A partir de la potencia promedio, es decir, la tasa de producción de trabajo, podemos deducir el trabajo realizado en el tiempo transcurrido dado. Entonces, a partir de la eficiencia dada, podemos deducir la descarga de calor mínima $Q_c = Q_h(1 - e) con Q_h = Q_c + W$.
Solución
a. El trabajo promedio entregado por el cortacésped es
$$W = PΔt = 3.00 × 10^3 × 60 × 1.00 J = 180 kJ$$b. El calor mínimo descargado en el aire viene dado por
$$Q_c = Q_h(1 - e) = (Q_c + W)(1 - e)$$lo que lleva a
$$Q_c = W(1/e - 1) = 180 × (1/0.25 - 1) kJ = 540 kJ$$Explicación
A medida que aumenta la eficiencia, disminuye el calor mínimo descargado. Esto ayuda a nuestro medio ambiente y la atmósfera al no expulsar tanto calor residual.
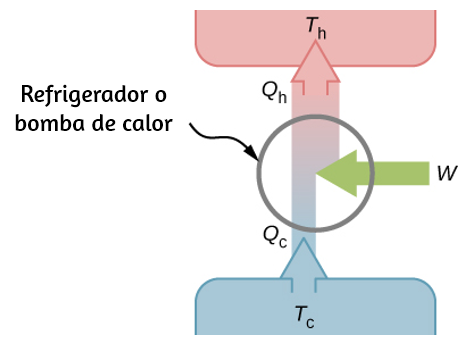
Los ciclos que usamos para describir el motor en la sección anterior son todos reversibles, por lo que cada secuencia de pasos se puede realizar fácilmente en la dirección opuesta. En este caso, el motor se conoce como refrigerador o bomba de calor, dependiendo de cuál sea el foco: el calor extraído del depósito frío o el calor vertido al depósito caliente.
O bien un refrigerador o una bomba de calor es un motor que funciona a la inversa. Para un refrigerador, la atención se centra en eliminar el calor de un área específica. Para una bomba de calor, la atención se centra en descargar calor a un área específica.
Primero consideramos un refrigerador (). El propósito de este motor es eliminar el calor del depósito frío, que es el espacio dentro del refrigerador para un refrigerador doméstico real o el espacio dentro de un edificio para una unidad de aire acondicionado.
Un refrigerador (o bomba de calor) absorbe $Q_c$ de calor del depósito frío a temperatura Kelvin $T_c$ y desecha calor $Q_h$ al depósito caliente a temperatura Kelvin $T_h$, mientras que el trabajo $W$ se realiza en la sustancia activa del motor, como se muestra con la flecha apuntando hacia sistema en la figura. Un refrigerador doméstico elimina el calor de la comida dentro de él y agota el calor del aire circundante. El trabajo requerido, por el cual pagamos en nuestra factura de electricidad, es realizado por el motor que mueve un refrigerante a través de las bobinas. En la se presenta un esquema de un refrigerador doméstico.
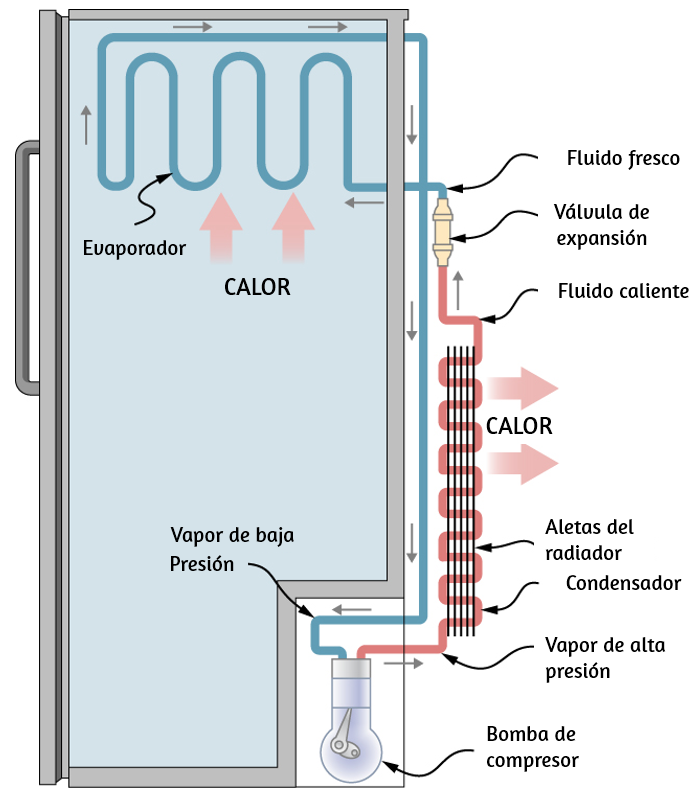
La efectividad o coeficiente de rendimiento $KR$ de un refrigerador se mide por el calor eliminado del depósito frío dividido por el trabajo realizado por la sustancia activa ciclo por ciclo:
Ten en cuenta que hemos utilizado la condición de conservación de energía, $W = Q_h - Q_c$, en el paso final de esta expresión.
La efectividad o el coeficiente de rendimiento $KP$ de una bomba de calor se mide por el calor descargado al depósito caliente dividido por el trabajo realizado en el motor en la sustancia activa ciclo por ciclo:
Una vez más, usamos la condición de conservación de energía $W = Q_h - Q_c$.
Anteriormente, en este capítulo, presentamos la declaración de Clausius de la segunda ley de la termodinámica, que se basa en la irreversibilidad del flujo de calor espontáneo. Como comentamos entonces, la segunda ley de la termodinámica se puede establecer de varias maneras diferentes, y se puede demostrar que todas ellas implican a las otras.
En términos de motores de calor o máquinas térmicas, la segunda ley de la termodinámica se puede establecer de la siguiente manera:
Segunda ley de la Termodinámica (declaración de Kelvin)
Es imposible convertir el calor de una sola fuente en trabajo sin ningún otro efecto.
Esto se conoce como la declaración de Kelvin de la segunda ley de la termodinámica. Esta declaración describe un "motor perfecto" inalcanzable, como se representa esquemáticamente en la (a). Ten en cuenta que "sin ningún otro efecto" es una restricción muy fuerte. Por ejemplo, un motor puede absorber calor y convertirlo todo en trabajo, pero no si completa un ciclo. Sin completar un ciclo, la sustancia en el motor no está en su estado original y, por lo tanto, se ha producido un "otro efecto". Otro ejemplo es una cámara de gas que puede absorber calor de un depósito de calor y funcionar isotérmicamente contra un pistón a medida que se expande. Sin embargo, si el gas regresara a su estado inicial (es decir, hecho para completar un ciclo), tendría que ser comprimido y se tendría que extraer calor de él.
La declaración de Kelvin es una manifestación de un problema de ingeniería bien conocido. A pesar del avance de la tecnología, no podemos construir una máquina térmica que sea 100% eficiente. La primera ley no excluye la posibilidad de construir una máquina perfecta, pero la segunda ley lo prohíbe.
Podemos mostrar que la declaración de Kelvin es equivalente a la declaración de Clausius si vemos los dos objetos en la declaración Clausius como un depósito frío y un depósito caliente.
Por lo tanto, la declaración de Clausius se convierte en: Es imposible construir un refrigerador que transfiera calor de un depósito frío a un depósito caliente sin ayuda de una fuente externa. La afirmación de Clausius se relaciona con la observación cotidiana de que el calor nunca fluye espontáneamente de un objeto frío a un objeto caliente. La transferencia de calor en la dirección de aumento de la temperatura siempre requiere un poco de energía. Un "refrigerador perfecto", que se muestra en la (b), que funciona sin dicha ayuda externa, es imposible de construir.
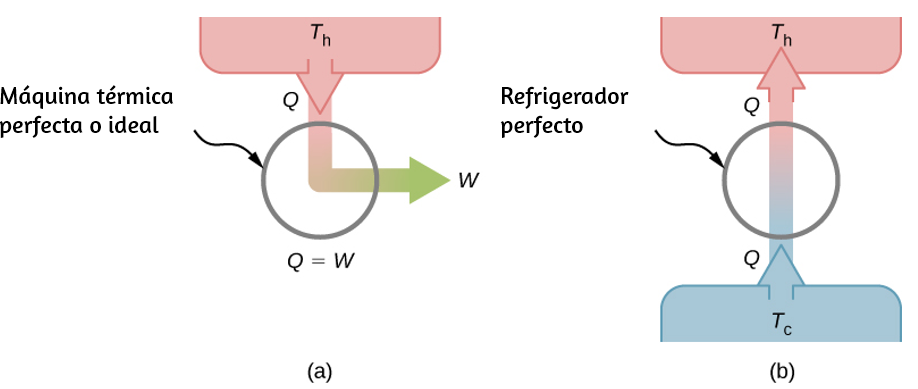
Para demostrar la equivalencia de las declaraciones de Kelvin y Clausius, mostramos que si una afirmación es falsa, se deduce necesariamente que la otra afirmación también es falsa. Supongamos primero que la declaración Clausius es falsa, de modo que existe el refrigerador perfecto de la (b). El refrigerador retira el calor $Q$ de un depósito frío a una temperatura $T_c$ y lo transfiere todo a un depósito caliente a una temperatura $T_h$. Ahora considera un motor térmico real que funcione en el mismo rango de temperatura.
Extrae el calor $Q + ΔQ$ del depósito caliente, trabaja $W$ y descarta el calor $Q$ en el depósito frío. Desde la primera ley, estas cantidades están relacionadas por $W = (Q + ΔQ) - Q = ΔQ$.
Supongamos que estos dos dispositivos se combinan como se muestra en la .
El calor neto eliminado del depósito caliente es $ΔQ$, no se produce transferencia neta de calor hacia o desde el depósito frío, y el trabajo $W$ se realiza en algún cuerpo externo. Dado que $W = ΔQ$, la combinación de un refrigerador perfecto y un motor térmico real es en sí mismo un motor térmico perfecto, lo que contradice la declaración de Kelvin. Por lo tanto, si la declaración de Clausius es falsa, la declaración de Kelvin también debe ser falsa.
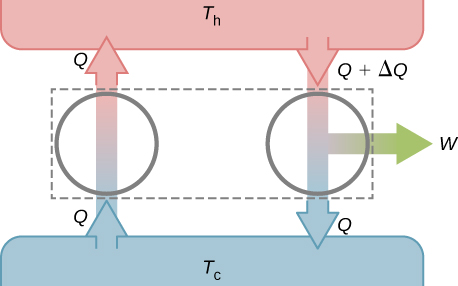
Usando la segunda ley de la termodinámica, ahora demostramos dos propiedades importantes de las máquinas térmicas que funcionan entre dos depósitos de calor. La primera propiedad es que cualquier motor reversible que funcione entre dos depósitos tiene una mayor eficiencia que cualquier motor irreversible que funcione entre los mismos dos depósitos.
La segunda propiedad que debe demostrarse es que todos los motores reversibles que funcionan entre los mismos dos depósitos tienen la misma eficacia.
Para mostrar esto, comenzamos con los dos motores $D$ y $E$ de la (a), que están funcionando entre dos depósitos de calor comunes a temperaturas $T_h$ y $T_c$. Primero, suponemos que $D$ es un motor reversible y que $E$ es un motor hipotético irreversible que tiene una eficiencia mayor que $D$. Si ambos motores realizan la misma cantidad de trabajo $W$ por ciclo, de la Ecuación 4.2 se deduce que $Q_h > Q'_h$. De la primera ley se deduce que $Q_c > Q'_c$.
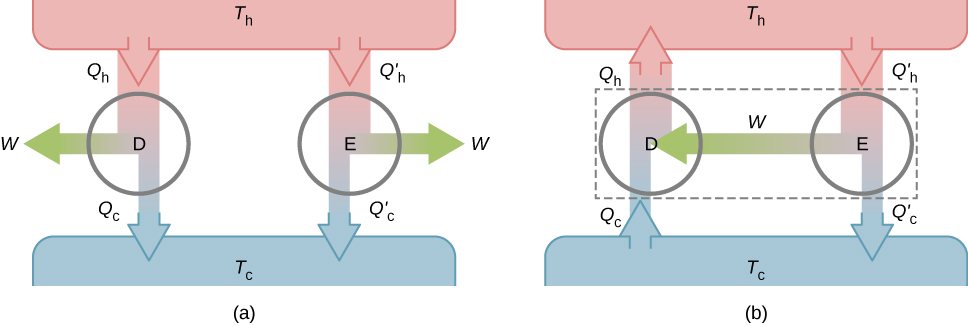
Supongamos que el ciclo de $D$ se invierte para que funcione como un refrigerador, y los dos motores se acoplan de manera que la salida de trabajo de $E$ se utiliza para conducir $D$, como se muestra en la (b).
Desde $Q_h > Q'_h$ y $Q_c > Q'_c$, el resultado neto de cada ciclo es equivalente a una transferencia espontánea de calor del depósito frío al depósito caliente, un proceso que la segunda ley no permite. La suposición original debe, por lo tanto, estar equivocada, y es imposible construir un motor irreversible tal que $E$ sea más eficiente que el motor reversible $D$.
Ahora, es bastante fácil demostrar que las eficiencias de todos los motores reversibles que funcionan entre los mismos depósitos son iguales. Supongamos que $D$ y $E$ son ambos motores reversibles.
Si están acoplados como se muestra en la (b), la eficiencia de $E$ no puede ser mayor que la eficiencia de $D$, o se violaría la segunda ley. Si ambos motores se invierten, el mismo razonamiento implica que la eficiencia de $D$ no puede ser mayor que la eficiencia de $E$. La combinación de estos resultados lleva a la conclusión de que todos los motores reversibles que trabajan entre los mismos dos depósitos tienen la misma eficacia.
 Comprueba tu aprendizaje 4.1
Comprueba tu aprendizaje 4.1
 Comprueba tu aprendizaje 4.2
Comprueba tu aprendizaje 4.2
Conocidas las limitaciones que nos impone la Termodinámica, el ingeniero Carnot diseño un modelo de máquina que las podía satisfacer. En este modelo teórico, no real, ya se ven las características fundamentales de los motores térmicos reales. El sistema se basa en fenómenos de expansión y contracción de gases por ganancia y pérdida de calor. El trabajo de expansión y contracción de los gases puede ser convertido en el movimiento circular típico de la mayoría de las máquinas con facilidad.
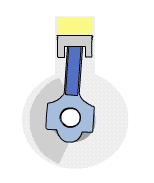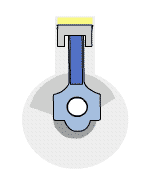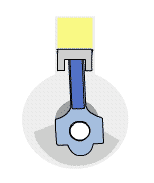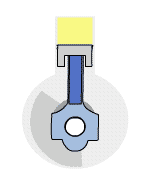
El pistón, mecanismo que vemos en la figura, es el encargado de convertir sus desplazamientos en un movimiento circular, que podremos convertir posteriormente en desplazamiento de un vehículo, movimiento de una grúa, de un robot, etc.
En los motores reales de combustión, la energía se extrae quemando algún combustible, previamente inyectado en el cilindro, finamente pulverizado y mezclado con oxígeno. Después, la mezcla combustible es comprimida y quemada violentamente.
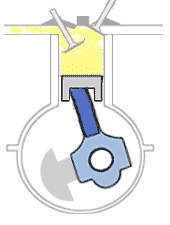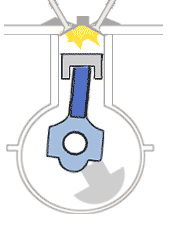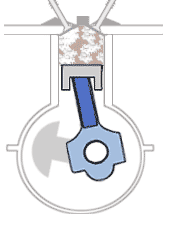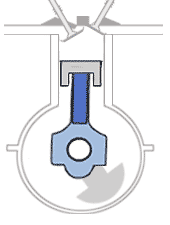
La energía de esta combustión mueve el pistón en varias fases, como se aprecia en la figura.
Esta escena interactiva, diseñada por José Luis San Emeterio Peña, te ayudará a comprender el diseño de Carnot.
En esta escena interactiva, diseñada por José Luis San Emeterio Peña, puedes analizar, de forma aproximada, el ciclo de un motor de combustión moderno.
Fue en 1824 que Sadi Carnot (1786-1832), un ingeniero francés, se interesó en mejorar las eficiencias de los motores térmicos prácticos. Sus estudios lo llevaron a proponer el hipotético ciclo de trabajo con la mayor eficiencia posible entre los mismos dos depósitos o compartimentos, conocido ahora como el ciclo de Carnot. Un motor que opera en este ciclo se llama motor Carnot. El ciclo de Carnot es de especial importancia por una variedad de razones. En un nivel práctico, este ciclo representa un modelo reversible para la planta de energía de vapor y el refrigerador o la bomba de calor. Sin embargo, también es muy importante teóricamente, ya que juega un papel importante en el desarrollo de otra declaración importante de la segunda ley de la termodinámica. Finalmente, debido a que solo dos depósitos están involucrados en su operación, puede usarse junto con la segunda ley de termodinámica para definir una escala de temperatura absoluta que es verdaderamente independiente de cualquier sustancia utilizada para la medición de temperatura.
Con un gas ideal como sustancia de trabajo, los pasos del ciclo de Carnot, como se representa en la , son los siguientes.
1. Expansión isotérmica. El gas se coloca en contacto térmico con un depósito de calor a una temperatura $T_h$. El gas absorbe calor $Q_h$ del depósito de calor y se le permite expandirse isotérmicamente, haciendo el trabajo $W_1$. Debido a que la energía interna $E_{\textsf{int}}$ de un gas ideal es una función de la temperatura solamente, el cambio de la energía interna es cero, es decir, $ΔE_{\textsf{int}} = 0$, durante esta expansión isotérmica. Con la primera ley de la termodinámica, $ΔE_{\textsf{int}} = Q - W$, encontramos que el calor absorbido por el gas es
$$Q_h = W_1 = nRT_hln\frac{V_N}{V_M}$$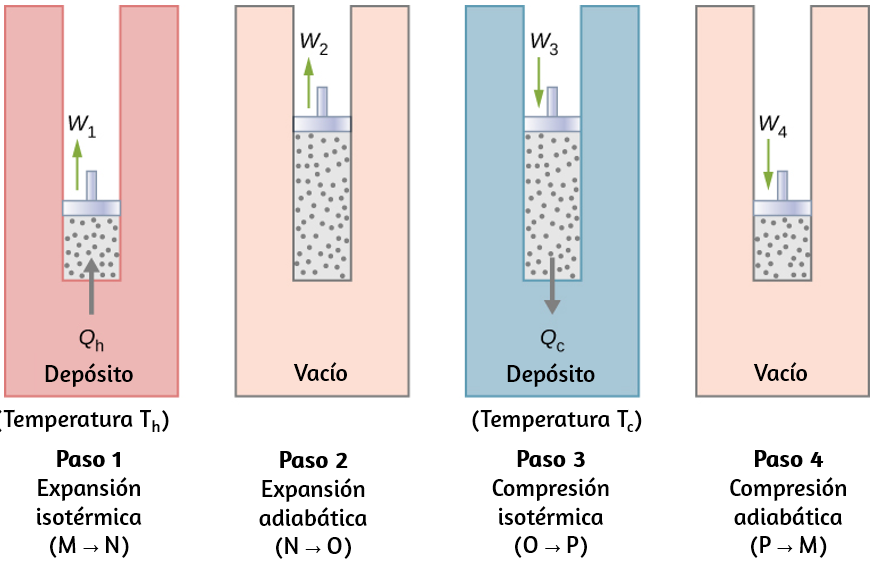
2. Expansión adiabática. El gas está aislado térmicamente y se le permite expandirse aún más, haciendo el trabajo $W_2$. Debido a que esta expansión es adiabática, la temperatura del gas cae, en este caso, desde $T_h$ a $T_c$. De $pVγ = constante$ y la ecuación de estado para un gas ideal, $pV = nRT$, tenemos
$$TV^{γ−1} = constante,$$ $$T_hV_N^{γ−1} = T_cV_O^{γ−1}$$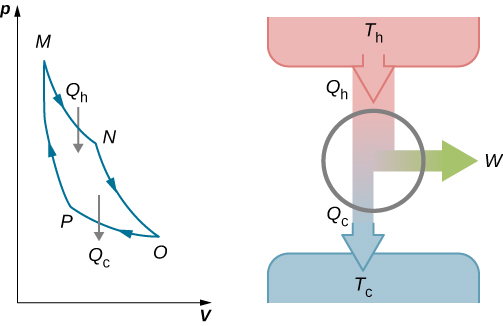
3. Compresión isotérmica. El gas se pone en contacto térmico con un depósito frío a temperatura $T_c$ y se comprime isotérmicamente. Durante este proceso, el trabajo $W_3$ se realiza en el gas y cede calor $Q_h$ al depósito frío. El razonamiento utilizado en el paso 1 ahora produce:
$$Q_c = nRT_cln\frac{V_O}{V_P}$$donde $Q_c$ es el calor arrojado al depósito frío por el gas.
4. Compresión adiabática. El gas se aísla térmicamente y vuelve a su estado inicial por compresión. En este proceso, el trabajo $W_4$ se realiza en el gas. Como la compresión es adiabática, la temperatura del gas aumenta, a partir de $T_c$ a $T_h$ en este caso particular. El razonamiento del paso 2 ahora da
$$T_cV_P^{γ-1} = T_hV_M^{γ-1}$$El trabajo total realizado por el gas en el ciclo de Carnot viene dado por
$$W = W_1 + W_2 - W_3 - W_4$$Este trabajo es igual al área encerrada por el ciclo mostrado en el diagrama $pV$ de la . Debido a que los estados inicial y final del sistema son los mismos, el cambio de la energía interna del gas en el ciclo debe ser cero, es decir, $ΔE_{\textsf{int}} = 0$. La primera ley de la termodinámica nos da
$$W = Q - ΔE_{inr} = (Q_h - Q_c) - 0$$ $$W = Q_h - Q_c$$Para encontrar la eficiencia de este motor, primero dividimos $Q_c$ por $Q_h$:
$$\frac{Q_c}{Q_h} = \frac{T_c}{T_h} \frac{ln(V_O/V_P)}{ln(V_N/V_M)}$$Cuando la constante adiabática del paso 2 se divide por la del paso 4, encontramos
$$\frac{V_O}{V_P} = \frac{V_N}{V_M}$$Sustituyendo esto en la ecuación para $Q_c/Q_h$, obtenemos
$$\frac{Q_c}{Q_h} = \frac{T_c}{T_h}$$Finalmente, con la ecuación 4.2, encontramos que la eficiencia de este motor de Carnot de gas ideal está dada por
Un motor no necesariamente tiene que seguir un ciclo de motor Carnot. Todos los motores, sin embargo, tienen el mismo efecto neto, a saber, la absorción de calor de un depósito caliente, la producción de trabajo y el descarte del calor en un depósito frío. Esto nos lleva a preguntarnos: ¿todos los ciclos reversibles que operan entre los mismos dos depósitos tienen la misma eficacia? La respuesta a esta pregunta proviene de la segunda ley de la termodinámica discutida anteriormente: todos los ciclos reversibles del motor producen exactamente la misma eficiencia. Además, como era de esperar, todos los motores reales que funcionan entre dos depósitos son menos eficientes que los motores reversibles que operan entre los mismos dos depósitos.
Esto también es una consecuencia de la segunda ley de la termodinámica mostrada anteriormente.
El ciclo de un refrigerador Carnot a gas ideal está representado por el diagrama $pV$ de la . Es un motor de Carnot que opera en reversa. El refrigerador extrae el calor $Q_c$ de un depósito de temperatura fría en $T_c$ cuando el gas ideal se expande isotérmicamente.
El gas se comprime adiabáticamente hasta que su temperatura alcanza $T_h$, después de lo cual una compresión isotérmica del gas da como resultado que el calor $Q_h$ se descarte en un depósito de alta temperatura en $T_h$. Finalmente, el ciclo se completa con una expansión adiabática del gas, haciendo que su temperatura baje a $T_c$.
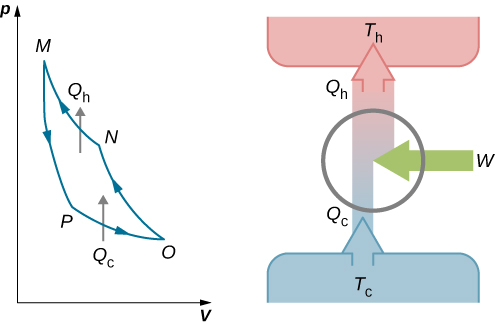
El trabajo realizado en el gas ideal es igual al área delimitada por la ruta del diagrama $pV$. Desde la primera ley, este trabajo es dado por
$$W = Q_h - Q_c$$Un análisis al igual que el análisis realizado para el motor Carnot da
$$Q_cT_c = Q_hT_h$$Cuando se combina con la ecuación 4.3, este rendimiento
para el coeficiente de rendimiento del refrigerador Carnot de gas ideal. Del mismo modo, podemos calcular el coeficiente de rendimiento de una bomba de calor Carnot como
Acabamos de encontrar ecuaciones que representan la eficiencia de un motor Carnot y el coeficiente de rendimiento de un refrigerador Carnot o una bomba de calor Carnot, suponiendo un gas ideal para la sustancia activa en ambos dispositivos.
Sin embargo, estas ecuaciones son más generales de lo que implican sus derivaciones. Pronto demostraremos que ambos son válidos sin importar cuál sea la sustancia activa. Carnot resumió su estudio del motor de Carnot y el ciclo de Carnot en lo que ahora se conoce como el principio de Carnot:
Principio de carnot
Ningún motor que trabaje entre dos depósitos a temperaturas constantes puede tener una mayor eficiencia que un motor reversible.
Este principio se puede ver como otra declaración de la segunda ley de la termodinámica y se puede demostrar que es equivalente a la declaración de Kelvin y la declaración de Clausius.
Ejemplo 4.2
El motor de Carnot
Un motor Carnot tiene una eficiencia de $0.60$ y la temperatura de su depósito frío es de $300 K$. (a) ¿Cuál es la temperatura del depósito caliente? (b) Si el motor hace $300 J$ de trabajo por ciclo, ¿cuánta calor se elimina del depósito de alta temperatura por ciclo? (c) ¿Cuánto calor se agota en el depósito de baja temperatura por ciclo?
Estrategia
De la dependencia de la temperatura de la eficiencia térmica del motor Carnot, podemos encontrar la temperatura del depósito caliente.
Luego, a partir de la definición de la eficiencia, podemos encontrar el calor eliminado cuando se realiza el trabajo realizado por el motor. Finalmente, la conservación de energía conducirá a la cantidad de calor que se debe verter al depósito frío.
Solución
(a) Desde $e = 1 - T_h/T_h$ tenemos $$0.60 = 1 - \frac{300 K}{T_h}$$
para que la temperatura del depósito caliente sea
$$T_h = \frac{300 K}{1 - 0.60} = 750 K$$(b) Por definición, la eficiencia del motor es $e = W/Q$, por lo que el calor eliminado del depósito de alta temperatura por ciclo es
$$Q_h = \frac{W}{e} = \frac{300 J}{0.60} = 500 J$$(c) Desde la primera ley, el calor que el motor descarga al depósito de baja temperatura por ciclo es
$$Q_c = Q_h − W = 500J − 300J = 200J$$Explicación
Un motor Carnot tiene la máxima eficiencia posible de convertir calor en trabajo entre dos depósitos, pero esto no significa necesariamente que sea $100$% eficiente. A medida que aumenta la diferencia en las temperaturas del depósito caliente y frío, aumenta la eficiencia de un motor Carnot.
Ejemplo 4.3
Una bomba de calor de Carnot
Imagina una bomba de calor de Carnot que opera entre una temperatura exterior de $0 °C$ y una temperatura interna de $20.0 °C$. ¿Cuál es el trabajo necesario si el calor suministrado al interior de la casa es de $30.0 kJ$?
Estrategia
Como se supone que la bomba de calor es una bomba de Carnot, su coeficiente de rendimiento viene dado por $K_P = Q_h/W = T_h/(T_h - T_c)$. Por lo tanto, podemos encontrar el trabajo $W$ del calor entregado $Q_h$.
Solución
El trabajo necesario se obtiene de
Explicación
Observamos que este trabajo depende no solo del calor suministrado a la casa sino también de las temperaturas externas e internas. La dependencia de la temperatura exterior hace que no sea práctico su uso en áreas donde la temperatura es mucho más fría que la temperatura ambiente.
En términos de costos de energía, la bomba de calor es un medio muy económico para calentar edificios (). Contrasta este método con convertir la energía eléctrica directamente en calor con elementos de calentamiento resistivos. En este caso, una unidad de energía eléctrica proporciona como máximo solo una unidad de calor. Desafortunadamente, las bombas de calor tienen problemas que limitan su utilidad. Son bastante caras de comprar en comparación con elementos de calefacción resistivos, y, como muestra el coeficiente de rendimiento de una bomba de calor de Carnot, se vuelven menos efectivos a medida que disminuye la temperatura exterior. De hecho, por debajo de aproximadamente $-10 °C$, el calor que suministran es menor que la energía utilizada para operarlos.
 Comprueba tu aprendizaje 4.3
Comprueba tu aprendizaje 4.3

 Comprueba tu aprendizaje 4.4
Comprueba tu aprendizaje 4.4
La segunda ley de la termodinámica se expresa mejor en términos de un cambio en la variable termodinámica conocida como entropía, que se representa con el símbolo $S$. La entropía, como la energía interna, es una función de estado. Esto significa que cuando un sistema hace una transición de un estado a otro, el cambio en la entropía $ΔS$ es independiente de la ruta y depende solo de las variables termodinámicas de los dos estados.
Primero consideramos $ΔS$ para un sistema sometido a un proceso reversible a temperatura constante. En este caso, el cambio en la entropía del sistema está dado por
donde $Q$ es el calor intercambiado por el sistema mantenido a una temperatura $T$ (en kelvin). Si el sistema absorbe calor, es decir, con $Q > 0$, la entropía del sistema aumenta. Como ejemplo, supongamos que un gas se mantiene a una temperatura constante de $300 K$ mientras que absorbe $10 J$ de calor en un proceso reversible. Luego de la Ecuación 4.8, el cambio de entropía del gas es
$$ΔS = \frac{10 J}{300 K} = 0.033 J/K$$Del mismo modo, si el gas pierde $5,0 J$ de calor; es decir, $Q = -5.0 J$, a temperatura $T = 200 K$, tenemos el cambio de entropía del sistema dado por $$ΔS = \frac{-5.0 J}{200 K} = -0.025 J/K$$
Ejemplo 4.4
Entropía. Cambio de fusión del hielo
El calor se agrega lentamente a un trozo de $50 g$ de hielo a $0 °C$ hasta que se derrita por completo en agua a la misma temperatura. ¿Cuál es el cambio de entropía del hielo?
Estrategia
Debido a que el proceso es lento, podemos aproximarlo como un proceso reversible. La temperatura es constante y, por lo tanto, podemos usar la Ecuación 4.8 en el cálculo.
Solución
El hielo se derrite mediante la adición de calor:
$$Q = mL_f = 50g × 335 J/g = 16.8 kJ$$En este proceso reversible, la temperatura de la mezcla de hielo y agua se fija en $0 °C$ o $273 K$. Ahora, desde $ΔS = Q/T$, el cambio de entropía del hielo es $$ΔS = \frac{16.8 kJ}{273 K} = 61.5 J/K$$
cuando se derrite a agua a $0 °C$.
Explicación
Durante un cambio de fase, la temperatura es constante, lo que nos permite usar la Ecuación 4.8 para resolver este problema. La misma ecuación también podría usarse si cambiamos de una fase líquida a una fase gaseosa, ya que la temperatura tampoco cambia durante ese proceso.
El cambio en la entropía de un sistema para una transición arbitraria y reversible para la cual la temperatura no es necesariamente constante se define modificando $ΔS = Q/T$. Imagina un sistema que realiza una transición del estado $A$ al $B$ en pasos pequeños y discretos. Las temperaturas asociadas con estos estados son $T_A$ y $T_B$, respectivamente. Durante cada paso de la transición, el sistema intercambia calor $ΔQ_i$ de forma reversible a una temperatura $T_i$. Esto puede lograrse experimentalmente colocando el sistema en contacto térmico con una gran cantidad de depósitos de calor de diferentes temperaturas $T_i$, como se ilustra en la . El cambio en entropía para cada paso es $ΔS_i = Q_i/T_i$. El cambio neto en la entropía del sistema para la transición es
$$ΔS = S_B − S_A = \sum_i ΔS_i = \sum_i \frac{ΔQ_i}{T_i}$$Ahora tomamos el límite como $ΔQi → 0$, y el número de pasos se acerca al infinito.
Luego, reemplazando la suma por una integral, obtenemos
donde la integral se toma entre el estado inicial $A$ y el estado final $B$. Esta ecuación es válida solo si la transición de $A$ a $B$ es reversible.
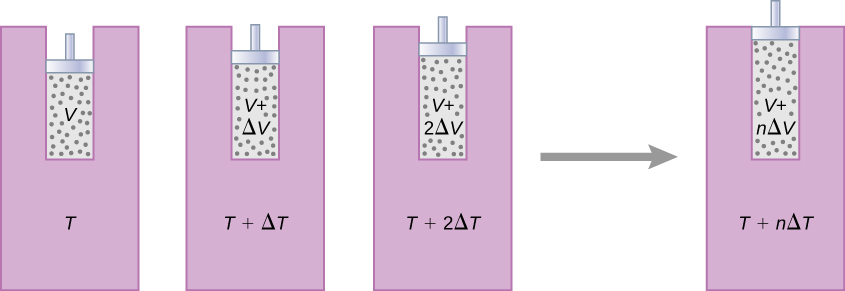
Como ejemplo, determinemos el cambio neto de entropía de un motor reversible mientras se somete a un solo ciclo de Carnot. En los pasos adiabáticos 2 y 4 del ciclo que se muestra en la , no se produce intercambio de calor, entonces $ΔS_2 = ΔS_2 = \int dQ/T = 0$. En el paso 1, el motor absorbe calor $Q_h$ a una temperatura $T_h$, por lo que su cambio de entropía es $ΔS_1 = Q_h/T_h$. De manera similar, en el paso 3, $ΔS_3 = -Q_c/T_c$. El cambio neto de entropía del motor en un ciclo de operación es entonces
$$ΔS_E = ΔS_1 + ΔS_2 + ΔS_3 + ΔS_4 = \frac{Q_h}{T_h} - \frac{Q_c}{T_c}$$Sin embargo, sabemos que para un motor Carnot,
$$\frac{Q_h}{T_h} = \frac{Q_c}{T_c}$$Entonces,
$$ΔS_E = 0$$No hay un cambio neto en la entropía del motor de Carnot en un ciclo completo. Aunque este resultado se obtuvo para un caso particular, se puede demostrar que su validez es mucho más general: no hay un cambio neto en la entropía de un sistema que se somete a cualquier proceso cíclico reversible completo. Matemáticamente, escribimos esta declaración como
donde $\oint$ representa la integral sobre una trayectoria reversible cerrada.
Podemos usar la Ecuación 4.11 para mostrar que el cambio de entropía de un sistema sometido a un proceso reversible entre dos estados dados es independiente de la trayectoria.
En la se muestra un camino cerrado y arbitrario para un ciclo reversible que pasa por los estados $A$ y $B$. De la Ecuación 4.11, $\oint dS = 0$ para esta trayectoria cerrada. Podemos dividir esta integral en dos segmentos, uno a lo largo de $I$, que conduce de $A$ a $B$, el otro a lo largo de $II$, que lleva de $B$ a $A$. Luego
$$\left[\int_A^B ds \right]_I + \left[\int_A^B ds \right]_{II} = 0$$Como el proceso es reversible,
$$\left[\int_A^B ds \right]_I = \left[\int_A^B ds \right]_{II}$$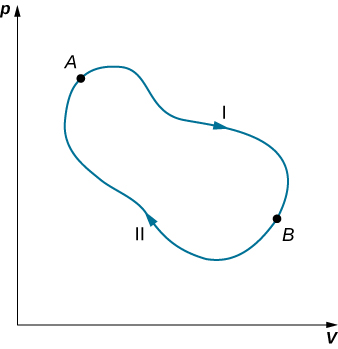
Por lo tanto, el cambio de entropía al pasar de $A$ a $B$ es el mismo para las trayectorias $I$ y $II$. Como las trayectorias $I$ y $II$ son arbitrarias y reversibles, el cambio de entropía en una transición entre dos estados de equilibrio es el mismo para todos los procesos reversibles que unen estos estados. La entropía, al igual que la energía interna, es por lo tanto una función de estado.
¿Qué pasa si el proceso es irreversible? Cuando el proceso es irreversible, esperamos que la entropía de un sistema cerrado, o el sistema y su entorno (el universo), aumenten. Por lo tanto, podemos reescribir esta expresión como
donde S es la entropía total del sistema cerrado o el universo entero, y el signo igual es para un proceso reversible. El hecho es la declaración de entropía de la segunda ley de la termodinámica:
Segunda ley de Termodinámica (declaración de la entropía)
La entropía de un sistema cerrado y el universo entero nunca disminuye.
Podemos demostrar que esta afirmación es consistente con la declaración de Kelvin, la declaración de Clausius y el principio de Carnot.
Ejemplo 4.5
Cambio de entropía de un sistema durante un proceso isobárico
Determina el cambio de entropía de un objeto de masa m y calor específico c que se enfría rápidamente (e irreversiblemente) a presión constante de $T_h$ a $T_c$.
Estrategia
El proceso está claramente establecido como un proceso irreversible; por lo tanto, no podemos simplemente calcular el cambio de entropía del proceso real. Sin embargo, dado que la entropía de un sistema es una función del estado, podemos imaginar un proceso reversible que comience desde el mismo estado inicial y termine en el estado final dado. Entonces, el cambio de entropía del sistema viene dado por la Ecuación 4.10,
$$ΔS = \int_A^B \frac{dQ}{T}$$Solución
Para reemplazar este enfriamiento rápido con un proceso que procede de manera reversible, imaginamos que el objeto caliente se pone en contacto térmico con depósitos de calor sucesivamente más fríos cuyas temperaturas oscilan entre $T_h$ y $T_c$. A lo largo de la transición sustituta, el objeto pierde cantidades infinitesimales de calor $dQ$, por lo que tenemos
$$ΔS = \int_{T_h}^{T_c} \frac{dQ}{T}$$A partir de la definición de capacidad de calor, un intercambio infinitesimal $dQ$ para el objeto está relacionado con su cambio de temperatura $dT$ por
$$dQ = mcdT$$Sustituyendo este $dQ$ en la expresión para $ΔS$, obtenemos el cambio de entropía del objeto a medida que se enfría a presión constante de $T_h$ a $T_c$:
$$ΔS = \int_{T_h}^{T_c} \frac{mcdT}{T} = mcln\frac{T_c}{T_h}$$Ten en cuenta que $ΔS < 0$ aquí porque $T_c < T_h$. En otras palabras, el objeto ha perdido algo de entropía. Pero si contamos todo lo que se usa para eliminar el calor del objeto, aún así terminaríamos con $ΔS_{\textsf{universo}} > 0$ porque el proceso es irreversible.
Explicación
Si la temperatura cambia durante el flujo de calor, debes mantenerlo dentro de la integral para resolver el cambio de entropía. Sin embargo, si la temperatura es constante, simplemente puedes calcular el cambio de entropía como el flujo de calor dividido por la temperatura.
Ejemplo 4.6
Motor Stirling
Los pasos de un motor Stirling reversible son los siguientes. Para este problema, usaremos $0.0010 mol$ de un gas monoatómico que comienza a una temperatura de $133 °C$ y un volumen de $0.10 m^3$, que se llamará punto $A$. Luego sigue los siguientes pasos:
(a) Dibuja el diagrama $pV$ para el motor Stirling con las etiquetas adecuadas.
(b) Completa la siguiente tabla.
| Paso | $W(J)$ | $Q(j)$ | $ΔS (J/K)$ |
| Paso $AB$ | |||
| Paso $BC$ | |||
| Paso $CD$ | |||
| Paso $DA$ | |||
| Ciclo completo |
(c) ¿Cómo se compara la eficiencia del motor Stirling con el motor Carnot que trabaja dentro de los mismos dos depósitos de calor?
Estrategia
Utilizando la ley de los gases ideales, calcula la presión en cada punto para que puedan etiquetarse en el diagrama $pV$. El trabajo isotérmico se calcula usando
$$W = nRTln\frac{V_2}{V_1}$$y un proceso isocórico no se realiza. El flujo de calor se calcula a partir de la primera ley de la termodinámica, $Q = ΔE_{\textsf{int}} - W$ donde $ΔE_{\textsf{int}} = \frac{3}{2}nRΔT$ para gases monoatómicos. Los pasos isotérmicos tienen un cambio en la entropía de $Q/T$, mientras que los pasos isocóricos tienen un $ΔS = \frac{3}{2}nRln\frac{T_2}{T_1}$. La eficiencia de un motor térmico se calcula usando $e_{\textsf{Stir}} = W/Q_h$.
Solución
(a) El gráfico se muestra a continuación.
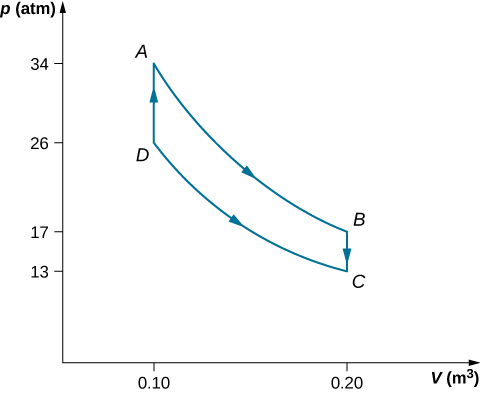
(b) La tabla completa se muestra a continuación.
| Paso | $W(J)$ | $Q(j)$ | $ΔS (J/K)$ |
| Paso $AB$ Isotérmico | $2.3$ | $2.3$ | $0.0057$ |
| Paso $BC$ Isocórico | $0$ | $-1.2$ | $0.0035$ |
| Paso $CD$ Isotérmico | $-1.8$ | $-1.8$ | $-0.0059$ |
| Paso $DA$ Isocórico | $0$ | $1.2$ | $-0.0035$ |
| Ciclo completo | $0.5$ | $0.5$ | $~ 0$ |
(c) La eficiencia del motor térmico Stirling es
$$e_{\textsf{Stir}} = W/Q_h = (Q_{AB} + Q_{CD})/(Q_{AB} + Q_{DA}) = 0.5/4.5 = 0.11$$Si se tratara de un motor de Carnot que opera entre los mismos depósitos de calor, su eficiencia sería
$$e_{\textsf{Car}} = 1 − \frac{T_c}{T_h} = 0.25.$$Por lo tanto, el motor Carnot tendría una mayor eficiencia que el motor Stirling.
Explicación
En los primeros días de las máquinas de vapor, se producían accidentes debido a la alta presión del vapor en la caldera. Robert Stirling desarrolló un motor en 1816 que no usaba vapor y, por lo tanto, era más seguro. El motor Stirling fue utilizado comúnmente en el siglo XIX, pero los desarrollos en los motores de vapor y de combustión interna han dificultado la ampliación del uso del motor Stirling.
El motor Stirling utiliza aire comprimido como sustancia de trabajo, que pasa de una cámara a otra con un tapón poroso, llamado regenerador, que está hecho de un material que no conduce el calor también. En dos de los pasos, los pistones en las dos cámaras se mueven en fase.
A continuación, presentamos una unidad interactiva publicada en la Red Descartes.
Este tipo de unidad interactiva está concebida de tal forma que el alumno descubra por sí mismo las características esenciales de los conceptos estudiados, en nuestro caso la entropía. El diseño del contenido y programación fue realizado por Tine Stalmans (LITE).
Hemos visto cómo la entropía está relacionada con el intercambio de calor a una temperatura particular. En esta sección, consideramos la entropía desde un punto de vista estadístico. Aunque los detalles del argumento están más allá del alcance de este libro de texto, resulta que la entropía puede relacionarse con cuán desordenado o aleatorio es un sistema: cuanto más desordenado, mayor es su entropía. Por ejemplo, una nueva baraja de cartas es muy ordenada, ya que las cartas están dispuestas numéricamente por palo. Al barajar este nuevo mazo, aleatorizamos la disposición de las cartas y, por lo tanto, aumentamos su entropía (). Por lo tanto, al elegir una carta de la parte superior de la baraja, no habría ninguna indicación de cuál será la siguiente carta seleccionada.

La segunda ley de la termodinámica requiere que la entropía del universo aumente en cualquier proceso irreversible. Por lo tanto, en términos de orden, la segunda ley se puede establecer de la siguiente manera:
En cualquier proceso irreversible, el universo se vuelve más desordenado. Por ejemplo, la expansión libre irreversible de un gas ideal, que se muestra en la , da como resultado un mayor volumen para que ocupen las moléculas de gas. Un volumen mayor significa más posible para el mismo número de átomos, por lo que el desorden también se incrementa. Tiene un resultado, la entropía del gas ha subido. El proceso es irreversible. Los cambios en la fase también ilustraron la conexión entre la entropía y el desorden.
Ejemplo 4.7
Entropía. Cambio del Universo
Supongamos que colocamos $50 g$ de hielo a $0 °C$ en contacto con un depósito de calor a $20 °C$. El calor fluye espontáneamente del depósito al hielo, que se funde y alcanza la temperatura de $20 °C$. Encuentra el cambio en la entropía de (a) el hielo y (b) el universo.
Estrategia
Podemos imaginar dos procesos reversibles para el hielo: (1) el hielo se derrite a $0 °C$ ($T_A$); y (2) el hielo derretido (agua) se calienta de $0 °C$ a $20 °C$ ($T_B$) a presión constante. Además del cambio en la entropía del depósito, agregamos al cambio en la entropía del universo.
Solución
a. De la Ecuación 4.10, el aumento en la entropía del hielo es
$$\begin{align*} ΔS_{\textsf{hielo}} &= ΔS_1 + ΔS_2 \\ &= \frac{mL_f}{T_A} + mc \int_A^B \frac{dT}{T} \\ &= \left(\frac{50 × 335}{273} + 50 × 4.19 × ln\frac{293}{273} \right) J/K \\ &= 76.3 J/K \end{align*}$$b. Durante esta transición, el depósito proporciona al hielo una cantidad de calor igual a
$$\begin{align*} Q &= mL_f + mc(T_B − T_A) \\ &= 50 × (335 + 4.19 × 20) J \\ &= 2.10 × 10^4 J \end{align*}$$Esto lleva a un cambio (disminución) en la entropía del depósito:
$$ΔS_{\textsf{depósito}} = \frac{-Q}{T_B} = −71.7 J/K$$El aumento de la entropía del universo es, por lo tanto, $ΔS_{\textsf{universo}} = 76.3 J/K - 71.7 J/K = 4.6 J/K > 0$.
Explicación
La entropía del universo, por lo tanto, es mayor que cero ya que el hielo gana más entropía que el que el reservorio pierde. Si consideramos solo el cambio de fase del hielo en agua y no el aumento de la temperatura, el cambio de entropía del hielo y el depósito sería el mismo, lo que resultaría en que el universo no ganaría entropía.
Este proceso también resulta en un universo más desordenado. El hielo cambia de un sólido con moléculas ubicadas en sitios específicos a un líquido cuyas moléculas son mucho más libres para moverse. Por lo tanto, la disposición molecular se ha vuelto más aleatoria. Aunque el cambio en la energía cinética promedio de las moléculas del depósito de calor es insignificante, no obstante, hay disminución significativa en la entropía del depósito porque tiene muchas más moléculas que el cubo de hielo derretido. Sin embargo, la disminución de la entropía del depósito aún no es tan grande como el aumento de la entropía del hielo. El aumento del desorden del hielo compensa con creces el orden creciente del depósito, y la entropía del universo aumenta en $4.6 J/K$. Puedes sospechar que el crecimiento de las diferentes formas de vida puede ser un proceso de ordenamiento neto y, por tanto, una violación de la segunda ley. Después de todo, una sola célula reúne moléculas y puede convertirse en un organismo altamente estructurado, como un ser humano. Sin embargo, este proceso de ordenamiento está más que compensado por el trastorno del resto del universo. El resultado es un aumento en la entropía y en el desorden del universo.
 Comprueba tu aprendizaje 4.5
Comprueba tu aprendizaje 4.5
La segunda ley de la termodinámica deja en claro que la entropía del universo nunca disminuye durante ningún proceso termodinámico. Para cualquier otro sistema termodinámico, cuando el proceso es reversible, el cambio de la entropía viene dado por $ΔS = Q/T$. Pero, ¿qué sucede si la temperatura va a cero, $T → 0$? Resulta que esta no es una pregunta que pueda ser respondida por la segunda ley. Un problema fundamental sigue siendo: ¿es posible enfriar un sistema hasta cero kelvin? Entendemos que el sistema debe estar en su estado de energía más bajo porque la disminución de la temperatura reduce la energía cinética de los constituyentes en el sistema. ¿Qué le sucede a la entropía de un sistema a la temperatura cero absoluta? Resulta que la temperatura cero absoluta no es alcanzable, al menos, no a través de un número finito de pasos de enfriamiento. Esta es una declaración de la tercera ley de la termodinámica, cuya demostración requiere la mecánica cuántica que no presentamos aquí. En experimentos reales, los físicos han empujado continuamente ese límite hacia abajo, con la temperatura más baja lograda en aproximadamente $1 × 10^{-10} K$ en un laboratorio de baja temperatura en la Universidad de Tecnología de Helsinki en 2008.
Al igual que la segunda ley de la termodinámica, la tercera ley de la termodinámica se puede establecer de diferentes maneras. Una de las declaraciones comunes de la tercera ley de la termodinámica es: La temperatura cero absoluta no se puede alcanzar mediante un número finito de etapas de enfriamiento.
En otras palabras, la temperatura de cualquier sistema físico dado debe ser finita, es decir, $T > 0$. Esto produce una pregunta muy interesante en la física: ¿sabemos cómo se comportaría un sistema si estuviera en la temperatura cero absoluta?
La razón por la que un sistema no puede alcanzar $0 K$ es fundamental y requiere la mecánica cuántica para comprender completamente su origen.
Pero podemos preguntarnos qué le sucede a la entropía de un sistema cuando tratamos de enfriarlo a $0 K$. Debido a que la cantidad de calor que se puede eliminar del sistema es cada vez más pequeña, esperamos que el cambio en la entropía del sistema a lo largo de una isoterma se acerca a cero, es decir,
Esto puede verse como otra declaración de la tercera ley, con todas las isotermas convirtiéndose en isentrópicas, o en una adiabática ideal reversible. Podemos poner esta expresión en palabras: un sistema se vuelve perfectamente ordenado cuando su temperatura se acerca al cero absoluto y su entropía se acerca a su mínimo absoluto.
La tercera ley de la termodinámica pone otro límite a lo que se puedes hacer cuando buscamos recursos energéticos. Si pudiera haber un depósito a la temperatura cero absoluta, podríamos tener motores con una eficiencia del $100$%, lo que, por supuesto, violaría la segunda ley de la termodinámica.
Ejemplo 4.8
Cambio de Entropía de un Gas Ideal en Expansión Libre
Un gas ideal ocupa un volumen dividido $V_1$ dentro de una caja cuyas paredes son térmicamente aislantes, como se muestra en la (a). Cuando se elimina la partición, el gas se expande y llena todo el volumen $V_2$ de la caja, como se muestra en la parte (b). ¿Cuál es el cambio de entropía del universo (el sistema más su entorno)?
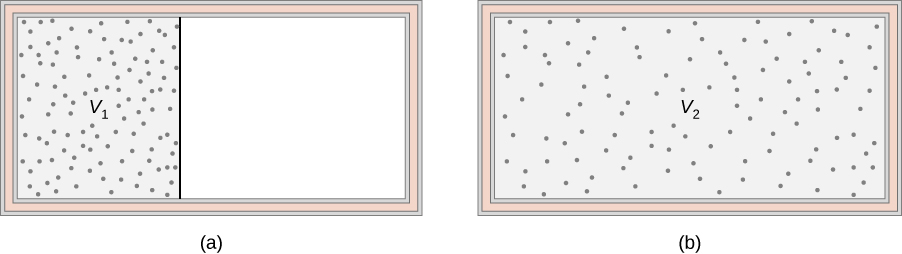
Estrategia
La expansión libre adiabática de un gas ideal es un proceso irreversible. No hay ningún cambio en la energía interna (y por lo tanto, en la temperatura) del gas en dicha expansión porque no ha ocurrido ningún trabajo o transferencia de calor. Por lo tanto, una ruta reversible conveniente que conecta los mismos dos estados de equilibrio es una expansión isotérmica lenta desde $V_1$ a $V_2$. En este proceso, el gas podría expandirse contra un pistón mientras está en contacto térmico con un depósito de calor, como en el paso 1 del ciclo de Carnot.
Solución
Como la temperatura es constante, el cambio de entropía viene dado por $ΔS = Q/T$, donde
$$Q = W = \int _{V_1}^{V_2} pdV$$porque $ΔE_{\textsf{int}} = 0$. Ahora, con la ayuda de la ley de los gases ideales, tenemos
$$Q = nRT\int _{V_1}^{V_2} \frac{dV}{V} = nRTln\frac{V_2}{V_1}$$por lo que el cambio en la entropía del gas es
$$ΔS = \frac{Q}{T} = nRln\frac{V_2}{V_1}$$Porque $V_2 > V_1$, $ΔS$ es positivo, y la entropía del gas ha subido durante la expansión libre.
Explicación
¿Y el medioambiente? Las paredes del contenedor son térmicamente aislantes, por lo que no se produce intercambio de calor entre el gas y su entorno. La entropía del entorno es, por lo tanto, constante durante la expansión.
El cambio neto de entropía del universo es simplemente el cambio de entropía del gas. Como esto es positivo, la entropía del universo aumenta en la expansión libre del gas.
Ejemplo 4.9
Cambio de entropía durante la transferencia de calor
El calor fluye de un objeto de acero de $4.00 kg$ de masa cuya temperatura es de $400 K$ a un objeto idéntico a $300 K$. Suponiendo que los objetos están térmicamente aislados del ambiente, ¿cuál es el cambio de entropía neta del universo después de alcanzar el equilibrio térmico?
Estrategia
Dado que los objetos son idénticos, su temperatura común en equilibrio es de $350 K$. Para calcular los cambios de entropía asociados con sus transiciones, sustituimos el proceso irreversible de la transferencia de calor por dos procesos isobáricos y reversibles, uno para cada uno de los dos objetos. El cambio de entropía para cada objeto viene dado por $ΔS = mcln(T_B/T_A)$.
Solución
Usando $c = 450 J/kg \cdot K$, el calor específico del acero, tenemos para el objeto más caliente
$$ΔS_h = \int _{T_1}^{T_2} \frac{mcdT}{T} = mcln\frac{T_2}{T_1}$$ $$ΔS_h = (4.00 kg)(450 J/kg \cdot K)ln\frac{350 K}{400 K} = −240 J/K$$Del mismo modo, el cambio de entropía del objeto más frío es
$$ΔS_c = (4.00 kg)(450 J/kg \cdot K)ln\frac{350 K}{300 K} = 277 J/K.$$El cambio neto de entropía de los dos objetos durante la transferencia de calor es entonces
$$ΔS_h + ΔS_c = 37 J/K.$$Explicación
Los objetos están térmicamente aislados del entorno, por lo que su entropía debe permanecer constante. Por lo tanto, la entropía del universo también aumenta en $37 J/K$.
 Comprueba tu aprendizaje 4.6
Comprueba tu aprendizaje 4.6
 Comprueba tu aprendizaje 4.7
Comprueba tu aprendizaje 4.7

Cuando estábamos estudiando las leyes de Newton, identificamos varios fenómenos físicos como fuerzas. Lo hicimos en función del efecto que tenían en un objeto físico: específicamente, hacían que el objeto se acelerara. Más tarde, cuando estudiamos el impulso y el momento, ampliamos esta idea para identificar una fuerza como un fenómeno físico que cambia el momento de un objeto. En cualquier caso, el resultado es el mismo: reconocemos una fuerza por el efecto que tiene sobre un objeto.
En Gravitación, examinamos la fuerza de la gravedad, que actúa sobre todos los objetos con masa. En este capítulo, comenzamos el estudio de la fuerza eléctrica, que actúa sobre todos los objetos con una propiedad llamada carga.
La fuerza eléctrica es mucho más fuerte que la gravedad (en la mayoría de los sistemas donde ambos aparecen), pero puede ser una fuerza de atracción o una fuerza de repulsión, lo que produce efectos muy diferentes en los objetos. La fuerza eléctrica ayuda a mantener los átomos juntos, por lo que es de fundamental importancia en la materia. Pero también gobierna la mayoría de las interacciones cotidianas con las que tratamos, desde las interacciones químicas hasta los procesos biológicos.
Seguramente estás familiarizado con los dispositivos electrónicos que activas con el clic de un interruptor, desde computadoras hasta los teléfonos celulares y la televisión. Y ciertamente has visto electricidad en un relámpago durante una fuerte tormenta. Pero también es probable que hayas experimentado efectos eléctricos de otras maneras, tal vez sin darte cuenta de que se trataba de una fuerza eléctrica. Echemos un vistazo a algunas de estas actividades y veamos qué podemos aprender de ellas sobre las cargas y cargas eléctricas.
Probablemente hayas experimentado el fenómeno de la electricidad estática: cuando sacas por primera vez la ropa de una secadora, muchos (no todos) tienden a permanecer juntos; para algunas telas, pueden ser muy difíciles de separar. Otro ejemplo ocurre si te quitas rápidamente un suéter de lana: puedes sentir (y oír) la electricidad estática que tira de tu ropa, y quizás incluso tu cabello.
Si te peinas el cabello en un día seco y luego colocas el peine cerca de una delgada corriente de agua que sale de un grifo, encontrará que la corriente de agua se inclina hacia (se siente atraída por) el peine ().

En la siguiente escena interactiva, diseñada por Julio César Domínguez Tovar, podrás comparar diferentes formas de cargar eléctricamente los objetos, así como detectar la carga a través de la simulación de un electroscopio.
Lo anterior se cumple a través de la manipulación de distintos materiales, como varillas de plástico, vidrio o cobre, que se cargan mediante el frotamiento con otros materiales como piel de conejo, seda, poliéster; teniendo la posibilidad de comparar las cargas eléctricas que se producen.
Supongamos que llevas un peine cerca de unas tiras pequeñas de papel; las tiras de papel son atraídas por el peine e incluso se adhieren a él (). En la cocina, sacas rápidamente un trozo de plástico del rollo; tenderá a adherirse a la mayoría de los materiales no metálicos (como plástico, vidrio o alimentos). Si frotas un globo en la pared por unos segundos, se pegará a la pared. Probablemente el efecto más molesto de la electricidad estática se vea conmocionado por un picaporte (o un amigo) después de arrastrar los pies sobre algunos tipos de alfombras.
Muchos de estos fenómenos se conocen desde hace siglos. El antiguo filósofo griego Tales de Mileto (624-546 aC) registró que cuando el ámbar (una resina dura, translúcida y fosilizada de árboles extintos) se frotaba vigorosamente con un trozo de pelo, se creaba una fuerza que causaba que el pelaje y el ámbar sean atraídos el uno por el otro ().


Además, descubrió que el ámbar frotado no solo atraería el pelaje, y el pelaje atraería al ámbar, sino que ambos podrían afectar a otros objetos (no metálicos), incluso si no están en contacto con esos objetos ().
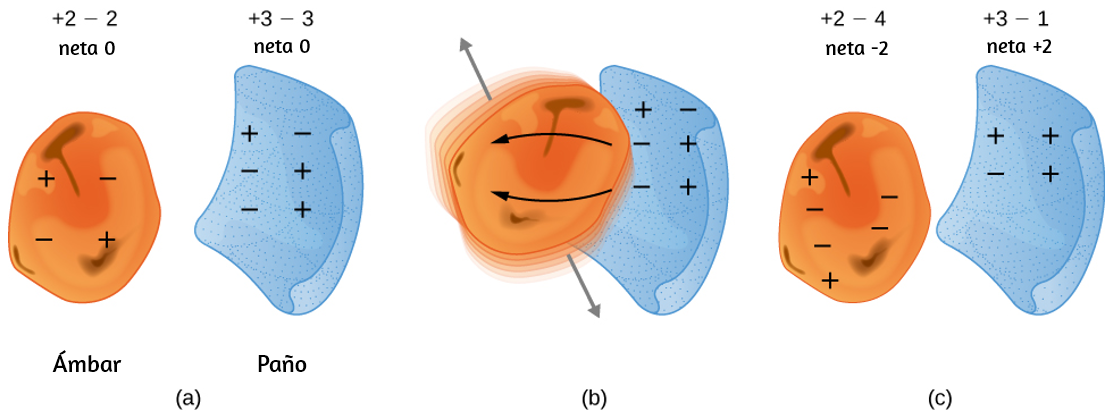
El físico inglés William Gilbert (1544-1603) también estudió esta fuerza atractiva, utilizando varias sustancias. Trabajó con ámbar y, además, experimentó con cristal de roca y varias piedras preciosas y semipreciosas. Él también experimentó con varios metales. Descubrió que los metales nunca exhibieron esta fuerza, mientras que los minerales sí.
Además, aunque una varilla de ámbar electrificada atraería un pedazo de piel, repelería otra varilla ámbar electrificada; de manera similar, dos pedazos de pieles electrificadas se repelerían entre sí.
Esto sugirió que había dos tipos de una propiedad eléctrica, que llegó a llamarse carga eléctrica. La diferencia entre los dos tipos de carga eléctrica está en las direcciones de las fuerzas eléctricas que causa cada tipo de carga. Estas fuerzas son repulsivas cuando existe el mismo tipo de carga en dos objetos que interactúan y son atractivas cuando las cargas son de tipos opuestos.
La unidad SI de carga eléctrica es el culombio ($C$), en honor al físico francés Charles-Augustin de Coulomb (1736-1806). El aspecto más peculiar de esta nueva fuerza es que no requiere contacto físico entre los dos objetos para causar una aceleración. Este es un ejemplo de una fuerza llamada de "largo alcance" (o, como Albert Einstein lo formuló más tarde, "acción a distancia"). Con la excepción de la gravedad, todas las otras fuerzas que hemos discutido hasta ahora actúan solo cuando los dos objetos que interactúan realmente se tocan.
El físico y estadista estadounidense Benjamin Franklin descubrió que podía concentrar la carga en un "frasco de Leyden", que esencialmente era un frasco de vidrio con dos hojas de papel de aluminio, una dentro y otra afuera, con el vidrio entre ellas (). Esto creó una gran fuerza eléctrica entre las dos hojas de aluminio.
Franklin señaló que el comportamiento observado podría explicarse suponiendo que uno de los dos tipos de carga permanecía inmóvil, mientras que el otro tipo de carga fluía de una hoja a otra. Sugirió además que un exceso de lo que él llamó este "fluido eléctrico" se denominará "electricidad positiva" y su deficiencia se denominará "electricidad negativa". Su sugerencia, con algunas modificaciones menores, es el modelo que usamos hoy (Con los experimentos que pudo hacer, esto fue una pura suposición, no tenía forma de determinar realmente el signo de la carga en movimiento. Desafortunadamente, adivinó que no, ahora sabemos que las cargas que fluyen son los que Franklin etiquetó negativas, y las cargas positivas permanecen en gran medida inmóviles. Afortunadamente, como veremos, no establece ninguna diferencia práctica o teórica qué elección hagamos, siempre que nos mantengamos consistentes con nuestra elección).
Hagamos una lista de las observaciones específicas que tenemos de esta fuerza eléctrica:
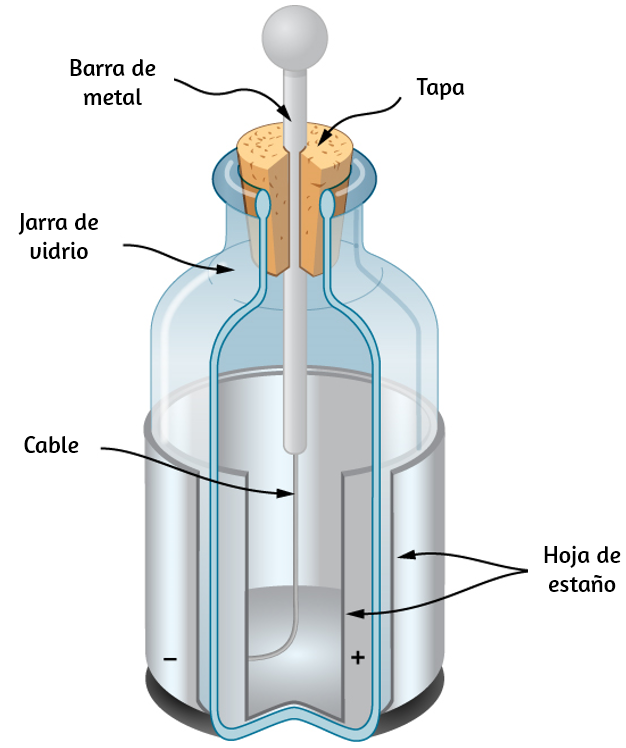
Para ser más precisos, encontramos experimentalmente que la magnitud de la fuerza disminuye a medida que aumenta el cuadrado de la distancia entre los dos objetos que interactúan. Así, por ejemplo, cuando la distancia entre dos objetos que interactúan se duplica, la fuerza entre ellos disminuye a un cuarto de lo que era en el sistema original. También podemos observar que el entorno de los objetos cargados afecta la magnitud de la fuerza. Sin embargo, exploraremos este tema en un capítulo posterior.
Además de la existencia de dos tipos de carga, se han descubierto varias otras propiedades de la carga.
Significa que si dos objetos que tienen cargas iguales y opuestas están físicamente cerca el uno del otro, entonces las fuerzas (opuestamente dirigidas) que se aplican en otro objeto cargado se cancelan, para una fuerza neta cero. Es importante que comprendas que las cargas en los objetos de ninguna manera desaparecen. La carga neta del universo es constante.
Una vez que quedó claro que toda la materia estaba compuesta de partículas que se llamarían átomos, también se hizo evidente rápidamente que los componentes del átomo incluían tanto partículas con carga positiva como partículas con carga negativa. La siguiente pregunta fue, ¿cuáles son las propiedades físicas de esas partículas con carga eléctrica?
La partícula con carga negativa fue la primera en ser descubierta. En 1897, el físico inglés J. J. Thomson estaba estudiando lo que entonces se conocía como rayos catódicos. Algunos años antes, el físico inglés William Crookes había demostrado que estos "rayos" estaban cargados negativamente, pero sus experimentos fueron incapaces de decir nada más que eso (el hecho de que llevaran una carga eléctrica negativa fue una fuerte evidencia de que no eran rayos, sino partículas).
Thomson preparó un haz puro de estas partículas y las envió a través de campos eléctricos y magnéticos cruzados, y ajustó las diversas intensidades de campo hasta que la deflexión neta del rayo fuera cero. Con este experimento, pudo determinar la relación carga-masa de la partícula. Esta relación mostró que la masa de la partícula era mucho más pequeña que la de cualquier otra partícula previamente conocida, de hecho, 1837 veces más pequeña. Eventualmente, esta partícula se llamó el electrón.
Dado que el átomo como un todo es eléctricamente neutro, la siguiente pregunta fue determinar cómo se distribuyen las cargas positivas y negativas dentro del átomo. Thomson mismo imaginó que sus electrones estaban incrustados en una especie de pasta con carga positiva, untada a lo largo del volumen del átomo. Sin embargo, en 1908, el físico neozelandés Ernest Rutherford demostró que las cargas positivas del átomo existían dentro de un núcleo diminuto -llamado núcleo- que ocupaba solo una fracción muy pequeña del volumen total del átomo, pero que contenía más del 99% de la masa. Además, mostró que los electrones con carga negativa orbitaban perpetuamente alrededor de este núcleo, formando una especie de nube cargada eléctricamente que rodea el núcleo (). Rutherford llegó a la conclusión de que el núcleo estaba formado por partículas pequeñas y masivas a las que denominó protones.
Como se sabía que diferentes átomos tienen masas diferentes, y que normalmente los átomos son eléctricamente neutros, era natural suponer que diferentes átomos tienen diferentes números de protones en su núcleo, con un número igual de electrones cargados negativamente que orbitan alrededor del núcleo con carga positiva, haciendo que los átomos sean eléctricamente neutros en general. Sin embargo, pronto se descubrió que aunque el átomo más ligero, el hidrógeno, tenía un solo protón como núcleo, el siguiente átomo más pesado, el helio, tiene el doble de protones (dos), pero cuatro veces la masa de hidrógeno.
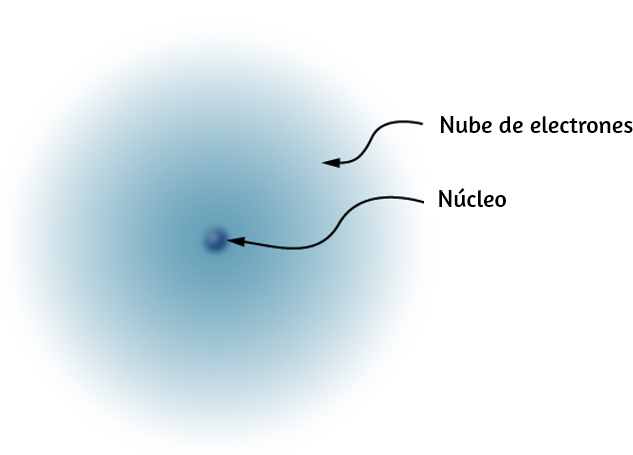
Este misterio fue resuelto en 1932 por el físico inglés James Chadwick, con el descubrimiento del neutrón. El neutrón es, esencialmente, un gemelo eléctricamente neutro del protón, sin carga eléctrica, pero (casi) masa idéntica al protón. El núcleo de helio por lo tanto tiene dos neutrones junto con sus dos protones (los experimentos posteriores mostrarían que aunque el neutrón es eléctricamente neutro en general, sí tiene una estructura de carga interna.
Además, aunque las masas del neutrón y el protón son casi iguales, no son exactamente iguales: la masa del neutrón es ligeramente más grande que la masa del protón. Ese ligero exceso de masa resultó ser de gran importancia. Sin embargo, esa es una historia que deberá esperar hasta nuestro estudio de la física moderna en Física Nuclear).
Así, en 1932, la imagen del átomo era de un núcleo pequeño y masivo construido con una combinación de protones y neutrones, rodeado por una colección de electrones cuyo movimiento combinado formaba una especie de "nube" cargada negativamente alrededor del núcleo ().
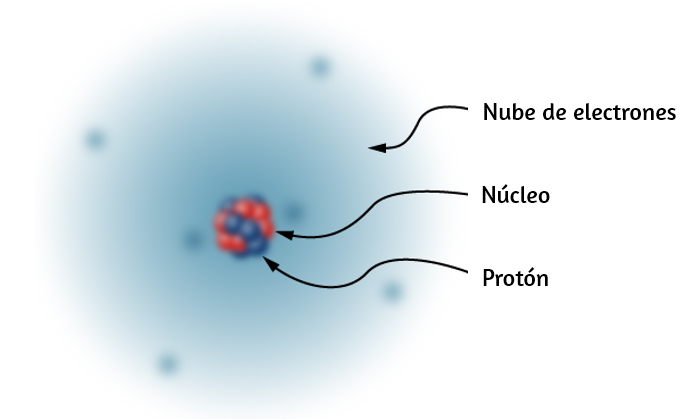
En la siguiente escena interactiva, diseñada por Claudio Francisco Nebbia Rubio, podrás observar estos modelos sobre el átomo. Esta escena hace parte del proyecto Telesecundaria, publicado por la Red Descartes.
En un átomo eléctricamente neutro, la carga negativa total de la colección de electrones es igual a la carga positiva total en el núcleo. Los electrones de muy baja masa pueden eliminarse o agregarse más o menos fácilmente a un átomo, cambiando la carga neta en el átomo (aunque sin cambiar su tipo). Un átomo que ha tenido la carga alterada de esta manera se llama ion. Los iones positivos han eliminado electrones, mientras que los iones negativos tienen exceso de electrones. También usamos este término para describir moléculas que no son eléctricamente neutrales.
Sin embargo, la historia del átomo no se detiene allí. En la última parte del siglo XX, se descubrieron muchas más partículas subatómicas en el núcleo del átomo: piones, neutrinos y quarks, entre otros. Con la excepción del fotón, ninguna de estas partículas es directamente relevante para el estudio del electromagnetismo, por lo que posponemos su discusión hasta el capítulo sobre física de partículas (Física de Partículas y Cosmología).
Como se señaló anteriormente, la carga eléctrica es una propiedad que un objeto puede tener. Esto es similar a cómo un objeto puede tener una propiedad que llamamos masa, una propiedad que llamamos densidad, una propiedad que llamamos temperatura, y así sucesivamente. Técnicamente, siempre deberíamos decir algo así como: "Supongamos que tenemos una partícula que lleva una carga de $3 μC$". Sin embargo, es muy común decir en su lugar: "Supongamos que tenemos una carga de $3 μC$". Del mismo modo, a menudo decimos algo como, "Seis cargas se encuentran en los vértices de un hexágono regular". Una carga no es una partícula; más bien, es una propiedad de una partícula. Sin embargo, esta terminología es extremadamente común (y se usa con frecuencia en este libro, como en cualquier otro lugar). Por lo tanto, ten en mente lo que realmente queremos decir cuando nos referimos a una "carga".
En la sección anterior, dijimos que los científicos podían crear carga eléctrica solo en materiales no metálicos y nunca en metales. Para entender por qué este es el caso, debes comprender más acerca de la naturaleza y la estructura de los átomos. En esta sección, discutimos cómo y por qué las cargas eléctricas se mueven o no a través de los materiales (). Una descripción más completa se da en un capítulo posterior.
Como se discutió en la sección anterior, los electrones rodean el pequeño núcleo en forma de una (comparativamente) gran nube de carga negativa. Sin embargo, esta nube tiene una estructura definida. Consideremos un átomo del conductor más comúnmente utilizado, el cobre.

Por razones que se aclararán en la Estructura Atómica, hay un electrón externo que está solo débilmente ligado al núcleo del átomo. Se puede desalojar fácilmente; luego se mueve a un átomo vecino. En una gran masa de átomos de cobre (como un cable de cobre o una lámina de cobre), estos enormes números de electrones externos (uno por átomo) deambulan de átomo a átomo, y son los electrones que hacen el movimiento cuando fluye la electricidad. Estos electrones errantes o "libres" se llaman electrones de conducción y, por lo tanto, el cobre es un excelente conductor (de carga eléctrica). Todos los elementos conductores tienen una disposición similar de sus electrones, con uno o dos electrones de conducción. Esto incluye la mayoría de los metales.
Los aislantes, por el contrario, están hechos de materiales que carecen de electrones de conducción; la carga fluye solo con gran dificultad, si es que lo hace. Incluso, si se agrega un exceso de carga a un material aislante, no se puede mover, permaneciendo indefinidamente en su lugar. Esta es la razón por la cual los materiales aislantes exhiben las fuerzas de atracción y repulsión eléctricas descritas anteriormente, mientras que los conductores no; cualquier exceso de carga puesta en un conductor se desvanecería instantáneamente (debido a la repulsión mutua de las cargas existentes), sin dejar un exceso de carga para crear fuerzas. La carga no puede fluir a lo largo o a través de un aislante, por lo que sus fuerzas eléctricas permanecen por largos períodos de tiempo (la carga se disipará de un aislante, con tiempo suficiente).
Como sucede, el ámbar, el pelaje y la mayoría de las gemas semipreciosas son aislantes, al igual que los materiales como la madera, el vidrio y el plástico.
Examinemos con más detalle lo que ocurre en un conductor cuando un objeto cargado eléctricamente se acerca a él. Como se mencionó, los electrones de conducción en el conductor pueden moverse con libertad casi total. Como resultado, cuando un aislante cargado (como una varilla de vidrio con carga positiva) se acerca al conductor, la carga (total) en el aislante ejerce una fuerza eléctrica sobre los electrones de conducción. Como la varilla está cargada positivamente, los electrones de conducción (que a su vez están cargados negativamente) son atraídos, fluyendo hacia el aislante hasta el lado más cercano del conductor ().
Ahora, el conductor sigue siendo en general eléctricamente neutral; los electrones de conducción han cambiado de posición, pero todavía están en el material conductor.
Sin embargo, el conductor ahora tiene una distribución de carga; el extremo cercano (la parte del conductor más cercana al aislante) ahora tiene más carga negativa que carga positiva, y la inversa es verdadera para el extremo más alejado del aislante. La reubicación de cargas negativas en el lado más cercano del conductor da como resultado una carga positiva general en la parte del conductor más alejada del aislante. Así hemos creado una distribución de carga eléctrica donde antes no existía. Este proceso se denomina polarización inducida, en este caso, polarizando el conductor. La separación resultante de carga positiva y negativa se denomina polarización, y se dice que un material, o incluso una molécula, que exhibe polarización está polarizado. Una situación similar ocurre con un aislante con carga negativa, pero la polarización resultante es en la dirección opuesta.
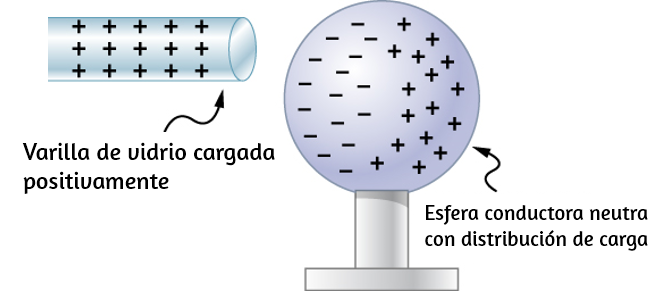
El resultado es la formación de lo que se llama un dipolo eléctrico, de una frase latina que significa "dos extremos". La presencia de cargas eléctricas en el aislante - y las fuerzas eléctricas que se aplican a los electrones de conducción - crea, o "induce" el dipolo en el conductor.
Los objetos neutros pueden ser atraídos por cualquier objeto cargado. Las piezas de paja, por ejemplo, atraídas por el ámbar pulido son neutrales. Si pasas un peine de plástico por el cabello, el peine cargado puede recoger trozos de papel neutros. La muestra cómo la polarización de átomos y moléculas en objetos neutros resulta de su atracción a un objeto cargado.

Cuando una barra cargada se acerca a una sustancia neutra, un aislante en este caso, la distribución de carga en átomos y moléculas se desplaza ligeramente. La carga opuesta es atraída más cerca de la barra cargada externamente, mientras que la carga similar es repelida. Dado que la fuerza electrostática disminuye con la distancia, la repulsión de cargas similares es más débil que la atracción de cargas diferentes, por lo que existe una atracción neta. Por lo tanto, una varilla de vidrio con carga positiva atrae trozos de papel neutros, al igual que una varilla de caucho con carga negativa. Algunas moléculas, como el agua, son moléculas polares. Las moléculas polares tienen una separación de carga natural o inherente, aunque son neutrales en general. Las moléculas polares se ven particularmente afectadas por otros objetos cargados y muestran mayores efectos de polarización que las moléculas con distribuciones de carga naturalmente uniformes.
Cuando se pueden separar los dos extremos de un dipolo, este método de carga por inducción puede usarse para crear objetos cargados sin transferir carga. En la , vemos dos esferas neutras de metal en contacto entre sí, pero aisladas del resto del mundo.
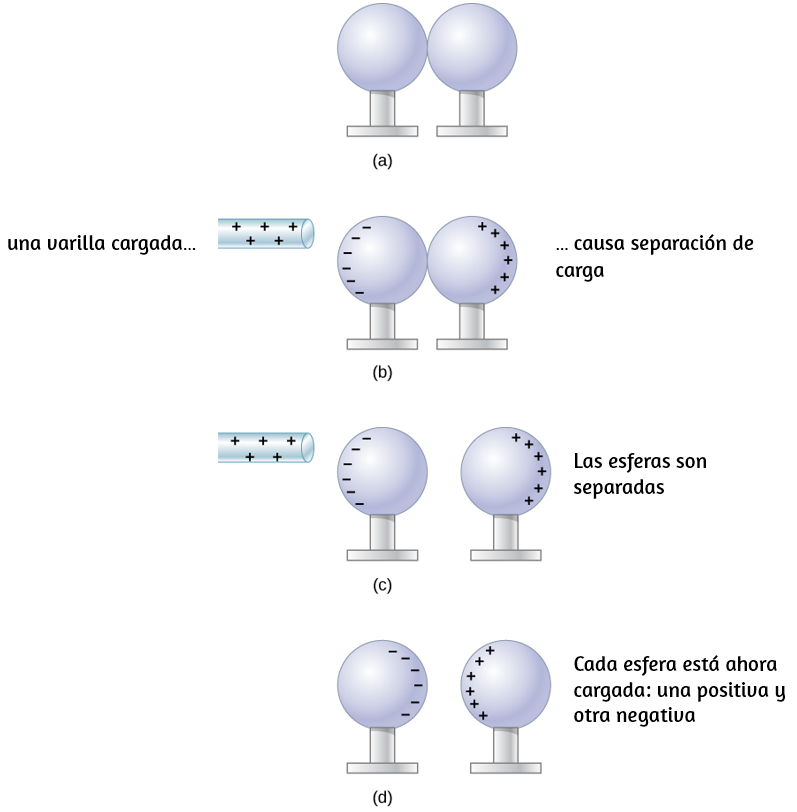
Una barra con carga positiva se acerca a uno de ellos, atrayendo carga negativa hacia ese lado, dejando la otra esfera con carga positiva.
Otro método de carga por inducción se muestra en la . La esfera metálica neutra está polarizada cuando se acerca una barra cargada. La esfera se pone a tierra, lo que significa que un cable conductor se ejecuta desde la esfera hasta el suelo. Como la Tierra es grande y la mayor parte de la tierra es un buen conductor, puede suministrar o aceptar el exceso de carga fácilmente. En este caso, los electrones son atraídos por la esfera a través de un cable llamado cable de tierra, ya que proporciona un camino conductor hacia el suelo.
La conexión a tierra se rompe antes de que se quite la varilla cargada, dejando la esfera con una carga en exceso opuesta a la de la varilla. Nuevamente, se logra una carga opuesta cuando se carga por inducción, y la varilla cargada no pierde nada de su exceso de carga.
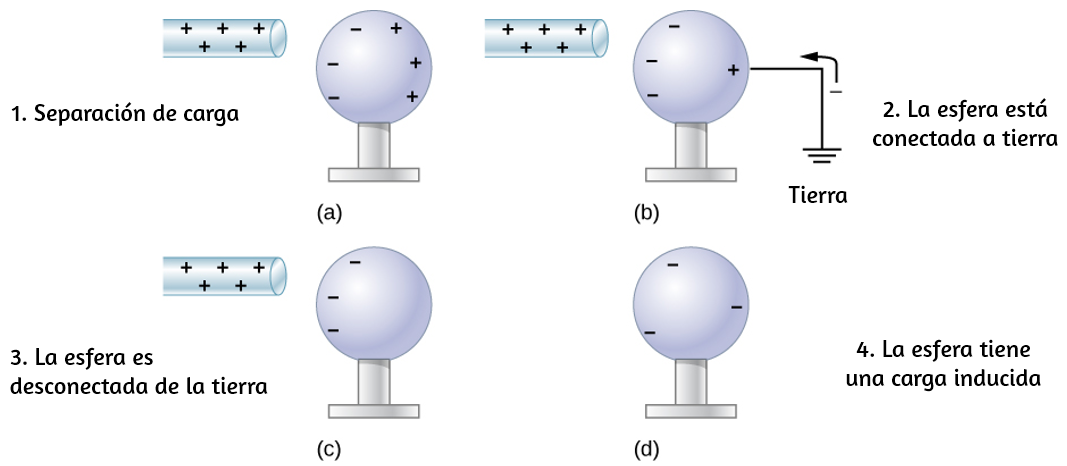
Los experimentos con cargas eléctricas han demostrado que si dos objetos tienen carga eléctrica, ejercen una fuerza eléctrica uno sobre el otro. La magnitud de la fuerza es linealmente proporcional a la carga neta en cada objeto e inversamente proporcional al cuadrado de la distancia entre ellos (curiosamente, la fuerza no depende de la masa de los objetos). La dirección del vector de fuerza se encuentra a lo largo de la línea imaginaria que une los dos objetos y está dictada por los signos de las cargas involucradas.
Sea
La fuerza eléctrica $\overrightarrow{\bold{F}}$ en una de las cargas es proporcional a la magnitud de su propia carga y la magnitud de la otra carga, y es inversamente proporcional al cuadrado de la distancia entre ellos:
$$F ∝ \frac{q_1q_2}{r_{12}^2}$$Esta proporcionalidad se convierte en una igualdad con la introducción de una constante de proporcionalidad. Por razones que se aclararán en un capítulo posterior, la constante de proporcionalidad que usamos es en realidad una colección de constantes.
Ley de Coulomb
La magnitud de la fuerza eléctrica (o fuerza de Coulomb) entre dos partículas cargadas eléctricamente es igual a
$$\overrightarrow{\bold{F}}_{12}(r) = \frac{1}{4π ε_0}\frac{|q_1q_2|}{r_{12}^2} \^{r}_{12} \tag{5.1}$$Usamos signos de valor absoluto alrededor del producto $q_1q_2$, porque una de las cargas puede ser negativa, pero la magnitud de la fuerza siempre es positiva. La dirección del vector de fuerza depende del signo de las cargas. Si las cargas son las mismas, la fuerza apunta lejos una de la otra carga. Si las cargas tienen signos diferentes, la fuerza apunta hacia la otra carga ().

Es importante tener en cuenta que la fuerza eléctrica no es constante, es una función de la distancia de separación entre las dos cargas. Si la carga de prueba o la carga fuente (o ambas) se mueven, entonces $\overrightarrow{\bold{r}}$ cambia, y por lo tanto también lo hace la fuerza. Una consecuencia inmediata de esto es que la aplicación directa de las leyes de Newton con esta fuerza puede ser matemáticamente difícil, dependiendo del problema específico en cuestión.
Por lo general, se puede hacer, pero casi siempre buscamos métodos más fáciles para calcular cualquier cantidad física que nos interese (la conservación de energía es la opción más común).
Finalmente, la nueva constante $ε_0$ en la ley de Coulomb se llama permitividad del espacio libre, o (mejor) la permitividad del vacío.
Tiene un significado físico muy importante que discutiremos en un capítulo posterior; por ahora, es simplemente una constante de proporcionalidad empírica. Su valor numérico (a tres cifras significativas) resulta ser
$$ε_0 = 8.85 × 10^{−12}\frac{C^2}{N \cdot m^2}.$$Se requiere que estas unidades den la fuerza en la ley de Coulomb a las unidades correctas de newtons. Ten en cuenta que en la ley de Coulomb, la permitividad del vacío es solo una parte de la constante de proporcionalidad. Por conveniencia, a menudo definimos una constante de Coulomb:
$$k_e = \frac{1}{4πε_0} = 8.99 × 10^9\frac{N \cdot m^2}{C^2}$$Ejemplo 5.1
La fuerza sobre el electrón en el hidrógeno
Un átomo de hidrógeno consiste en un solo protón y un solo electrón. El protón tiene una carga de $+ e$ y el electrón tiene $-e$. En el "estado fundamental" del átomo, el electrón orbita el protón a la distancia más probable de $5.29 × 10^{-11} m$ (). Calcula la fuerza eléctrica en el electrón debido al protón.
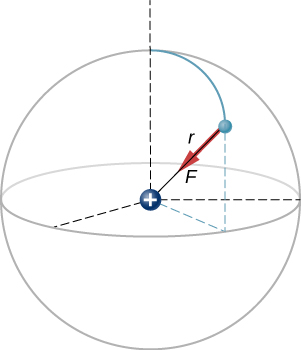
Estrategia
Para los propósitos de este ejemplo, estamos tratando el electrón y el protón como dos partículas puntuales, cada una con una carga eléctrica, y se nos dice la distancia entre ellas; se nos pide que calculemos la fuerza sobre el electrón. Por lo tanto, usamos la ley de Coulomb.
Solución
Nuestras dos cargas y la distancia entre ellas son,
$$\begin{align*} q_1 &= +e = +1.602 × 10^{−19} C \\ q_2 &= -e = -1.602 × 10^{−19} C \\ r &= 5.29 × 10^{−11} m \end{align*}$$La magnitud de la fuerza en el electrón es
$$\begin{align*} F &= \frac{1}{4πε_0}\frac{|e|^2}{^2} \\ &= \frac{1}{4π(8.85 × 10^{−12} C^2/N \cdot m^2)}\frac{(1.602 × 10^{−19} C)^2}{(5.29 × 10^{−11} m)^2} \\ &= 8.25 × 10^{-8} N \end{align*}$$En cuanto a la dirección, dado que las cargas en las dos partículas son opuestas, la fuerza es atractiva; la fuerza en el electrón apunta radialmente y directamente hacia el protón, en todas partes en la órbita del electrón. La fuerza se expresa así
$$\overrightarrow{\bold{F}} = (8.25 × 10^{-8} N) \overrightarrow{\bold{r}}$$Explicación
Este es un sistema tridimensional, por lo que el electrón (y, por lo tanto, la fuerza sobre él) puede estar en cualquier lugar en una capa esférica imaginaria alrededor del protón. En este modelo "clásico" del átomo de hidrógeno, la fuerza electrostática en el electrón apunta en dirección centrípeta hacia adentro, manteniendo así la órbita del electrón. Pero ten en cuenta que el modelo mecánico cuántico del hidrógeno (discutido en Mecánica Cuántica) es completamente diferente.
 Comprueba tu aprendizaje 5.1
Comprueba tu aprendizaje 5.1
La siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, proporciona un entorno para investigar el efecto de una variable sobre otra variable. La cantidad de carga en cada uno de los dos objetos puede cambiarse con los controles tipo barra ubicados en la parte inferior de la escena, y la distancia que los separa pueden cambiarse moviendo las cargas $q_1$ y $q_2$. Cada cuadrado en la cuadrícula de fondo de la escena mide $1.0$ metro. La escena interactivas permite explorar la proporcionalidad directa entre la fuerza y la cantidad de carga en cualquiera de los objetos, y la relación de cuadrados inversos entre la fuerza y la distancia de separación. La distancia de separación se define aquí como la distancia entre los centros de las dos cargas.
Para dar respuesta al "Comprueba tu aprendizaje", cambia los signos de las cargas y observa cómo cambian las fuerzas sobre cada una de las cargas.
La escena interactiva fue diseñada tomando como modelo la presentada en the Physics Classroom, que plantea dos desafíos. El primer desafío consiste en manipular valores de carga para recopilar datos que identifiquen la relación matemática entre la fuerza electrostática y la cantidad de carga en los dos objetos. El segundo desafío implica alterar la distancia de separación para determinar la relación entre la fuerza electrostática y la distancia de separación.
El análisis que hemos hecho para dos partículas se puede extender a un número arbitrario de partículas; simplemente repetimos el análisis, dos cargas a la vez.
Específicamente, hacemos la pregunta: dadas las cargas de $N$ (a los que nos referimos como carga de origen), ¿cuál es la fuerza eléctrica neta que ejercen sobre alguna otra carga puntual (que llamamos la carga de prueba)? Ten en cuenta que usamos estos términos porque podemos pensar en la carga de prueba que se utiliza para probar la fuerza de la fuerza proporcionada por las cargas de origen.
Como todas las fuerzas que hemos visto hasta ahora, la fuerza eléctrica neta en nuestra carga de prueba es simplemente la suma vectorial de cada fuerza eléctrica individual ejercida sobre ella por cada una de las cargas de prueba individuales.
Por lo tanto, podemos calcular la fuerza neta sobre la carga de prueba $Q$ calculando la fuerza sobre ella desde cada carga fuente, tomada una a la vez, y luego sumando todas esas fuerzas juntas (como vectores). Esta capacidad de simplemente sumar fuerzas individuales de esta manera se conoce como el principio de superposición, y es una de las características más importantes de la fuerza eléctrica. En forma matemática, esto se convierte
En esta expresión, $Q$ representa la carga de la partícula que está experimentando la fuerza eléctrica $\overrightarrow{\bold{F}}$, y está ubicada en $\overrightarrow{\bold{r}}$ desde el origen; los $q_i$ son las cargas de fuente $N$, y los vectores $\overrightarrow{\bold{r}}_i = r_i \^{r}_i$ son los desplazamientos desde la posición de la carga iésima a la posición de $Q$. Cada uno de los $N$ vectores de unidades apunta directamente desde su carga fuente asociada hacia la carga de prueba. Todo esto se muestra en la .
Ten en cuenta que no hay diferencia física entre $Q$ y $q_i$; la diferencia en las etiquetas es meramente permitir una discusión clara, siendo $Q$ la carga sobre la que estamos determinando la fuerza.
Ten en cuenta que el vector de fuerza $\overrightarrow{\bold{F}}_i$ no apunta necesariamente en la misma dirección que el vector unitario $r_i$; puede apuntar en la dirección opuesta, $-r_i$. Los signos de la carga fuente y la carga de prueba determinan la dirección de la fuerza en la carga de prueba.
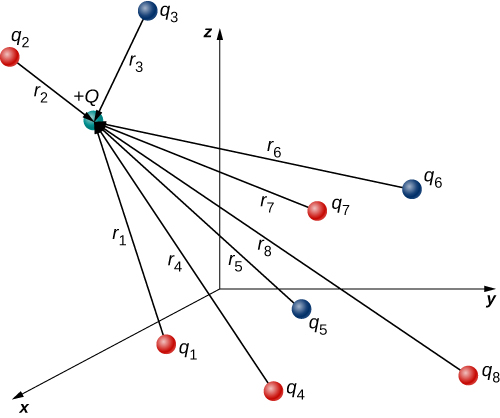
Sin embargo, hay una complicación. Del mismo modo que cada carga fuente ejerce una fuerza sobre la carga de prueba, así también (según la tercera ley de Newton) la carga de prueba ejerce una fuerza igual y opuesta sobre cada una de las cargas fuente. Como consecuencia, cada carga fuente cambiaría de posición. Sin embargo, mediante la Ecuación 5.2, la fuerza en la carga de prueba es una función de la posición; por lo tanto, a medida que cambian las posiciones de las cargas de origen, la fuerza neta en la carga de prueba cambia necesariamente, lo que cambia la fuerza, lo que de nuevo cambia las posiciones. Por lo tanto, todo el análisis matemático se vuelve rápidamente intratable.
Más adelante, aprenderemos técnicas para manejar esta situación, pero por ahora, hacemos la suposición simplificadora de que las cargas de origen se fijan de alguna manera, de modo que sus posiciones sean constantes en el tiempo (la carga de prueba puede moverse.) Con esta restricción en su lugar, el análisis de cargas se conoce como electrostática, donde "estática" se refiere a las posiciones constantes (es decir, estáticas) de las cargas fuente y la fuerza se refiere como una fuerza electrostática.
Ejemplo 5.2
La fuerza neta de dos cargas fuente
Tres diferentes objetos pequeños y cargados se colocan como se muestra en la Figura 5.17. Las cargas $q_1$ y $q_3$ se fijan en su lugar; $q_2$ es libre de moverse. Dado $q_1 = 2e$, $q_2 = -3e$, y $q_3 = -5e$, y que $d = 2.0 × 10^{-7} m$, ¿cuál es la fuerza neta en la carga media $q_2$?
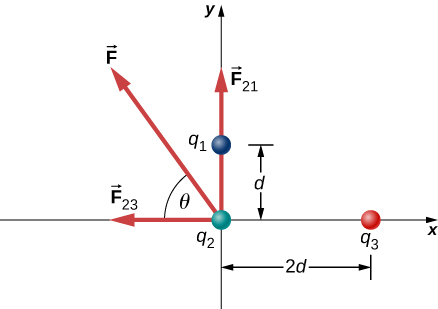
Estrategia
Usamos la ley de Coulomb nuevamente. La forma en que se formula la pregunta indica que $q_2$ es nuestra carga de prueba, por lo que $q_1$ y $q_3$ son cargas fuente.
El principio de superposición dice que la fuerza sobre $q_2$ de cada una de las otras cargas no se ve afectada por la presencia de la otra carga. Por lo tanto, escribimos la fuerza en $q_2$ de cada una y las agregamos juntas como vectores
Solución
Tenemos dos cargas fuente ($q_1$ y $q_3$), una carga de prueba ($q_2$), distancias ($r_{21}$ y $r_{23}$), y se nos pide que encontremos una fuerza. Esto requiere la ley de Coulomb y la superposición de fuerzas. Hay dos fuerzas:
$$\overrightarrow{\bold{F}} = \overrightarrow{\bold{F}}_{21} + \overrightarrow{\bold{F}}_{23} = \frac{1}{4πε_0} \left[\frac{q_2q_1}{r_{21}^2}\^{j} + \left(-\frac{q_2q_3}{r_{23}^2}\^{i} \right) \right]$$No podemos sumar las fuerzas directamente porque no apuntan en la misma dirección: $\overrightarrow{\bold{F}}_{12}$ apunta en la dirección $-x$, mientras que $\overrightarrow{\bold{F}}_{13}$ apunta en la dirección $+ y$. La fuerza neta se obtiene aplicando el teorema de Pitágoras a sus componentes $x$ e $y$.
$$F = \sqrt{F_x^2 + F_y^2}$$donde
$$F_x = -F_{23} = -\frac{1}{4πε_0}\frac{q_2q_3}{r_{23}^2}$$y
$$\begin{align*} F_y &= F_{21} = -\frac{1}{4πε_0}\frac{q_2q_1}{r_{21}^2} \\ F_y &= \left(8.99 × 10^9\frac{N \cdot m^2}{C^2}\right)\frac{(4.806 × 10^{−19} C)(3.204 × 10^{−19} C)}{(2.00 × 10^{−7} m)^2} \\ &= 3.46 × 10^{−14} N \end{align*}$$Encontramos que
$$F = \sqrt{F_x^2 + F_y^2} = 4.08 × 10^{−14} N$$en un ángulo de
$$φ = tan^{−1}\frac{F_y}{F_x} = tan^{−1}\frac{3.46 × 10^{−14} N}{-2.16 × 10^{−14} N} = −58°$$es decir, $58°$ por encima del eje $-x$, como se muestra en el diagrama.
Explicación
Ten en cuenta que cuando sustituimos los valores numéricos de las cargas, no incluimos el signo negativo de $q_2$ o $q_3$. Recuerda que los signos negativos en las cantidades de vectores indican una inversión de la dirección del vector. Pero para las fuerzas eléctricas, la dirección de la fuerza está determinada por los tipos (signos) de ambas cargas que interactúan; determinamos las direcciones de fuerza al considerar si los signos de las dos cargas son iguales o son opuestos.
Si también incluyes signos negativos de cargas negativas cuando sustituyes números, corres el riesgo de invertir matemáticamente la dirección de la fuerza que estás calculando. Por lo tanto, lo más seguro es calcular solo la magnitud de la fuerza, utilizando los valores absolutos de las cargas y determinar las direcciones físicamente.
También vale la pena señalar que el único concepto nuevo en este ejemplo es cómo calcular las fuerzas eléctricas; todo lo demás (obtener la fuerza neta de sus componentes, dividir las fuerzas en sus componentes, encontrar la dirección de la fuerza neta) es lo mismo que los problemas de fuerza que has hecho antes.
 Comprueba tu aprendizaje 5.2
Comprueba tu aprendizaje 5.2
En la siguiente escena interactiva, escrita por Andrew Duffy e inspirada por Jennifer Snyder, puedes explorar la fuerza entre partículas cargadas. Puedes arrastrar las partículas alrededor de la pantalla para cambiar sus posiciones. Si solo quieres dos o tres de ellas, simplemente establece la carga en una o dos de las partículas a cero.
Puedes mostrar (o no) una flecha que representa la fuerza neta que se aplica a cada partícula. También puedes usar las casillas de verificación para mostrar las fuerzas individuales que las otras partículas están aplicando.

Esta escena interactiva de Andrew Duffy es licenciada bajo una Licencia internacional Creative Commons Attribution-ShareAlike 4.0.
La escena se puede encontrar en la colección de http://physics.bu.edu/
Como mostramos en la sección anterior, la fuerza eléctrica neta en una carga de prueba es la suma vectorial de todas las fuerzas eléctricas que actúan sobre ella, de todas las diversas cargas fuente, ubicadas en sus diversas posiciones. Pero, ¿y si usamos una carga de prueba diferente, una con una magnitud diferente, o un signo, o ambos? ¿O supongamos que tenemos una docena de cargas de prueba diferentes que deseamos probar en el mismo lugar? Tendríamos que calcular la suma de las fuerzas desde cero. Afortunadamente, es posible definir una cantidad, llamada campo eléctrico, que es independiente de la carga de prueba. Solo depende de la configuración de las cargas fuente, y una vez encontrada, nos permite calcular la fuerza en cualquier carga de prueba.
Supongamos que tenemos $N$ cargas fuente $q_1, q_2, q_3, ..., q_N$ ubicadas en las posiciones $\overrightarrow{\bold{r}}_1, \overrightarrow{\bold{r}}_2, \overrightarrow{\bold{r}}_3, ..., \overrightarrow{\bold{r}}_N$, aplicando $N$ fuerzas electrostáticas en una carga de prueba $Q$. La fuerza neta en $Q$ es (ver Ecuación 5.2)
$$\begin{align*} \overrightarrow{\bold{F}} &= \overrightarrow{\bold{F}}_1 + \overrightarrow{\bold{F}}_2 + \overrightarrow{\bold{F}}_3 + ... + \overrightarrow{\bold{F}}_N \\ &= \frac{1}{4πϵ_0} \left(\frac{Qq_1}{r_1^2}\^{r}_1 + \frac{Qq_2}{r_2^2}\^{r}_2 + \frac{Qq_3}{r_3^2}\^{r}_3 + ... + \frac{Qq_N}{r_N^2}\^{r}_N \right) \\ &= Q \left[ \frac{1}{4πϵ_0} \left(\frac{q_1}{r_1^2}\^{r}_1 + \frac{q_2}{r_2^2}\^{r}_2 + \frac{q_3}{r_3^2}\^{r}_3 + ... + \frac{q_N}{r_N^2}\^{r}_N \right)\right] \end{align*}$$Podemos reescribir la expresión anterior como
donde
$$\overrightarrow{\bold{E}} = \frac{1}{4πϵ_0} \left(\frac{q_1}{r_1^2}\^{r}_1 + \frac{q_2}{r_2^2}\^{r}_2 + \frac{q_3}{r_3^2}\^{r}_3 + ... + \frac{q_N}{r_N^2}\^{r}_N \right)$$o, más compacto,
Esta expresión se denomina campo eléctrico en la posición $P = P(x, y, z)$ de las cargas de fuente $N$. Aquí, P es la ubicación del punto en el espacio donde se calcula el campo y es relativo a las posiciones $\overrightarrow{\bold{r}}_i$ de las cargas fuente (). Ten en cuenta que tenemos que imponer un sistema de coordenadas para resolver problemas reales.
Ten en cuenta que el cálculo del campo eléctrico no hace referencia a la carga de prueba. Por lo tanto, el enfoque físicamente útil es calcular el campo eléctrico y luego usarlo para calcular la fuerza sobre alguna carga de prueba más tarde, si es necesario. Diferentes cargas de prueba experimentan fuerzas diferentes (Ecuación 5.3), pero es el mismo campo eléctrico (Ecuación 5.4).
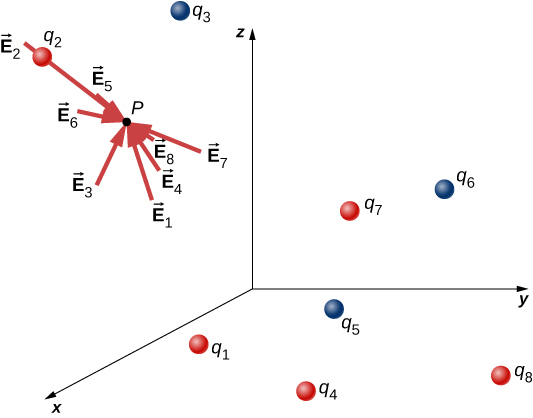
Recuerda que no existe una diferencia fundamental entre una carga de prueba y una carga fuente; estos son simplemente etiquetas convenientes para el sistema de interés. Cualquier carga produce un campo eléctrico; sin embargo, al igual que la órbita de la Tierra no se ve afectada por la propia gravedad de la Tierra, una carga no está sujeta a una fuerza debido al campo eléctrico que genera. Las cargas solo están sujetas a fuerzas provenientes de los campos eléctricos de otras cargas.
A este respecto, el campo eléctrico $\overrightarrow{\bold{E}}$ de una carga puntual es similar al campo gravitacional $\overrightarrow{\bold{g}}$ de la Tierra. Una vez que hayamos calculado el campo gravitacional en algún punto del espacio, podemos usarlo en cualquier momento que queramos calcular la fuerza resultante en cualquier masa que elijamos colocar en ese punto. De hecho, esto es exactamente lo que hacemos cuando decimos que el campo gravitacional de la Tierra (cerca de la superficie de la Tierra) tiene un valor de $9.81 m/s^2$, y luego calculamos la fuerza resultante (es decir, el peso) en diferentes masas. Además, la expresión general para calcular $\overrightarrow{\bold{g}}$ a distancias arbitrarias del centro de la Tierra (es decir, no solo cerca de la superficie de la Tierra) es muy similar a la expresión para $\overrightarrow{\bold{E}}: \overrightarrow{\bold{g}} = \frac{GM}{r^2}\^{r}$, donde $G$ es una constante de proporcionalidad, desempeñando el mismo papel para $\overrightarrow{\bold{g}}$ como $\frac{1}{4πε_0}$ hace para $\overrightarrow{\bold{E}}$. El valor de $\overrightarrow{\bold{g}}$ se calcula una vez y luego se usa en un número infinito de problemas.
Para impulsar aún más la analogía, observa las unidades del campo eléctrico: de $F = QE$, las unidades de $E$ son newtons por culombio, $N/C$, es decir, el campo eléctrico aplica una fuerza en cada unidad de carga. Ahora observa las unidades de $g$: Desde $w = mg$, las unidades de $g$ son newtons por kilogramo, $N/kg$, es decir, el campo gravitacional aplica una fuerza sobre cada unidad de masa. Podríamos decir que el campo gravitatorio de la Tierra, cerca de la superficie de la Tierra, tiene un valor de $9.81 N/kg$.
Recuerda de tus estudios de la gravedad que la palabra "campo" en este contexto tiene un significado preciso.
Un campo, en física, es una cantidad física cuyo valor depende de (es una función de) la posición, relativa a la fuente del campo. En el caso del campo eléctrico, la Ecuación 5.4 muestra que el valor de $\overrightarrow{\bold{E}}$ (tanto la magnitud como la dirección) depende de dónde está ubicado el punto $P$, medido desde las ubicaciones $\overrightarrow{\bold{r}}_i$ de las cargas fuente $q_i$.
Además, dado que el campo eléctrico es una cantidad vectorial, el campo eléctrico se denomina campo vectorial (el campo gravitatorio también es un campo vectorial). En contraste, un campo que tiene solo una magnitud en cada punto es un campo escalar. La temperatura en una habitación es un ejemplo de un campo escalar. Es un campo porque la temperatura, en general, es diferente en diferentes lugares de la sala, y es un campo escalar porque la temperatura es una cantidad escalar.
Además, como lo hiciste con el campo gravitacional de un objeto con masa, debes visualizar el campo eléctrico de un objeto que lleva carga (la carga de la fuente) como una sustancia continua e inmaterial que rodea la carga fuente, llenando todo el espacio en principio, $a ± ∞$ en todas las direcciones. El campo existe en cada punto físico en el espacio. Para decirlo de otra manera, la carga eléctrica en un objeto altera el espacio alrededor del objeto cargado de tal manera que todos los demás objetos cargados eléctricamente en el espacio experimentan una fuerza eléctrica como resultado de estar en ese campo. El campo eléctrico, entonces, es el mecanismo por el cual las propiedades eléctricas de la carga fuente se transmiten a través del resto del universo (de nuevo, el rango de la fuerza eléctrica es infinito).
Sin embargo, otro hecho experimental sobre el campo es que obedece al principio de superposición.
En este contexto, eso significa que podemos (en principio) calcular el campo eléctrico total de muchas cargas fuente calculando el campo eléctrico de solo $q_1$ en la posición $P$, luego calculamos el campo de $q_2$ en $P$. Podemos repetir este proceso, calculando el campo de cada carga fuente individual, independientemente de la existencia de cualquiera de las otras cargas. El campo eléctrico total, entonces, es la suma vectorial de todos estos campos. Eso, en esencia, es lo que dice la Ecuación 5.4.
La ecuación 5.4 nos permite determinar la magnitud del campo eléctrico, pero también necesitamos la dirección. Usamos la convención de que la dirección de cualquier vector de campo eléctrico es la misma que la dirección del vector de fuerza eléctrica que el campo aplicaría a una carga de prueba positiva colocada en ese campo. Tal carga sería repelida por cargas fuente positivas (la fuerza sobre ella apunta lejos de la carga fuente positiva) pero atraída por cargas negativas (la fuerza apunta hacia la fuente negativa).
Dirección del campo eléctrico
Por convención, todos los campos eléctricos $\overrightarrow{\bold{E}}$ apuntan lejos de las cargas fuente positiva y apuntan hacia las cargas fuente negativas.
En la siguiente escena interactiva, diseñada por Andrew Duffy, puedes aumentar el número de cargas fuente, arrastrar las partículas alrededor de la pantalla para cambiar sus posiciones, observar el campo eléctrico y el movimiento de la carga de prueba.
Ejemplo 5.3
El campo $E$ de un átomo
En un átomo de helio ionizado, la distancia más probable entre el núcleo y el electrón es $r = 26.5 × 10^{-12} m$. ¿Cuál es el campo eléctrico debido al núcleo en la ubicación del electrón?
Estrategia
Ten en cuenta que, aunque se menciona el electrón, no se utiliza en ningún cálculo. El problema requiere un campo eléctrico, no una fuerza; por lo tanto, solo hay una carga involucrada, y el problema específicamente pregunta por el campo debido al núcleo. Por lo tanto, el electrón es una cortina de humo, solo su distancia importa. Además, dado que la distancia entre los dos protones en el núcleo es mucho más pequeña que la distancia del electrón del núcleo, podemos tratar los dos protones como una sola carga $+ 2e$ ().
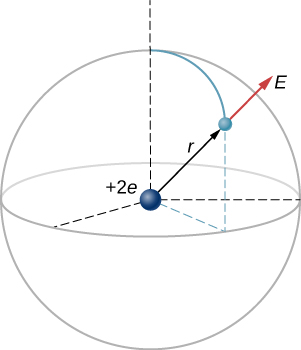
Solución
El campo eléctrico se calcula mediante
$$\overrightarrow{\bold{E}} = \frac{1}{4πε_0}\sum_{i=1}^N \frac{q_i}{r_i^2}\overrightarrow{\bold{r}}_i$$Como solo hay una carga fuente (el núcleo), esta expresión se simplifica a
$$\overrightarrow{\bold{E}} = \frac{1}{4πε_0}\frac{q}{r^2}\overrightarrow{\bold{r}}$$Aquí $q = 2e = 2(1.6 × 10^{-19}C)$ (ya que hay dos protones) y se da $r$; sustituyendo, obtenemos:
$$\begin{align*} \overrightarrow{\bold{E}} &= \frac{1}{4π(8.85 × 10^{−12} C2/N \cdot m^2)}\frac{2(1.6 × 10^{-19} C)}{(26.5 × 10−^{−12} m)^2}\^{r} \\ &= 4.1 × 10^{−12} N/C \^{r} \end{align*}$$La dirección de $\overrightarrow{\bold{E}}$ está radialmente alejada del núcleo en todas las direcciones. ¿Por qué? Debido a que una carga de prueba positiva colocada en este campo se aceleraría radialmente desde el núcleo (ya que también está cargada positivamente), y de nuevo, la convención es que la dirección del vector de campo eléctrico se define en términos de la dirección de la fuerza que se aplicaría a las cargas de prueba positivas.
Ejemplo 5.4
El campo E arriba de dos cargas iguales
(a) Encuentra el campo eléctrico (magnitud y dirección) una distancia $z$ por encima del punto medio entre dos cargas iguales $+ q$ que están separadas por una distancia d (). Verifica que tu resultado sea consistente con lo que esperaría cuando $z >> d$.
(b) Igual que la parte (a), solo que esta vez haz la carga a la derecha $-q$ en lugar de $+ q$.
Estrategia
Agregamos los dos campos como vectores, según la Ecuación 5.4. Observa que el sistema (y por lo tanto el campo) es simétrico respecto al eje vertical; como resultado, las componentes horizontales de los vectores de campo se cancelan. Esto simplifica las matemáticas. Además, nos ocupamos de expresar nuestra respuesta final en términos de solo las cantidades que se dan en la declaración original del problema: $q$, $z$, $d$ y constantes ($π$, $ε_0$).
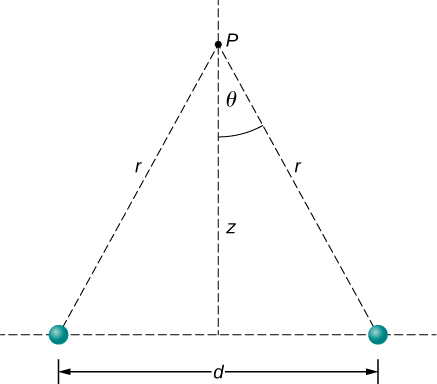
Solución
a. Por simetría, las componentes horizontales ($x$) de $\overrightarrow{\bold{E}}$ se cancelan ();
$$E_x = \frac{1}{4πε_0}\frac{q}{r^2}senθ - \frac{1}{4πε_0}\frac{q}{r^2}senθ = 0$$b. El componente vertical ($z$) viene dado por
$$E_z = \frac{1}{4πε_0}\frac{q}{r^2}cosθ + \frac{1}{4πε_0}\frac{q}{r^2}cosθ = \frac{1}{4πε_0}\frac{2q}{r^2}cosθ$$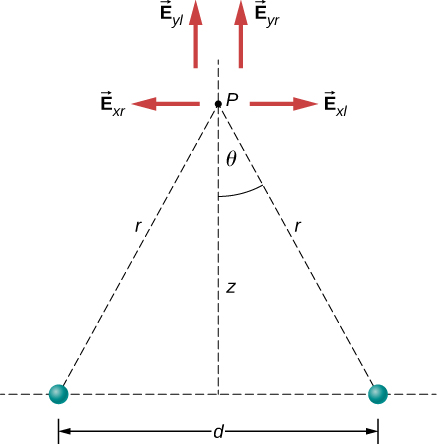
Como ninguno de los otros componentes sobrevive, este es el campo eléctrico completo, y apunta en la dirección $k$. Ten en cuenta que este cálculo utiliza el principio de superposición; calculamos los campos de las dos cargas de forma independiente y luego las agregamos juntas.
Lo que queremos hacer ahora es reemplazar las cantidades en esta expresión que no conocemos (como $r$), o que no podemos medir fácilmente (como $cosθ$) con cantidades que conocemos o que podemos medir. En este caso, por geometría,
y
$$cosθ = \frac{z}{r} = \frac{z}{[z^2 + (d/2)^2]^{1/2}}$$Sustituyendo
$$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0}\frac{2q}{[z^2 + (d/2)^2]}\frac{z}{[z^2 + (d/2)^2]^{1/2}}\^{k}$$Simplificando, la respuesta deseada es
$$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0}\frac{2qz}{[z^2 + (d/2)^2]^{3/2}}\^{k} \tag{5.5}$$b. Si las cargas origen son iguales y opuestas, las componentes verticales se cancelan porque
$$E_z = \frac{1}{4πε_0}\frac{q}{r^2}cosθ - \frac{1}{4πε_0}\frac{q}{r^2}cosθ = 0.$$y obtenemos, para el componente horizontal de $\overrightarrow{\bold{E}}$,
$$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0}\frac{q}{r^2}senθ\^{i} - \frac{1}{4πε_0}\frac{-q}{r^2}senθ\^{i} = \frac{1}{4πε_0}\frac{2q}{r^2}senθ\^{i}$$ $$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0}\frac{2q}{[z^2 + (d/2)^2]}\frac{(d/2)}{[z^2 + (d/2)^2]^{1/2}}$$Esto se convierte en
$$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0}\frac{qd}{[z^2 + (d/2)^2]^{3/2}} \tag{5.6}$$Explicación
Es una técnica muy común y muy útil en física para verificar si tu respuesta es razonable al evaluarla en casos extremos. En este ejemplo, debemos evaluar las expresiones de campo para los casos $d = 0, z >> d$ y $z → ∞$, y confirmar que las expresiones resultantes coinciden con nuestras expectativas físicas. Hagámoslo así:
Comencemos con la Ecuación 5.5, el campo de dos cargas idénticas. Desde muy lejos (es decir, $z >> d$), las dos cargas origen deberían "fusionarse" y deberíamos "ver" el campo de una sola carga, de tamaño $2q$. Por lo tanto, deja $z >> d$; entonces podemos despreciar $d^2$ en la Ecuación 5.5 para obtener
$$\lim{d→0} \overrightarrow{\bold{E}} = \frac{1}{4πε_0}\frac{2qz}{[z^2]^{3/2}}\^{k} = \frac{1}{4πε_0}\frac{2qz}{z^3}\^{k} = \frac{1}{4πε_0}\frac{2q}{z^2}\^{k}$$que es la expresión correcta para un campo a una distancia $z$ de una carga $2q$.
A continuación, consideramos el campo de cargas iguales y opuestas, Ecuación 5.6. Se puede demostrar (a través de una expansión de Taylor) que para $d << z << ∞$, esto se convierte en
$$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0}\frac{qd}{z^3}\^{i} \tag{5.7}$$que es el campo de un dipolo, un sistema que estudiaremos con más detalle más adelante (ten en cuenta que las unidades de $\overrightarrow{\bold{E}}$ siguen siendo correctas en esta expresión, ya que las unidades de $d$ en el numerador cancelan la unidad de $z$ "extra" en el denominador). Si $z$ es muy grande ($z → ∞$), entonces $E → 0$, como debería ser; las dos cargas se "fusionan" y se cancelan.
 Comprueba tu aprendizaje 5.3
Comprueba tu aprendizaje 5.3
Las distribuciones de carga que hemos visto hasta ahora han sido discretas: compuestas de partículas puntuales individuales. Esto está en contraste con una distribución de carga continua, que tiene al menos una dimensión distinta de cero. Si una distribución de carga es continua en lugar de discreta, podemos generalizar la definición del campo eléctrico. Simplemente dividimos la carga en piezas infinitesimales y tratamos cada pieza como una carga puntual.
Ten en cuenta que debido a que la carga se cuantifica, no existe una distribución de carga "verdaderamente" continua. Sin embargo, en la mayoría de los casos prácticos, la carga total que crea el campo involucra una cantidad tan grande de cargas discretas que podemos ignorar de forma segura la naturaleza discreta de la carga y considerarla continua. Este es exactamente el tipo de aproximación que hacemos cuando manejamos un cubo de agua como un fluido continuo, en lugar de una colección de moléculas de $H_2O$. Nuestro primer paso es definir una densidad de carga para una distribución de carga a lo largo de una línea, a través de una superficie o dentro de un volumen, como se muestra en la .
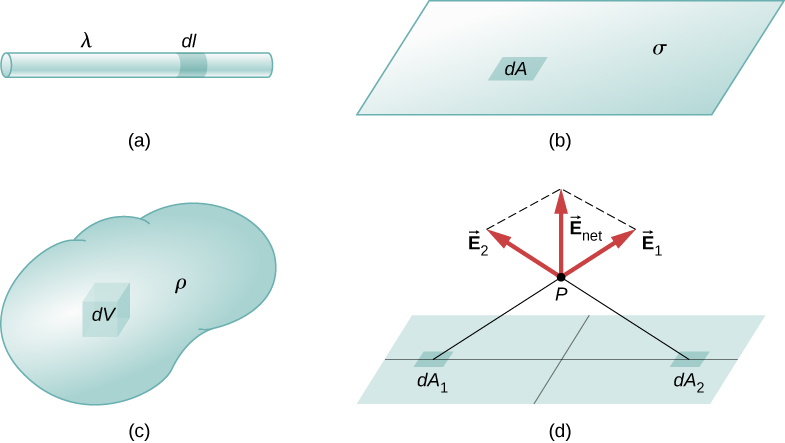
Definiciones de densidad de carga:
Entonces, para una carga lineal, una carga superficial y una carga volumétrica, la suma en la ecuación 5.4 se convierte en una integral y $q_i$ se reemplaza por $dq = λdl$, $σdA$ o $ρdV$, respectivamente:
Las integrales son generalizaciones de la expresión para el campo de una carga puntual. Incluyen implícitamente y asumen el principio de superposición. El "truco" para usarlos casi siempre es encontrar expresiones correctas para $dl$, $dA$ o $dV$, según sea el caso, expresadas en términos de $r$, y también expresar la función de densidad de carga de manera apropiada. Puede ser constante; podría depender de la ubicación.
Observa cuidadosamente el significado de r en estas ecuaciones: es la distancia desde el elemento de carga ($q_i$, $λdl$, $σdA$, $ρdV$) a la ubicación de interés, $P(x, y, z)$ (el punto en el espacio donde desea determinar el campo). Sin embargo, no confundas esto con el sentido de $r$; lo estamos usando con la notación vectorial $\overrightarrow{\bold{E}}$ para escribir tres integrales a la vez. Es decir, la ecuación 5.9 es en realidad
$$\overrightarrow{\bold{E}}_x(P) = \frac{1}{4πε_0} \int_{\textsf{línea}} \left(\frac{λdl}{r^2} \right)_x$$ $$\overrightarrow{\bold{E}}_y(P) = \frac{1}{4πε_0} \int_{\textsf{línea}} \left(\frac{λdl}{r^2} \right)_y$$Ejemplo 5.5
Campo eléctrico de un segmento de línea
Encuentra el campo eléctrico una distancia $z$ por encima del punto medio de un segmento de línea recta de longitud $L$ que lleve una densidad de carga lineal uniforme $λ$.
Estrategia
Como se trata de una distribución de carga continua, separamos el segmento de cable en piezas diferenciales de longitud $dl$
Cada una de estas piezas lleva una cantidad diferencial de carga $dq = λdl$. Luego, calculamos el campo diferencial creado por dos piezas colocadas simétricamente del cable, usando la simetría de la configuración para simplificar el cálculo (.). Finalmente, integramos esta expresión de campo diferencial sobre la longitud del cable (la mitad, en realidad, como explicamos a continuación) para obtener la expresión completa del campo eléctrico.
Solución
Antes de iniciar, ¿cómo esperamos que se vea el campo desde muy lejos? Como es un segmento de línea finita, desde lejos, debe verse como una carga puntual. Comprobaremos la expresión para ver si cumple con esta expectativa.
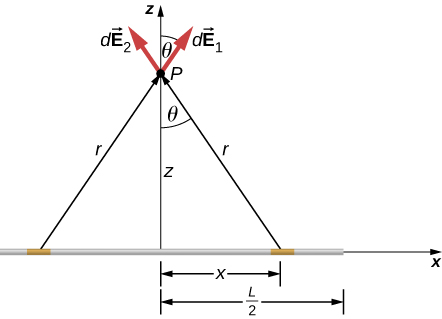
El campo eléctrico para una carga de línea viene dado por la expresión general.
$$\overrightarrow{\bold{E}}(P) = \frac{1}{4πε_0} \int_{\textsf{línea}} \left(\frac{λdl}{r^2} \right)\^{r}$$La simetría de la situación (nuestra elección de las dos piezas de carga diferenciales idénticas) implica cancelar las componentes horizontales ($x$) del campo, de modo que el campo neto apunta en la dirección $z$. Vamos a verificar esto formalmente.
El campo total $\overrightarrow{\bold{E}}(P)$ es la suma vectorial de los campos de cada uno de los dos elementos de carga (llámelos $\overrightarrow{\bold{E}}_1$ y $\overrightarrow{\bold{E}}_1$, por ahora):
Debido a que los dos elementos de carga son idénticos y están a la misma distancia del punto $P$ donde queremos calcular el campo, $E_{1x} = E_{2x}$, entonces esos componentes se cancelan. Esto nos deja
$$\overrightarrow{\bold{E}}(P) = E_{1z}\^{k} + E_{2z}\^{k} = E_1cosθ\^{k} + E_2cosθ\^{k}$$Estos componentes también son iguales, entonces tenemos
$$\begin{align*} \overrightarrow{\bold{E}}(P) &= \frac{1}{4πε_0} \int_{\textsf{línea}}^ (\frac{λdl}{r^2})cosθ\^{k} + \frac{1}{4πε_0} \int_{\textsf{línea}} (\frac{λdl}{r^2})cosθ\^{k} \\ &= \frac{1}{4πε_0} \int_{\textsf{línea}}^ (\frac{2λdl}{r^2})cosθ\^{k} \end{align*}$$donde nuestro elemento de línea diferencial $dl$ es $dx$, en este ejemplo, ya que estamos integrando a lo largo de una línea de carga que se encuentra en el eje $x$ (los límites de integración son $0$ a $L_2$, no $-L_2$ a $+ L_2$, porque hemos construido el campo neto a partir de dos partes diferenciales de carga $dq$. Si integramos a lo largo de toda la longitud, obtendríamos un factor erróneo de 2).
En principio, esto está completo. Sin embargo, para calcular realmente esta integral, necesitamos eliminar todas las variables que no están dadas. En este caso, tanto $r$ como $θ$ cambian a medida que integramos la carga hacia el final de la línea, por lo que esas son las variables de las que debemos deshacernos. Podemos hacer eso de la misma manera que lo hicimos con los dos puntos:
$$r = (z^2 + x^2)^{1/2}$$y
Sustituyendo, obtenemos
$$\begin{align*} \overrightarrow{\bold{E}}(P) &= \frac{1}{4πε_0}\int_0^{L/2} \frac{2λdx}{z^2 + x^2}\frac{z}{(z^2 + x^2)^{1/2}}\^{k} \\ &= \frac{1}{4πε_0}\int_0^{L/2} \frac{2λz}{(z^2 + x^2)^{3/2}}dx\^{k} \\ &= \frac{2λz}{4πε_0}\frac{x}{z^2(z^2 + x^2)^{1/2}}dx\^{k} \end{align*}$$evaluada entre $0$ y $L/2$; que simplificado es
$$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0} \frac{λL}{z\sqrt{z^2 + L^2/4}} \^{k} \tag{5.12}$$Explicación
Observa, una vez más, el uso de la simetría para simplificar el problema. Esta es una estrategia muy común para calcular campos eléctricos. Los campos de distribuciones de carga asimétricas deben manejarse con integrales múltiples y es posible que deba calcularse numéricamente en una computadora.
 Comprueba tu aprendizaje 5.4
Comprueba tu aprendizaje 5.4
Ejemplo 5.6
Campo eléctrico de una línea de carga infinita
Encuentra el campo eléctrico una distancia $z$ por encima del punto medio de una línea de carga infinita que lleva una densidad de carga de línea uniforme $λ$.
Estrategia
Esto es exactamente como en el ejemplo anterior, excepto que los límites de integración serán $-∞$ a $+∞$.
Solución
De nuevo, las componentes horizontales se cancelan, así que terminamos con $$\overrightarrow{\bold{E}}(P) = \frac{1}{4πε_0}\int_{-∞}^∞ \frac{λdx}{r^2}cosθ\^{k}$$
donde nuestro elemento de línea diferencial $dl$ es $dx$, en este ejemplo, ya que estamos integrando a lo largo de una línea de carga que se encuentra en el eje $x$. De nuevo, $$cosθ = \frac{z}{r} = \frac{z}{(z^2 + x^2)^{1/2}}$$
Sustituyendo, obtenemos
$$\begin{align*} \overrightarrow{\bold{E}}(P) &= \frac{1}{4πε_0}\int_{-∞}^{∞} \frac{λdx}{(z^2 + x^2)}\frac{z}{(z^2 + x^2)^{1/2}}\^{k} \\ &= \frac{1}{4πε_0}\int_{-∞}^{∞} \frac{λz}{(z^2 + x^2)^{3/2}}dx\^{k} \\ &= \frac{λz}{4πε_0}[\frac{x}{z^2(z^2 + x^2)^{1/2}}]\^{k} \end{align*}$$evaluada entre $-∞$ e $∞$
Simplificando $$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0}\frac{2λ}{z}\^{k}$$
Explicación
Nuestra estrategia para trabajar con distribuciones de carga continua también brinda resultados útiles para cargas con dimensión infinita.
En el caso de una línea finita de carga, ten en cuenta que para $z >> L$, $z_2$ domina la variable $L$ en el denominador, por lo que la Ecuación 5.12 se simplifica en
$$\overrightarrow{\bold{E}} ≈ \frac{1}{4πε_0}\frac{λL}{z^2}\^{k}$$Si recuerdas que $λL = q$, la carga total en el cable, notarás que hemos recuperado la expresión para el campo de una carga puntual, como se esperaba.
En el límite $L → ∞$, por otro lado, obtenemos el campo de un cable recto infinito, que es un cable recto cuya longitud es mucho, mucho mayor que cualquiera de sus otras dimensiones, y también mucho, mucho mayor que la distancia en el que se calculará el campo:
Una conclusión interesante de este límite infinito es que hemos perdido la dependencia habitual $1/r^2$ a la que estamos acostumbrados. Esto será aún más intrigante en el caso de un plano infinito.
Ejemplo 5.7
Campo eléctrico debido a un anillo de carga
Un anillo tiene una densidad de carga uniforme $λ$, con unidades de culombio por unidad de metro de arco. Encuentra el potencial eléctrico en un punto en el eje que pasa por el centro del anillo.
Estrategia
Usamos el mismo procedimiento que para el cable cargado.
La diferencia aquí es que la carga se distribuye en un círculo. Dividimos el círculo en elementos infinitesimales formados como arcos en el círculo y usamos las coordenadas polares que se muestran en la .
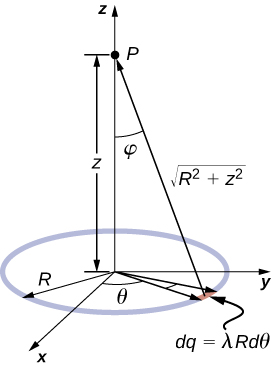
Solución
El campo eléctrico para una carga lineal viene dado por la expresión general
$$\overrightarrow{\bold{E}}(P) = \frac{1}{4πε_0} \int_{\textsf{línea}} \left(\frac{λdl}{r^2} \right)\^{r}$$
En general, un elemento de arco entre $θ$ y $θ + dθ$ es de longitud $Rdθ$ y, por lo tanto, contiene una carga igual a $λRdθ$. El elemento está a una distancia de $r = \sqrt{z^2 + R^2}$ de $P$, el ángulo es $cosφ = \frac{z}{\sqrt{z^2 + R^2}}$, y por lo tanto el campo eléctrico es
$$\begin{align*} \overrightarrow{\bold{E}}(P) &= \frac{1}{4πε_0} \int_{\textsf{línea}} \left(\frac{λdl}{r^2} \right)\^{r} = \frac{1}{4πε_0} \int_0^{2π} \frac{λRdθ}{z^2 + R^2} \frac{z}{\sqrt{z^2 + R^2}} \^{z} \\ &= \frac{1}{4πε_0} \frac{λRz}{(z^2 + R^2)^{3/2}} \^{z} \int_0^{2π} dθ \\ &= \frac{1}{4πε_0} \frac{2πλRz}{(z^2 + R^2)^{3/2}}\^{z} \\ &= \frac{1}{4πε_0}\frac{q_{\textsf{total}}Rz}{(z^2 + R^2)^{3/2}}\^{z} \end{align*}$$Explicación
Como de costumbre, la simetría simplificó este problema, en este caso particular resulta en una integral trivial. Además, cuando tomamos el límite de $z >> R$, encontramos que
$$\overrightarrow{\bold{E}} ≈ \frac{1}{4πε_0}\frac{q_{\textsf{total}}}{z^2}\^{k}$$como esperábamos.
Ejemplo 5.8
El campo de un disco
Encuentra el campo eléctrico de un disco delgado circular de radio $R$ y densidad de carga uniforme a una distancia $z$ por encima del centro del disco ().
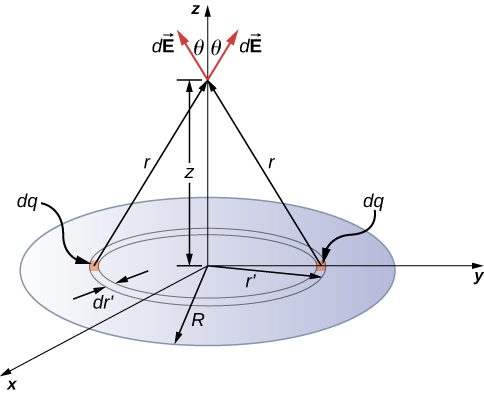
Estrategia
El campo eléctrico para una carga superficial está dado por
$$\overrightarrow{\bold{E}}(P) = \frac{1}{4πε_0} \int_{\textsf{área}} \left(\frac{σdA}{r^2} \right)\^{r}$$Para resolver problemas de carga superficial, dividimos la superficie en "rayas" diferenciales simétricas que coinciden con la forma de la superficie; aquí, usaremos anillos, como se muestra en la figura. De nuevo, por simetría, las componentes horizontales se cancelan y el campo está completamente en la dirección vertical ($k$). El componente vertical del campo eléctrico se extrae multiplicando por cosθ, por lo que
$$\overrightarrow{\bold{E}}(P) = \frac{1}{4πε_0} \int_{\textsf{área}} \left(\frac{σdA}{r^2} \right)cosθ\^{z}$$Como antes, necesitamos reescribir los factores desconocidos en el integrando en términos de las cantidades dadas. En este caso,
$$dA = 2πr'dr$$ $$r^2 = r'^2 + z^2$$ $$cosθ = \frac{z}{(r'^2 + z^2)^{1/2}}$$(Por favor, toma nota de las dos "$r$" diferentes aquí; $r$ es la distancia desde el anillo diferencial de carga al punto $P$ donde queremos determinar el campo, mientras que $r'$ es la distancia desde el centro del disco al anillo diferencial de carga). Además, ya hemos realizado la integral del ángulo polar al escribir $dA$.
Solución
Sustituyendo todo esto, obtenemos
$$\overrightarrow{\bold{E}}(P) = \overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0} \int_0^{R} \frac{σ(2πr'dr')z}{(r'^2 + z^2)^{3/2}}\^{k}$$o, más simple,
$$\overrightarrow{\bold{E}}(z) = \frac{1}{4πε_0} \left(2πσ - \frac{2πσz}{\sqrt{z^2 + R^2}} \right)\^{k} \tag{5.14}$$Explicación
De nuevo, se puede demostrar (mediante una expansión de Taylor) que cuando $z >> R$, esto se reduce a
$$\overrightarrow{\bold{E}}(z) ≈ \frac{1}{4πε_0}\frac{σπR^2}{2}\^{k}$$que es la expresión de una carga puntual $Q = σπR^2$.
 Comprueba tu aprendizaje 5.5
Comprueba tu aprendizaje 5.5
¿Cómo cambiaría el límite anterior con un rectángulo uniformemente cargado en lugar de un disco?
Como $R → ∞$, la Ecuación 5.14 se reduce al campo de un plano infinito, que es una hoja plana cuya área es mucho, mucho mayor que su espesor, y también mucho, mucho mayor que la distancia a la que se calcula el campo:
Ten en cuenta que este campo es constante. Este sorprendente resultado es, una vez más, un artefacto de nuestro límite, aunque uno que utilizaremos repetidamente en el futuro. Para entender por qué sucede esto, imagina que se lo coloca por encima de un plano infinito de carga constante. ¿El plano se ve diferente si varía su altitud? No, aún ves que el plano se va hasta el infinito, sin importar cuán lejos estés de él.
Es importante tener en cuenta que la ecuación 5.15 se debe a que estamos por encima del plano. Si estuviéramos abajo, el campo apuntaría en la dirección $-\^{k}$.
Ejemplo 5.9
El campo de dos planos infinitos
Encuentre el campo eléctrico en todas partes como resultado de dos planos infinitos con densidades de carga iguales pero opuestas ().
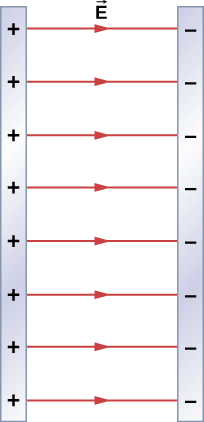
Estrategia
Ya conocemos el campo eléctrico resultante de un único plano infinito, por lo que podemos usar el principio de superposición para encontrar el campo a partir de dos.
Solución
El campo eléctrico apunta desde el plano cargado positivamente hacia el plano cargado negativamente. Dado que los $σ$ son iguales y opuestos, esto significa que en la región fuera de los dos planos, los campos eléctricos se cancelan entre sí.
Sin embargo, en la región entre los planos, los campos eléctricos se suman, y obtenemos
$$\overrightarrow{\bold{E}} = \frac{σ}{ε_0}\^{i}$$para el campo eléctrico. El $\^{i}$ es porque en la figura, el campo apunta en la dirección $+ x$.
Explicación
Los sistemas que pueden aproximarse como dos planos infinitos de este tipo proporcionan un medio útil para crear campos eléctricos uniformes.
 Comprueba tu aprendizaje 5.6
Comprueba tu aprendizaje 5.6
Ahora que tenemos experiencia en el cálculo de campos eléctricos, intentemos obtener una idea de la geometría de los campos eléctricos. Como mencionamos anteriormente, nuestro modelo es que la carga en un objeto (la carga de la fuente) altera el espacio en la región que lo rodea de forma que cuando se coloca otro objeto cargado (la carga de prueba) en esa región del espacio, esa carga de prueba experimenta una fuerza eléctrica. El concepto de líneas de campo eléctrico y de diagramas de líneas de campo eléctrico nos permite visualizar la forma en que se altera el espacio, lo que nos permite visualizar el campo. El propósito de esta sección es permitirte crear bocetos de esta geometría, por lo que enumeraremos los pasos y reglas específicos involucrados en la creación de un boceto preciso y útil de un campo eléctrico.
Es importante recordar que los campos eléctricos son tridimensionales. Aunque en este libro incluimos algunas imágenes pseudo tridimensionales, varios de los diagramas que verás (tanto aquí como en capítulos posteriores) serán proyecciones bidimensionales o secciones transversales. Siempre ten en cuenta que, de hecho, estás viendo un fenómeno tridimensional.
Nuestro punto de partida es el hecho físico de que el campo eléctrico de la carga fuente provoca una carga de prueba en ese campo para experimentar una fuerza.
Por definición, los vectores del campo eléctrico apuntan en la misma dirección que la fuerza eléctrica que experimentaría una carga de prueba positiva (hipotética), si se coloca en el campo ().
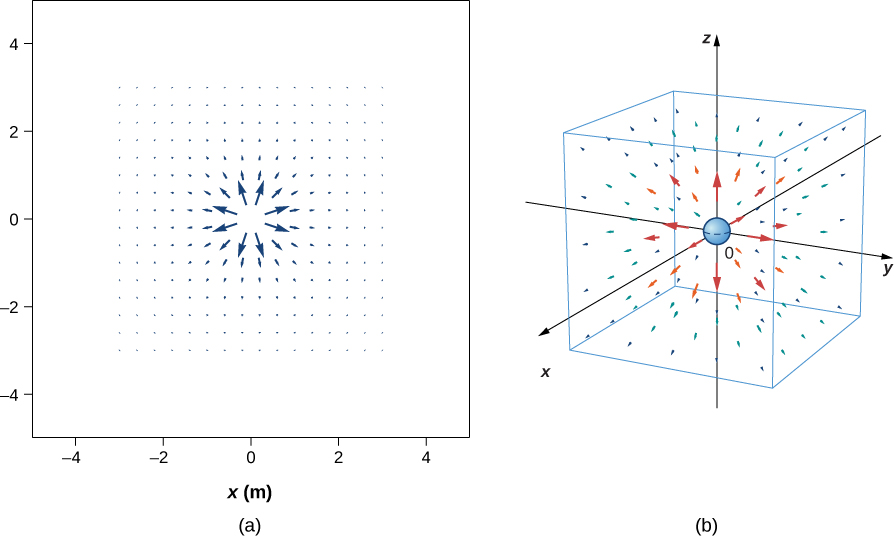
En la siguiente escena interactiva, diseñada por Wolfgang Christian y Anne J Cox, puedes agregar cargas positivas (roja) y negativas (azul), así como cargas de "prueba" (negra).
La carga de prueba es como una carga fantasma: te muestra la fuerza que sentiría una carga positiva en una ubicación determinada, pero no cambia el campo circundante. En otras palabras, la carga de prueba muestra la dirección y la magnitud del campo eléctrico en un punto determinado.
Realiza las siguientes actividades en la escena interactiva.
Hemos trazado muchos vectores de campo en la figura, que se distribuyen uniformemente alrededor de la carga fuente. Como el campo eléctrico es un vector, las flechas que dibujamos corresponden en cada punto del espacio a la magnitud y a la dirección del campo en ese punto. Como siempre, la longitud de la flecha que dibujamos corresponde a la magnitud del vector de campo en ese punto. Para una carga de fuente puntual, la longitud disminuye por el cuadrado de la distancia desde la carga fuente. Además, la dirección del vector de campo está radialmente alejada de la carga fuente, porque la dirección del campo eléctrico se define por la dirección de la fuerza que experimentaría una carga de prueba positiva en ese campo (Nuevamente, ten en cuenta que el campo real es tridimensional, también hay líneas de campo que apuntan hacia y desde la página de este libro).
Este diagrama es correcto, pero se vuelve menos útil a medida que la distribución de la carga fuente se vuelve más complicada. Por ejemplo, considera el diagrama de campo vectorial de un dipolo ().
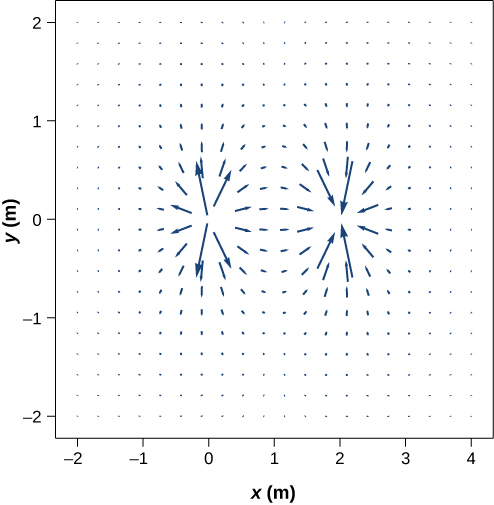
Hay una forma más útil de presentar la misma información. En lugar de dibujar un gran número de flechas vectoriales cada vez más pequeñas, las conectamos todas juntas, formando líneas y curvas continuas, como se muestra en la .
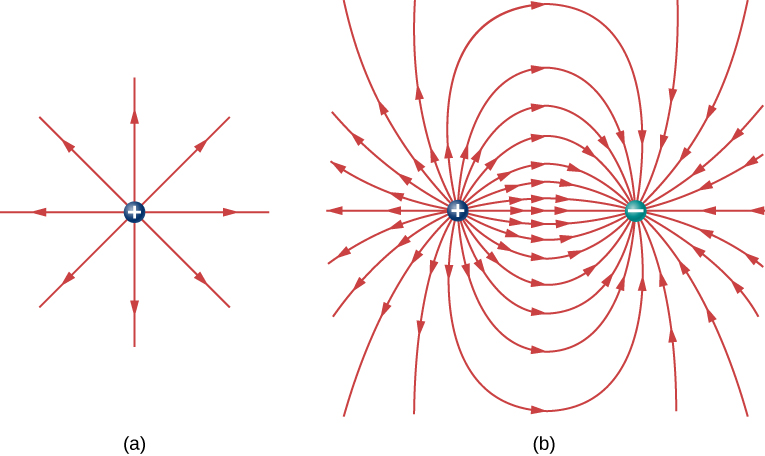
Aunque puede no ser obvio a primera vista, estos diagramas de campo transmiten la misma información sobre el campo eléctrico que los diagramas de vectores. Primero, la dirección del campo en cada punto es simplemente la dirección del vector de campo en ese mismo punto. En otras palabras, en cualquier punto del espacio, el vector de campo en cada punto es tangente a la línea de campo en ese mismo punto. La punta de flecha colocada en una línea de campo indica su dirección. En cuanto a la magnitud del campo, eso se indica por la densidad de la línea de campo, es decir, el número de líneas de campo por unidad de área que pasa a través de un área de sección transversal pequeña perpendicular al campo eléctrico.
Esta densidad de línea de campo se dibuja para que sea proporcional a la magnitud del campo en esa sección transversal. Como resultado, si las líneas de campo están muy juntas (es decir, la densidad de la línea de campo es mayor), esto indica que la magnitud del campo es grande en ese punto. Si las líneas de campo están muy separadas en la sección transversal, esto indica que la magnitud del campo es pequeña. La muestra la idea.
En la , el mismo número de líneas de campo pasa a través de ambas superficies ($S$ y $S'$), pero la superficie $S$ es más grande que la superficie $S'$. Por lo tanto, la densidad de las líneas de campo (número de líneas por unidad de área) es mayor en la ubicación de $S',$ lo que indica que el campo eléctrico es más fuerte en la ubicación de $S'$ que en $S$. Las reglas para crear un diagrama de campo eléctrico son como sigue.
Estrategia para resolver problemas: dibujar líneas de campo eléctrico
1. Las líneas del campo eléctrico se originan en cargas positivas o entran desde el infinito, y terminan en cargas negativas o se extienden hasta el infinito.
2. El número de líneas de campo que se originan o terminan a una carga es proporcional a la magnitud de esa carga. Una carga $2q$ tendrá el doble de líneas que una carga q.
3. En cada punto del espacio, el vector de campo en ese punto es tangente a la línea de campo en ese mismo punto.
4. La densidad de la línea de campo en cualquier punto del espacio es proporcional a (y por lo tanto es representativa de) la magnitud del campo en ese punto del espacio.
5. Las líneas de campo nunca se pueden cruzar. Como una línea de campo representa la dirección del campo en un punto dado, si dos líneas de campo se cruzan en algún punto, eso implicaría que el campo eléctrico apuntaba en dos direcciones diferentes en un solo punto. Esto, a su vez, sugeriría que la fuerza (neta) en una carga de prueba colocada en ese punto apuntaría en dos direcciones diferentes. Como esto es obviamente imposible, se deduce que las líneas de campo nunca deben cruzarse.
Siempre ten en cuenta que las líneas de campo sirven solo como una forma conveniente de visualizar el campo eléctrico; no son entidades físicas. Aunque la dirección y la intensidad relativa del campo eléctrico se pueden deducir a partir de un conjunto de líneas de campo, las líneas también pueden ser engañosas. Por ejemplo, las líneas de campo dibujadas para representar el campo eléctrico en una región deben, por necesidad, ser discretas. Sin embargo, el campo eléctrico real en esa región existe en cada punto del espacio.
Las líneas de campo para tres grupos de cargas discretas se muestran en la . Como las cargas en las partes (a) y (b) tienen la misma magnitud, se muestra el mismo número de líneas de campo comenzando o terminando en cada carga. En (c), sin embargo, dibujamos tres veces más líneas de campo dejando la carga $+ 3q$ entrando a $-q$. Las líneas de campo que no terminan en $-q$ emanan hacia afuera desde la configuración de carga, hasta el infinito.
La capacidad de construir un diagrama de campo eléctrico preciso es una habilidad útil e importante; hace mucho más fácil estimar, predecir y, por lo tanto, calcular el campo eléctrico de una carga fuente. La mejor manera de desarrollar esta habilidad es con el software que te permite colocar cargas fuente y luego dibujar el campo pedido. Te recomendamos encarecidamente que busques un programa en Internet o uses la escena interactiva anterior o la que proponemos al final de este apartado. Ejecuta varias simulaciones para obtener las ideas esenciales de la construcción del diagrama de campo. Luego practica dibujando diagramas de campo y verificando tus predicciones con los diagramas dibujados en las escenas interactivas.
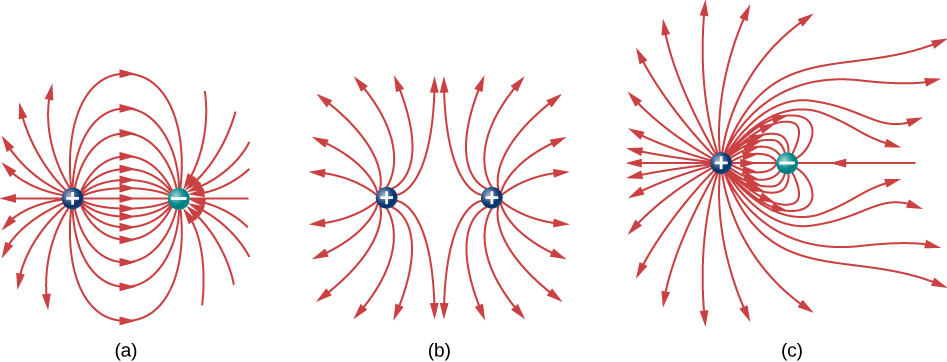
En la siguiente escena interactiva de PhET Simulaciones, mueve las cargas positivas y negativas alrededor del campo de juego y ve el campo eléctrico y el potencial electrostático. Traza las líneas equipotenciales y descubre su relación con el campo eléctrico. ¡Crea modelos de dipolos, condensadores y mucho más!
Algunas utilidades de esta escena interactiva, las comprenderás en los apartados siguientes. Por ahora, practica lo aprendido sobre campos eléctrico
Anteriormente discutimos y calculamos el campo eléctrico de un dipolo: dos cargas iguales y opuestas que están "cerca" entre sí (en este contexto, "cerrar" significa que la distancia d entre las dos cargas es mucho, mucho menor que la distancia del punto de campo P, la ubicación donde se calcula el campo). Consideremos ahora qué ocurre con un dipolo cuando se coloca en un campo externo $\overrightarrow{\bold{E}}$. Suponemos que el dipolo es un dipolo permanente; existe sin el campo, y no se rompe en el campo externo.
Por ahora, nos ocupamos solo del caso más simple: el campo externo es uniforme en el espacio. Supongamos que tenemos la situación representada en la , donde denotamos la distancia entre las cargas como el vector $\overrightarrow{\bold{d}}$, apuntando desde la carga negativa a la carga positiva. Las fuerzas en las dos cargas son iguales y opuestas, por lo que no hay fuerza neta en el dipolo. Sin embargo, hay un par:
$$\begin{align*} \overrightarrow{τ} &= (\overrightarrow{\bold{d}}/2 × \overrightarrow{\bold{F}}_+) + (−\overrightarrow{\bold{d}}/2 × \overrightarrow{\bold{F}}_−) \\ &= \left[(\overrightarrow{\bold{d}}/2) × (+q\overrightarrow{\bold{E}}) + (-\overrightarrow{\bold{d}}/2) × (-q\overrightarrow{\bold{E}}) \right] \\ &= q\overrightarrow{\bold{d}} × \overrightarrow{\bold{E}} \end{align*}$$La cantidad $q\overrightarrow{\bold{d}}$ (la magnitud de cada carga multiplicada por la distancia del vector entre ellos) es una propiedad del dipolo; su valor, como puedes ver, determina el torque que experimenta el dipolo en el campo externo. Por lo tanto, es útil definir este producto como el llamado momento dipolar del dipolo:
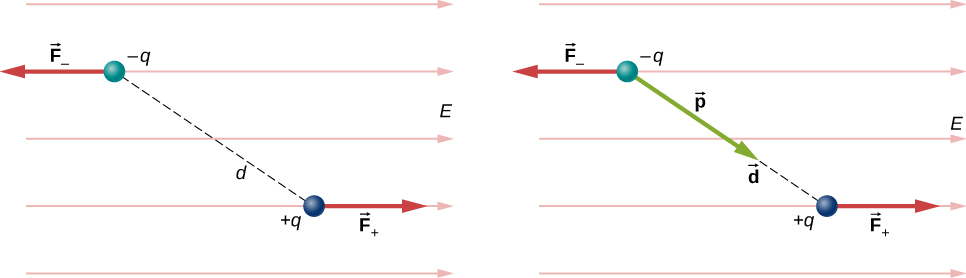
Por lo tanto, podemos escribir
Recuerda que un par cambia la velocidad angular de un objeto, el dipolo, en este caso. En esta situación, el efecto es rotar el dipolo (es decir, alinear la dirección de $\overrightarrow{\bold{p}}$) de modo que sea paralelo a la dirección del campo externo.
Los átomos neutros son, por definición, eléctricamente neutrales, tienen la misma cantidad de carga positiva y negativa.
Además, dado que son esféricamente simétricos, no tienen un momento dipolar "incorporado" como lo hacen la mayoría de las moléculas asimétricas. Obtienen uno, sin embargo, cuando se colocan en un campo eléctrico externo, porque el campo externo causa fuerzas opuestas dirigidas sobre el núcleo positivo del átomo frente a los electrones negativos que rodean el núcleo. El resultado es una nueva distribución de carga del átomo y, por lo tanto, un momento dipolar inducido ().
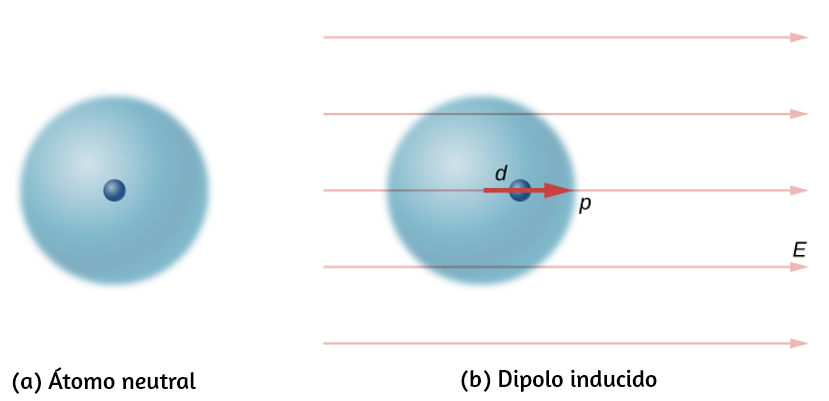
Un hecho importante aquí es que, al igual que para una molécula polar rotada, el resultado es que el momento dipolar termina alineado paralelo al campo eléctrico externo. En general, la magnitud de un dipolo inducido es mucho menor que la de un dipolo inherente.
Para ambos tipos de dipolos, observa que una vez que se completa la alineación del dipolo (girado o inducido), el efecto neto es disminuir el campo eléctrico total $\overrightarrow{\bold{E}}_{\textsf{total}} = \overrightarrow{\bold{E}}_{\textsf{externo}} + \overrightarrow{\bold{E}}_{\textsf{dipolo}}$ en las regiones dentro de las cargas del dipolo (). Por "dentro" queremos decir entre las cargas. Este efecto es crucial para los condensadores, como verás en Capacitancia.
Recuerda que encontramos el campo eléctrico de un dipolo en la Ecuación 5.7. Si lo reescribimos en términos del momento dipolar obtenemos:
$$\overrightarrow{\bold{E}} = \frac{1}{4πε_0}\frac{\overrightarrow{\bold{P}}}{z^3}$$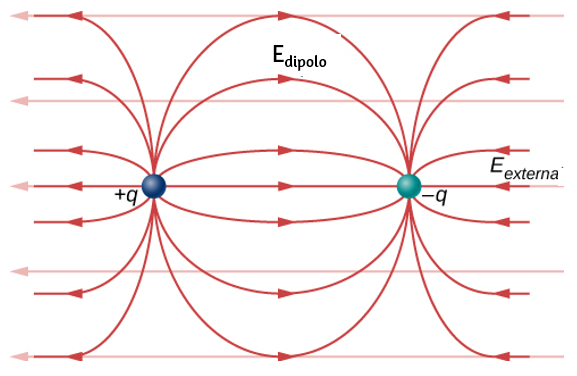
La forma de este campo se muestra en la . Ten en cuenta que a lo largo del plano perpendicular al eje del dipolo y a mitad de camino entre las cargas, la dirección del campo eléctrico es opuesta a la del dipolo y se vuelve más débil cuanto más lejos del eje se va. De forma similar, en el eje del dipolo, el campo apunta en la misma dirección que el dipolo, volviéndose más débil cuanto más se obtiene de las cargas. En la escena interactiva, diseñada por Wolfgang Christian y Anne J Cox , se muestra un dipolo. Agrega varias cargas de prueba. Describe el movimiento de algunos de las cargas de prueba (para ello, haz clic en "play").

El flujo es un concepto general y ampliamente aplicable en física. Sin embargo, en este capítulo, nos concentraremos en el flujo del campo eléctrico. Esto nos permite introducir la ley de Gauss, que es particularmente útil para encontrar los campos eléctricos de las distribuciones de carga que exhiben simetría espacial. Los principales temas discutidos aquí son
Hasta ahora, hemos encontrado que el campo electrostático comienza y termina en cargas puntuales y que el campo de una carga puntual varía inversamente al cuadrado de la distancia de esa carga. Estas características del campo electrostático conducen a una relación matemática importante conocida como la ley de Gauss. Esta ley se llama en honor al extraordinario matemático y científico alemán Karl Friedrich Gauss (). La ley de Gauss nos brinda una forma elegantemente simple de encontrar el campo eléctrico y, como verás, puede ser mucho más fácil de usar que el método de integración descrito en el capítulo anterior. Sin embargo, hay una trampa: la ley de Gauss tiene una limitación porque, aunque siempre es cierta, puede aplicarse fácilmente solo para distribuciones de carga con ciertas simetrías.
El concepto de flujo describe cuánto de algo pasa por un área determinada. Más formalmente, es el producto escalar de un campo vectorial (en este capítulo, el campo eléctrico) con un área. Puedes conceptualizar el flujo de un campo eléctrico como una medida del número de líneas de campo eléctrico que pasan a través de un área ().
Cuanto más grande es el área, más líneas de campo pasan por ella y, por lo tanto, mayor es el flujo; de manera similar, cuanto más fuerte es el campo eléctrico (representado por una mayor densidad de líneas), mayor es el flujo.

Por otro lado, si el área gira para que el campo esté alineado con las líneas de campo, ninguna pasará y no habrá flujo.
Una analogía macroscópica que podría ayudarte a imaginar esto es poner un hula hula en un río que fluye. A medida que cambia el ángulo del aro en relación con la dirección de la corriente, más o menos del flujo pasará por el aro. Del mismo modo, la cantidad de flujo a través del aro depende de la fuerza de la corriente y el tamaño del aro.
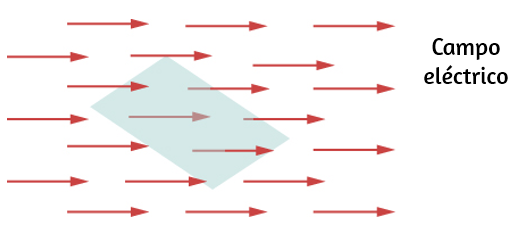
Nuevamente, el flujo es un concepto general; también podemos usarlo para describir la cantidad de luz solar que golpea un panel solar o la cantidad de energía que recibe un telescopio de una estrella distante, por ejemplo.
Para cuantificar esta idea, la (a) muestra una superficie plana $S_1$ de área $A_1$ que es perpendicular al campo eléctrico uniforme $\overrightarrow{\bold{E}} = E\^{y}$. Si $N$ líneas de campo pasan a través de $S_1$, entonces sabemos por la definición de líneas de campo eléctrico que $N/A_1 α E$ o $N α EA_1$.
La cantidad $EA_1$ es el flujo eléctrico a través de $S_1$. Representamos el flujo eléctrico a través de una superficie abierta como $S_1$ con el símbolo $Φ$. El flujo eléctrico es una cantidad escalar y tiene una unidad del SI de newton-metros cuadrados por culombio ($N \cdot m^2/C$). Observa que $N α EA_1$ también se puede escribir como $N α Φ$, lo que demuestra que el flujo eléctrico es una medida del número de líneas de campo que cruzan una superficie.
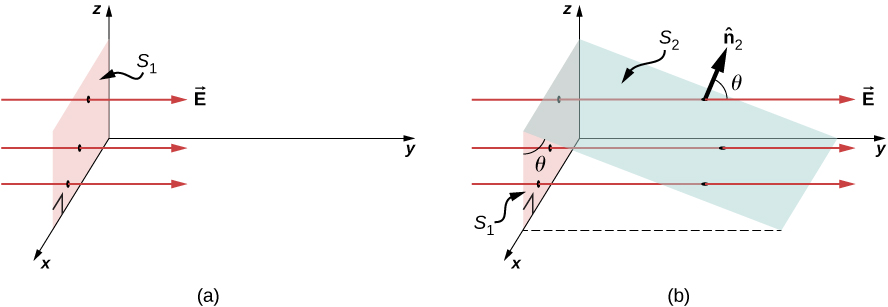
Ahora, considera una superficie plana que no es perpendicular al campo. ¿Cómo representaríamos el flujo eléctrico? La (b) muestra una superficie $S_2$ de área $A_2$ inclinada en un ángulo $θ$ al plano $xz$ y cuya proyección en ese plano es $S_1$ (área $A_1$). Las áreas están relacionadas por $A_2cosθ = A_1$. Debido a que el mismo número de líneas de campo cruza tanto $S_1$ como $S_2$, los flujos a través de ambas superficies deben ser iguales. El flujo a través de $S_2$ es por lo tanto $Φ = EA_1 = EA_2cosθ$. Designando $\^{n}_2$ como un vector unitario normal a $S_2$ (ver ), obtenemos
$$Φ = \overrightarrow{\bold{E}} \cdot \^{n}_2A_2$$Echa un vistazo al siguiente vídeo para observar lo que sucede con el flujo a medida que el área cambia de tamaño y ángulo, o el campo eléctrico cambia de intensidad.
El flujo eléctrico es proporcional a la cantidad de líneas de campo eléctrico que atraviesan una superficie. Esta animación ilustra los 3 parámetros que influyen en el flujo eléctrico: el área de la superficie atravesada por líneas de campo eléctrico, la magnitud del campo eléctrico y el ángulo entre el campo eléctrico y la superficie. En la animación, las líneas del campo eléctrico son verdes cuando cruzan la superficie y se vuelven amarillas cuando no cruzan la superficie.
Para discutir el flujo de un campo vectorial, es útil introducir un vector de área $\overrightarrow{\bold{A}}$. Esto nos permite escribir la última ecuación en una forma más compacta. ¿Cuál debería ser la magnitud del vector de área? ¿Cuál debería ser la dirección del vector de área? ¿Cuáles son las implicaciones de tus respuestas a la pregunta anterior?
El vector de área de una superficie plana de área $A$ tiene la siguiente magnitud y dirección:
Como la superficie normal al plano puede apuntar en cualquier dirección desde la superficie, se debe elegir la dirección del vector de área de una superficie abierta, como se muestra en la
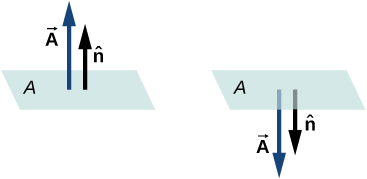
Como $\^{n}$ es una unidad normal a una superficie, tiene dos direcciones posibles en cada punto de esa superficie ( (a)). Para una superficie abierta, podemos usar cualquier dirección, siempre que seamos consistentes sobre toda la superficie. La parte (c) de la figura muestra varios casos.
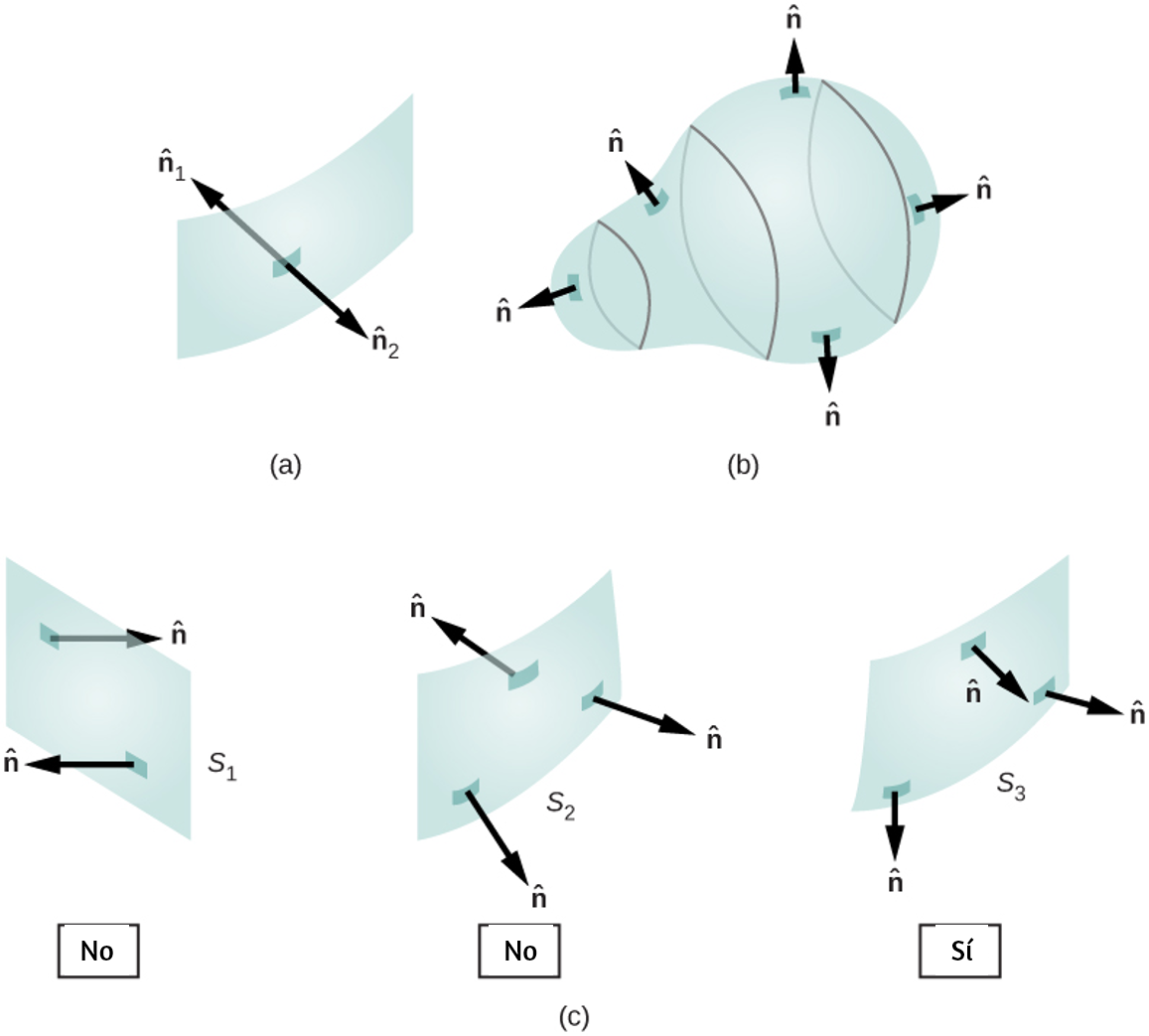
Sin embargo, si una superficie está cerrada, entonces la superficie encierra un volumen. En ese caso, la dirección del vector normal en cualquier punto de la superficie apunta desde el interior hacia el exterior. En una superficie cerrada como la de la (b), $\^{n}$ se elige como la normal hacia afuera en cada punto, para ser consistente con la convención de signos de carga eléctrica.
Ahora que hemos definido el vector de área de una superficie, podemos definir el flujo eléctrico de un campo eléctrico uniforme a través de un área plana como el producto escalar del campo eléctrico y el vector de área, como se define en Productos de Vectores:
La muestra el campo eléctrico de un sistema de placas paralelas con carga opuesta y una caja imaginaria entre las placas. El campo eléctrico entre las placas es uniforme y apunta desde la placa positiva hacia la placa negativa. Un cálculo del flujo de este campo a través de varias caras de la caja muestra que el flujo neto a través de la caja es cero. ¿Por qué el flujo se cancela aquí?
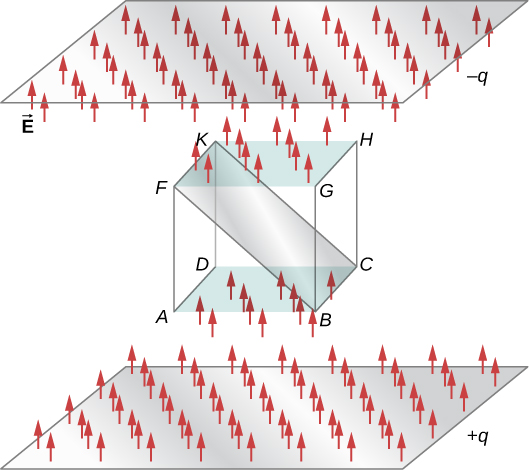
La razón es que las fuentes del campo eléctrico están fuera de la caja. Por lo tanto, si cualquier línea de campo eléctrico ingresa al volumen de la caja, también debe salir a alguna parte de la superficie porque no hay carga adentro para que las líneas aterricen. Por lo tanto, generalmente, el flujo eléctrico a través de una superficie cerrada es cero si no hay fuentes de campo eléctrico, ya sean cargas positivas o negativas, dentro del volumen adjunto.
En general, cuando las líneas de campo salen (o "fluyen de afuera") de una superficie cerrada, $Φ$ es positiva; cuando entran (o "fluyen hacia") la superficie, $Φ$ es negativo.
Cualquier superficie lisa y no plana puede reemplazarse por una colección de superficies pequeñas, aproximadamente planas, como se muestra en la . Si dividimos superficie S en pequeños parches, notamos que, a medida que los parches se hacen más pequeños, pueden aproximarse por superficies planas. Esto es similar a la forma en que tratamos la superficie de la Tierra como localmente plana, a pesar de que sabemos que a nivel mundial, es aproximadamente esférica.
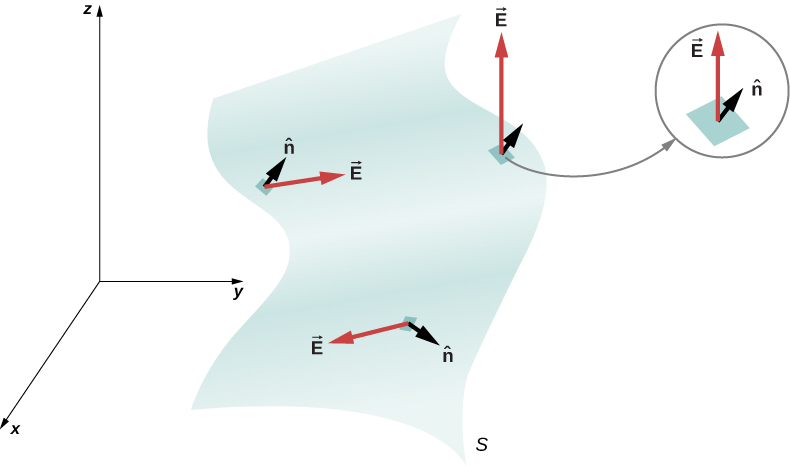
Para realizar un seguimiento de los parches, podemos numerarlos del $1$ al $N$. Ahora, definimos el vector de área para cada parche como el área del parche apuntando en la dirección de la normal.
Denotemos el vector de área para el i-ésimo parche por $Δ\overrightarrow{\bold{A}}_i$ (Hemos utilizado el símbolo $Δ$ para recordarnos que el área es de un parche arbitrariamente pequeño). Con parches suficientemente pequeños, podemos aproximar el campo eléctrico sobre cualquier parche dado como uniforme. Denotemos el campo eléctrico promedio en la ubicación del $i$-ésimo parche por $\overrightarrow{\bold{E}}_i$.
$$\overrightarrow{\bold{E}}_i = \textsf{campo eléctrico promedio sobre el parche }i\textsf{-ésimo}$$Por lo tanto, podemos escribir el flujo eléctrico $Φ_i$ a través del área del $i$-ésimo parche como
$$Φ_i = \overrightarrow{\bold{E}}_i \cdot Δ\overrightarrow{\bold{A}}_i (\textsf{parche }i\textsf{-ésimo})$$El flujo a través de cada parche individual puede construirse de esta manera y luego agregarse para darnos una estimación del flujo neto a través de toda la superficie $S$, que denotamos simplemente como $Φ$.
$$Φ = \sum_{i=1}^{N} Φ_i = \sum_{i=1}^{N} \overrightarrow{\bold{E}}_i \cdot Δ\overrightarrow{\bold{A}}_i$$Esta estimación del flujo mejora a medida que disminuimos el tamaño de los parches. Sin embargo, cuando utilizas parches más pequeños, necesitas más de ellos para cubrir la misma superficie. En el límite de parches infinitesimalmente pequeños, se puede considerar que tienen un área $dA$ y una unidad normal $\^{n}$.
Como los elementos son infinitesimales, se puede suponer que son planos, y $\overrightarrow{\bold{E}}_i$ se puede tomar como constante sobre cualquier elemento. Entonces el flujo $dΦ$ a través de un área $dA$ viene dado por $dΦ = \overrightarrow{\bold{E}} \cdot \^{n}dA$. Es positivo cuando el ángulo entre $\overrightarrow{\bold{E}}_i$ y $\^{n}$ es menor que $90°$ y negativo cuando el ángulo es mayor que $90°$.
El flujo neto es la suma de los elementos de flujo infinitesimal en toda la superficie. Con parches infinitesimalmente pequeños, necesitas infinitos parches, y el límite de la suma se convierte en una integral de superficie. Con $\int_S$ representando la integral sobre $S$,
En términos prácticos, las integrales de superficie se calculan tomando las antiderivadas de ambas dimensiones que definen el área, con los bordes de la superficie en cuestión como los límites de la integral. Para distinguir entre el flujo a través de una superficie abierta como la de la y el flujo a través de una superficie cerrada (una que limita por completo algún volumen), representamos el flujo a través de una superficie cerrada por
donde el círculo a través del símbolo integral simplemente significa que la superficie está cerrada, y estamos integrando sobre todo. Si solo se integra en una parte de una superficie cerrada, eso significa que está tratando un subconjunto de ella como una superficie abierta.
Ejemplo 6.1
Flujo de un campo eléctrico uniforme
Un campo eléctrico constante de magnitud $E_0$ apunta en la dirección del eje $z$ positivo (). ¿Cuál es el flujo eléctrico a través de un rectángulo con lados $a$ y $b$ en el plano (a) $xy$ y en el plano (b) $xz$?
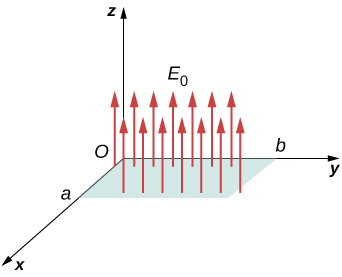
Estrategia
Aplicar la definición de flujo: $Φ = \overrightarrow{\bold{E}} \cdot \overrightarrow{\bold{A}} (\overrightarrow{\bold{E}} \textsf{uniforme})$, donde la definición de producto escalar es crucial.
Solución
En este caso, $Φ = \overrightarrow{\bold{E}}_0 \cdot \overrightarrow{\bold{A}} = E_0A = E_0ab$.
Aquí, la dirección del vector de área es a lo largo del eje y positivo o hacia el eje y negativo. Por lo tanto, el producto escalar del campo eléctrico con el vector de área es cero, dando un flujo cero.
Explicación
Las direcciones relativas del campo eléctrico y el área pueden causar que el flujo a través del área sea cero.
Ejemplo 6.2
Flujo de un campo eléctrico uniforme a través de una superficie cerrada
Un campo eléctrico constante de magnitud $E_0$ apunta en la dirección del eje $z$ positivo (). ¿Cuál es el flujo eléctrico neto a través de un cubo?
Estrategia
Aplica la definición de flujo: $Φ = \overrightarrow{\bold{E}} \cdot \overrightarrow{\bold{A}} (\overrightarrow{\bold{E}} \textsf{uniforme})$, y observa que una superficie cerrada elimina la ambigüedad en la dirección del vector de área.
Solución
A través de la cara superior del cubo, $Φ = \overrightarrow{\bold{E}}_0 \cdot \overrightarrow{\bold{A}} = E_0A$.
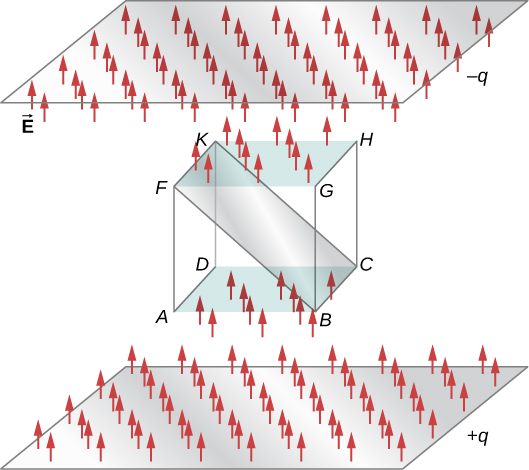
A través de la cara inferior del cubo, $Φ = \overrightarrow{\bold{E}}_0 \cdot \overrightarrow{\bold{A}} = -E_0A$, porque el vector de área aquí apunta hacia abajo.
A lo largo de los otros cuatro lados, la dirección del vector de área es perpendicular a la dirección del campo eléctrico. Por lo tanto, el producto escalar del campo eléctrico con el vector de área es cero, dando un flujo cero.
El flujo neto es $Φ_{\textsf{neto}} = E_0A - E_0A + 0 + 0 + 0 + 0 = 0$.
Explicación
El flujo neto de un campo eléctrico uniforme a través de una superficie cerrada es cero.
Ejemplo 6.3
Flujo eléctrico a través de un avión, método integral
Un campo eléctrico uniforme $\overrightarrow{\bold{E}}$ de magnitud $10 N/C$ se dirige en paralelo al plano $yz$ a $30°$ por encima del plano $xy$, como se muestra en la . ¿Cuál es el flujo eléctrico a través de la superficie del plano de $6.0 m^2$ ubicado en el plano $xz$? Supongamos que $\^{n}$ apunta en la dirección positiva de $y$.
Estrategia
Aplica $Φ = \int_S\overrightarrow{\bold{E}} \cdot \^{n}dA$, donde la dirección y la magnitud del campo eléctrico son constantes.
Solución
El ángulo entre el campo eléctrico uniforme $\overrightarrow{\bold{E}}$ y la normal unitaria $\^{n}$ a la superficie plana es de $30°$. Dado que la dirección como la magnitud son constantes, $E$ sale de la integral. Todo lo que queda es una integral de superficie sobre $dA$, que es $A$. Por lo tanto, usando la ecuación de superficie abierta, encontramos que el flujo eléctrico a través de la superficie es
$$Φ = \int_S \overrightarrow{\bold{E}} \cdot \^{n}d \overrightarrow{\bold{A}} = EAcosθ$$ $$Φ = (10 N/C)(6.0 m^2)(cos 30°) = 52 N \cdot m^2/C$$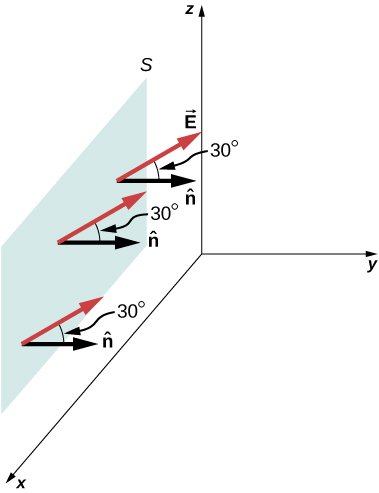
Explicación
De nuevo, las direcciones relativas del campo y el área importan, y la ecuación general con la integral se simplificará al producto punto simple de área y campo eléctrico.
 Comprueba tu aprendizaje 6.1
Comprueba tu aprendizaje 6.1
Ejemplo 6.4
Campo eléctrico no homogéneo
¿Cuál es el flujo total del campo eléctrico $\overrightarrow{\bold{E}} = cy^2\^{k}$ a través de la superficie rectangular que se muestra en la ?
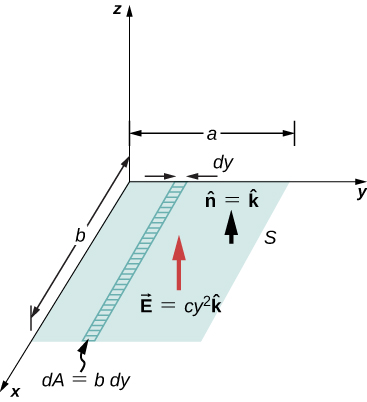
Estrategia
Aplica $Φ = \int_S\overrightarrow{\bold{E}} \cdot \^{n}dA$. Suponemos que la normal unitaria $\^{n}$ a la superficie determinada apunta en la dirección $z$ positiva, entonces $\^{n} = \^{k}$. Dado que el campo eléctrico no es uniforme sobre la superficie, es necesario dividir la superficie en franjas infinitesimales a lo largo de las cuales $\overrightarrow{\bold{E}}$ es esencialmente constante. Como se muestra en la , estas franjas son paralelas al eje $x$, y cada franja tiene un área $dA = bdy$.
Solución
Desde la integral de superficie abierta, encontramos que el flujo neto a través de la superficie rectangular es
$$\begin{align*} Φ &= \int_S\overrightarrow{\bold{E}} \cdot \^{n}dA = \int_0^a (cy^2\^{k}) \cdot \^{k}(bdy) \\ &= cb\int_0^a y^2dy = \frac{1}{3}a^3bc \end{align*}$$Explicación
Para un campo eléctrico no constante, se requiere el método de la integral.
 Comprueba tu aprendizaje 6.2
Comprueba tu aprendizaje 6.2
Ahora podemos determinar el flujo eléctrico a través de una superficie cerrada arbitraria debido a una distribución de carga arbitraria. Descubrimos que si una superficie cerrada no tiene carga dentro donde una línea de campo eléctrico puede terminar, entonces cualquier línea de campo eléctrico que entre en la superficie en un punto debe necesariamente salir en algún otro punto de la superficie. Por lo tanto, si una superficie cerrada no tiene cargas dentro del volumen incluido, entonces el flujo eléctrico a través de la superficie es cero. Ahora, ¿qué le sucede al flujo eléctrico si hay algunas cargas dentro del volumen incluido? La ley de Gauss da una respuesta cuantitativa a esta pregunta.
Para tener una idea de qué esperar, calculemos el flujo eléctrico a través de una superficie esférica alrededor de una carga puntual positiva $q$, ya que conocemos el campo eléctrico en tal situación. Recuerda que cuando colocamos la carga puntual en el origen de un sistema de coordenadas, el campo eléctrico en un punto $P$ que está a una distancia $r$ de la carga en el origen viene dado por
$$\overrightarrow{\bold{E}}_P = \frac{1}{2πε_0}\frac{1}{r^2}\^{r}$$donde $\^{r}$ es el vector radial desde la carga en el origen hasta el punto $P$. Podemos usar este campo eléctrico para encontrar el flujo a través de la superficie esférica del radio $r$, como se muestra en la figura .
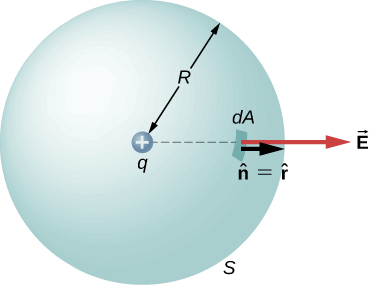
Luego aplicamos $Φ = \int_S\overrightarrow{\bold{E}} \cdot \^{n}dA$ a este sistema y sustituimos los valores conocidos. En la esfera, $\^{n} = \^{r}$ y $r = R$, por lo que para un área infinitesimal $dA$,
$$dΦ = \overrightarrow{\bold{E}} \cdot \^{n}dA = \frac{1}{4πε_0}\frac{q}{R^2}\^{r}\^{r}dA = \frac{1}{4πε_0}\frac{q}{R^2}dA$$Ahora encontramos el flujo neto al integrar este flujo sobre la superficie de la esfera:
$$Φ = \frac{1}{4πε_0}\frac{q}{R^2}\int_SdA = \frac{1}{4πε_0}\frac{q}{R^2}(4πR^2) = \frac{q}{ε_0}$$donde el área superficial total de la superficie esférica es $4πR^2$. Esto proporciona el flujo a través de la superficie esférica cerrada al radio $r$ como
$$Φ = \frac{q}{ε_0} \tag{6.4}$$Un hecho notable sobre esta ecuación es que el flujo es independiente del tamaño de la superficie esférica. Esto se puede atribuir directamente al hecho de que el campo eléctrico de una carga puntual disminuye como $1/r^2$ con la distancia, lo que simplemente cancela la tasa de aumento de la superficie de $r^2$.
Una forma alternativa de ver por qué el flujo a través de una superficie esférica cerrada es independiente del radio de la superficie es observar las líneas del campo eléctrico. Ten en cuenta que cada línea de campo de q atraviesa la superficie en el radio $R_1$ también perfora la superficie en $R_2$ ().
Por lo tanto, el número neto de líneas de campo eléctrico que pasan a través de las dos superficies desde el interior hacia el exterior es igual. Este número neto de líneas de campo eléctrico, que se obtiene al restar el número de líneas en la dirección desde el exterior al interior desde el número de líneas en la dirección desde el interior al exterior, proporciona una medida visual del flujo eléctrico a través de las superficies.
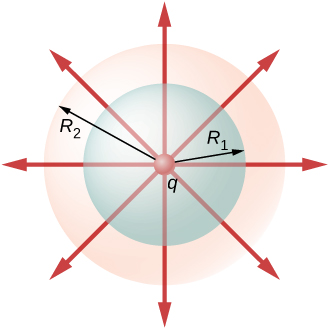
Puede ver que si no se incluyen cargas dentro de una superficie cerrada, entonces el flujo eléctrico a través de ella debe ser cero. Una línea de campo típica ingresa a la superficie en $dA_2$ y sale en $dA_2$. Cada línea que entre a la superficie también debe abandonar esa superficie. Por lo tanto, el "flujo" neto de las líneas de campo dentro o fuera de la superficie es cero ( (a)). Lo mismo sucede si se incluyen cargas de signo igual y opuesto dentro de la superficie cerrada, de modo que la carga total incluida es cero (parte (b)). Una superficie que incluye la misma cantidad de carga tiene el mismo número de líneas de campo que la cruzan, independientemente de la forma o el tamaño de la superficie, siempre que la superficie contenga la misma cantidad de carga (parte (c)).
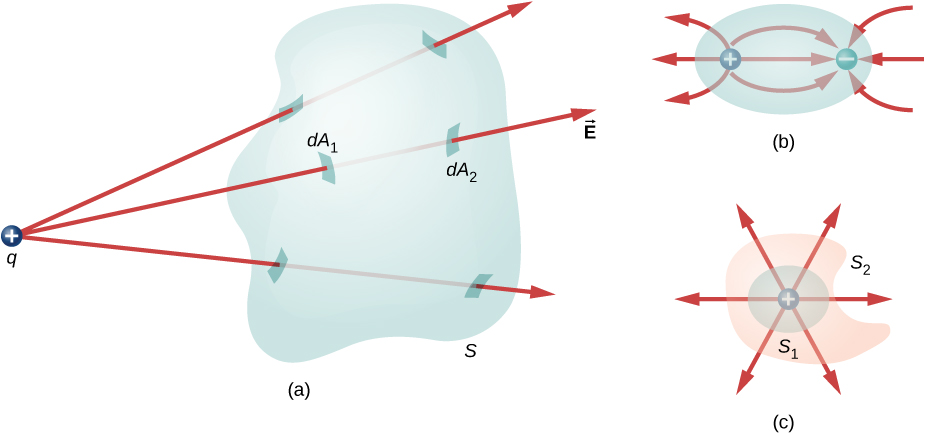
La ley de Gauss generaliza este resultado al caso de cualquier cantidad de cargas y cualquier ubicación de las cargas en el espacio dentro de la superficie cerrada. De acuerdo con la ley de Gauss, el flujo del campo eléctrico $\overrightarrow{\bold{E}}$ a través de cualquier superficie cerrada, también llamada superficie gaussiana, es igual a la carga neta encerrada ($q_{\textsf{enc}}$) dividida por la permitividad del espacio libre ($ε_0$):
$$Φ_{\textsf{Superficie cerrada}} = \frac{q_{\textsf{enc}}}{ε_0}$$Esta ecuación se cumple para las cargas de cualquiera de los signos, porque definimos el vector de área de una superficie cerrada para señalar hacia afuera. Si la carga adjunta es negativa (ver (b)), entonces el flujo a través de $S$ o $S'$ es negativo.
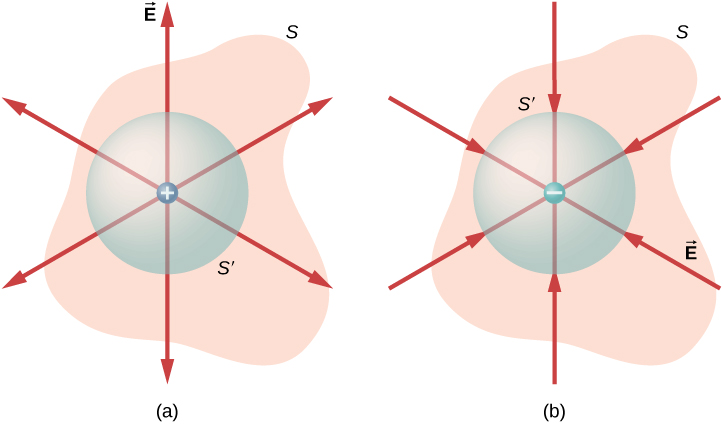
La superficie gaussiana no necesita corresponderse con un objeto físico real; de hecho, raramente lo hará. Es una construcción matemática que puede tener cualquier forma, siempre que esté cerrada. Sin embargo, dado que nuestro objetivo es integrar el flujo sobre él, tendemos a elegir formas que son altamente simétricas.
Si las cargas son puntos discretos, entonces simplemente las agregamos. Si la carga se describe mediante una distribución continua, entonces debemos integrarla adecuadamente para encontrar la carga total que reside dentro del volumen adjunto. Por ejemplo, el flujo a través de la superficie Gaussiana $S$ de la es $Φ = (q_1 + q_2 + q_5)/ε_0$. Ten en cuenta que $q_{\textsf{enc}}$ es simplemente la suma de las cargas puntuales. Si la distribución de carga fuera continua, necesitaríamos integrarla apropiadamente para calcular la carga total dentro de la superficie gaussiana.
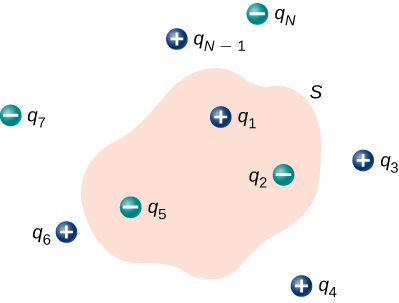
Recuerda que el principio de superposición se aplica al campo eléctrico. Por lo tanto, el campo eléctrico total en cualquier punto, incluidos los de la superficie gaussiana elegida, es la suma de todos los campos eléctricos presentes en este punto. Esto nos permite escribir la ley de Gauss en términos del campo eléctrico total.
Ley de gauss
El flujo $Φ$ del campo eléctrico $\overrightarrow{\bold{E}}$ a través de cualquier superficie cerrada $S$ (una superficie gaussiana) es igual a la carga neta encerrada ($q_{\textsf{enc}}$) dividida por la permitividad del espacio libre $(ε_0)$:
$$Φ = \oint_S \overrightarrow{\bold{E}} \cdot \^{n}d \overrightarrow{\bold{A}} = \frac{q_{\textsf{enc}}}{ε_0} \tag{6.5}$$Para usar la ley de Gauss de manera efectiva, debes tener una comprensión clara de lo que representa cada término en la ecuación. El campo $\overrightarrow{\bold{E}}$ es el campo eléctrico total en cada punto de la superficie gaussiana. Este campo total incluye contribuciones de cargas tanto dentro como fuera de la superficie de Gauss. Sin embargo, $q_{\textsf{enc}}$ es solo la carga dentro de la superficie de Gauss. Finalmente, la superficie gaussiana es cualquier superficie cerrada en el espacio. Esa superficie puede coincidir con la superficie real de un conductor, o puede ser una superficie geométrica imaginaria. El único requisito impuesto sobre una superficie Gaussiana es que esté cerrada ().
Ejemplo 6.5
Flujo eléctrico a través de superficies Gaussianas
Calcula el flujo eléctrico a través de cada superficie Gaussiana que se muestra en la .
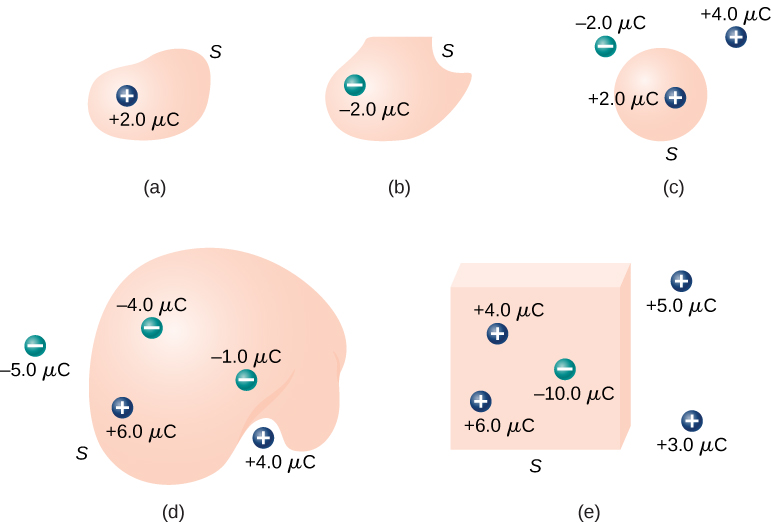
Estrategia
Según la ley de Gauss, el flujo a través de cada superficie viene dado por $q_{\textsf{enc}}/ε_0$, donde $q_{\textsf{enc}}$ es la carga encerrada por esa superficie.
Solución
Para las superficies y cargas que se muestran, encontramos
a. $Φ = \dfrac{2.0 μC}{ε_0} = 2.3 × 10^5 N \cdot m^2/C$.
b. $Φ = \dfrac{- 2.0 μC}{ε_0} = - 2.3 × 10^5 N \cdot m^2/C$.
c. $Φ = \dfrac{2.0 μC}{ε_0} = 2.3 × 10^5 N \cdot m^2/C$.
d. $Φ = \dfrac{- 4.0 μC + 6.0 μC -1.0 μC}{ε_0} = 1.1 × 10^5 N \cdot m^2/C$.
e. $Φ = \dfrac{4.0 μC + 6.0 μC -10.0 μC}{ε_0} = 0$
Explicación
En el caso especial de una superficie cerrada, los cálculos de flujo se convierten en una suma de cargas. En la siguiente sección, esto nos permitirá trabajar con sistemas más complejos.
 Comprueba tu aprendizaje 6.3
Comprueba tu aprendizaje 6.3
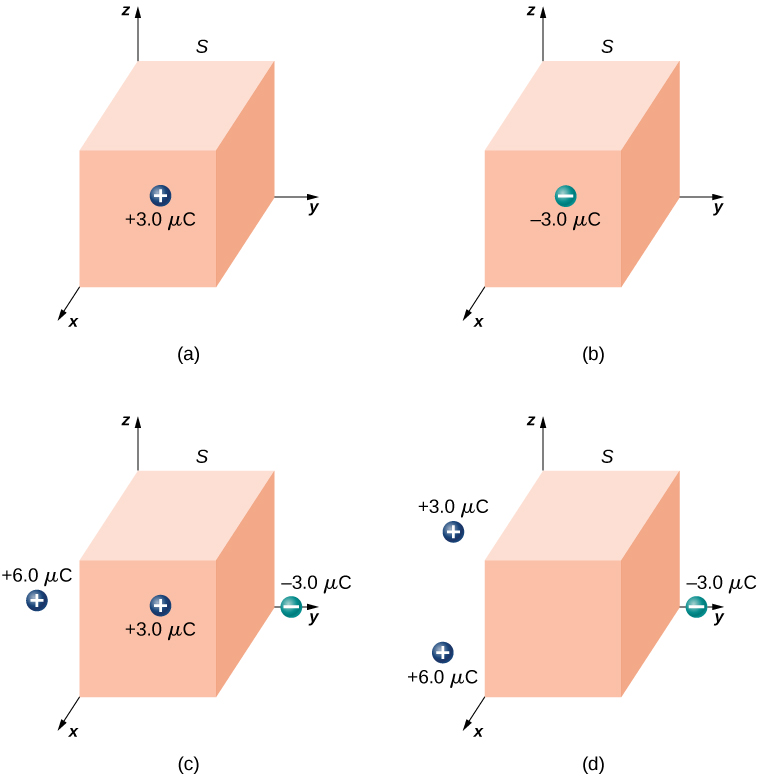
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, ajusta la magnitud de la carga y el radio de la superficie gaussiana a su alrededor. Observa cómo esto afecta el flujo total y la magnitud del campo eléctrico en la superficie gaussiana.
Las flechas representan la magnitud y dirección del campo eléctrico generado por la partícula. Puedes cambiar el radio de la superficie gaussiana y la carga. Puedes, también, rotar el cubo con clic sostenido. La escena se diseñó a partir del objeto diseñado por Andrew Duffy y Renee Sweeney en the Boston University Physics Department
La ley de Gauss es muy útil para determinar expresiones para el campo eléctrico, aunque la ley no se refiere directamente al campo eléctrico; se trata del flujo eléctrico. Resulta que en situaciones que tienen ciertas simetrías (esféricas, cilíndricas o planas) en la distribución de carga, podemos deducir el campo eléctrico basado en el conocimiento del flujo eléctrico.
En estos sistemas, podemos encontrar una superficie Gaussiana $S$ sobre la cual el campo eléctrico tiene una magnitud constante. Además, si $\overrightarrow{\bold{E}}$ es paralelo a $\^{n}$ en todas partes en la superficie, entonces $\overrightarrow{\bold{E}} \cdot \^{n} = E$ (Si $\overrightarrow{\bold{E}}$ y $\^{n}$ son antiparalelos en todas partes en la superficie, entonces $\overrightarrow{\bold{E}} \cdot \^{n} = -E$). La ley de Gauss se simplifica a
donde $A$ es el área de la superficie. Ten en cuenta que estas simetrías conducen a la transformación de la integral de flujo en un producto de la magnitud del campo eléctrico y un área apropiada. Cuando usas este flujo en la expresión de la ley de Gauss, obtienes una ecuación algebraica que puedes resolver para la magnitud del campo eléctrico, que se ve como
$$E ∝ \frac{q_{\textsf{enc}}}{ε_0\textsf{Área}}$$La dirección del campo eléctrico en el punto de campo $P$ se obtiene a partir de la simetría de la distribución de carga y el tipo de carga en la distribución.
Por lo tanto, la ley de Gauss se puede usar para determinar $\overrightarrow{\bold{E}}$. Aquí hay un resumen de los pasos que seguiremos:
Estrategia de resolución de problemas: Ley de Gauss
1. Identifica la simetría espacial de la distribución de carga. Este es un primer paso importante que nos permite elegir la superficie Gaussiana apropiada. Como ejemplos, una carga puntual aislada tiene simetría esférica, y una línea infinita de carga tiene simetría cilíndrica.
2. Elige una superficie gaussiana con la misma simetría que la distribución de carga e identifica sus resultados. Con esta opción, $\overrightarrow{\bold{E}} \cdot \^{n}$ se determina fácilmente sobre la superficie gaussiana.
3. Evalúa la integral $\oint_S \overrightarrow{\bold{E}} \cdot \^{n}d \overrightarrow{\bold{A}}$ sobre la superficie gaussiana, es decir, calcula el flujo a través de la superficie. La simetría de la superficie gaussiana nos permite factorizar $\overrightarrow{\bold{E}} \cdot \^{n}$ fuera de la integral.
4. Determina la cantidad de carga encerrada por la superficie gaussiana. Esta es una evaluación del lado derecho de la ecuación que representa la ley de Gauss. A menudo es necesario realizar una integración para obtener la carga neta encerrada.
5. Evalúa el campo eléctrico de la distribución de carga. El campo ahora se puede encontrar usando los resultados de los pasos 3 y 4.
Básicamente, solo hay tres tipos de simetría que permiten que la ley de Gauss se use para deducir el campo eléctrico. Las cuales son:
Para aprovechar la simetría, llevamos a cabo los cálculos en los sistemas de coordenadas apropiados y usamos el tipo correcto de superficie gaussiana para esa simetría, aplicando los cuatro pasos restantes.
Una distribución de carga tiene simetría esférica si la densidad de carga depende únicamente de la distancia desde un punto en el espacio y no de la dirección. En otras palabras, si gira el sistema, no se ve diferente. Por ejemplo, si una esfera de radio R está uniformemente cargada con densidad de carga $ρ_0$, entonces la distribución tiene simetría esférica ( (a)). Por otro lado, si una esfera de radio $R$ se carga para que la mitad superior de la esfera tenga una densidad de carga uniforme $ρ_1$ y la mitad inferior tenga una densidad de carga uniforme $ρ_2 ≠ ρ_1$, entonces la esfera no tiene simetría esférica porque la densidad de carga depende de la dirección ( (b)). Por lo tanto, no es la forma del objeto sino la forma de la distribución de carga la que determina si un sistema tiene o no simetría esférica.
La muestra una esfera con cuatro capas diferentes, cada una con su propia densidad de carga uniforme. Aunque esta es una situación en la que la densidad de carga en la esfera completa no es uniforme, la función de densidad de carga depende únicamente de la distancia desde el centro y no de la dirección. Por lo tanto, esta distribución de carga tiene simetría esférica.
Una buena forma de determinar si tu problema tiene simetría esférica es observar la función de densidad de carga en coordenadas esféricas, $ρ(r, θ, φ)$.
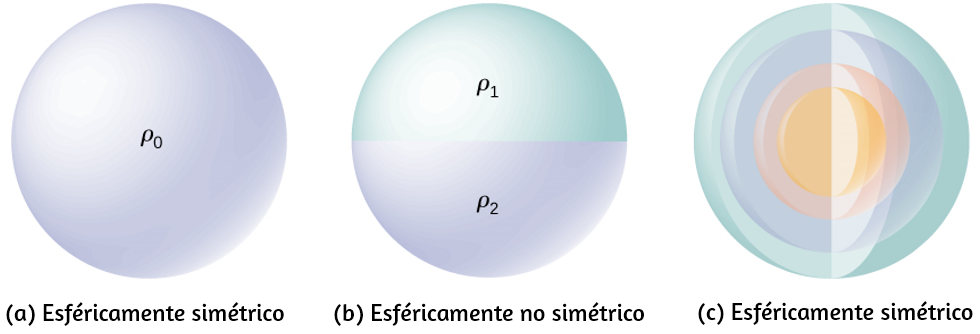
Si la densidad de carga es solo una función de $r$, eso es $ρ = ρ(r)$, entonces tienes simetría esférica. Si la densidad depende de $θ$ o $φ$, puedes cambiarla por rotación; por lo tanto, no tendrías simetría esférica.
Consecuencias de la simetría
En todos los casos esféricamente simétricos, el campo eléctrico en cualquier punto debe estar dirigido radialmente, porque la carga y, por lo tanto, el campo deben ser invariantes bajo rotación.
Por lo tanto, usando coordenadas esféricas con sus orígenes en el centro de la distribución de carga esférica, podemos escribir la forma esperada del campo eléctrico en un punto $P$ ubicado a una distancia $r$ del centro: $$\textsf{Simetría esférica}: \overrightarrow{\bold{E}}_P = E_P(r)\^{r} \tag{6.7}$$
donde $r$ es el vector unitario apuntando en la dirección desde el origen hasta el punto del campo $P$. El componente radial $E_P$ del campo eléctrico puede ser positivo o negativo. Cuando $EP > 0$, el campo eléctrico en $P$ señala lejos del origen, y cuando $EP < 0$, el campo eléctrico en $P$ apunta hacia el origen.
Cálculos gaussianos de superficie y flujo
Ahora podemos usar esta forma del campo eléctrico para obtener el flujo del campo eléctrico a través de la superficie gaussiana. Para la simetría esférica, la superficie gaussiana es una superficie esférica cerrada que tiene el mismo centro que el centro de la distribución de carga. Por lo tanto, la dirección del vector de área de un elemento de área en la superficie gaussiana en cualquier punto es paralela a la dirección del campo eléctrico en ese punto, ya que ambos están dirigidos radialmente hacia afuera ().
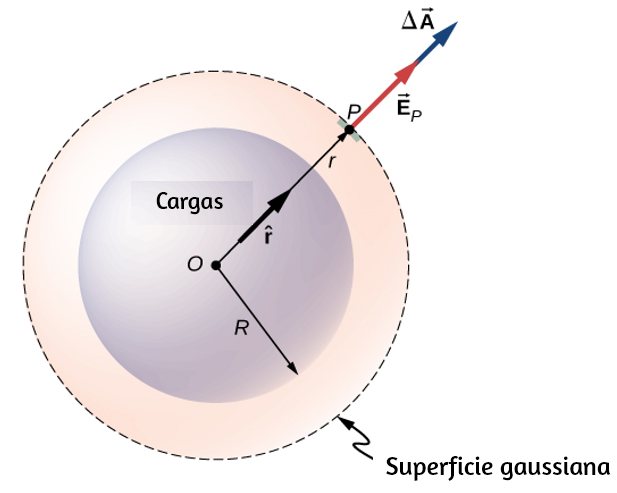
La magnitud del campo eléctrico $\overrightarrow{\bold{E}}$ debe ser la misma en todas partes en una superficie esférica Gaussiana concéntrica con la distribución. Para una superficie esférica de radio $r$,
$$Φ = \oint_S \overrightarrow{\bold{E}}_P \cdot \^{n}d\overrightarrow{\bold{A}} = E\oint_S dA = E_P4πr^2$$Usando la ley de Gauss
De acuerdo con la ley de Gauss, el flujo a través de una superficie cerrada es igual a la carga total encerrada dentro de la superficie cerrada dividida por la permitividad del vacío $ε_0$. Donde $q_{\textsf{enc}}$ es la carga total encerrada dentro de la distancia r desde el origen, que es el espacio dentro de la superficie esférica gaussiana de radio $r$. Esto da la siguiente relación para la ley de Gauss:
$$4πr^2E = \frac{q_{\textsf{enc}}}{ε_0}$$Por lo tanto, el campo eléctrico en el punto $P$ que está a una distancia $r$ del centro de una distribución de carga esféricamente simétrica tiene la siguiente magnitud y dirección:
$$\textsf{Magnitud}: E(r) = \frac{1}{4πε_0}\frac{q_{\textsf{enc}}}{r^2} \tag{6.8}$$Dirección: radial de $O$ a $P$ o de $P$ a $O$.
La dirección del campo en el punto $P$ depende de si la carga en la esfera es positiva o negativa. Para una carga positiva neta encerrada dentro de la superficie gaussiana, la dirección es de $O$ a $P$, y para una carga neta negativa, la dirección es de $P$ a $O$. Esto es todo lo que necesitamos para una carga puntual, y notarás que el resultado anterior es idéntico al de una carga puntual.
Sin embargo, la ley de Gauss se vuelve realmente útil en casos donde la carga ocupa un volumen finito.
Calcular la carga encerrada
El caso más interesante es cuando una distribución de carga esférica ocupa un volumen y te preguntas qué campo eléctrico dentro de la distribución de carga se vuelve relevante. En este caso, la carga adjunta depende de la distancia r del punto del campo en relación con el radio de la distribución de carga $R$, tal como se muestra en la .
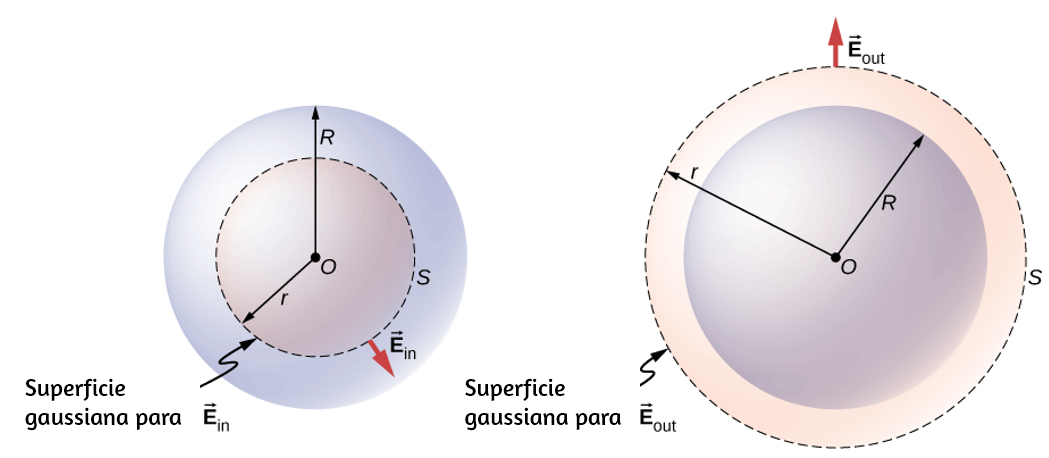
Si el punto $P$ está ubicado fuera de la distribución de carga, es decir, si $r≥R$, entonces la superficie gaussiana que contiene P encierra todas las cargas en la esfera. En este caso, $q_{\textsf{enc}}$ es igual a la carga total en la esfera. Por otro lado, si el punto $P$ está dentro de la distribución de carga esférica, es decir, si $r < R$, entonces la superficie gaussiana encierra una esfera más pequeña que la esfera de distribución de carga. En este caso, $q_{\textsf{enc}}$ es menor que la carga total presente en la esfera. Con referencia a la , podemos escribir $q_{\textsf{enc}}$ como
El campo en un punto fuera de la distribución de carga también se denomina $\overrightarrow{\bold{E}}_{\textsf{out}}$, y el campo en un punto dentro de la distribución de carga se llama $\overrightarrow{\bold{E}}_{\textsf{in}}$. Centrándose en los dos tipos de puntos de campo, dentro o fuera de la distribución de carga, ahora podemos escribir la magnitud del campo eléctrico como
$$P_{\textsf{fuera de la esfera}} E_{\textsf{out}} = \frac{1}{4πε_0} \frac{q_{\textsf{tot}}}{r^2} \tag{6.9}$$ $$P_{\textsf{dentro de la esfera}} E_{\textsf{in}} = \frac{1}{4πε_0} \frac{q_{\textsf{dentro de }r < R}}{r^2} \tag{6.10}$$Observa que el campo eléctrico fuera de una distribución de carga esféricamente simétrica es idéntico al de una carga puntual en el centro que tiene una carga igual a la carga total de la distribución de carga esférica. Esto es notable ya que las cargas no se encuentran solo en el centro. Ahora elaboramos ejemplos específicos de distribuciones esféricas de carga, comenzando con el caso de una esfera con carga uniforme.
Ejemplo 6.6
Esfera uniformemente cargada
Una esfera de radio $R$, como la que se muestra en la , tiene una densidad de carga de volumen uniforme $ρ_0$. Encuentra el campo eléctrico en un punto fuera de la esfera y en un punto dentro de la esfera.
Estrategia
Aplica la estrategia de resolución de problemas de la ley de Gauss, donde ya hemos resuelto el cálculo del flujo.
Solución
La carga encerrada por la superficie gaussiana viene dada por
$$q_{\textsf{enc}} = \int ρ_0dV = \int_0^{r} ρ_04πr'^2dr' = ρ_0 \left(\frac{4}{3}πr^3 \right)$$La respuesta para la amplitud del campo eléctrico se puede anotar inmediatamente para un punto fuera de la esfera, etiquetado como $E_{\textsf{out}}$, y un punto dentro de la esfera, etiquetado como $E_{\textsf{out}}$.
$$E_{\textsf{out}} = \frac{1}{4πε_0}\frac{q_{\textsf{tot}}}{r^2}, q_{\textsf{tot}} = \frac{4}{3}πR^3ρ_0$$ $$E_{\textsf{in}} = \frac{q_{\textsf{enc}}}{4πε_0r^2} = \frac{ρ_0r}{3ε_0}, \, \textsf{ ya que } \, q_{\textsf{enc}} = \frac{4}{3}πr^3ρ_0$$Es interesante observar que la magnitud del campo eléctrico aumenta dentro del material a medida que sale, ya que la cantidad de carga encerrada por la superficie gaussiana aumenta con el volumen.
Específicamente, la carga encerrada crece $αr^3$, mientras que el campo de cada elemento infinitesimal de carga cae $a_1/r^2$ con el resultado neto de que el campo eléctrico dentro de la distribución aumenta en fuerza linealmente con el radio. La magnitud del campo eléctrico fuera de la esfera disminuye a medida que se aleja de las cargas, porque la carga incluida sigue siendo la misma pero la distancia aumenta. La muestra la variación de la magnitud del campo eléctrico con la distancia desde el centro de una esfera cargada uniformemente.
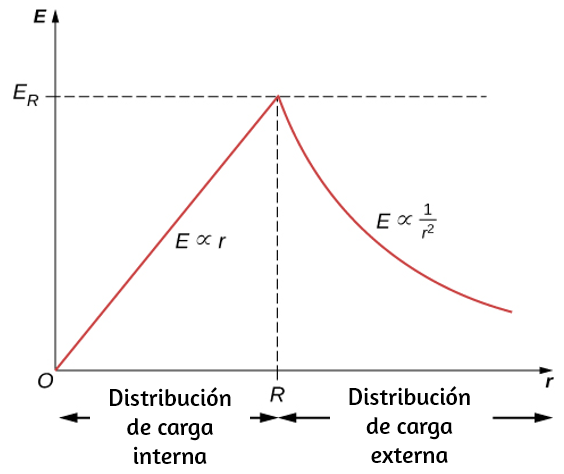
La dirección del campo eléctrico en cualquier punto $P$ está radialmente hacia afuera desde el origen si $ρ_0$ es positivo, y hacia adentro (es decir, hacia el centro) si $ρ_0$ es negativo. El campo eléctrico en algunos puntos espaciales representativos se muestra en la cuyas coordenadas radiales $r$ son $r = R/2$, $r = R$ y $r = 2R$.
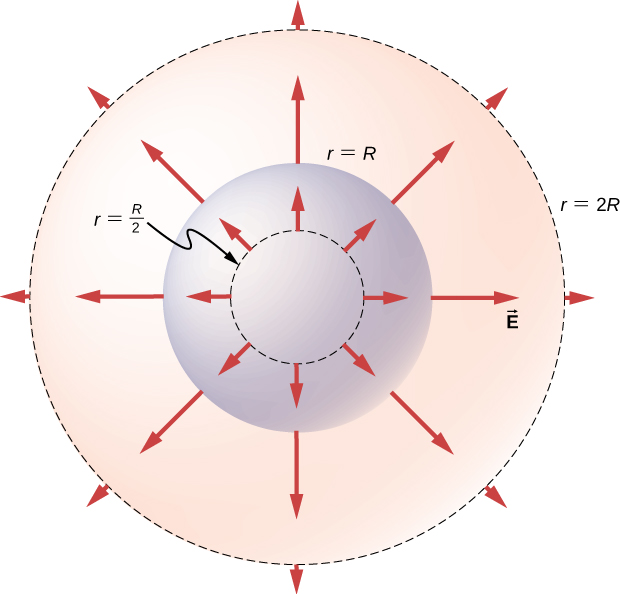
Explicación
Observa que $E_{\textsf{out}}$ tiene la misma forma que la ecuación del campo eléctrico de una carga puntual aislada. Al determinar el campo eléctrico de una distribución de carga esférica uniforme, podemos por lo tanto asumir que toda la carga dentro de la superficie gaussiana esférica apropiada se encuentra en el centro de la distribución.
Ejemplo 6.7
Esfera no uniformemente cargada
Una esfera no conductora de radio $R$ tiene una densidad de carga no uniforme que varía con la distancia desde su centro según lo dado por
$$ρ(r) = ar^n(r ≤ R; n ≥ 0),$$donde $a$ es una constante. Requerimos $n ≥ 0$ para que la densidad de carga no esté indefinida en $r = 0$. Encuentra el campo eléctrico en un punto fuera de la esfera y en un punto dentro de la esfera.
Estrategia
Aplica la estrategia de la ley de Gauss dada anteriormente, donde trabajamos las integrales de carga adjuntas por separado para casos dentro y fuera de la esfera.
Solución
Dado que la función de densidad de carga dada solo tiene una dependencia radial y no depende de la dirección, tenemos una situación esférica simétrica. Por lo tanto, la magnitud del campo eléctrico en cualquier punto se da arriba y la dirección es radial. Solo necesitamos encontrar la carga adjunta $q_{\textsf{enc}}$, que depende de la ubicación del punto del campo.
Una nota sobre los símbolos: usamos $r'$ para ubicar cargas en la distribución de carga y $r$ para ubicar los puntos de campo en la(s) superficie(s) gaussiana(s). La letra $R$ se usa para el radio de la distribución de carga.
Como la densidad de carga no es constante aquí, necesitamos integrar la función de densidad de carga sobre el volumen encerrado por la superficie gaussiana. Por lo tanto, configuramos el problema para las cargas en un caparazón esférico, digamos entre $r'$ y $r' + dr'$, como se muestra en la . El volumen de cargas en el caparazón de ancho infinitesimal es igual al producto del área de superficie $4πr'^2$ y el grosor $dr'$. Multiplicando el volumen con la densidad en esta ubicación, que es $ar'^n$, da la carga en el caparazón:
$$dq = ar'^n4πr'^2dr'$$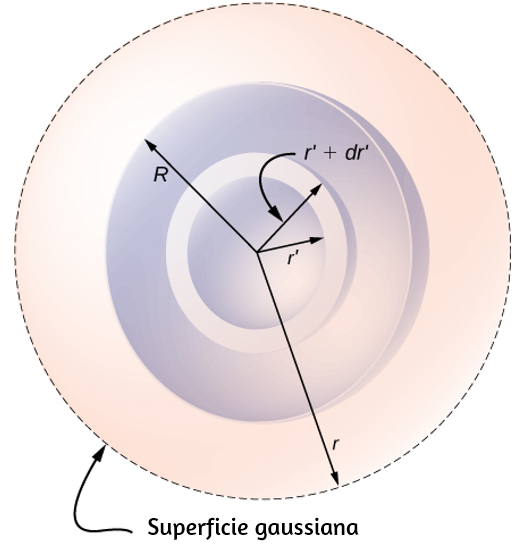
(a) Campo en un punto fuera de la distribución de carga. En este caso, la superficie gaussiana, que contiene el punto de campo $P$, tiene un radio $r$ que es mayor que el radio $R$ de la distribución de carga, $r > R$. Por lo tanto, todas las cargas de la distribución de carga están encerradas dentro de la superficie de Gauss.
Ten en cuenta que el espacio entre $r' = R$ y $r' = r$ está vacío de cargas y, por lo tanto, no contribuye a la integral sobre el volumen encerrado por la superficie Gaussiana:
$$q_{\textsf{enc}} = \int ρ_0dq = \int_0^{R} ar'^n4πr'^2dr' = \frac{4πa}{n + 3}R^{n+3}$$Esto se usa en el resultado general para el $\overrightarrow{\bold{E}}_{\textsf{out}}$ de arriba para obtener el campo eléctrico en un punto fuera de la distribución de carga como
$$\overrightarrow{\bold{E}}_{\textsf{out}} = [\frac{aR^{n+3}}{ε_0(n + 3)}]\frac{1}{r^2}\^{r}$$donde $\^{r}$ es un vector unitario en la dirección desde el origen hasta el punto del campo en la superficie gaussiana.
(b) Campo en un punto dentro de la distribución de carga. La superficie Gaussiana ahora está enterrada dentro de la distribución de carga, con $r < R$. Por lo tanto, solo las cargas en la distribución que están dentro de una distancia r del centro de la distribución de carga esférica cuentan en $r_{\textsf{enc}}$:
$$q_{\textsf{enc}} = \int_0^{r} ar'^n4πr'^2dr' = \frac{4πa}{n + 3}r^{n+3}$$Ahora, usando el resultado general anterior para $\overrightarrow{\bold{E}}_{\textsf{in}}$, encontramos el campo eléctrico en un punto que está a una distancia r del centro y se encuentra dentro de la distribución de carga como
$$\overrightarrow{\bold{E}}_{\textsf{in}} = \left[\frac{a}{ε_0(n + 3)} \right]r^{n + 1}\^{r}$$donde se incluye la información de la dirección usando el vector radial de la unidad.
 Comprueba tu aprendizaje 6.4
Comprueba tu aprendizaje 6.4
Una distribución de carga tiene simetría cilíndrica si la densidad de carga depende únicamente de la distancia $r$ desde el eje de un cilindro y no debe variar a lo largo del eje o con una dirección alrededor del eje. En otras palabras, si su sistema varía si lo gira alrededor del eje o lo desplaza a lo largo del eje, no tiene simetría cilíndrica.
La muestra cuatro situaciones en las que las cargas se distribuyen en un cilindro. Una densidad de carga uniforme $ρ_0$ en un cable recto infinito tiene una simetría cilíndrica, y también lo hace un cilindro infinitamente largo con densidad de carga constante $ρ_0$. Un cilindro infinitamente largo que tiene diferentes densidades de carga a lo largo de su longitud, como una densidad de carga $ρ_1$ para $z > 0$ y $ρ_0 ≠ ρ_1$ para $z < 0$, no tiene una simetría cilíndrica útil para este curso.
Tampoco lo hace un cilindro en el que la densidad de carga varía con la dirección, como una densidad de carga $ρ_1$ para $0 ≤ θ ≤ π$ y $ρ_2 ≠ ρ_1$ para $π ≤ θ ≤ 2π$. Un sistema con conchas cilíndricas concéntricas, cada una con densidades de carga uniformes, aunque diferentes en diferentes capas, como en la figura (d), tiene simetría cilíndrica si son infinitamente largas.
El requisito de longitud infinita se debe a que la densidad de carga cambia a lo largo del eje de un cilindro finito. En sistemas reales, no tenemos infinitos cilindros; sin embargo, si el objeto cilíndrico es considerablemente más largo que el radio del que estamos interesados, entonces la aproximación de un cilindro infinito se vuelve útil.
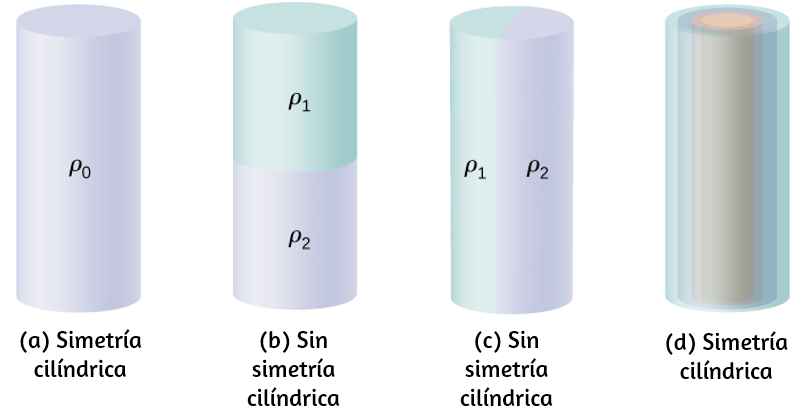
Consecuencias de la simetría
En todos los casos de simetría cilíndrica, el campo eléctrico $\overrightarrow{\bold{E}}_P$ en cualquier punto $P$ también debe mostrar simetría cilíndrica.
$$\textsf{Simetría cilíndrica}: \overrightarrow{\bold{E}}_P = E_P(r)\^{r}$$donde $r$ es la distancia desde el eje y $r$ es un vector unitario dirigido perpendicularmente desde el eje ().
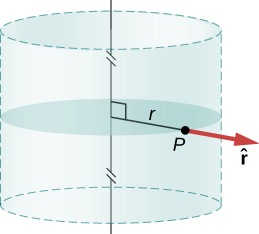
Cálculo Gaussiano de superficie y flujo
Para utilizar la dirección y la dependencia funcional del campo eléctrico, elegimos una superficie gaussiana cerrada en forma de cilindro con el mismo eje que el eje de la distribución de carga.
El flujo a través de esta superficie de radio y altura L es fácil de calcular si dividimos nuestra tarea en dos partes: (a) un flujo a través de los extremos planos y (b) un flujo a través de la superficie curva ().
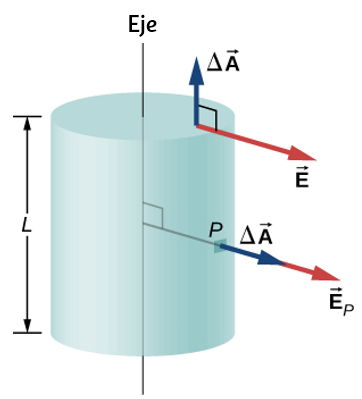
El campo eléctrico es perpendicular al lado cilíndrico y paralelo a las tapas terminales planas de la superficie. El flujo a través de la parte cilíndrica es
mientras que el flujo a través de las tapas finales es cero porque $\overrightarrow{\bold{E}} \cdot \^{n} = 0$ allí. Por lo tanto, el flujo es
$$\int_S \overrightarrow{\bold{E}} \cdot \^{r}dA = E(2πL) + 0 + 0 = 2πrLE$$Usando la ley de Gauss
De acuerdo con la ley de Gauss, el flujo debe ser igual a la cantidad de carga dentro del volumen encerrado por esta superficie, dividido por la permitividad del espacio libre. Cuando haces el cálculo para un cilindro de longitud $L$, encuentras que la $q_{\textsf{enc}}$ de la ley de Gauss es directamente proporcional a $L$. Escribámoslo como carga por unidad de longitud ($λ_{\textsf{enc}}$) por longitud $L$:
$$q_{\textsf{enc}} = λ_{\textsf{enc}}L$$Por lo tanto, la ley de Gauss para cualquier distribución de carga simétrica cilíndrica produce la siguiente magnitud del campo eléctrico a una distancia s lejos del eje:
$$\textsf{Magnitud}: E(r) = \frac{λ_{\textsf{enc}}}{2πε_0}\frac{1}{r}$$La carga por unidad de longitud $λ_{\textsf{enc}}$ depende de si el punto de campo está dentro o fuera del cilindro de distribución de carga, tal como lo hemos visto para la distribución esférica.
Calcular la carga encerrada
Sea $R$ el radio del cilindro dentro del cual las cargas se distribuyen de forma cilíndricamente simétrica. Toma el punto $P$ del campo a una distancia $s$ del eje (el lado de la superficie gaussiana incluye el punto de campo $P$). Cuando $r > R$ (es decir, cuando $P$ está fuera de la distribución de carga), la superficie gaussiana incluye toda la carga en el cilindro de radio $R$ y longitud $L$. Cuando $r < R$ ($P$ está ubicado dentro de la distribución de carga), entonces solo la carga dentro de un cilindro de radio $s$ y longitud $L$ está encerrada por la superficie gaussiana:
$$λ_{\textsf{enc}} = \begin{cases} \textsf{(carga total) } \; r \geq R \\ \textsf{(caga con } r < R\textsf{) si } r < R \end{cases}$$Ejemplo 6.8
Carcasa cilíndrica con carga uniforme
Una carcasa cilíndrica no conductora muy larga de radio $R$ tiene una densidad de carga superficial uniforme $σ_0$. Encuentra el campo eléctrico (a) en un punto fuera del caparazón y (b) en un punto dentro del caparazón.
Estrategia
Aplica la estrategia de ley de Gauss dada anteriormente, donde tratamos los casos dentro y fuera del caparazón por separado.
Solución
a. Campo eléctrico en un punto fuera del caparazón. Para un punto fuera de la carcasa cilíndrica, la superficie gaussiana es la superficie de un cilindro de radio $r > R$ y longitud $L$, como se muestra en la . La carga encerrada por el cilindro gaussiano es igual a la carga en la envuelta cilíndrica de longitud $L$. Por lo tanto, $λ_{\textsf{enc}}$ está dada por
$$λ_{\textsf{enc}} = \frac{σ_02πRL}{L} = 2πRσ_0$$
Por lo tanto, el campo eléctrico en un punto $P$ fuera de la carcasa a una distancia $r$ lejos del eje es
donde $r$ es un vector unitario, perpendicular al eje y apuntando hacia afuera, como se muestra en la figura. El campo eléctrico en $P$ apunta en la dirección de $r$ dada en la si $σ_0 > 0$ y en la dirección opuesta a $r$ si $σ_0 < 0$.
b. Campo eléctrico en un punto dentro del caparazón. Para un punto dentro de la capa cilíndrica, la superficie Gaussiana es un cilindro cuyo radio $r$ es menor que $R$ (). Esto significa que no se incluyen cargas dentro de la superficie de Gauss: $λ_{\textsf{enc}} = 0$.
Esto da la siguiente ecuación para la magnitud del campo eléctrico $E_{\textsf{in}}$ en un punto cuya $r$ es menor que $R$ del caparazón de las cargas.
$$E_{\textsf{in}}2πrL = 0(r < R),$$Esto nos da
$$E_{\textsf{in}} = 0(r < R)$$Explicación
Ten en cuenta que el resultado dentro del caparazón es exactamente lo que deberíamos esperar: sin carga cerrada significa cero campo eléctrico. Fuera del caparazón, el resultado se vuelve idéntico a un cable con carga uniforme $Rσ_0$.
 Comprueba tu aprendizaje 6.5
Comprueba tu aprendizaje 6.5
Se obtiene una simetría plana de densidad de carga cuando las cargas se distribuyen uniformemente sobre una gran superficie plana. En la simetría plana, todos los puntos en un plano paralelo al plano de carga son idénticos con respecto a las cargas.
Consecuencias de la simetría
Tomamos el plano de la distribución de carga para que sea el plano $xy$ y encontramos el campo eléctrico en un punto espacial $P$ con coordenadas $(x, y, z)$. Dado que la densidad de carga es la misma para todas las coordenadas $(x, y)$ en el plano $z = 0$, por simetría, el campo eléctrico en $P$ no puede depender de las coordenadas $x$ o $y$ del punto $P$, como se muestra en la . Por lo tanto, el campo eléctrico en $P$ solo puede depender de la distancia desde el plano y tiene una dirección ya sea hacia el plano o lejos del plano. Es decir, el campo eléctrico en $P$ tiene solo un componente $z$ distinto de cero.
Cargas uniformes en el plano $xy: \overrightarrow{\bold{E}}= E(z)\^{z}$
donde $z$ es la distancia desde el plano y $\^{z}$ es el vector unitario normal al plano. Ten en cuenta que en este sistema, $E(z) = E(-z)$, aunque, por supuesto, apuntan en direcciones opuestas.
Cálculo Gaussiano de superficie y flujo
En el presente caso, una superficie Gaussiana conveniente es una caja, ya que el campo eléctrico esperado apunta en una sola dirección. Para mantener la caja gaussiana simétrica sobre el plano de cargas, la llevamos a horcajadas sobre el plano de las cargas, de modo que una cara que contiene el punto $P$ del campo se toma paralela al plano de las cargas. En la , los lados I y II de la superficie Gaussiana (la caja) que son paralelos al plano infinito han sido sombreados. Son las únicas superficies que dan lugar a flujo distinto de cero porque el campo eléctrico y los vectores de área de las otras caras son perpendiculares entre sí.
Sea $A$ el área de la superficie sombreada en cada lado del plano y $E_P$ la magnitud del campo eléctrico en el punto $P$. Dado que los lados I y II están a la misma distancia del plano, el campo eléctrico tiene la misma magnitud en puntos en estos planos, aunque las direcciones del campo eléctrico en estos puntos en los dos planos son opuestas entre sí.
$$\textsf{Magnitud en I o II}: E(z) = E_P$$Si la carga en el plano es positiva, entonces la dirección del campo eléctrico y los vectores de área son como se muestra en la . Por lo tanto, encontramos para el flujo de campo eléctrico a través de la caja
$$\begin{align*} Φ &= \oint_S \overrightarrow{\bold{E}}_P \cdot \^{n}d A \\ &= E_PA + E_PA + 0 + 0 + 0 + 0 = 2E_PA \tag{6.11} \end{align*}$$donde los ceros son para el flujo a través de los otros lados de la caja. Observa que si la carga en el plano es negativa, las direcciones del campo eléctrico y los vectores de área para los planos I y II son opuestas entre sí, y obtenemos un signo negativo del flujo. De acuerdo con la ley de Gauss, el flujo debe ser igual a $q_{\textsf{enc}}/ε_0$. En la , vemos que las cargas dentro del volumen encerrado por la caja gaussiana residen en un área $A$ del plano $xy$. Por lo tanto,
$$q_{\textsf{enc}} = σ_0A \tag{6.12}$$Usando las ecuaciones para el flujo y la carga encerrada en la ley de Gauss, podemos determinar inmediatamente el campo eléctrico en un punto a una altura z desde un plano cargado uniformemente en el plano $xy$:
$$\overrightarrow{\bold{E}}_P = \frac{σ_0}{2ε_0}\^{n}$$La dirección del campo depende del signo de la carga en el plano y del lado del plano donde se encuentra el punto $P$ del campo. Observa que encima del plano, $\^{n} = + \^{z}$, mientras que debajo del plano, $\^{n} = -\^{z}$.
Puede sorprenderte al notar que el campo eléctrico en realidad no depende de la distancia desde el plano; este es un efecto de la suposición de que el plano es infinito. En términos prácticos, el resultado dado anteriormente sigue siendo una aproximación útil para planos finitos cerca del centro.
Hasta ahora, generalmente hemos estado trabajando con cargas que ocupan un volumen dentro de un aislador. Ahora estudiaremos qué ocurre cuando se le ponen cargas libres a un conductor. Generalmente, en presencia de un campo eléctrico (generalmente externo), la carga libre en un conductor se redistribuye y alcanza rápidamente el equilibrio electrostático. La distribución de carga resultante y su campo eléctrico tienen muchas propiedades interesantes, que podemos investigar con la ayuda de la ley de Gauss y el concepto de potencial eléctrico.
Si un campo eléctrico está presente dentro de un conductor, ejerce fuerzas sobre los electrones libres (también llamados electrones de conducción), que son electrones en el material que no están unidos a un átomo. Estos electrones libres luego se aceleran. Sin embargo, mover cargas por definición significa condiciones no estáticas, contrariamente a nuestra suposición. Por lo tanto, cuando se alcanza el equilibrio electrostático, la carga se distribuye de tal forma que el campo eléctrico dentro del conductor desaparece.
Si colocas una pieza de metal cerca de una carga positiva, los electrones libres en el metal son atraídos por la carga positiva externa y migran libremente hacia esa región.
La región a la que se mueven los electrones tiene un exceso de electrones sobre los protones en los átomos y la región desde donde los electrones han migrado tiene más protones que electrones. En consecuencia, el metal desarrolla una región negativa cerca de la carga y una región positiva en el otro extremo (). Como vimos en el capítulo anterior, esta separación de igual magnitud y tipo opuesto de carga eléctrica se llama polarización. Si quitas la carga externa, los electrones migrarán hacia atrás y neutralizarán la región positiva.
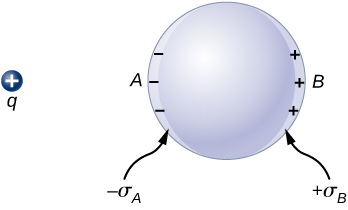
La polarización del metal ocurre solo en presencia de cargas externas. Puedes pensar en esto en términos de campos eléctricos. La carga externa crea un campo eléctrico externo. Cuando el metal se coloca en la región de este campo eléctrico, los electrones y protones del metal experimentan fuerzas eléctricas debido a este campo eléctrico externo, pero solo los electrones de conducción son libres de moverse en el metal sobre distancias macroscópicas.
El movimiento de los electrones de conducción conduce a la polarización, que crea un campo eléctrico inducido además del campo eléctrico externo ().
El campo eléctrico neto es una suma vectorial de los campos de $+q$ y las densidades de carga superficial $-σ_A$ y $+σ_B$. Esto significa que el campo dentro del conductor es diferente del campo fuera del conductor.
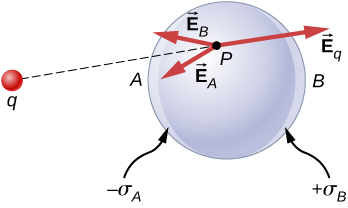
La redistribución de cargas es tal que la suma de las tres contribuciones en cualquier punto $P$ dentro del conductor es
$$\overrightarrow{\bold{E}}_P = \overrightarrow{\bold{E}}_q + \overrightarrow{\bold{E}}_B + \overrightarrow{\bold{E}}_A = \overrightarrow{0}.$$Ahora, gracias a la ley de Gauss, sabemos que no hay una carga neta encerrada por una superficie gaussiana que esté únicamente dentro del volumen del conductor en equilibrio. Es decir, $q_{\textsf{enc}} = 0$ y por lo tanto
Una propiedad interesante de un conductor en equilibrio estático es que las cargas adicionales en el conductor terminan en la superficie externa del conductor, independientemente de dónde se originan. La ilustra un sistema en el que llevamos una carga positiva externa dentro de la cavidad de un metal y luego la tocamos en la superficie interior. Inicialmente, la superficie interna de la cavidad está cargada negativamente y la superficie externa del conductor está cargada positivamente. Cuando tocamos la superficie interna de la cavidad, la carga inducida se neutraliza, dejando la superficie exterior y todo el metal cargados con una carga neta positiva.
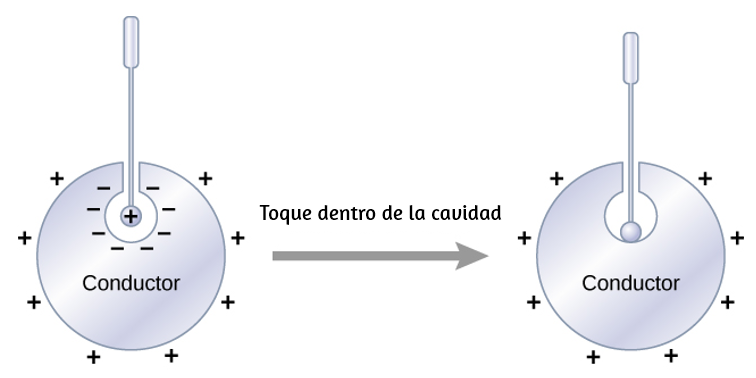
Para ver por qué sucede esto, ten en cuenta que la superficie gaussiana en la (la línea punteada) sigue el contorno de la superficie real del conductor y se encuentra a una distancia infinitesimal dentro de ella. Como $E = 0$ en todas partes dentro de un conductor,
$$\oint_S \overrightarrow{\bold{E}} \cdot \^{n}d A = 0$$Por lo tanto, según la ley de Gauss, no hay carga neta dentro de la superficie de Gauss. Pero la superficie gaussiana se encuentra justo debajo de la superficie real del conductor; en consecuencia, no hay carga neta dentro del conductor. Cualquier exceso de carga debe estar en su superficie.
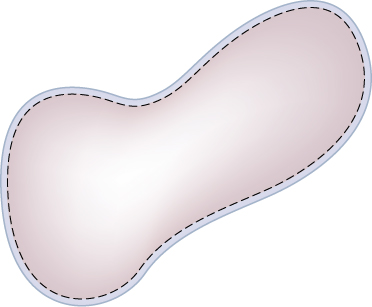
Esta propiedad particular de los conductores es la base de un método extremadamente preciso desarrollado por Plimpton y Lawton en 1936 para verificar la ley de Gauss y, en consecuencia, la ley de Coulomb. Un esquema de sus aparatos se muestra en la . Dos carcasas esféricas están conectadas entre sí a través de un electrómetro $E$, un dispositivo que puede detectar una pequeña cantidad de carga que fluye de un caparazón al otro. Cuando el interruptor $S$ se lanza hacia la izquierda, la batería $B$ coloca la carga en el caparazón exterior $B$. ¿Fluirá la carga a través del electrómetro hacia la carcasa interna?
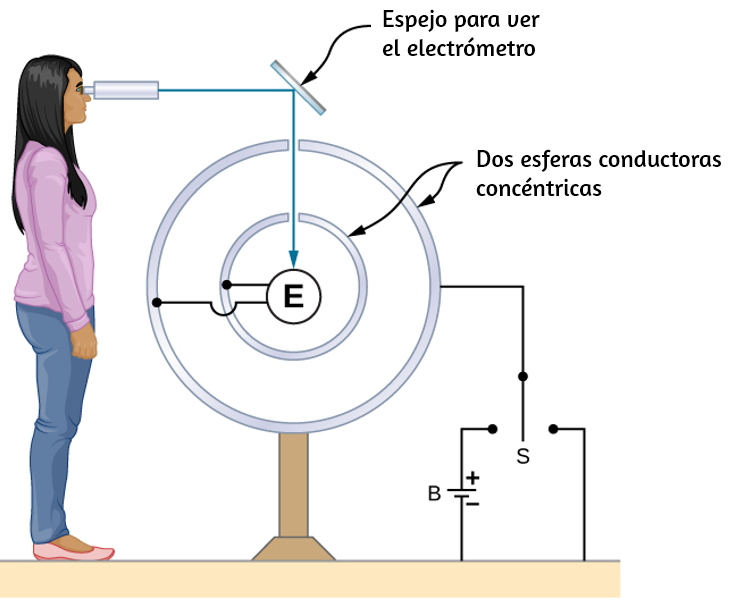
No. Hacerlo significaría una violación de la ley de Gauss. Plimpton y Lawton no detectaron ningún flujo y, conociendo la sensibilidad de su electrómetro, concluyeron que si la dependencia radial en la ley de Coulomb fuera $1/r^{(2 + Δ)}$, $Δ$ sería menor que $2 × 10^{-9}$. Mediciones más recientes colocan $Δ$ a menos de $3 × 10-^{-16}$, un número tan pequeño que la validez de la ley de Coulomb parece indiscutible.
Si el campo eléctrico tuviera un componente paralelo a la superficie de un conductor, las cargas libres en la superficie se moverían, una situación contraria al supuesto del equilibrio electrostático. Por lo tanto, el campo eléctrico es siempre perpendicular a la superficie de un conductor.
En cualquier punto justo por encima de la superficie de un conductor, la densidad de carga superficial $σ$ y la magnitud del campo eléctrico $E$ están relacionadas por
Para ver esto, considera un cilindro gaussiano infinitesimalmente pequeño que rodea un punto en la superficie del conductor, como en la . El cilindro tiene una cara del extremo adentro y una cara del extremo fuera de la superficie. La altura y el área de la sección transversal del cilindro son $Δ$ y $ΔA$, respectivamente. Los lados del cilindro son perpendiculares a la superficie del conductor, y sus caras finales son paralelas a la superficie. Debido a que el cilindro es infinitesimalmente pequeño, la densidad de carga $σ$ es esencialmente constante sobre la superficie encerrada,
por lo que la carga total dentro del cilindro gaussiano es $σΔA$. Ahora E es perpendicular a la superficie del conductor fuera del conductor y desaparece dentro de él, porque de lo contrario, las cargas se acelerarían, y no estaríamos en equilibrio. Por lo tanto, el flujo eléctrico cruza solo la cara del extremo exterior de la superficie gaussiana y puede escribirse como $EΔA$, ya que se supone que el cilindro es suficientemente pequeño para que $E$ sea aproximadamente constante sobre esa área. De la ley de Gauss,
$$EΔA = \frac{σΔA}{ε_0}.\textsf{ Entonces, }E = \frac{σ}{ε_0}$$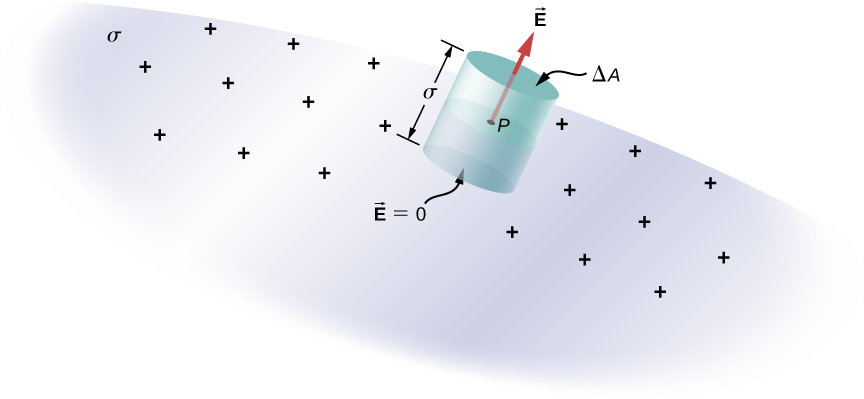
Ejemplo 6.9
Campo eléctrico de una placa conductora
La placa conductora infinita de la tiene una densidad de carga superficial uniforme $σ$. Usa la ley de Gauss para encontrar el campo eléctrico fuera de la placa. Compara este resultado con el calculado previamente directamente.
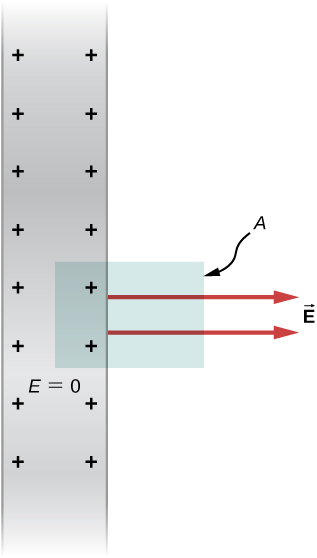
Estrategia
Para este caso, usamos una superficie gaussiana cilíndrica, una vista lateral de la cual se muestra.
Solución
El cálculo del flujo es similar al de una hoja infinita de carga del capítulo anterior con una excepción importante: la cara izquierda de la superficie gaussiana está dentro del conductor donde $\overrightarrow{\bold{E}} = \overrightarrow{0}$, por lo que el flujo total a través de la superficie gaussiana es $EA$ en lugar de $2EA$. Luego desde la ley de Gauss,
$$EA = \frac{σA}{ε_0}$$y el campo eléctrico fuera de la placa es
$$E = \frac{σ}{ε_0}$$Explicación
Este resultado está de acuerdo con el resultado de la sección anterior y es consistente con la regla establecida anteriormente.
Ejemplo 6.10
Campo eléctrico entre placas paralelas con cargas opuestas
Dos grandes placas conductoras tienen cargas iguales y opuestas, con una densidad de carga superficial $σ$ de magnitud $6,81 × 10^{-7} C/m^2$, como se muestra en la . La separación entre las placas es $l = 6,50 mm$. ¿Cuál es el campo eléctrico entre las placas?
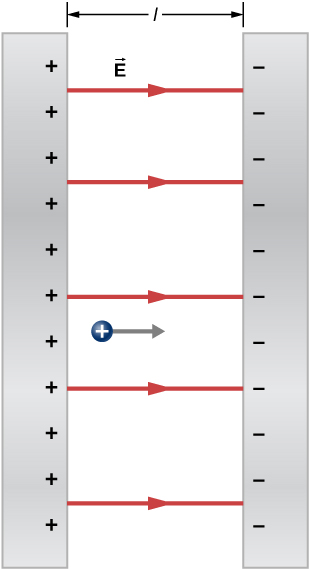
Estrategia
Observa que el campo eléctrico en la superficie de una placa solo depende de la carga en esa placa. Por lo tanto, aplica $E = σ/ε_0$ con los valores dados.
Solución
El campo eléctrico se dirige desde la placa positiva a la negativa, como se muestra en la figura, y su magnitud viene dada por
$$E = \frac{σ}{ε_0} = \frac{6.81 × 10^{−7} C/m^2}{8.85 × 10^{−12} C^2/N m^2} = 7.69 × 10^4 N/C$$Explicación
Esta fórmula es aplicable a más que solo una placa. Además, los sistemas de dos placas serán importantes más adelante.
Ejemplo 6.11
Una Esfera conductora
La esfera conductora aislada () tiene un radio $R$ y una carga excedente $q$. ¿Cuál es el campo eléctrico tanto dentro como fuera de la esfera?
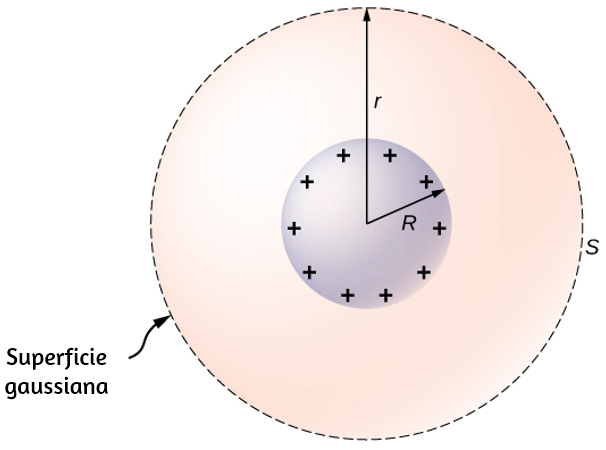
Estrategia
La esfera está aislada, por lo que su distribución de cambio de superficie y el campo eléctrico de esa distribución son esféricamente simétricos. Por lo tanto, podemos representar el campo como $\overrightarrow{\bold{E}} = E(r)\^{r}$. Para calcular $E(r)$, aplicamos la ley de Gauss sobre una superficie esférica cerrada $S$ de radio $r$ que es concéntrica con la esfera conductora.
Solución
Como $r$ es constante y $\^{n} = \^{r}$ en la esfera,
$$\oint_S \overrightarrow{\bold{E}} \cdot \^{n}d A = E(r)\oint_S d A = E(r)4πr^2$$Para $r < R$, $S$ está dentro del conductor, entonces $q_{\textsf{enc}} = 0$, y la ley de Gauss arroja:
$$E(r) = 0$$como se esperaba dentro de un conductor. Si $r > R$, $S$ encierra el conductor de modo que $q_{\textsf{enc}} = q$. De la ley de Gauss,
$$E(r)4πr^2 = \frac{q}{ε_0}$$El campo eléctrico de la esfera, por lo tanto, puede escribirse como
$$\overrightarrow{\bold{E}} = 0, (r < R)$$ $$\overrightarrow{\bold{E}} = \frac{1}{4πε_0}\frac{q}{r^2}\^{r}, (r > R)$$Explicación
Observa que en la región $r ≥ R$, el campo eléctrico debido a una carga $q$ colocada en una esfera conductora aislada de radio $R$ es idéntico al campo eléctrico de una carga puntual $q$ situada en el centro de la esfera. La diferencia entre el metal cargado y una carga puntual ocurre solo en los puntos del espacio dentro del conductor.
Para una carga puntual colocada en el centro de la esfera, el campo eléctrico no es cero en los puntos del espacio ocupados por la esfera, pero un conductor con la misma cantidad de carga tiene un campo eléctrico cero en esos puntos (). Sin embargo, no hay distinción en los puntos exteriores en el espacio donde $r > R$, y podemos reemplazar el conductor esférico cargado aislado por una carga puntual en su centro con impunidad.
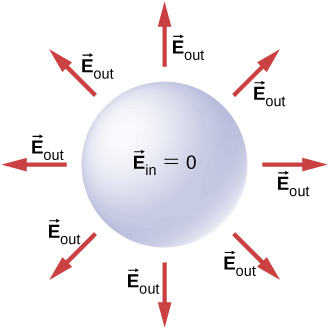
 Comprueba tu aprendizaje 6.6
Comprueba tu aprendizaje 6.6
Para un conductor con una cavidad, si ponemos una carga $+q$ dentro de la cavidad, entonces la separación de carga tiene lugar en el conductor, con una cantidad de carga $-q$ en la superficie interna y una cantidad de carga $+q$ en la superficie exterior ( (a)). Para el mismo conductor con una carga $+q$ fuera de él, no hay un exceso de carga en la superficie interior; tanto las cargas inducidas positivas como negativas residen en la superficie exterior ( (b)).
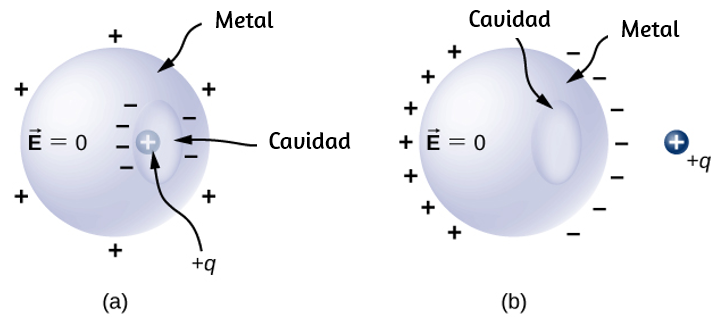
Si un conductor tiene dos cavidades, una de ellas tiene una carga $+q_a$ dentro y la otra una carga $-q_b$, la polarización del conductor da como resultado $-q_a$ en la superficie interior de la cavidad $a$, $+ q_b$ en la superficie interior de la cavidad $b$ y $q_a - q_b$ en la superficie exterior (). Las cargas en las superficies pueden no estar distribuidas uniformemente; su propagación depende de la geometría. La única regla obedecida es que cuando se ha alcanzado el equilibrio, la distribución de carga en un conductor es tal que el campo eléctrico por la distribución de carga en el conductor cancela el campo eléctrico de las cargas externas en todos los puntos espaciales dentro del cuerpo del conductor.
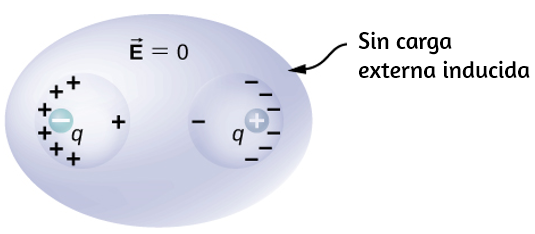
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, puedes investigar las implicaciones de la Ley de Gauss aplicada a esferas cargadas hechas de material conductivo. Puedes usar un caparazón esférico de paredes delgadas y/o un caparazón de paredes gruesas. Compara los campos obtenidos con el campo eléctrico de una carga puntual. La vista que se muestra en la escena representa un corte bidimensional en el centro de las esferas, por lo que se ven como círculos (la escena se diseñó a partir de una simulación del repositorio: http://online.scuola.zanichelli.it/fisica-files/).

Dos términos comúnmente utilizados para describir la electricidad son su energía y voltaje, que mostraremos en este capítulo y que está directamente relacionado con la energía potencial en un sistema. Sabemos, por ejemplo, que grandes cantidades de energía eléctrica se pueden almacenar en baterías, se transmiten a través del país a través de corrientes a través de líneas eléctricas y pueden saltar de las nubes para hacer estallar la savia de los árboles. De manera similar, a nivel molecular, los iones cruzan membranas celulares y la información de transferencia.
También sabemos sobre los voltajes asociados con la electricidad. Las baterías suelen tener unos pocos voltios, las salidas en tu hogar producen con frecuencia $120$ voltios, y las líneas de alimentación pueden llegar a cientos de miles de voltios. Pero la energía y el voltaje no son lo mismo.
Una batería de motocicleta, por ejemplo, es pequeña y no tendrías mucho éxito en reemplazarla por una batería de automóvil mucho más grande, pero cada una tiene el mismo voltaje. En este capítulo, examinaremos la relación entre el voltaje y la energía eléctrica, y comenzamos a explorar algunas de las muchas aplicaciones de la electricidad.
Cuando una carga positiva libre q es acelerada por un campo eléctrico, recibe energía cinética (). El proceso es análogo a un objeto acelerado por un campo gravitatorio, como si la carga descendiera por una colina eléctrica donde su energía potencial eléctrica se convierte en energía cinética, aunque, por supuesto, las fuentes de las fuerzas son muy diferentes. Exploremos el trabajo realizado en una carga q por el campo eléctrico en este proceso, de modo que podamos desarrollar una definición de energía potencial eléctrica.
La fuerza electrostática o Coulomb es conservadora, lo que significa que el trabajo realizado en q es independiente del camino tomado, como demostraremos más adelante. Esto es exactamente análogo a la fuerza gravitacional. Cuando una fuerza es conservadora, es posible definir una energía potencial asociada con la fuerza. Por lo general, es más fácil trabajar con la energía potencial (porque depende únicamente de la posición) que calcular el trabajo directamente.
Para mostrar esto explícitamente, considera una carga eléctrica $+ q$ fija en el origen y mueva otra carga $+ Q$ hacia q de tal manera que, en cada instante, la fuerza aplicada $\overrightarrow{\bold{F}}$ equilibre exactamente la fuerza eléctrica $\overrightarrow{\bold{F}}_e$ en $Q$ ().
El trabajo realizado por la fuerza aplicada $\overrightarrow{\bold{F}}$ sobre la carga $Q$ cambia la energía potencial de $Q$. Llamamos a esta energía potencial la energía potencial eléctrica de $Q$.
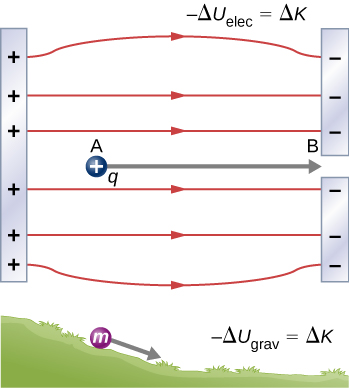
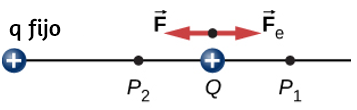
El trabajo $W_{12}$ realizado por la fuerza aplicada $\overrightarrow{\bold{F}}$ cuando la partícula se mueve de $P_1$ a $P_2$ se puede calcular mediante
$$W_{12} = \int_{P_1}^{P_2} \overrightarrow{\bold{F}} \cdot d\overrightarrow{\bold{l}}$$Dado que la fuerza aplicada $\overrightarrow{\bold{F}}$ equilibra la fuerza eléctrica $\overrightarrow{\bold{F}}_e$ en $Q$, las dos fuerzas tienen la misma magnitud y direcciones opuestas. Por lo tanto, la fuerza aplicada es
$$\overrightarrow{\bold{F}} = -\overrightarrow{\bold{F}}_e = -\frac{kqQ}{r^2}\^{r}$$donde hemos definido positivo en dirección lejos del origen y $r$ es la distancia desde el origen. Las direcciones tanto del desplazamiento como de la fuerza aplicada en el sistema de la son paralelas y, por lo tanto, el trabajo realizado en el sistema es positivo.
Usamos la letra $U$ para denotar la energía potencial eléctrica, que tiene unidades de julios ($J$). Cuando una fuerza conservadora hace un trabajo negativo, el sistema gana energía potencial. Cuando una fuerza conservadora hace un trabajo positivo, el sistema pierde energía potencial, $ΔU = -W$.
En el sistema de la , la fuerza de Coulomb actúa en la dirección opuesta al desplazamiento; por lo tanto, el trabajo es negativo. Sin embargo, hemos aumentado la energía potencial en el sistema de dos cargas.
Ejemplo 7.1
Energía cinética de una partícula cargada
Una carga $Q$ de $+ 3.0 nC $está inicialmente en reposo a una distancia de $10 cm$ ($r_1$) de una carga $q$ fija de $+ 5.0 nC$ en el origen (). Naturalmente, la fuerza de Coulomb acelera $Q$ lejos de $q$, llegando finalmente a $15 cm$ ($r_1$).
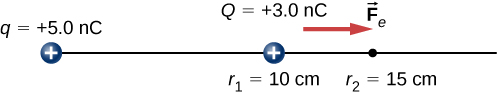
a. ¿Cuál es el trabajo realizado por el campo eléctrico entre $r_1$ y $r_2$?
b. ¿Cuánta energía cinética tiene $Q$ en $r_2$?
Estrategia
Calcula el trabajo con la definición usual. Como $Q$ comenzó desde el reposo, esto es lo mismo que la energía cinética.
Solución
Integrando la fuerza sobre la distancia, obtenemos
$$\begin{align*} W_{12} &= \int_{r_1}^{r_2} \overrightarrow{\bold{F}} \cdot d\overrightarrow{\bold{r}} = \int_{r_1}^{r_2} \frac{kqQ}{r^2}dr = kqQ \left[-\frac{1}{r_2} + \frac{1}{r_1} \right] \\ &= {\scriptsize (8.99 × 10^9 Nm^2/C^2)(5.0 × 10^{- 9}C)(3.0 × 10^{-9} C) \left[-\frac{1}{0.15 m} + \frac{1}{0.10 m}\right]} \\ &= 4.5 × 10^{-7} J \end{align*}$$Este es también el valor de la energía cinética en $r_2$.
Explicación
La carga $Q$ estaba inicialmente en reposo; el campo eléctrico de $q$ funcionó en $Q$, entonces ahora $Q$ tiene energía cinética igual al trabajo hecho por el campo eléctrico.
 Comprueba tu aprendizaje 7.1
Comprueba tu aprendizaje 7.1
En este ejemplo, el trabajo $W$ hecho para acelerar una carga positiva desde el reposo es positivo y resulta de una pérdida en $U$ o una $ΔU$ negativa. Se puede encontrar un valor para $U$ en cualquier punto tomando un punto como referencia y calculando el trabajo necesario para mover una carga al otro punto.
Energia potencial electrica
El trabajo $W$ para acelerar una carga positiva desde el reposo es positivo y resulta de una pérdida en $U$ o una $ΔU$ negativa. Matemáticamente,
$$W = -ΔU \tag{7.1}$$En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, desplaza la carga $Q$ y observa los valores que se obtienen para $ΔU$. También puedes cambiar los valores de las cargas $q$ y $Q$.
La energía potencial gravitacional y la energía potencial eléctrica son bastante análogas. La evaluación de la energía potencial para el trabajo realizado por una fuerza conservadora da una visión adicional con respecto a la energía y la transformación de energía sin la necesidad de lidiar con la fuerza directamente. Es mucho más común, por ejemplo, usar el concepto de energía potencial eléctrica que lidiar directamente con la fuerza de Coulomb en aplicaciones del mundo real. En coordenadas polares con $q$ en el origen y $Q$ ubicado en $r$, el vector del elemento de desplazamiento es $\overrightarrow{\bold{d}} = rdr$ y así el trabajo se convierte en
$$W_{12} = -kqQ = \int_{r_1}^{r_2} \overrightarrow{\bold{F}} \cdot d\overrightarrow{\bold{r}} = \int_{r_1}^{r_2} \frac{1}{r^2}\^{r} \cdot \^{r}dr = kqQ\frac{1}{r_2} - kqQ\frac{1}{r_1}$$Observa que este resultado solo depende de los puntos finales y es independiente de la ruta tomada. Para explorar esto más a fondo, compara la ruta $P_1$ a $P_2$ con la ruta $P_1P_3P_4P_2$ en la .
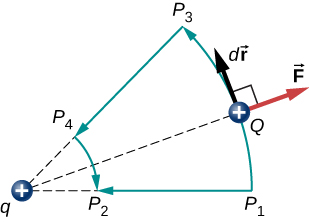
Los segmentos $P_1P_3$ y $P_4P_2$ son arcos de círculos centrados en $q$. Dado que la fuerza en $Q$ apunta hacia o desde $q$, no se realiza trabajo por una fuerza que equilibra la fuerza eléctrica, porque es perpendicular al desplazamiento a lo largo de estos arcos. Por lo tanto, el único trabajo realizado es a lo largo del segmento $P_3P_4$, que es idéntico a $P_1P_2$.
Una consecuencia de este cálculo de trabajo es que si tuviéramos que ir por el camino $P_1P_3P_4P_2P_1$, el trabajo neto sería cero (). Recuerda que así es como determinamos si una fuerza es conservadora o no. Por lo tanto, debido a que la fuerza eléctrica está relacionada con el campo eléctrico mediante $\overrightarrow{\bold{F}} = q\overrightarrow{\bold{E}}$, el campo eléctrico es en sí mismo conservador. Es decir,
$$\oint \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}} = 0$$Ten en cuenta que $Q$ es una constante.
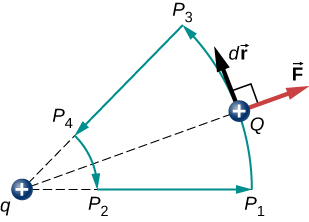
Otra implicación es que podemos definir una energía potencial eléctrica. Recuerda que el trabajo realizado por una fuerza conservadora también se expresa como la diferencia en la energía potencial correspondiente a esa fuerza. Por lo tanto, el trabajo $W_{\textsf{ref}}$ para traer una carga de un punto de referencia a un punto de interés se puede escribir como
$$W_{\textsf{ref}} = \int_{r_{\textsf{ref}}}^{r} \overrightarrow{\bold{F}} \cdot d\overrightarrow{\bold{l}}$$y, según la Ecuación 7.1, la diferencia en energía potencial ($U_2 - U_1$) de la carga de prueba $Q$ entre los dos puntos es
$$ΔU = - \int_{r_{\textsf{ref}}}^{r} \overrightarrow{\bold{F}} \cdot d\overrightarrow{\bold{l}}$$Por lo tanto, podemos escribir una expresión general para la energía potencial de dos cargas puntuales (en coordenadas esféricas):
$$ΔU = - \int_{r_{\textsf{ref}}}^{r} \frac{kqQ}{r^2}dr = kqQ \left[\frac{1}{r} - \frac{1}{r_{\textsf{ref}}} \right]$$Podemos tomar el segundo término como un nivel de referencia constante arbitrario, que sirve como referencia cero:
$$U(r) = k\frac{qQ}{r} - U_{\textsf{ref}}$$Una elección conveniente de referencia que se basa en nuestro sentido común es que cuando las dos cargas están infinitamente separadas, no hay interacción entre ellas (recuerda la discusión sobre la energía potencial de referencia en Energía potencial y Conservación de energía).
Tomando la energía potencial de este estado como cero se elimina el término $U_{\textsf{ref}}$ de la ecuación (como cuando decimos que el suelo es cero energía potencial en un potencial gravitatorio), y la energía potencial de $Q$ cuando está separada de q por una distancia $r$ asume la forma
Esta fórmula es simétrica con respecto a $q$ y $Q$, por lo que se describe mejor como la energía potencial del sistema de dos cargas.
Ejemplo 7.2
Energía potencial de una partícula cargada
Una carga $Q$ de $+ 3.0 nC$ está inicialmente en reposo a una distancia de $10 cm$ ($r_1$) de una carga $q$ fija de $+ 5.0 nC$ en el origen (). Naturalmente, la fuerza de Coulomb acelera $Q$ lejos de $q$, llegando finalmente a $15 cm$ ($r_1$).
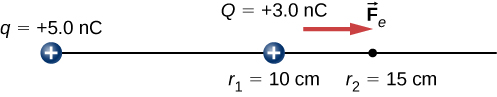
¿Cuál es el cambio en la energía potencial del sistema de dos cargas de $r_1$ a $r_1$?
Estrategia
Calcula la energía potencial con la definición dada anteriormente: $U_{12} = \int_{r_1}^{r_2} \overrightarrow{\bold{F}} \cdot d\overrightarrow{\bold{r}}$. Como $Q$ comenzó desde el reposo, esto es lo mismo que la energía cinética.
Solución
Tenemos
$$\begin{align*} U_{12} &= - \int_{r_1}^{r_2} \overrightarrow{\bold{F}} \cdot d\overrightarrow{\bold{r}} = - \int_{r_1}^{r_2} \frac{kqQ}{r^2}dr = kqQ \left[\frac{1}{r_2} - \frac{1}{r_1} \right] \\ &= {\scriptsize (8.99 × 10^9 Nm^2/C^2)(5.0 × 10^{- 9}C)(3.0 × 10^{-9} C) \left[\frac{1}{0.15 m} - \frac{1}{0.10 m} \right]} \\ &= -4.5 × 10^{-7} J \end{align*}$$Explicación
El cambio en la energía potencial es negativo, como se esperaba, e igual en magnitud al cambio en la energía cinética en este sistema. Recuerda del ejemplo 7.1 que el cambio en la energía cinética fue positivo.
 Comprueba tu aprendizaje 7.2
Comprueba tu aprendizaje 7.2
Debido a la ley de Coulomb, las fuerzas debidas a cargas múltiples en una carga de prueba $Q$ se superponen; pueden calcularse individualmente y luego agregarse.
Esto implica que las integrales de trabajo y, por lo tanto, las energías potenciales resultantes muestran el mismo comportamiento. Para demostrar esto, consideramos un ejemplo de ensamblar un sistema de cuatro cargas.
Ejemplo 7.3
Ensamblando Cuatro Cargas Positivas
Encuentra la cantidad de trabajo que debe realizar un agente externo al ensamblar cuatro cargas $+ 2.0 μC$, $+ 3.0 μC$, $+ 4.0 μC$ y $+ 5.0 μC$ en los vértices de un cuadrado de $1.0 cm$ de lado, comenzando cada carga desde el infinito ().
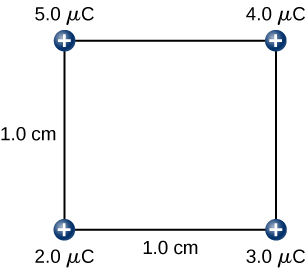
Estrategia
Traemos las cargas una a la vez, dándoles ubicaciones de inicio en el infinito y calculando el trabajo para llevarlas desde el infinito hasta su ubicación final. Hacemos esto para aumentar la carga.
Solución
Paso 1. Primero trae la carga de $+ 2.0 μC$ al origen. Como todavía no hay otras cargas a una distancia finita de esta carga, no se realiza ningún trabajo para llevarlo desde el infinito,
$$W_1 = 0.$$Paso 2. Mientras mantienes fija la carga de $+ 2.0 μC$ en el origen, lleva la carga de $+ 3.0 μC a (x, y, z) = (1.0cm, 0, 0)$ ().
Ahora, la fuerza aplicada debe funcionar contra la fuerza ejercida por la carga $+ 2.0 μC$ fijada en el origen. El trabajo realizado es igual al cambio en la energía potencial de la carga de $+ 3.0 μC$:
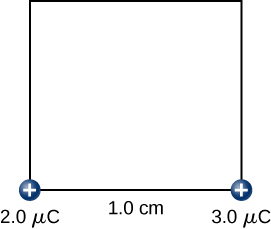
Paso 3. Mientras se mantienen fijas las cargas de $+ 2.0 μC$ y $+ 3.0 μC$ en sus lugares, lleva la carga de $+ 4.0 μC a (x, y, z) = (1.0 cm, 1.0 cm, 0)$ (). El trabajo realizado en este paso es
$$\begin{align*} W_3 &= k\frac{q_1q_3}{r_{13}} + k\frac{q_2q_3}{r_{23}} \\ &= {\scriptsize (9.0 × 10^9 \frac{N \cdot m^2}{C^2}) \left[\frac{(2.0 × 10^{−6} C)(4.0 × 10^{−6} C)}{\sqrt{2} × 10^{-2} m} + \frac{(3.0 × 10^{−6} C)(4.0 × 10^{−6} C)}{1.0 × 10^{-2} m}\right] } \\ &= 15.9J \end{align*}$$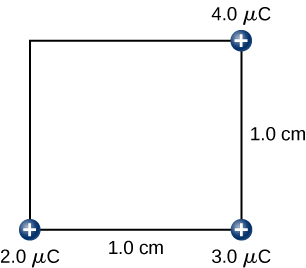
Paso 4. Finalmente, manteniendo las primeras tres cargas en su lugar, lleva la carga de $+ 5.0 μC a (x, y, z) = (0, 1.0 cm, 0)$ (). El trabajo hecho aquí es
$$\begin{align*} W_4 &= k\frac{q_1}{r_{14}} + k\frac{q_2}{r_{24}} + k\frac{q_3}{r_{34}} \\ &= {\scriptsize (9.0 × 10^9 \frac{N \cdot m^2}{C^2}) \left[\frac{(2.0 × 10^{−6} C)}{1.0 × 10^{-2} m} + \frac{(3.0 × 10^{−6} C)}{\sqrt{2} × 10^{-2} m} + \frac{(4.0 × 10^{−6} C)}{1.0 × 10^{-2} m} \right]} \\ &= 36.5J \end{align*}$$Por lo tanto, el trabajo total realizado por la fuerza aplicada al ensamblar las cuatro cargas es igual a la suma del trabajo al llevar cada carga desde el infinito hasta su posición final: $$W_T = W_1 + W_2 + W_3 + W_4 = 0 + 5.4 J + 15.9 J + 36.5 J = 57.8 J$$
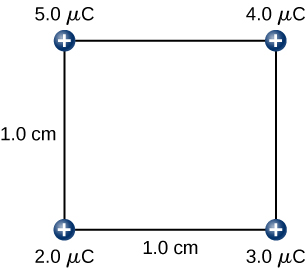
Explicación
El trabajo en cada carga depende solo de sus interacciones por pares con las otras cargas. No se deben considerar interacciones más complicadas; el trabajo en la tercera carga solo depende de su interacción con la primera y la segunda carga, la interacción entre la primera y la segunda carga no afecta a la tercera.
 Comprueba tu aprendizaje 7.3
Comprueba tu aprendizaje 7.3
Observa que la energía potencial eléctrica es positiva si las dos cargas son del mismo tipo, ya sean positivas o negativas, y negativas si las dos cargas son de tipos opuestos. Esto tiene sentido si piensas en el cambio en la energía potencial $ΔU$ a medida que acercas las dos cargas o las alejas más. Dependiendo de los tipos relativos de cargas, es posible que tengas que trabajar en el sistema o que el sistema lo hagas funcionar, es decir, que su trabajo sea positivo o negativo. Si tienes que hacer un trabajo positivo en el sistema (en realidad empujar las cargas más cerca), entonces la energía del sistema debería aumentar. Si acercas dos cargas positivas o dos cargas negativas, tienes que hacer un trabajo positivo en el sistema, lo que aumenta su energía potencial. Como la energía potencial es proporcional a $1/r$, la energía potencial aumenta cuando $r$ desciende entre dos cargas positivas o dos negativas.
Por otro lado, si acercas una carga positiva y una carga negativa, tienes que hacer un trabajo negativo en el sistema (las cargas te están jalando), lo que significa que le quitas energía al sistema. Esto reduce la energía potencial. Dado que la energía potencial es negativa en el caso de un par de cargas positivas y negativas, el aumento en $1/r$ hace que la energía potencial sea más negativa, que es lo mismo que una reducción en la energía potencial.
El resultado del Ejemplo 7.1 puede extenderse a sistemas con cualquier cantidad arbitraria de cargas. En este caso, es más conveniente escribir la fórmula como
El factor de $1/2$ explica que hay que agregar cada par de cargas dos veces.
Recordemos que antes definimos el campo eléctrico como una cantidad independiente de la carga de prueba en un sistema dado, lo que no obstante nos permitiría calcular la fuerza que resultaría en una carga de prueba arbitraria (la suposición por defecto en ausencia de otra información es que la carga de prueba es positiva). Definimos brevemente un campo para la gravedad, pero la gravedad siempre es atractiva, mientras que la fuerza eléctrica puede ser atractiva o repulsiva. Por lo tanto, aunque la energía potencial es perfectamente adecuada en un sistema gravitatorio, es conveniente definir una cantidad que nos permita calcular el trabajo con una carga independiente de la magnitud de la carga. Calcular el trabajo directamente puede ser difícil, ya que $W = \overrightarrow{\bold{F}} \cdot \overrightarrow{\bold{d}}$ y la dirección y magnitud de $\overrightarrow{\bold{F}}$ pueden ser complejas para cargas múltiples, para objetos de forma extraña y a lo largo de trayectos arbitrarios. Pero sí sabemos que debido a que $\overrightarrow{\bold{F}} = q\overrightarrow{\bold{E}}$, el trabajo, y por lo tanto $ΔU$, es proporcional a la carga de prueba $q$. Para tener una cantidad física que sea independiente de la carga de prueba, definimos el potencial eléctrico $V$ (o simplemente potencial, así se entiende en electricidad) es la energía potencial por unidad de carga:
Potencial eléctrico
La energía potencial eléctrica por carga unitaria es
$$V = \frac{U}{q} \tag{7.4}$$Como $U$ es proporcional a $q$, la dependencia de $q$ se cancela. Por lo tanto, $V$ no depende de $q$. El cambio en la energía potencial $ΔU$ es crucial, por lo que nos preocupa la diferencia en la diferencia potencial o potencial $ΔV$ entre dos puntos, donde
$$ΔV = V_B − V_A = \frac{ΔU}{q}$$Diferencia de potencial eléctrico
La diferencia de potencial eléctrico entre los puntos $A$ y $B$, $V_B − V_A$, se define como el cambio en la energía potencial de una carga $q$ movida de $A$ a $B$, dividida por la carga. Las unidades de la diferencia de potencial son joules por coulomb, dando el nombre de voltio ($V$) en honor a Alessandro Volta.
$$1V = 1J/C$$El término familiar de voltaje es el nombre común para la diferencia de potencial eléctrico. Ten en cuenta que cuando se cita una tensión, se entiende que es la diferencia de potencial entre dos puntos. Por ejemplo, cada batería tiene dos terminales, y su voltaje es la diferencia de potencial entre ellos. Más fundamentalmente, el punto que elijas como cero voltios es arbitrario. Esto es análogo al hecho de que la energía potencial gravitacional tiene un cero arbitrario, como el nivel del mar o quizás el piso de una sala de conferencias. Vale la pena enfatizar la distinción entre diferencia de potencial y energía potencial eléctrica.
Diferencia de potencial y energía eléctrica potencial
La relación entre la diferencia de potencial (o voltaje) y la energía potencial eléctrica está dada por
$$ΔV = \frac{ΔU}{q} o ΔU = qΔV \tag{7.5}$$Ejemplo 7.4
Calculando Energía
Tienes una batería de motocicleta de $12.0 V$ que puede mover $5000 C$ de carga y una batería de automóvil de $12.0 V$ que puede mover $60,000 C$ de carga. ¿Cuánta energía entrega cada uno? (Supón que el valor numérico de cada carga es exacto a tres cifras significativas).
Estrategia
Decir que tenemos una batería de $12.0 V$ significa que sus terminales tienen una diferencia de potencial de $12.0 V$. Cuando una batería de ese tipo se mueve, coloca la carga a través de una diferencia de potencial de $12.0 V$, y la carga recibe un cambio en la energía potencial igual a $ΔU = qΔV$. Para encontrar la salida de energía, multiplicamos la carga movida por la diferencia de potencial.
Solución
Para la batería de la motocicleta, $q = 5000C$ y $ΔV = 12.0V$. La energía total entregada por la batería de la motocicleta es
$$ΔU_{\textsf{moto}} = (5000 C)(12.0 V) = (5000 C)(12.0 J/C) = 6.00 × 10^4 J$$Del mismo modo, para la batería del automóvil, $q = 60,000 C$ y
$$ΔU_{\textsf{auto}} = (60,000 C)(12.0 V) = 7.20 × 10^5 J$$Explicación
El voltaje y la energía están relacionados, pero no son lo mismo. Los voltajes de las baterías son idénticos, pero la energía suministrada por cada uno es bastante diferente. Una batería de automóvil tiene un motor mucho más grande para arrancar que una motocicleta. Ten en cuenta también que cuando una batería se descarga, parte de su energía se utiliza internamente y su voltaje de la terminal cae, como cuando los faros se atenúan debido a una batería de automóvil agotada. La energía suministrada por la batería todavía se calcula como en este ejemplo, pero no toda la energía está disponible para uso externo.
 Comprueba tu aprendizaje 7.4
Comprueba tu aprendizaje 7.4
Observa que las energías calculadas en el ejemplo anterior son valores absolutos. El cambio en la energía potencial de la batería es negativo, ya que pierde energía. Estas baterías, como muchos sistemas eléctricos, en realidad mueven electrones de carga negativos en particular. Las baterías repelen los electrones de sus terminales negativos ($A$) a través de cualquier circuito involucrado y los atraen a sus terminales positivos ($B$), como se muestra en la . El cambio en el potencial es $ΔV = V_B − V_A = + 12 V$ y la carga $q$ es negativa, por lo que $ΔU = qΔV$ es negativo, lo que significa que la energía potencial de la batería ha disminuido cuando $q$ se ha movido de $A$ a $B$.
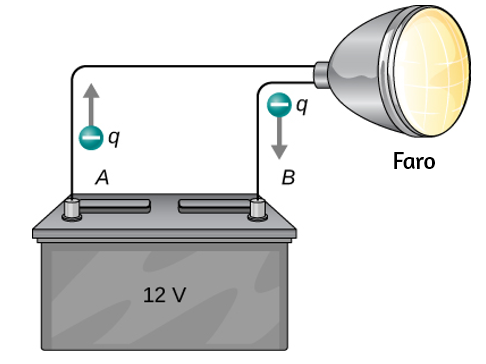
Ejemplo 7.5
¿Cuántos electrones se mueven a través de un faro cada segundo?
Cuando una batería de automóvil de $12.0 V$ enciende un solo faro de $30.0 W$, ¿cuántos electrones pasan a través de él cada segundo?
Estrategia
Para encontrar el número de electrones, primero debemos encontrar la carga que se mueve en $1.00 s$. La carga movida está relacionada con el voltaje y la energía a través de las ecuaciones $ΔU = qΔV$. Una lámpara de $30.0 W$ usa $30.0$ julios por segundo. Como la batería pierde energía, tenemos que $ΔU = -30 J$ y, como los electrones van del terminal negativo al positivo, vemos que $ΔV = + 12.0 V$.
Solución
Para encontrar la carga q movida, resolvemos la ecuación $ΔU = qΔV$:
$$q = \frac{ΔU}{ΔV}$$Ingresando los valores para $ΔU$ y $ΔV$, obtenemos
$$q = \frac{−30.0 J}{+12.0 V} = \frac{−30.0 J}{+12.0 J/C} = −2.50 C$$La cantidad de electrones n_e es la carga total dividida por la carga por electrón. Es decir,
$$n_e = \frac{-2.50 C}{−1.60 × 10^{−19}C/e^−}$$Explicación
Este es un número muy grande. No es de extrañar que normalmente no observemos electrones individuales con tantos presentes en sistemas ordinarios. De hecho, la electricidad había estado en uso durante muchas décadas antes de que se determinara que las cargas móviles en muchas circunstancias eran negativas. La carga positiva que se mueve en la dirección opuesta a la carga negativa a menudo produce efectos idénticos; esto hace que sea difícil determinar qué se está moviendo o si ambos se están moviendo.
 Comprueba tu aprendizaje 7.5
Comprueba tu aprendizaje 7.5
La energía por electrón es muy pequeña en situaciones macroscópicas como la del ejemplo anterior, una pequeña fracción de un joule. Pero en una escala submicroscópica, dicha energía por partícula (electrón, protón o ion) puede ser de gran importancia.
Por ejemplo, incluso una pequeña fracción de un joule puede ser lo suficientemente grande como para que estas partículas destruyan las moléculas orgánicas y dañen el tejido vivo. La partícula puede hacer daño por colisión directa, o puede crear rayos X dañinos, que también pueden infligir daño. Es útil tener una unidad de energía relacionada con los efectos submicroscópicos.
La muestra una situación relacionada con la definición de dicha unidad de energía. Un electrón se acelera entre dos placas de metal cargadas, como podría ser en un tubo de televisión o un osciloscopio de modelo antiguo. El electrón gana energía cinética que luego se convierte en otra forma-luz en el tubo de televisión, por ejemplo (ten en cuenta que en términos de energía, "cuesta abajo" para el electrón es "cuesta arriba" para una carga positiva). Dado que la energía está relacionada con el voltaje por $ΔU = qΔV$, podemos pensar en el joule como un coulomb-voltio.
Electrón-Voltio
En la escala submicroscópica, es más conveniente definir una unidad de energía llamada electrón-voltio ($eV$), que es la energía que se le da a una carga fundamental acelerada a través de una diferencia de potencial de $1 V$. En forma de ecuación,
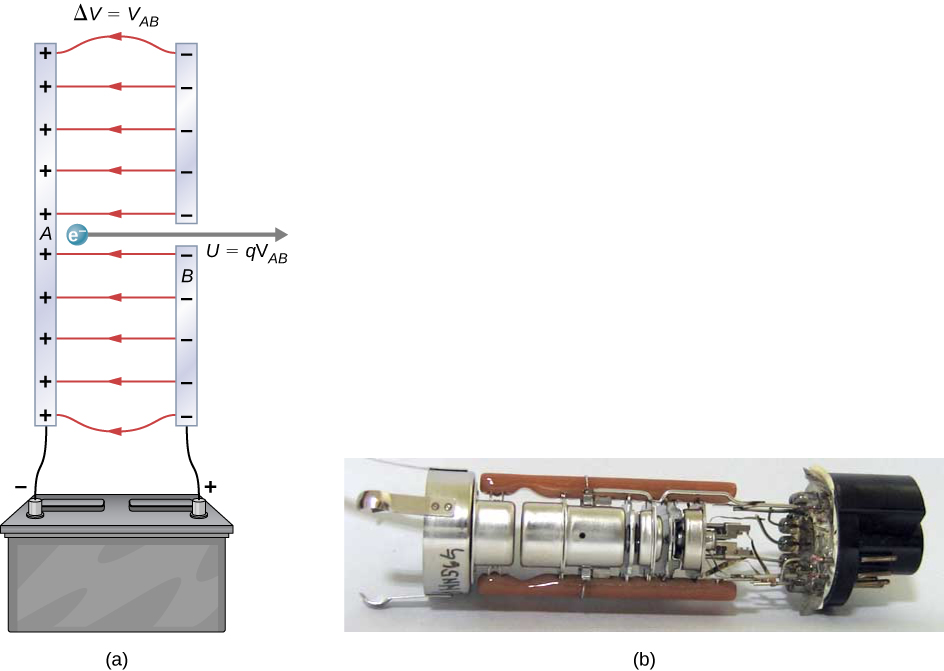
Un electrón acelerado a través de una diferencia de potencial de $1 V$ recibe una energía de $1 eV$. Se deduce que un electrón acelerado a través de $50 V$ gana $50 eV$. Una diferencia de potencial de $100.000 V$ $(100 kV)$ proporciona a un electrón una energía de $100.000 eV$ $(100 keV)$, y así sucesivamente. De manera similar, un ion con una doble carga positiva acelerada a través de $100 V$ gana $200 eV$ de energía. Estas relaciones simples entre el voltaje de aceleración y las cargas de partículas hacen que el electrón-voltio sea una unidad de energía simple y conveniente en tales circunstancias.
El electrón-voltio se emplea comúnmente en procesos submicroscópicos: las energías de valencia química y las energías de enlace molecular y nuclear se encuentran entre las cantidades expresadas a menudo en electrón-voltios. Por ejemplo, se requieren aproximadamente $5 eV $de energía para romper ciertas moléculas orgánicas. Si un protón se acelera desde el reposo a través de una diferencia de potencial de $30 kV$, adquiere una energía de $30 keV$ $(30,000 eV)$ y puede romper hasta $6000$ de estas moléculas $(30,000eV ÷ 5eV$ por molécula $= 6000$ moléculas). Las energías de descomposición nuclear son del orden de $1 MeV$ $(1,000,000 eV)$ por evento y pueden producir un daño biológico significativo.
La energía total de un sistema se conserva si no hay una adición neta (o resta) debido al trabajo o la transferencia de calor. Para las fuerzas conservadoras, como la fuerza electrostática, la conservación de la energía indica que la energía mecánica es una constante.
La energía mecánica es la suma de la energía cinética y la energía potencial de un sistema; es decir, $K + U = constante$. Una pérdida de $U$ para una partícula cargada se convierte en un aumento en su $K$.
La conservación de energía se expresa en forma de ecuación como
$$K + U = constante$$o $$K_i + U_i = K_f + U_f$$
donde $i$ y $f$ representan las condiciones iniciales y finales. Como lo hemos encontrado muchas veces antes, considerar la energía nos puede dar ideas y facilitar la resolución de problemas.
Ejemplo 7.6
Energía potencial eléctrica convertida en energía cinética
Calcula la velocidad final de un electrón libre acelerado desde el reposo a través de una diferencia de potencial de $100 V$ (supón que este valor numérico es exacto a tres cifras significativas).
Estrategia
Tenemos un sistema con solo fuerzas conservadoras. Suponiendo que el electrón se acelera en el vacío y despreciando la fuerza de la gravedad (comprobaremos esta suposición más adelante), toda la energía potencial eléctrica se convierte en energía cinética. Podemos identificar las formas de energía inicial y final que serán $K_i = 0$, $K_f = \frac{1}{2}mv^2$, $U_i = qV$, $U_f = 0$.
Solución
La conservación de energía establece que
$$K_i + U_i = K_f + U_f$$Ingresando las fórmulas identificadas anteriormente, obtenemos
$$qV = \frac{mv^2}{2}$$Solucionamos esto para $v$:
$$v = \sqrt{2qV/m}$$Al ingresar valores para $q$, $V$ y $m$ obtenemos:
Explicación
Observa que tanto la carga como la tensión inicial son negativas, como en la . A partir de la discusión de la carga eléctrica y el campo eléctrico, sabemos que las fuerzas electrostáticas en partículas pequeñas son generalmente muy grandes en comparación con la fuerza gravitacional. La gran velocidad final confirma que la fuerza gravitacional es de hecho insignificante aquí.
La gran velocidad también indica cuán fácil es acelerar electrones con pequeños voltajes debido a su muy pequeña masa. Los voltajes mucho más altos que los $100 V$ en este problema se usan típicamente en cañones de electrones. Estos voltajes más altos producen velocidades de electrones tan grandes que los efectos de la relatividad especial deben tenerse en cuenta y, por lo tanto, están reservados para un capítulo posterior (Relatividad). Es por eso que consideramos un bajo voltaje (precisión) en este ejemplo.
 Comprueba tu aprendizaje 7.6
Comprueba tu aprendizaje 7.6
Hasta ahora, hemos explorado la relación entre el voltaje y la energía. Ahora queremos explorar la relación entre el voltaje y el campo eléctrico. Comenzaremos con el caso general para un campo $\overrightarrow{\bold{E}}$ no uniforme. Recuerda que nuestra fórmula general para la energía potencial de una carga de prueba $q$ en el punto $P$ con respecto al punto de referencia $R$ es
Cuando lo sustituimos en la definición de campo eléctrico ($\overrightarrow{\bold{E}} = \overrightarrow{\bold{F}}/q$), esto se convierte en
$$U_P = -q\int_R^{P} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$$Aplicando nuestra definición de potencial ($V = U/q$) a esta energía potencial, encontramos que, en general,
De nuestra discusión anterior de la energía potencial de una carga en un campo eléctrico, el resultado es independiente del camino elegido, y por lo tanto podemos elegir el camino integral que sea más conveniente.
Considera el caso especial de una carga puntual positiva q en el origen. Para calcular el potencial causado por q a una distancia r del origen relativa a una referencia de $0$ en el infinito (recuerda que hicimos lo mismo para la energía potencial), sea $P = r$ y $R = ∞$, con $d\overrightarrow{\bold{l}} = d\overrightarrow{\bold{r}} = \^{r}dr$ y usa $\overrightarrow{\bold{E}} = \frac{kq}{r^2}\^{r}$. Cuando evaluamos la integral
$$V_P = -\int_R^{P} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$$para este sistema, tenemos
$$V_r = - \int_{∞}^{r} \frac{kq}{r^2}\^{r} \cdot \^{r}dr$$que simplificado es
$$V_r = - \int_{∞}^{r} \frac{kq}{r^2}dr = \frac{kq}{r} - \frac{kq}{∞} = \frac{kq}{r}$$El resultado
$$V_r = \frac{kq}{r}$$es la forma estándar del potencial de una carga puntual. Esto se explorará más a fondo en la siguiente sección.
Para examinar otro caso especial interesante, supongamos que se produce un campo eléctrico uniforme $\overrightarrow{\bold{E}}$ colocando una diferencia de potencial (o voltaje) $ΔV$ en dos placas de metal paralelas, etiquetadas $A$ y $B$ (). El examen de esta situación nos dirá qué voltaje se necesita para producir una cierta intensidad de campo eléctrico. También revelará una relación más fundamental entre el potencial eléctrico y el campo eléctrico.
Desde el punto de vista de un físico, ya sea $ΔV$ o $\overrightarrow{\bold{E}}$ pueden usarse para describir cualquier interacción entre cargas. Sin embargo, $ΔV$ es una cantidad escalar y no tiene dirección, mientras que $\overrightarrow{\bold{E}}$ es una cantidad vectorial, que tiene tanto magnitud como dirección (ten en cuenta que la magnitud del campo eléctrico, una cantidad escalar, se representa por $E$). La relación entre $ΔV$ y $\overrightarrow{\bold{E}}$ se revela al calcular el trabajo realizado por la fuerza eléctrica al mover una carga del punto $A$ al punto $B$.
Pero como se señaló anteriormente, las distribuciones de cargas arbitrarias requieren cálculo. Por lo tanto, consideramos un campo eléctrico uniforme como un caso especial interesante.
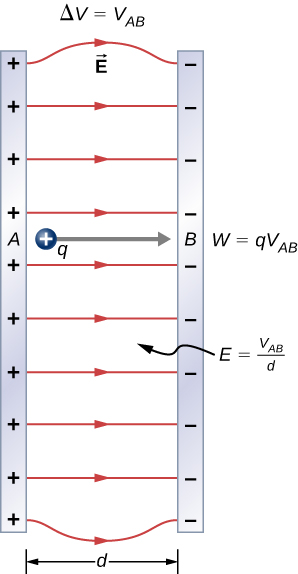
El trabajo realizado por el campo eléctrico en la para mover una carga positiva $q$ de $A$, la placa positiva de mayor potencial, a $B$, la placa negativa de menor potencial, es
$$W = -ΔU = -qΔV$$La diferencia de potencial entre los puntos $A$ y $B$ es
$$-ΔV = - (V_B - V_A) = V_A - V_B = v$$Ingresando esto en la expresión para trabajo
$$W = qV_{AB}$$El trabajo es $W = \overrightarrow{\bold{F}} \cdot \overrightarrow{\bold{d}} = Fdcosθ$; aquí $cosθ = 1$, ya que el camino es paralelo al campo. Por lo tanto, $W = Fd$. Como $F = qE$, vemos que $W = qEd$.
Sustituyendo esta expresión por el trabajo en la ecuación anterior da
$$qEd = qV_{AB}$$La carga se cancela, entonces obtenemos el voltaje entre los puntos $A$ y $B$
$$\begin{rcases} V_{AB} = Ed \\ E = \frac{V_{AB}}{d} \end{rcases} \textsf{únicamente campo uniforme}$$donde $d$ es la distancia de $A$ a $B$, o la distancia entre las placas en la . Ten en cuenta que esta ecuación implica que las unidades para el campo eléctrico son voltios por metro. Ya sabemos que las unidades para el campo eléctrico son newtons por culombio; por lo tanto, la siguiente relación entre unidades es válida:
Además, podemos extender esto a la forma integral. Sustituyendo la Ecuación 7.5 en nuestra definición por la diferencia de potencial entre los puntos $A$ y $B$, obtenemos
$$V_{BA} = V_B - V_A = −\int_R^{B} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}} + \int_R^{A} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$$que se simplifica a
$$V_B - V_A = −\int_A^{B} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$$Como demostración, a partir de esto podemos calcular la diferencia de potencial entre dos puntos ($A$ y $B$) equidistantes de una carga puntual $q$ en el origen, como se muestra en la .
Para hacer esto, integramos alrededor de un arco del círculo de radio constante $r$ entre $A$ y $B$, lo que significa que dejamos $d\overrightarrow{\bold{l}} = r\^{φ}dφ$, mientras usamos $\overrightarrow{\bold{E}} = \dfrac{kq}{r^2}\^{r}$. Así,
para este sistema se convierte
$$V_B - V_A = −\int_A^{B} \frac{kq}{r^2 }\^{r} \cdot r\^{φdφ}$$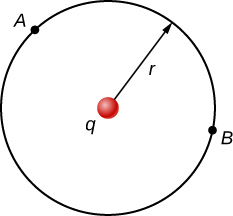
Sin embargo, $\^{r} \cdot \^{φ} = 0$ y por lo tanto
$$V_B - V_A = 0.$$Este resultado, donde no hay diferencia en el potencial a lo largo de un radio constante desde una carga puntual, será útil cuando mapeamos potenciales.
Ejemplo 7.7
¿Cuál es el voltaje más alto posible entre dos placas?
El aire seco puede soportar una fuerza de campo eléctrico máxima de aproximadamente $3,0 × 10^6 V/m$. Por encima de ese valor, el campo crea suficiente ionización en el aire para hacer que el aire sea un conductor. Esto permite una descarga o chispa que reduce el campo. ¿Cuál es, entonces, la tensión máxima entre dos placas conductoras paralelas separadas por $2,5 cm$ de aire seco?
Estrategia
Se nos da el campo eléctrico máximo $E$ entre las placas y la distancia $d$ entre ellas. Podemos usar la ecuación $V_{AB} = Ed$ para calcular la tensión máxima.
Solución
La diferencia de potencial o voltaje entre las placas es
$$V_{AB} = Ed.$$Al ingresar los valores dados para $E$ y $d$ da
$$V_{AB} = (3.0 × 10^6 V/m)(0.025 m) = 7.5 × 10^4 V$$o $$V_{AB} = 75 kV.$$
La respuesta se cita con solo dos dígitos, ya que la intensidad de campo máxima es aproximada.
Explicación
Una de las implicaciones de este resultado es que se requieren aproximadamente $75 kV$ para hacer que una chispa salte a través de un espacio de $2,5 cm$ ($1 in$), o $150 kV$ para una chispa de $5 cm$. Esto limita los voltajes que pueden existir entre los conductores, tal vez en una línea de transmisión de energía. Un voltaje más pequeño puede causar una chispa si hay aristas en la superficie, ya que los puntos filosos tienen mayores intensidades de campo que las superficies lisas. El aire húmedo se descompone a una intensidad de campo más baja, lo que significa que un voltaje más pequeño hará que una chispa salte a través del aire húmedo. Los voltajes más grandes pueden acumularse con electricidad estática en días secos ().

Ejemplo 7.8
Campo y fuerza dentro de una pistola de electrones
Un cañón de electrones () tiene placas paralelas separadas por $4.00 cm$ y les da a los electrones $25.0 keV$ de energía. (a) ¿Cuál es la intensidad del campo eléctrico entre las placas? (b) ¿Qué fuerza ejercería este campo sobre un trozo de plástico con una carga de $0.500 μC$ que se interpone entre las placas?
Estrategia
Dado que se proporcionan la separación de voltaje y placa, la intensidad del campo eléctrico se puede calcular directamente a partir de la expresión $E = V_{AB}d$. Una vez que conocemos la intensidad del campo eléctrico, podemos encontrar la fuerza en una carga usando $\overrightarrow{\bold{F}} = q\overrightarrow{\bold{E}}$.
Dado que el campo eléctrico está en una sola dirección, podemos escribir esta ecuación en términos de las magnitudes, $F = qE$.
Solución
a. La expresión de la magnitud del campo eléctrico entre dos placas de metal uniformes es
$$E = \frac{V_{AB}}{d}$$Como el electrón es una sola carga y recibe $25.0 keV$ de energía, la diferencia de potencial debe ser de $25.0 kV$.
Introduciendo este valor para $V_{AB}$ y la separación de la placa de $0.0400 m$, obtenemos
$$E = \frac{25.0 kV}{0.0400 m} = 6.25 × 10^5 V/m$$b. La magnitud de la fuerza sobre una carga en un campo eléctrico se obtiene de la ecuación
$$F = qE$$Sustituyendo los valores conocidos, obtenemos:
$$F = (0.500 × 10^{-6} C)(6.25 × 10^5 V/m) = 0.313 N$$Explicación
Ten en cuenta que las unidades son newtons, ya que $1 V/m = 1 N/C.$ Debido a que el campo eléctrico es uniforme entre las placas, la fuerza sobre la carga es la misma sin importar dónde esté ubicada la carga entre las placas.
Ejemplo 7.9
Cálculo del potencial de un punto de carga
Dada una carga puntual $q = + 2.0 nC$ en el origen, calcula la diferencia de potencial entre el punto $P_1$ una distancia $a = 4.0 cm$ desde $q$, y $P_2$ una distancia $b = 12.0 cm$ desde $q$, donde los dos puntos tienen un ángulo de $φ = 24°$ entre ellos ().
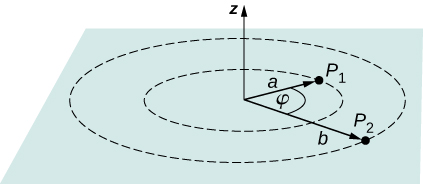
Estrategia
Haz esto en dos pasos. El primer paso es usar $V_B - V_A = -\int_A^{B} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$, con $A = a = 4.0 cm$ y $B = b = 12.0 cm$, con $d\overrightarrow{\bold{l}} = d\overrightarrow{\bold{r}} = \^{r}dr y \overrightarrow{\bold{E}} = \frac{kq}{r^2}\^{r}$. Luego realiza la integral. El segundo paso es integrar $V_B - V_A = -\int_A^{B} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$ alrededor de un arco de radio constante $r$, lo que significa que dejamos $d\overrightarrow{\bold{l}} = r\overrightarrow{φ}dφ$ con límites $0 ≤ φ ≤ 24°$, aún usando $\overrightarrow{\bold{E}} = \frac{kq}{r^2}\^{r}$. Luego agrega los dos resultados juntos.
Solución
Para la primera parte, $V_B - V_A = -\int_A^{B} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$, para este sistema se convierte en $V_b - V_a = -\int_a^{b} \frac{kq}{r^2}\^{r} \cdot \^{r}dr$, que se computa para:
$$\begin{split} ΔV &= -\int_a^{b} \frac{kq}{r^2}dr = kq \left[\frac{1}{a} - \frac{1}{b} \right] \\ &= {\footnotesize (8.99 × 10^9 Nm^2/C^2)(2.0 × 10^{-9} C) \left[\frac{1}{0.040 m} − \frac{1}{0.12 m} \right] = 300V } \end{split}$$Para el segundo paso, $V_B - V_A = -\int_A^{B} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$, se convierte en $ΔV = -\int_0^{{24°}} \frac{kq}{r^2}\^{r} \cdot r \^{φ}dφ$, pero $\^{r} \cdot \^{φ} = 0$, y por lo tanto $ΔV = 0$. Sumando las dos partes, obtenemos $300 V$.
Explicación
Hemos demostrado el uso de la forma integral de la diferencia de potencial para obtener un resultado numérico. Observa que, en este sistema en particular, también podríamos haber usado la fórmula para el potencial debido a una carga puntual en los dos puntos y simplemente tomar la diferencia.
 Comprueba tu aprendizaje 7.7
Comprueba tu aprendizaje 7.7
Antes de presentar problemas relacionados con la electrostática, sugerimos una estrategia de resolución de problemas a seguir para este tema.
Estrategia de resolución de problemas: Electrostática
Las cargas puntuales, como los electrones, se encuentran entre los elementos fundamentales de la materia. Además, las distribuciones de carga esférica (como la carga en una esfera de metal) crean campos eléctricos externos exactamente como una carga puntual.
El potencial eléctrico debido a una carga puntual es, por lo tanto, un caso que debemos tener en cuenta.
Podemos usar el cálculo para encontrar el trabajo necesario para mover una carga de prueba $q$ desde una gran distancia a una distancia $r$ de una carga puntual $q$. Al observar la conexión entre el trabajo y el potencial $W = -qΔV$, como en la última sección, podemos obtener el siguiente resultado.
Potencial eléctrico v de una carga puntual
El potencial eléctrico V de una carga puntual viene dado por
$$V = \frac{kq}{r} (\textsf{carga puntual}) \tag{7.8}$$donde $k$ es una constante igual a $8.99 × 10^9 N \cdot m^2/C^2$
El potencial en el infinito se elige para ser cero. Por lo tanto, $V$ para una carga puntual disminuye con la distancia, mientras que $\overrightarrow{\bold{E}}$ para una carga puntual disminuye con la distancia al cuadrado:
$$E = \frac{F}{q_t} = \frac{kq}{r^2}$$Recuerda que el potencial eléctrico $V$ es escalar y no tiene dirección, mientras que el campo eléctrico $\overrightarrow{\bold{E}}$ es un vector. Para encontrar el voltaje debido a una combinación de cargas puntuales, agrega los voltajes individuales como números. Para encontrar el campo eléctrico total, debes agregar los campos individuales como vectores, teniendo en cuenta la magnitud y la dirección. Esto es consistente con el hecho de que $V$ está estrechamente asociado con la energía, un escalar, mientras que $\overrightarrow{\bold{E}}$ está estrechamente asociado con la fuerza, un vector.
Ejemplo 7.10
¿Qué voltaje es producido por una pequeña carga en una esfera de metal?
Las cargas en electricidad estática están típicamente en el rango de nanocoulomb ($nC$) a microcoulomb ($μC$). ¿Cuál es el voltaje a $5.00 cm$ de distancia del centro de una esfera metálica sólida de $1 cm$ de diámetro que tiene una carga estática de $-3.00 nC$?
Estrategia
La carga sobre una esfera de metal se extiende uniformemente y produce un campo como el de una carga puntual ubicada en su centro. Por lo tanto, podemos encontrar el voltaje usando la ecuación $V = \dfrac{kq}{r}$.
Solución
Ingresando valores conocidos en la expresión para el potencial de una carga puntual, obtenemos
$$V = k\frac{q}{r} = (8.99 × 10^9 N \cdot m^2/C^2) \left(\frac{−3.00 × 10^{-9} C}{5.00 × 10^{-2} m} \right) = −539 V$$Explicación
El valor negativo para el voltaje significa que se atraería una carga positiva desde una distancia mayor, ya que el potencial es más bajo (más negativo) que a distancias más grandes. Por el contrario, una carga negativa sería repelida, como se esperaba.
Ejemplo 7.11
¿Cuál es el exceso de carga en un generador Van de Graaff?
Un generador Van de Graaff de demostración tiene una esfera metálica de $25.0 cm$ de diámetro que produce un voltaje de $100 kV$ cerca de su superficie (). ¿Qué exceso de carga reside en la esfera? (Supón que cada valor numérico aquí se muestra con tres cifras significativas).
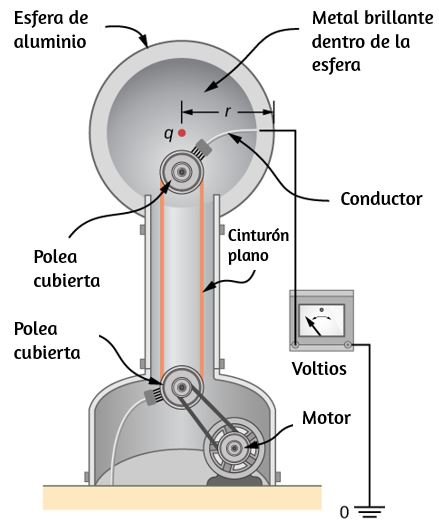
Estrategia
El potencial en la superficie es el mismo que el de una carga puntual en el centro de la esfera, a $12.5$ cm de distancia (El radio de la esfera es $12.5 cm$). Podemos determinar el exceso de carga usando la ecuación
$$V = k\frac{q}{r}$$Solución
Al resolver para q e ingresar valores conocidos, obtenemos
$$q = \frac{rV}{k} = \frac{(0.125 m)(100 × 10^3 V)}{8.99 × 10^9 N \cdot m^2/C^2} = 1.39 × 10^{-6} C = 1.39 μC$$Explicación
Esta es una carga relativamente pequeña, pero produce un voltaje bastante grande. Aquí tenemos otra indicación de que es difícil almacenar cargas aisladas.
 Comprueba tu aprendizaje 7.8
Comprueba tu aprendizaje 7.8
Los voltajes en ambos ejemplos podrían medirse con un medidor que compare el potencial medido con el potencial de tierra. El potencial de tierra a menudo se toma como cero (en lugar de tomar el potencial en el infinito para que sea cero).
Es la diferencia de potencial entre dos puntos lo que es importante, y muy a menudo hay una suposición tácita de que algún punto de referencia, como la Tierra o un punto muy distante, tiene un potencial cero. Como se señaló anteriormente, esto es análogo a tomar el nivel del mar como $h = 0$ cuando se considera la energía potencial gravitacional $U_g = mgh$.
Así como el campo eléctrico obedece a un principio de superposición, también lo hace el potencial eléctrico. Considera un sistema que consiste en $N$ cargas $q_1, q_2, ..., q_N$.
¿Cuál es el potencial eléctrico neto $V$ en un punto espacial $P$ de estas cargas? Cada una de estas cargas es una carga fuente que produce su propio potencial eléctrico en el punto $P$, independientemente de cualquier otro cambio que pueda estar haciendo. Sean $V_1, V_2, ..., V_N$ los potenciales eléctricos en $P$ producidos por las cargas $q_1, q_2, ..., q_N$, respectivamente. Entonces, el $V_P$ de potencial eléctrico neto en ese punto es igual a la suma de estos potenciales eléctricos individuales. Puedes mostrar esto fácilmente calculando la energía potencial de una carga de prueba cuando lleva la carga de prueba desde el punto de referencia en el infinito hasta el punto $P$: $$V_P = V_1 + V_2 + ..., V_N = \sum_1^{N} V_i$$
Observa que el potencial eléctrico sigue el mismo principio de superposición que el campo eléctrico y la energía potencial eléctrica. Para mostrar esto más explícitamente, ten en cuenta que una carga de prueba $q_i$ en el punto $P$ en el espacio tiene distancias de $r_1, r_2, ..., r_N$ de las cargas $N$ fijadas en el espacio superior, como se muestra en la .
Usando nuestra fórmula para el potencial de una carga puntual por cada una de estas cargas (suponiendo que son puntuales), encontramos que
Por lo tanto, la energía potencial eléctrica de la carga de prueba es
$$U_P = q_tV_P = q_tk\sum_1^{N} \frac{q_i}{r_i}$$que es lo mismo que el trabajo para llevar la carga de prueba al sistema, como se encuentra en la primera sección del capítulo.
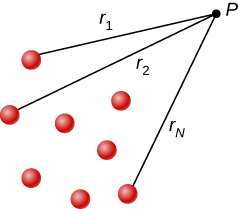
Un dipolo eléctrico es un sistema de dos cargas iguales pero opuestas a una distancia fija. Este sistema se usa para modelar muchos sistemas del mundo real, incluidas las interacciones atómicas y moleculares. Uno de estos sistemas es la molécula de agua, bajo ciertas circunstancias. Estas circunstancias se cumplen dentro de un horno de microondas, donde los campos eléctricos con direcciones alternas hacen que las moléculas de agua cambien de orientación. Esta vibración es la misma que el calor a nivel molecular.
Ejemplo 7.12
Potencial eléctrico de un dipolo
Considera el dipolo de la con la magnitud de carga de $q = 3.0 nC$ y la distancia de separación $d = 4.0 cm$. ¿Cuál es el potencial en los siguientes lugares en el espacio? (a) $(0, 0, 1,0 cm)$; (b) $(0, 0, -5,0 cm)$; (c) $(3.0 cm, 0, 2.0 cm)$.
Estrategia
Aplica $\displaystyle V_P = k\sum_1^{N} \frac{q_i}{r_i}$ a cada uno de estos tres puntos.
Solución
a. $\displaystyle V_P = k\sum_1^{N} \frac{q_i}{r_i} = (9.0 × 10^9 N \cdot m^2/C^2) \left(\frac{3.0 nC}{0.010 m} − \frac{3.0 nC}{0.030 m} \right) = 1.8 × 10^2 V$
b. $\displaystyle V_P = k\sum_1^{N} \frac{q_i}{r_i} = (9.0 × 10^9 N \cdot m^2/C^2) \left(\frac{3.0 nC}{0.070 m} − \frac{3.0 nC}{0.030 m} \right) = -5.1 × 10^2 V$
c. $\displaystyle V_P = k\sum_1^{N} \frac{q_i}{r_i} = (9.0 × 10^9 N \cdot m^2/C^2) \left(\frac{3.0 nC}{0.030 m} − \frac{3.0 nC}{0.050 m} \right) = 3.6 × 10^2 V$
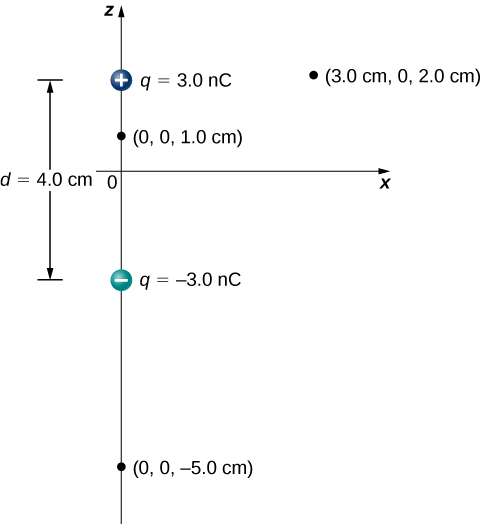
Explicación
Observa que el potencial calculado es significativamente más simple que el campo eléctrico, debido a que el potencial es un escalar en lugar de un vector.
 Comprueba tu aprendizaje 7.9
Comprueba tu aprendizaje 7.9
La siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, permite hallar el potencial eléctrico para las posiciones del $P$ del ejemplo anterior y, además, para otras posiciones, separaciones y valores de las cargas. Practica con la escena desplazando el punto $P$ y cambiando los valores de $d$ y $q$
Ahora consideremos el caso especial cuando la distancia del punto $P$ desde el dipolo es mucho mayor que la distancia entre las cargas en el dipolo, $r >> d$; por ejemplo, cuando estamos interesados en el potencial eléctrico debido a una molécula polarizada, como una molécula de agua. Esto no es tan lejos (infinito) que simplemente podemos tratar el potencial como cero, pero la distancia es lo suficientemente grande como para que podamos simplificar nuestros cálculos en relación con el ejemplo anterior.
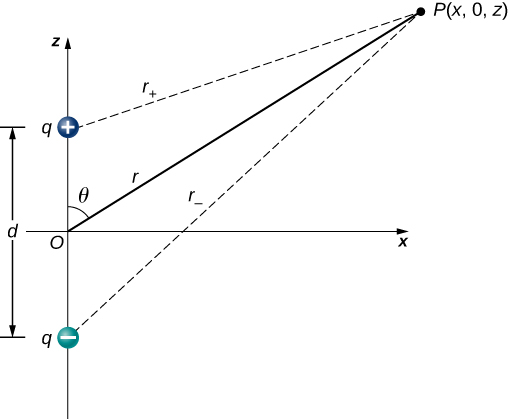
donde
$$r ± = \sqrt{x^2 + \left(z ± \frac{d}{2} \right)^2}$$Esta sigue siendo la fórmula exacta. Para aprovechar el hecho de que $r >> d$, reescribimos los radios en términos de coordenadas polares, con $x = rsenθ$ y $z = rcosθ$. Esto nos da
$$r ± = \sqrt{r^2 sen^2θ + \left(rcosθ ± \frac{d}{2} \right)^2}$$Podemos simplificar esta expresión sacando r de la raíz,
$$r ± = r \sqrt{sen^2θ + \left(cosθ ± \frac{d}{2} \right)^2}$$y luego multiplicando los paréntesis
$$r ± = r \sqrt{sen^2θ + cos^2θ ± cosθ \frac{d}{r} \left(\frac{d}{2r} \right)^2} = r \sqrt{1 ± cosθ \frac{d}{r} \left(\frac{d}{2r} \right)^2}$$El último término en la raíz es lo suficientemente pequeño como para ser insignificante (recuerda que $r >> d$, y por lo tanto $(d/r)^2$ es extremadamente pequeño, cero al nivel que estaremos midiendo), dejándonos con
$$r ± = r \sqrt{1 ± cosθ \frac{d}{r}}$$Usando la aproximación binomial (un resultado estándar de las matemáticas de series, cuando $α$ es pequeño)
y sustituyendo esto en nuestra fórmula para $V_P$, obtenemos
$$V_P = k \left[\frac{q}{r}(1 + \frac{dcosθ}{2r}) − \frac{q}{r}(1 − \frac{dcosθ}{2r}) \right] = k\frac{qdcosθ}{r^2}$$Hemos modificado la escena interactiva, diseñada por Juan Guillermo Rivera Berrío, para hallar el potencial eléctrico utilizando la fórmula exacta y la aproximación para $r >> d$. Desplaza el punto $P$ y observa que a medida que te alejas del dipolo eléctrico, los valores calculados tienden a ser el mismo
Lo anterior se puede escribir de manera más conveniente si definimos una nueva cantidad, el momento dipolar eléctrico,
donde estos vectores apuntan desde la carga negativa a la positiva. Ten en cuenta que esto tiene una magnitud $qd$. Esta cantidad nos permite escribir el potencial en el punto $P$ debido a un dipolo en el origen como
Un diagrama de la aplicación de esta fórmula se muestra en la .
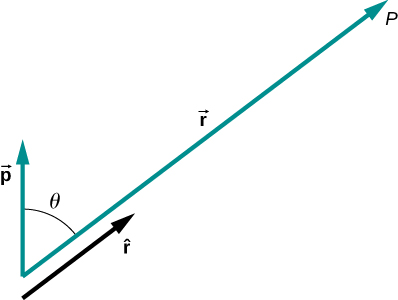
También hay momentos de orden superior, para cuadripolos, octupoles, y así sucesivamente. Verás estos en clases futuras.
Hemos estado trabajando con cargas puntuales en gran medida, pero ¿qué pasa con las distribuciones de carga continua? Recuerda de la Ecuación 7.9 que
$$V_P = k\sum_1^{N} \frac{q_i}{r_i}$$Podemos tratar una distribución de carga continua como una colección de puntos individuales infinitesimalmente separados. Esto produce la integral
para el potencial en un punto $P$. Ten en cuenta que $r$ es la distancia desde cada punto individual en la distribución de carga al punto $P$. Las cargas infinitesimales están dadas por
$$dq \begin{cases} λ dl \textsf{ (una dimensión )} \\ σ dA \textsf{ (dos dimensiones )} \\ ρ dV \textsf{ (tres dimensiones )} \end{cases}$$donde $λ$ es la densidad de carga lineal, $σ$ es la carga por unidad de área, y $ρ$ es la carga por unidad de volumen.
Ejemplo 7.13
Potencial de una carga lineal
Encuentra el potencial eléctrico de un cable no conductor con carga uniforme con densidad lineal $λ$ ($culombio/metro$) y longitud $L$ en un punto que se encuentra en una línea que divide el cable en dos partes iguales.
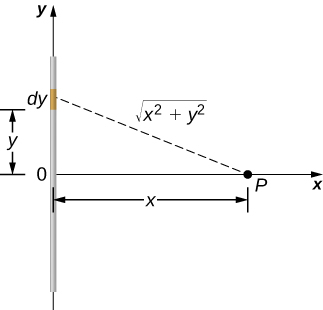
Estrategia
Para configurar el problema, elegimos coordenadas cartesianas de tal manera que explotamos la simetría del problema tanto como sea posible.
Colocamos el origen en el centro del cable y orientamos el eje $y$ a lo largo del cable de modo que los extremos del cable estén en $y = ± L/2$. El punto de campo $P$ está en el plano $xy$ y como la elección de los ejes depende de nosotros, elegimos el eje $x$ para pasar por el punto de campo $P$, como se muestra en la .
Solución
Considera un pequeño elemento de la distribución de carga entre $y$ y $y + dy$. La carga en esta celda es $dq = λdy$ y la distancia desde la celda al punto de campo $P$ es $\sqrt{x^2 + y^2}$. Por lo tanto, el potencial se convierte en
Explicación
Observa que esto era más simple que el problema equivalente para el campo eléctrico, debido al uso de cantidades escalares. Recuerda que esperamos que el nivel cero del potencial esté en el infinito, cuando tenemos una carga finita. Para examinar esto, tomamos el límite del potencial anterior cuando $x$ se aproxima al infinito; en este caso, los términos dentro del logaritmo natural se aproximan a uno, y por lo tanto el potencial se aproxima a cero en este límite. Ten en cuenta que podríamos haber hecho este problema de manera equivalente en coordenadas cilíndricas; el único efecto sería sustituir $r$ por $x$ y $z$ por $y$.
Ejemplo 7.14
Potencial debido a un anillo de carga
Un anillo tiene una densidad de carga uniforme $λ$, con unidades de culombio por unidad de metro de arco. Encuentra el potencial eléctrico en un punto en el eje que pasa por el centro del anillo.
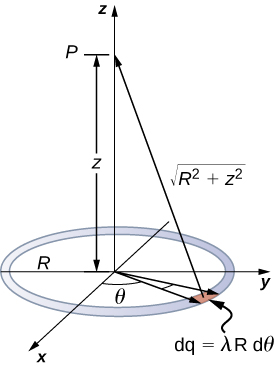
Estrategia
Usamos el mismo procedimiento que para el cable cargado. La diferencia aquí es que la carga se distribuye en un círculo. Dividimos el círculo en elementos infinitesimales formados como arcos en el círculo y usamos las coordenadas cilíndricas que se muestran en la .
Solución
Un elemento general del arco entre $θ$ y $θ + dθ$ es de longitud $Rdθ$ y, por lo tanto, contiene una carga igual a $λRdθ$. El elemento está a una distancia $\sqrt{z^2 + R^2}$ de $P$, y por lo tanto el potencial es
$$\begin{split} V_P &= k \int \frac{dq}{r} = k \int_0^{2π} \frac{λRdθ}{\sqrt{z^2 + R^2}} = \frac{kλR}{\sqrt{z^2 + R^2}} \int_0^{2π} dθ \\ &= \frac{2πkλR}{\sqrt{z^2 + R^2}} = k \frac{q_{\textsf{tot}}}{\sqrt{z^2 + R^2}} \end{split}$$Explicación
Este resultado es esperado porque cada elemento del anillo está a la misma distancia del punto $P$. El potencial neto en $P$ es el de la carga total colocada a la distancia común, $\sqrt{z^2 + R^2}$.
Ejemplo 7.14
Potencial debido a un disco de carga uniforme
Un disco de radio $R$ tiene una densidad de carga uniforme $σ$, con unidades de culombio metro al cuadrado. Encuentra el potencial eléctrico en cualquier punto del eje que pasa por el centro del disco.
Estrategia
Dividimos el disco en celdas con forma de anillo, y utilizamos el resultado para un anillo resuelto en el ejemplo anterior, luego integramos sobre $r$ además de $θ$. Esto se muestra en la .
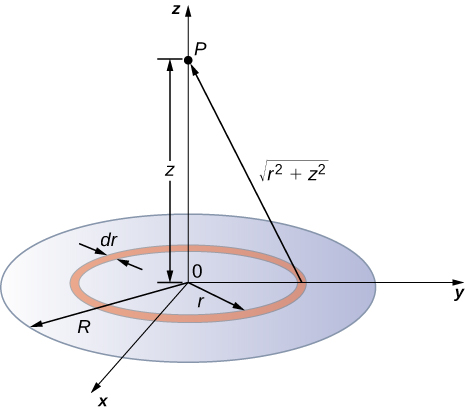
Solución
Una celda de ancho infinitesimal entre las coordenadas cilíndricas $r$ y $r + dr$ que se muestra en la será un anillo de cargas cuyo potencial eléctrico $dV_P$ en el punto de campo tiene la siguiente expresión
$$dV_P = k\frac{dq}{\sqrt{z^2 + R^2}}$$donde
$$dq = σ2πrdr$$La superposición de potencial de todos los anillos infinitesimales que componen el disco da el potencial neto en el punto $P$. Esto se logra al integrar desde $r = 0$ a $r = R$:
Explicación
El procedimiento básico es integrar primero alrededor de $θ$ y luego sobre $r$. Ya se ha demostrado para una densidad de carga uniforme (constante). A menudo, la densidad de carga variará con $r$, y luego la última integral dará resultados diferentes.
Ejemplo 7.15
Potencial debido a un cable infinito cargado
Encuentra el potencial eléctrico debido a un cable infinitamente largo y uniformemente cargado.
Estrategia
Como ya hemos calculado el potencial de un cable finito de longitud $L$ en el ejemplo 7.7, podríamos preguntarnos si tomar $L → ∞$ en nuestro resultado anterior funcionará:
$$V_P = \lim_{l→∞} kλln \left(\frac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}} \right)$$Sin embargo, este límite no existe porque el argumento del logaritmo se convierte en $[2/0]$ como $L → ∞$, por lo que esta forma de encontrar $V$ de un cable infinito no funciona. La razón de este problema puede deberse al hecho de que las cargas no están localizadas en algún espacio, sino que continúan hasta el infinito en la dirección del cable.
Por lo tanto, nuestra suposición (tácita) de que el potencial cero debe estar a una distancia infinita del cable ya no es válida.
Para evitar esta dificultad al calcular los límites, usemos la definición de potencial integrando el campo eléctrico de la sección anterior y el valor del campo eléctrico de esta configuración de carga del capítulo anterior.
Solución
Usamos la integral
$$V_P = -\int_P^R \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$$donde $R$ es una distancia finita desde la línea de carga, como se muestra en la .
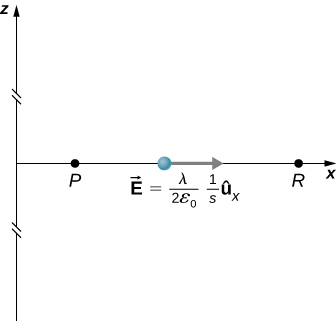
Con esta configuración, usamos $\overrightarrow{\bold{E}}_P = 2kλ\frac{1}{s}\^{s}$ y $d\overrightarrow{\bold{l}} = d\overrightarrow{\bold{s}}$ para obtener
$$V_P - V_R = -\int_P^R kλ\frac{1}{s}ds = -2kλln\frac{s_P}{s_R}$$Ahora, si definimos el potencial de referencia $V_R = 0$ en $s_R = 1 m$, esto se simplifica a
$$V_P = -2kλlns_P$$Observa que esta forma de potencial es bastante útil; es $0$ a $1 m$ y no está definido en infinito, por lo que no podemos utilizar este último como referencia.
Explicación
Aunque calcular el potencial directamente puede ser muy conveniente, acabamos de encontrar un sistema para el cual esta estrategia no funciona bien. En tales casos, volver a la definición de potencial en términos del campo eléctrico puede ofrecer un camino a seguir.
 Comprueba tu aprendizaje 7.10
Comprueba tu aprendizaje 7.10
Recordemos que, en ciertos sistemas, pudimos calcular el potencial integrándolo en el campo eléctrico. Como ya puedes sospechar, esto significa que podemos calcular el campo eléctrico tomando derivadas del potencial, aunque pasar de una cantidad escalar a una vectorial introduce algunas arrugas interesantes. Con frecuencia necesitamos $\overrightarrow{\bold{E}}$ para calcular la fuerza en un sistema; dado que a menudo es más sencillo calcular el potencial directamente, existen sistemas en los que es útil calcular $V$ y luego derivar $\overrightarrow{\bold{E}}$ a partir de él.
En general, independientemente de si el campo eléctrico es uniforme, apunta en la dirección del potencial decreciente, porque la fuerza en una carga positiva está en la dirección de $\overrightarrow{\bold{E}}$ y también en la dirección del potencial $V$ más bajo. Además, la magnitud de $\overrightarrow{\bold{E}}$ es igual a la tasa de disminución de $V$ con la distancia. Cuanto más rápido $V$ disminuye a lo largo de la distancia, mayor es el campo eléctrico. Esto nos da el siguiente resultado.
Relación entre el voltaje y el campo eléctrico uniforme
La relación entre el voltaje y el campo eléctrico uniforme es
$$E = -\frac{ΔV}{Δs}$$donde $Δs$ es la distancia sobre la cual tiene lugar el cambio en el potencial $ΔV$. El signo menos nos dice que $E$ apunta en la dirección del potencial decreciente. Se dice que el campo eléctrico es el gradiente (como en grado o pendiente) del potencial eléctrico.
Para potenciales continuamente cambiantes, $ΔV$ y $Δs$ se vuelven infinitesimales, y necesitamos el cálculo diferencial para determinar el campo eléctrico. Como se muestra en la , si tratamos la distancia $Δs$ como muy pequeña para que el campo eléctrico sea esencialmente constante sobre ella, encontramos que
$$E_s = -\frac{dV}{ds}$$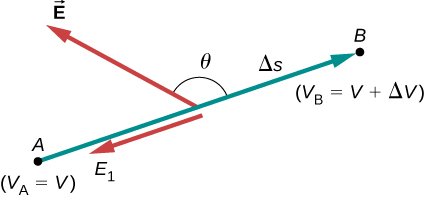
por lo tanto, los componentes del campo eléctrico en las direcciones cartesianas están dados por
Esto nos permite definir el operador vectorial "grad" o "nabla", que nos permite calcular el gradiente en un solo paso. En coordenadas cartesianas, toma la forma
Con esta notación, podemos calcular el campo eléctrico del potencial con
un proceso que llamamos calcular el gradiente del potencial.
Si tenemos un sistema con simetría cilíndrica o esférica, solo necesitamos usar el operador nabla en las coordenadas apropiadas:
Ejemplo 7.17
Campo eléctrico de una carga puntual
Calcula el campo eléctrico de una carga puntual desde el potencial.
Estrategia
Se sabe que el potencial es $V = k\frac{q}{r}$, que tiene una simetría esférica. Por lo tanto, usamos el operador esférico de la fórmula $\overrightarrow{\bold{E}} = -\overrightarrow{∇}V$.
Solución
Realizar este cálculo nos da
$$\begin{split} \overrightarrow{\bold{E}} &= - \left(\^{r}\frac{∂}{∂r} + \^{θ}\frac{1}{r} \frac{∂}{∂θ} + \^{φ}\frac{1}{rsenθ} \frac{∂}{∂φ} \right) k\frac{q}{r} \\ &= -kq \left(\^{r} \frac{∂}{∂r} \frac{1}{r} + \^{θ} \frac{1}{r} \frac{1}{r} \frac{∂}{∂θ} + \^{φ} \frac{1}{rsenθ} \frac{∂}{∂φ} \frac{1}{r} \right) \end{split}$$Esta ecuación se simplifica a
$$\overrightarrow{\bold{E}} = -kq \left(\^{r}\frac{-1}{r^2} + \^{θ}0 + \^{φ}0 \right) = k\frac{q}{r^2}\^{r}$$tal como lo esperábamos
Explicación
No solo obtuvimos la ecuación para el campo eléctrico de una partícula puntual que hemos visto antes, también tenemos una demostración de que $\overrightarrow{\bold{E}}$ apunta en la dirección del potencial decreciente, como se muestra en la .
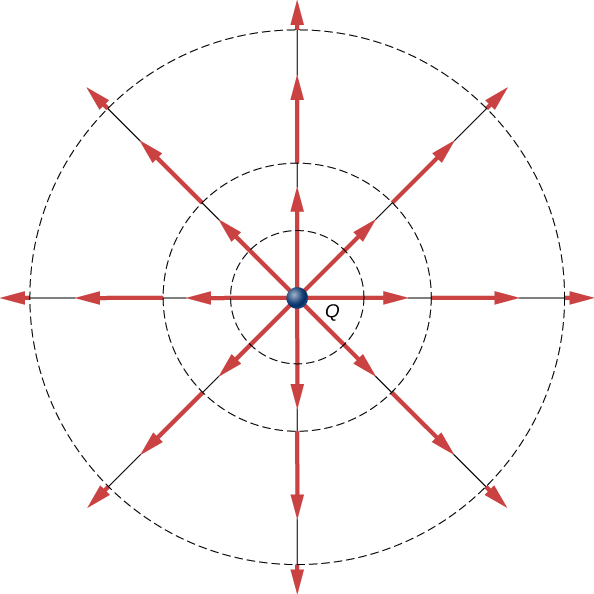
Ejemplo 7.18
Campo eléctrico de un anillo de carga
Usa el potencial encontrado en el Ejemplo 7.8 para calcular el campo eléctrico a lo largo del eje de un anillo de carga ().
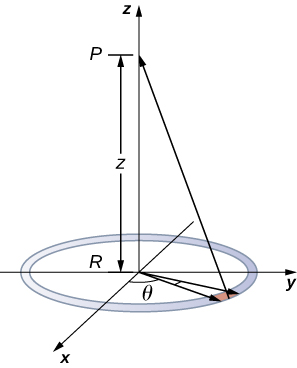
Estrategia
En este caso, solo estamos interesados en una dimensión, el eje $z$.
Por lo tanto, usamos $E_z = -\frac{∂V}{∂z}$, con el potencial $V = k\frac{q_{\textsf{tot}}}{\sqrt{z^2 + R^2}}$ encontrado previamente.
Solución
Tomando la derivada
$$E_z = -\frac{∂}{∂z}\frac{q_{\textsf{tot}}}{\sqrt{z^2 + R^2}} = k\frac{q_{\textsf{tot}}z}{(z^2 + R^2)^{3/2}}$$Explicación
De nuevo, esto coincide con la ecuación para el campo eléctrico encontrado previamente. También demuestra un sistema en el que no es necesario utilizar el operador nabla completo.
 Comprueba tu aprendizaje 7.11
Comprueba tu aprendizaje 7.11
Podemos representar potenciales eléctricos (voltajes) pictóricamente, tal como dibujamos para ilustrar campos eléctricos. Esto no es sorprendente, ya que los dos conceptos están relacionados. Considera la Figura 7.30, que muestra una carga puntual positiva aislada y sus líneas de campo eléctrico, que irradian desde una carga positiva y terminan con cargas negativas. Usamos flechas rojas para representar la magnitud y dirección del campo eléctrico, y usamos líneas negras para representar lugares donde el potencial eléctrico es constante. Estas se denominan superficies equipotenciales en tres dimensiones o líneas equipotenciales en dos dimensiones. El término equipotencial también se usa como sustantivo, refiriéndose a una línea o superficie equipotencial. El potencial de una carga puntual es el mismo en cualquier parte de una esfera imaginaria de radio r que rodea la carga. Esto es cierto porque el potencial para una carga puntual viene dado por $V = kq/r$ y, por lo tanto, tiene el mismo valor en cualquier punto que sea una distancia dada r de la carga. Una esfera equipotencial es un círculo en la vista bidimensional de la . Debido a que las líneas del campo eléctrico apuntan radialmente lejos de la carga, son perpendiculares a las líneas equipotenciales.
Es importante tener en cuenta que las líneas equipotenciales son siempre perpendiculares a las líneas de campo eléctrico. No se requiere ningún trabajo para mover una carga a lo largo de una equipotencial, ya que $ΔV = 0$. Por lo tanto, el trabajo es
$$W = -ΔU = -qΔV = 0$$El trabajo es cero si la dirección de la fuerza es perpendicular al desplazamiento.
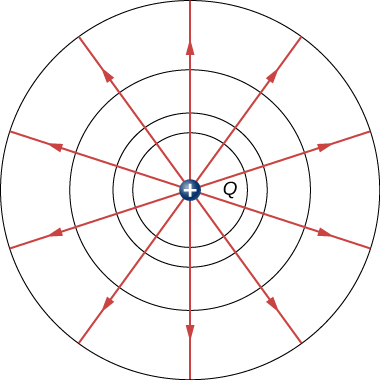
La fuerza está en la misma dirección que $E$, por lo que el movimiento a lo largo de un equipotencial debe ser perpendicular a $E$. Más precisamente, el trabajo está relacionado con el campo eléctrico mediante
$$W = \overrightarrow{\bold{F}} \cdot \overrightarrow{\bold{r}} = q\overrightarrow{\bold{E}} \cdot \overrightarrow{\bold{r}} = qEdcosθ = 0$$Observa que en esta ecuación, $E$ y $F$ simbolizan las magnitudes del campo eléctrico y la fuerza, respectivamente.
Ni $q$ ni $E$ son cero; $d$ tampoco es cero. Entonces $cosθ$ debe ser $0$, lo que significa que $θ$ debe ser $90°$. En otras palabras, el movimiento a lo largo de un equipotencial es perpendicular a $E$.
Una de las reglas para los campos y conductores eléctricos estáticos es que el campo eléctrico debe ser perpendicular a la superficie de cualquier conductor. Esto implica que un conductor es una superficie equipotencial en situaciones estáticas. No puede haber diferencia de voltaje en la superficie de un conductor, o las cargas fluirán. Uno de los usos de este hecho es que un conductor se puede fijar a lo que consideramos cero voltios conectándolo a la tierra con un buen conductor, un proceso llamado conexión a tierra. La conexión a tierra puede ser una herramienta de seguridad útil. Por ejemplo, conectar a tierra la carcasa de metal de un aparato eléctrico garantiza que esté a cero voltios con respecto a la Tierra.
Como un conductor es un equipotencial, puede reemplazar cualquier superficie equipotencial. Por ejemplo, en la , un conductor esférico cargado puede reemplazar la carga puntual, y el campo eléctrico y las superficies potenciales fuera de él no se modificarán, lo que confirma la afirmación de que una distribución de carga esférica es equivalente a una carga puntual en su centro.
La figura muestra el campo eléctrico y las líneas equipotenciales para dos cargas iguales y opuestas. Dadas las líneas de campo eléctrico, las líneas equipotenciales se pueden dibujar simplemente haciéndolas perpendiculares a las líneas del campo eléctrico. Por el contrario, dadas las líneas equipotenciales, como en la figura (a), las líneas del campo eléctrico se pueden dibujar haciéndolas perpendiculares a los equipotenciales, como en la figura (b).
La siguiente escena interactiva, diseñada por Christian Wolfgang, muestra el potencial de múltiples cargas puntuales. Usa los botones para agregar cargas y arrástralas para crear varias configuraciones. El potencial en un punto es igual al trabajo realizado por un agente externo para llevar una unidad de carga positiva desde el infinito hasta ese punto sin ninguna aceleración. Las regiones donde el potencial es positivo se muestran en rojo y las regiones donde el potencial es negativo se muestran en azul.
El valor exacto del potencial $U$ se muestra en un cuadro de mensaje amarillo. La superficie sobre la cual el potencial eléctrico tiene un valor igual en todas partes se denomina superficie equipotencial. Se muestra como una línea blanca (contorno) en nuestro modelo bidimensional.
La siguiente escena interactiva, diseñada por Pance Cavkovski, muestra un campo eléctrico creado por múltiples cargas puntuales o esferas, que se puede calcular como una superposición de los vectores de fuerza eléctrica individuales. El potencial eléctrico nuevamente puede calcularse con superposición, excepto que es un valor escalar, no uno vectorial. El conjunto de puntos que tienen el mismo potencial, crean una superficie equipotencial. Cada vector de fuerza es normal a la superficie equipotencial en el mismo punto.Haz clic en el botón para otras configuraciones de carga, arrastra las cargas y, para un mejor análisis, haz clic en el botón de ampliar la escena.
Para mejorar tu intuición, mostramos una variante tridimensional del potencial en un sistema con dos cargas opuestas. La muestra un mapa tridimensional del potencial eléctrico, donde las líneas en el mapa son para superficies equipotenciales. La colina tiene carga positiva y la depresión tiene carga negativa. El potencial es cero lejos de las cargas. Ten en cuenta que el corte en un potencial particular implica que las cargas están en esferas conductoras con un radio finito.
En la se muestra un mapa bidimensional del plano transversal que contiene ambas cargas. La línea que es equidistante de las dos cargas opuestas corresponde al potencial cero, ya que en los puntos en la línea, el potencial positivo de la carga positiva cancela el potencial negativo de la carga negativa. Las líneas equipotenciales en el plano transversal son circuitos cerrados, que no son necesariamente círculos, ya que en cada punto, el potencial neto es la suma de los potenciales de cada carga.
Uno de los casos más importantes es el de las placas conductoras paralelas familiares que se muestran en la . Entre las placas, los equipotenciales están espaciados uniformemente y son paralelos. El mismo campo podría mantenerse colocando placas conductoras en las líneas equipotenciales a los potenciales mostrados.
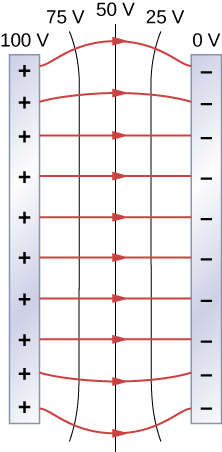
Considera las placas paralelas en la . Estos tienen líneas equipotenciales que son paralelas a las placas entre en el espacio y espaciadas uniformemente. Un ejemplo de esto (con valores de muestra) se da en la . Podríamos dibujar un conjunto similar de isolíneas equipotenciales para la gravedad en la colina que se muestra en la . Si la colina tiene algún grado en la misma pendiente, las isolíneas a lo largo de esa extensión serían paralelas entre sí. Además, en regiones de pendiente constante, las isolíneas estarían espaciadas uniformemente. Un ejemplo de líneas topográficas reales se muestra en la .
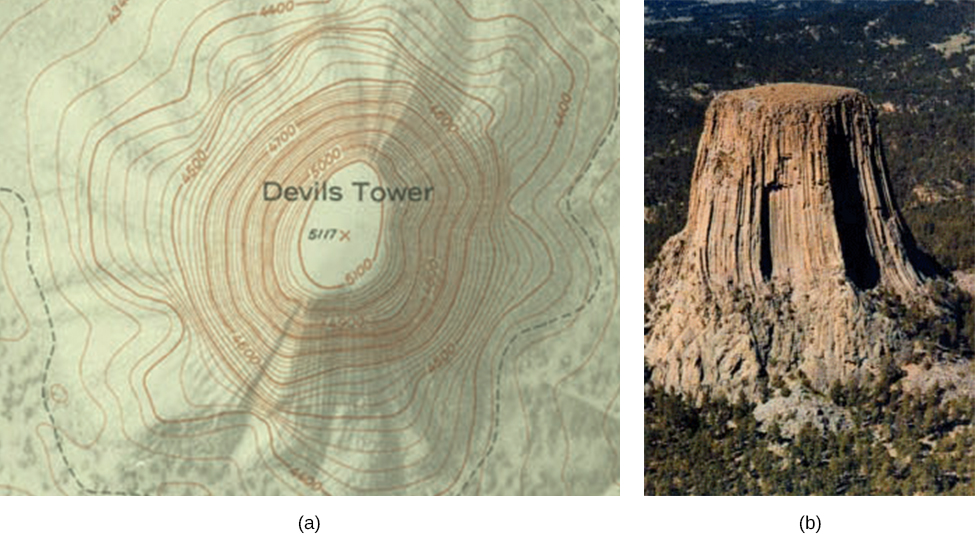
Ejemplo 7.19
Cálculo de líneas equipotenciales
Has visto las líneas equipotenciales de una carga puntual en la . ¿Cómo los calculamos? Por ejemplo, si tenemos una carga $+ 10 nC$ en el origen, ¿cuáles son las superficies equipotenciales en las que el potencial es (a) $100 V$, (b) $50 V$, (c) $20 V$ y (d) $10 V$?
Estrategia
La ecuación para el potencial de una carga puntual es una constante, resuelve para la(s) variable(s) restante(s). Luego calcula los valores según sea necesario.
Solución
En $V = k\dfrac{q}{r}$, sea $V$ una constante. La única variable restante es $r$; por lo tanto, $r = kqV = constante$. Por lo tanto, las superficies equipotenciales son esferas sobre el origen. Sus ubicaciones son:
a. $r = k\dfrac{q}{V} = (8.99 × 10^9 Nm^2/C^2)\dfrac{10 × 10^{-9} C}{100 V} = 0.90 m$
b. $r = k\dfrac{q}{V} = (8.99 × 10^9 Nm^2/C^2)\dfrac{10 × 10^{-9} C}{50 V} = 1.8 m$
c. $r = k\dfrac{q}{V} = (8.99 × 10^9 Nm^2/C^2)\dfrac{10 × 10^{-9} C}{20 V} = 4.5 m$
d. $r = k\dfrac{q}{V} = (8.99 × 10^9 Nm^2/C^2)\dfrac{10 × 10^{-9} C}{10 V} = 9.0 m$
Explicación
Las superficies equipotenciales alrededor de una carga puntual son esferas de radio constante, como se mostró anteriormente, con ubicaciones bien definidas.
Ejemplo 7.20
Diferencia de potencial entre placas paralelas con carga opuesta
Dos grandes placas conductoras tienen cargas iguales y opuestas, con una densidad de carga superficial $σ$ de magnitud $6,81 × 10 ^{-7} C/m^2$, como se muestra en la . La separación entre las placas es $l = 6,50 mm$. (a) ¿Cuál es el campo eléctrico entre las placas? (b) ¿Cuál es la diferencia de potencial entre las placas? (c) ¿Cuál es la distancia entre los planos equipotenciales que difieren en $100 V$?
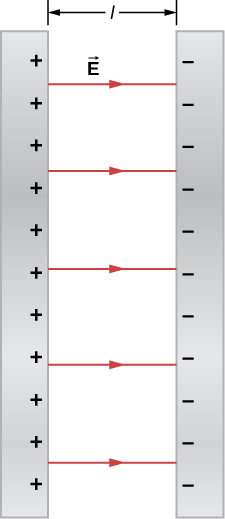
Estrategia
(a) Dado que las placas se describen como "grandes" y la distancia entre ellas no lo es, aproximaremos cada una de ellas como un plano infinito, y aplicaremos el resultado de la ley de Gauss del capítulo anterior.
(b) Utiliza $ΔV_{AB} = -\int_A^B \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}$.
(c) Dado que el campo eléctrico es constante, encuentra la relación de $100 V$ a la diferencia de potencial total; luego calcula esta fracción de la distancia.
Solución
(a) El campo eléctrico se dirige desde la placa positiva a la negativa como se muestra en la figura, y su magnitud viene dada por
$$E = \frac{σ}{ε_0} = \frac{6.81 × 10^{−7} C/m^2}{8.85 × 10^{−12} C^2/N \cdot m^2} = 7.69 × 10^4 V/m.$$(b) Para encontrar la diferencia de potencial $ΔV$ entre las placas, usamos una ruta de la placa negativa a la positiva que se dirige contra el campo. El vector de desplazamiento $d\overrightarrow{\bold{l}}$ y el campo eléctrico $\overrightarrow{\bold{E}}$ son antiparalelos, por lo que $\overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}} = -Edl$. La diferencia de potencial entre la placa positiva y la placa negativa es entonces
(c) La diferencia de potencial total es de $500 V$, por lo que $1/5$ de la distancia entre las placas será la distancia entre las diferencias de potencial de $100 V$. La distancia entre las placas es de $6,5 mm$, por lo que habrá $1,3 mm$ entre las diferencias de potencial de $100 V$.
Explicación
Ahora has visto un cálculo numérico de las ubicaciones de los equipotenciales entre dos placas paralelas cargadas.
 Comprueba tu aprendizaje 7.12
Comprueba tu aprendizaje 7.12
En el ejemplo 7.19 con una carga puntual, encontramos que las superficies equipotenciales estaban en forma de esferas, con la carga puntual en el centro. Dado que una esfera conductora en equilibrio electrostático es una superficie esférica equipotencial, deberíamos esperar que pudiéramos reemplazar una de las superficies en el Ejemplo 7.19 con una esfera conductora y tener una solución idéntica fuera de la esfera. Sin embargo, por dentro será bastante diferente.
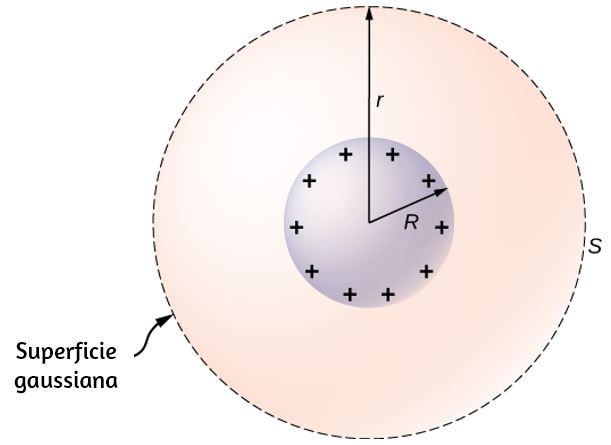
Para investigar esto, considera la esfera de conducción aislada de la que tiene un radio $R$ y una carga excedente $q$. Para encontrar el campo eléctrico tanto dentro como fuera de la esfera, ten en cuenta que la esfera está aislada, por lo que su distribución de cambio de superficie y el campo eléctrico de esa distribución son esféricamente simétricos. Por lo tanto, podemos representar el campo como $\overrightarrow{\bold{E}} = E(r)\^{r}$. Para calcular $E(r)$, aplicamos la ley de Gauss sobre una superficie esférica cerrada S de radio r que es concéntrica con la esfera conductora. Como $r$ es constante y $\^{n} = \^{r}$ en la esfera,
Para $r < R$, $S$ está dentro del conductor, recuerda de nuestro estudio previo de la ley de Gauss que $q_{\textsf{enc}} = 0$ y la ley de Gauss da $E(r) = 0$, como se esperaba dentro de un conductor en equilibrio. Si $r > R$, $S$ encierra el conductor de modo que $q_{\textsf{enc}} = q$. De la ley de Gauss,
$$E(r)4πr^2 = \frac{q}{ε_0}$$El campo eléctrico de la esfera, por lo tanto, puede escribirse como
$$E = 0 \; \textsf{ para } \; r < 0$$ $$E = \frac{1}{4πε_0}\frac{q}{r^2}\^{r} \; \textsf{ para } \; r ≥ 0$$Como se esperaba, en la región $r ≥ R$, el campo eléctrico debido a una carga $q$ colocada en una esfera conductora aislada de radio $R$ es idéntico al campo eléctrico de una carga puntual $q$ situada en el centro de la esfera.
Para encontrar el potencial eléctrico dentro y fuera de la esfera, ten en cuenta que para $r ≥ R$, el potencial debe ser el mismo que el de una carga puntual aislada $q$ ubicada en $r = 0$,
$$V(r) = \frac{1}{4πε_0}\frac{q}{r} (r ≥ R)$$debido a la similitud del campo eléctrico.
Para $r < R$, $E = 0$, entonces $V(r)$ es constante en esta región. Desde $V(R) = q/4πε_0R$,
Usaremos este resultado para mostrar que
$$σ_1R_1 = σ_2R_2$$para dos esferas conductoras de radios $R_1$ y $R_2$, con densidades de carga superficial $σ_1$ y $σ_2$ respectivamente, que están conectadas por un cable delgado, como se muestra en la . Las esferas están suficientemente separadas para que cada una se pueda tratar como si estuviera aislada (aparte del cable). Ten en cuenta que la conexión por el cable significa que todo este sistema debe ser un equipotencial.

Acabamos de ver que el potencial eléctrico en la superficie de una esfera conductora con carga y aislada de radio $R$ es
$$V = \frac{1}{4πε_0}\frac{q}{R}$$Ahora, las esferas están conectadas por un conductor y por lo tanto tienen el mismo potencial; entonces
$$\frac{1}{4πε_0}\frac{q_1}{R_1} = \frac{1}{4πε_0}\frac{q_2}{R_2}$$y
$$\frac{q_1}{R_1} = \frac{q_2}{R_2}$$La carga neta en una esfera conductora y su densidad de carga superficial están relacionadas por $q = σ(4πR^2)$. Sustituyendo esta ecuación en la anterior, encontramos
$$σ_1R_1 = σ_2R_2$$Obviamente, dos esferas conectadas por un cable delgado no constituyen un conductor típico con un radio de curvatura variable.
Sin embargo, este resultado al menos proporciona una idea cualitativa de cómo la densidad de carga varía en la superficie de un conductor. La ecuación indica que cuando el radio de curvatura es grande (los puntos $B$ y $D$ en la ), $σ$ y $E$ son pequeños.
De forma similar, las cargas tienden a ser más densas cuando la curvatura de la superficie es mayor, como lo demuestra la distribución de carga en el metal de forma extraña (). La densidad de carga superficial es más alta en ubicaciones con un pequeño radio de curvatura que en ubicaciones con un gran radio de curvatura.
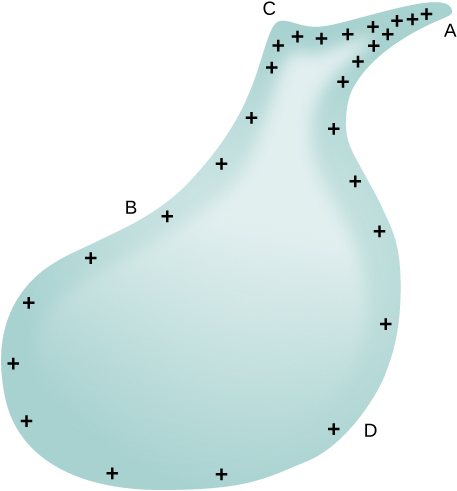
Una aplicación práctica de este fenómeno es el pararrayos, que es simplemente una varilla de metal puesta a tierra con un extremo afilado apuntando hacia arriba. A medida que la carga positiva se acumula en el suelo debido a una nube cargada negativamente, el campo eléctrico alrededor del punto agudo se hace muy grande. Cuando el campo alcanza un valor de aproximadamente $3,0 × 10^6 N/C$ (la fuerza dieléctrica del aire), los iones libres en el aire se aceleran a energías tan altas que sus colisiones con las moléculas de aire realmente ionizan las moléculas. Los electrones libres resultantes en el aire fluyen a través de la varilla hacia la Tierra, neutralizando así parte de la carga positiva. Esto evita que el campo eléctrico entre la nube y el suelo sea lo suficientemente grande como para producir un rayo en la región alrededor de la barra.
Una aplicación importante de campos eléctricos y líneas equipotenciales implica el corazón. El corazón se basa en señales eléctricas para mantener su ritmo. El movimiento de las señales eléctricas hace que las cámaras del corazón se contraigan y relajen. Cuando una persona tiene un ataque al corazón, el movimiento de estas señales eléctricas puede verse alterado. Se puede usar un marcapasos artificial y un desfibrilador para iniciar el ritmo de las señales eléctricas. Las líneas equipotenciales alrededor del corazón, la región torácica y el eje del corazón son formas útiles de controlar la estructura y las funciones del corazón. Un electrocardiograma (ECG) mide las pequeñas señales eléctricas que se generan durante la actividad del corazón.
Finalmente, retomamos la escena interactiva de PhET Simulaciones, para que muevas las cargas positivas y negativas y observes el campo eléctrico y el potencial eléctrico. Traza líneas equipotenciales, crea modelos de dipolos, condensadores, etcétera.
El estudio de la electrostática ha demostrado ser útil en muchas áreas. Este módulo cubre solo algunas de las muchas aplicaciones de electrostática.
Los generadores Van de Graaff (o Van de Graaffs) no solo son dispositivos espectaculares que se utilizan para demostrar el alto voltaje debido a la electricidad estática, sino que también se utilizan para investigaciones serias. El primero fue construido por Robert Van de Graaff en 1931 (basado en las sugerencias originales de Lord Kelvin) para su uso en la investigación de la física nuclear. La muestra un esquema de una gran versión de la investigación. Van de Graaffs utiliza superficies lisas y puntiagudas, y conductores y aisladores para generar grandes cargas estáticas y, por lo tanto, grandes voltajes.
Se puede depositar una carga excesiva muy grande en la esfera porque se mueve rápidamente hacia la superficie externa. Los límites prácticos surgen porque los grandes campos eléctricos se polarizan y eventualmente ionizan los materiales circundantes, creando cargas libres que neutralizan el exceso de carga o permiten que escape. Sin embargo, los voltajes de 15 millones de voltios están dentro de los límites prácticos.
En el vídeo que se presenta a continuación y publicado por Massachusetts Institute of Technology, un papel confeti se coloca encima de un generador Van de Graaff y sale volando cuando se quita la varilla de conexión a tierra.
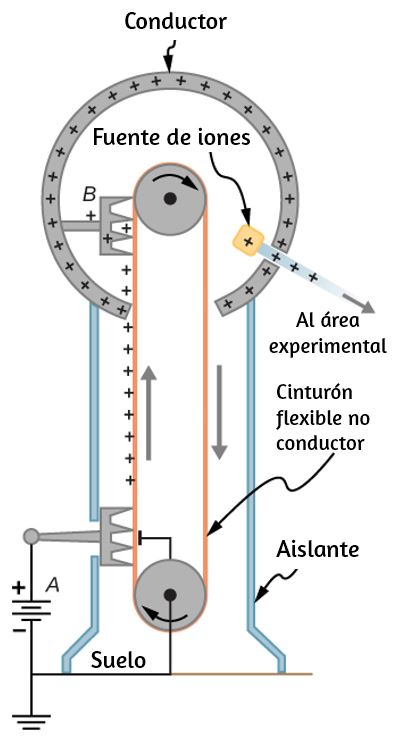
La mayoría de las fotocopiadoras usan un proceso electrostático llamado xerografía, una palabra acuñada de las palabras griegas xeros para seco y graphos para escritura. El corazón del proceso se muestra en forma simplificada en la .
Un tambor de aluminio recubierto de selenio se rocía con carga positiva desde los puntos en un dispositivo llamado corotrón. El selenio es una sustancia con una propiedad interesante: es un fotoconductor. Es decir, el selenio es un aislante en la oscuridad y un conductor cuando se expone a la luz.
En la primera etapa del proceso de xerografía, el tambor de aluminio conductor se conecta a tierra de modo que se induce una carga negativa debajo de la capa delgada de selenio uniformemente cargado positivamente.
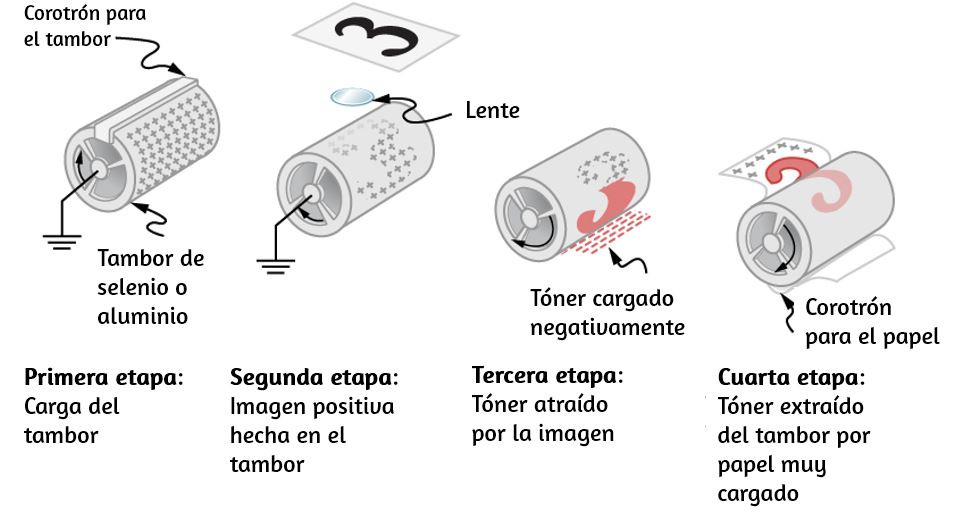
En la segunda etapa, la superficie del tambor está expuesta a la imagen de lo que se va a copiar. En lugares donde la imagen es clara, el selenio se vuelve conductor y la carga positiva se neutraliza. En áreas oscuras, la carga positiva permanece, por lo que la imagen se ha transferido al tambor.
La tercera etapa toma un polvo negro seco, llamado tóner, y lo rocía con una carga negativa para atraerlo a las regiones positivas del tambor. A continuación, una hoja de papel en blanco recibe una carga positiva mayor que en el tambor, de modo que extraerá el tóner del tambor. Finalmente, el papel y el tóner contenido electrostáticamente se pasan a través de rodillos de presión calentados, que funden y adhieren permanentemente el tóner a las fibras del papel.
Las impresoras láser utilizan el proceso xerográfico para crear imágenes de alta calidad en papel, empleando un láser para producir una imagen en el tambor fotoconductor como se muestra en la . En su aplicación más común, la impresora láser recibe una salida de una computadora y puede lograr un resultado de alta calidad debido a la precisión con la que se puede controlar la luz láser. Muchas impresoras láser realizan un procesamiento de información significativo, como la creación de letras o fuentes sofisticadas, y en el pasado pueden haber contenido una computadora más poderosa que la que les proporciona los datos brutos que se van a imprimir.
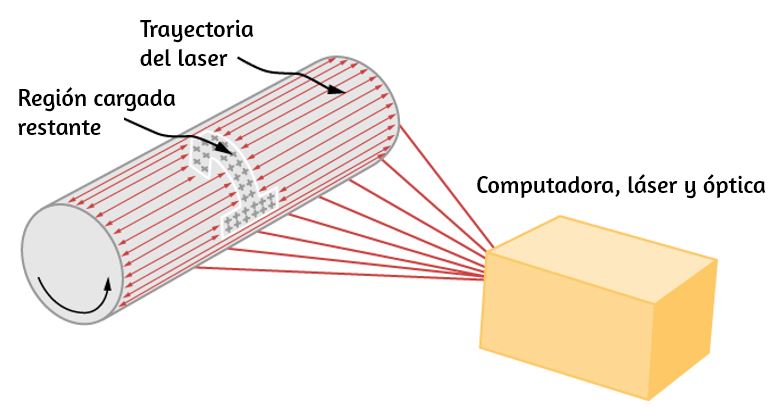
La impresora de chorro de tinta, comúnmente utilizada para imprimir texto y gráficos generados por computadora, también emplea electrostática. Una boquilla produce una fina pulverización de diminutas gotas de tinta, a las que luego se les aplica una carga electrostática ().
Una vez cargadas, las gotitas se pueden dirigir, utilizando pares de placas cargadas, con gran precisión para formar letras e imágenes en papel. Las impresoras de inyección de tinta pueden producir imágenes en color utilizando un chorro negro y otros tres chorros con colores primarios, generalmente cian, magenta y amarillo, de forma similar a como un televisor a color produce color (esto es más difícil con la xerografía, que requiere múltiples tambores y tóneres).
La pintura electrostática emplea carga electrostática para pulverizar pintura en superficies de formas extrañas. La repulsión mutua de cargas similares hace que la pintura salga volando de su fuente.
La tensión superficial forma gotas, que luego son atraídas por cargas diferentes a la superficie que se va a pintar. La pintura electrostática puede llegar a lugares difíciles de alcanzar, aplicando una capa uniforme de manera controlada. Si el objeto es un conductor, el campo eléctrico es perpendicular a la superficie, tendiendo a colocar las gotas en forma perpendicular. Las esquinas y los puntos en los conductores recibirán pintura adicional.
Otra aplicación importante de la electrostática se encuentra en los limpiadores de aire, grandes y pequeños. La parte electrostática del proceso coloca una carga excesiva (generalmente positiva) sobre el humo, polvo, polen y otras partículas en el aire y luego pasa el aire a través de una rejilla con carga opuesta que atrae y retiene las partículas cargadas ()

Los precipitadores electrostáticos grandes se usan industrialmente para eliminar más del $99$% de las partículas de las emisiones de gases de chimenea asociadas con la quema de carbón y petróleo. Los precipitadores caseros, a menudo junto con el sistema de calefacción y aire acondicionado del hogar, son muy efectivos en la eliminación de partículas contaminantes, irritantes y alérgenos.

En la siguiente página, como cierre de este capítulo, presentamos una escena interactiva, diseñada por Dev Ramtal y Adrian Dobre, en la que aparecen varias cargas aleatorias (positivas y negativas) y unas partículas cargadas que se desplazan según el campo eléctrico que la estén afectando.

Los condensadores (también conocido frecuentemente con el anglicismo capacitor) son componentes importantes de los circuitos eléctricos en muchos dispositivos electrónicos, incluidos marcapasos, teléfonos celulares y computadoras. En este capítulo, estudiamos sus propiedades y, en los siguientes capítulos, examinamos su función en combinación con otros elementos del circuito. Por sí solos, los condensadores a menudo se usan para almacenar energía eléctrica y liberarla cuando sea necesario.
Con otros componentes del circuito, los condensadores a menudo actúan como parte de un filtro que permite que algunas señales eléctricas pasen y bloqueen otras. Puedes ver por qué los condensadores se consideran como uno de los componentes fundamentales de los circuitos eléctricos.
Un condensador es un dispositivo utilizado para almacenar carga eléctrica y energía eléctrica. Consiste en al menos dos conductores eléctricos separados por una distancia (Ten en cuenta que tales conductores eléctricos a veces se denominan "electrodos", pero más correctamente, son "placas de capacitores"). El espacio entre los condensadores puede ser simplemente un vacío, y, en ese caso, un condensador se conoce entonces como "Condensador de vacío". Sin embargo, el espacio generalmente se llena con un material aislante conocido como dieléctrico. La cantidad de almacenamiento en un condensador está determinada por una propiedad llamada capacitancia, que aprenderás más adelante un poco más adelante en esta sección.
Los condensadores tienen aplicaciones que van desde la filtración de la estática de la recepción de radio hasta el almacenamiento de energía en desfibriladores de corazón. Por lo general, los condensadores comerciales tienen dos partes conductoras cerca unas de otras pero sin tocar, como las de la . La mayoría de las veces, se usa un dieléctrico entre las dos placas. Cuando los terminales de la batería están conectados a un condensador inicialmente descargado, el potencial de la batería mueve una pequeña cantidad de carga de magnitud $Q$ desde la placa positiva a la placa negativa. El condensador permanece neutral en general, pero con cargas $+Q$ y $-Q$ que residen en placas opuestas.
Un sistema compuesto por dos placas idénticas de conducción en paralelo separadas por una distancia se denomina condensador de placa paralela ().
La magnitud del campo eléctrico en el espacio entre las placas paralelas es $E = σ/ε_00$, donde $σ$ denota la densidad de carga superficial en una placa (recuerde que $σ$ es la carga $Q$ por área de superficie $A$). Por lo tanto, la magnitud del campo es directamente proporcional a $Q$.
Los condensadores con diferentes características físicas (como la forma y el tamaño de sus placas) almacenan diferentes cantidades de carga para el mismo voltaje $V$ aplicado a través de sus placas. La capacitancia $C$ de un condensador se define como la relación de la carga máxima $Q$ que puede almacenarse en un condensador a la tensión aplicada $V$ a través de sus placas. En otras palabras, la capacidad es la mayor cantidad de carga por voltio que se puede almacenar en el dispositivo:
La unidad de capacitancia en el SI es el faradio ($F$), llamado así por Michael Faraday (1791-1867). Como la capacitancia es la carga por unidad de voltaje, un faradio es un culombio por cada voltio, o
$$1 F\frac{1 C}{1 V}$$Por definición, un condensador de $1.0 F$ puede almacenar $1.0 C$ de carga (una cantidad muy grande de carga) cuando la diferencia de potencial entre sus placas es solo $1.0 V$. Un faradio es por lo tanto una capacitancia muy grande. Los valores típicos de capacitancia van desde picofaradios ($1pF = 10^{-12} F$) hasta milifaradios ($1mF = 10^{-3} F$), que también incluyen microfaradios ($1μF = 10^{-6} F$). Los condensadores se pueden producir en varias formas y tamaños ().

Podemos calcular la capacitancia de un par de conductores con el enfoque estándar que sigue.
Estrategia de resolución de problemas: cálculo de la capacitancia
1. Supón que el condensador tiene una carga $Q$.
2. Determina el campo eléctrico $\overrightarrow{\bold{E}}$ entre los conductores. Si la simetría está presente en la disposición de los conductores, es posible que puedas usar la ley de Gauss para este cálculo.
3. Encuentra la diferencia de potencial entre los conductores de
$$V_B - V_A = -\int_A^B \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}} \tag{8.2}$$donde el camino de integración conduce de un conductor a otro. La magnitud de la diferencia de potencial es entonces $V = |V_B - V_A|$
4. Conociendo $V$, obtén la capacitancia directamente de la Ecuación 8.1.
Para mostrar cómo funciona este procedimiento, ahora calculamos las capacitancias de capacitores cilíndricos, esféricos y de placa paralela. En todos los casos, suponemos condensadores de vacío (condensadores vacíos) sin sustancia dieléctrica en el espacio entre conductores.
El condensador de placas paralelas () tiene dos placas conductoras idénticas, cada una con un área superficial $A$, separadas por una distancia $d$. Cuando se aplica una tensión $V$ al condensador, almacena una carga $Q$, como se muestra. Podemos ver cómo su capacitancia puede depender de $A$ y $D$ al considerar las características de la fuerza de Coulomb. Sabemos que la fuerza entre las cargas aumenta con los valores de carga y disminuye con la distancia entre ellas. Deberíamos esperar que cuanto más grandes sean las placas, más carga podrán almacenar. Por lo tanto, $C$ debería ser mayor para un valor mayor de $A$. De manera similar, cuanto más juntas estén las placas, mayor será la atracción de las cargas opuestas sobre ellas. Por lo tanto, $C$ debería ser mayor para una d más pequeña.
Definimos la densidad de carga superficial $σ$ en las placas como
$$σ = \frac{Q}{A}$$Sabemos por capítulos anteriores que cuando d es pequeño, el campo eléctrico entre las placas es bastante uniforme (ignorando los efectos de borde) y que su magnitud viene dada por
$$E = \frac{σ}{ε_0}$$donde la constante $ε_0$ es la permitividad del espacio libre, $ε_0 = 8.85 × 10^{-12} F/m$. La unidad del SI de $F/m$ es equivalente a $C^2/ N \cdot m^2$. Como el campo eléctrico $\overrightarrow{\bold{E}}$ entre las placas es uniforme, la diferencia de potencial entre las placas es
$$V = Ed = \frac{σd}{ε_0} = \frac{Qd}{ε_0A}$$Por lo tanto, la ecuación 8.1 da la capacidad de un condensador de placa paralela como
Nótese en esta ecuación que la capacitancia es una función solamente de la geometría y qué material llena el espacio entre las placas (en este caso, el vacío) de este condensador. De hecho, esto es cierto no solo para un condensador de placas paralelas, sino para todos los condensadores: la capacitancia es independiente de $Q$ o $V$. Si la carga cambia, el potencial cambia correspondientemente para que $Q/V$ permanezca constante.
Ejemplo 8.1
Capacitancia y carga almacenadas en un condensador de placa paralela
(a) ¿Cuál es la capacidad de un condensador de placas paralelas vacío con placas de metal que tienen un área de $1.00 m^2$, separadas por $1.00 mm$? (b) ¿Cuánta carga se almacena en este condensador si se le aplica un voltaje de $3.00 × 10^3 V$?
Estrategia
Encontrar la capacitancia $C$ es una aplicación directa de la ecuación 8.3. Una vez que encontramos $C$, podemos encontrar la carga almacenada usando la Ecuación 8.1.
Solución
a. Ingresando los valores dados en la Ecuación 8.3
Este pequeño valor de capacitancia indica qué tan difícil es hacer un dispositivo con una gran capacidad.
b. Al invertir la ecuación 8.1 e ingresar los valores conocidos en esta ecuación, obtenemos
$$Q = CV = (8.85 × 10^{−9} F)(3.00 × 10^3 V) = 26.6 μC$$Explicación
Esta carga es solo un poco mayor que las que se encuentran en aplicaciones típicas de electricidad estática. Como el aire se descompone (se vuelve conductor) con una intensidad de campo eléctrico de aproximadamente $3,0 MV/m$, no se puede almacenar más carga en este condensador aumentando el voltaje.
Ejemplo 8.2
Un condensador $1-F$ de placa paralela
Supón que deseas construir un condensador de placa paralela con una capacidad de $1.0 F$. ¿Qué área debes usar para cada placa si las placas están separadas por $1.0 mm$?
Solución
Reordenando la ecuación 8.3, obtenemos
$$A = \frac{Cd}{ε_0} = \frac{(1.0F)(1.0 × 10^{-3} m)}{8.85 × 10^{-12} F/m} = 1.1 × 10^8 m^2$$Este pequeño valor de capacitancia indica qué tan difícil es
Cada placa cuadrada debería tener $10 km$ de ancho. Solía ser una broma común pedirle a un alumno que vaya al almacén del laboratorio y solicite un condensador de placa paralela de $1 F$, hasta que los encargados del almacén se cansaran de la broma.
 Comprueba tu aprendizaje 8.1
Comprueba tu aprendizaje 8.1
 Comprueba tu aprendizaje 8.2
Comprueba tu aprendizaje 8.2
Un condensador esférico es otro conjunto de conductores cuya capacitancia se puede determinar fácilmente (). Consiste en dos conchas esféricas conductoras concéntricas de radios $R_1$ (caparazón interior) y $R_2$ (carcasa externa). Las conchas reciben cargas iguales y opuestas $+Q$ y $-Q$, respectivamente.
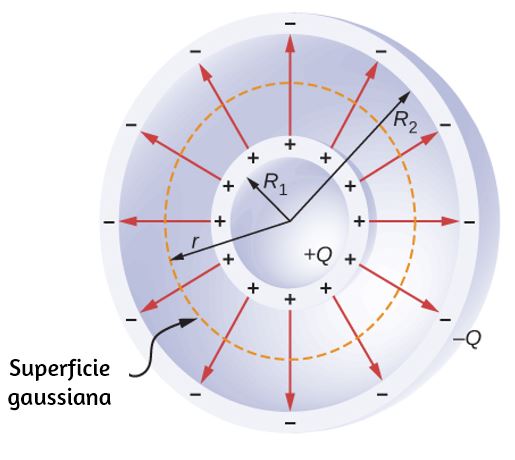
Desde la simetría, el campo eléctrico entre las conchas se dirige radialmente hacia afuera. Podemos obtener la magnitud del campo aplicando la ley de Gauss sobre una superficie gaussiana esférica de radio r concéntrico con las conchas. La carga incluida es $+Q$; por lo tanto, tenemos
$$\oint_S\overrightarrow{\bold{E}} \cdot \^{n}da = E4πr^2 = \frac{Q}{ε_0}$$Por lo tanto, el campo eléctrico entre los conductores es
$$\overrightarrow{\bold{E}} = \frac{1}{4πε_0}\frac{Q}{r^2}\^{r}$$Sustituimos este $\overrightarrow{\bold{E}}$ en la Ecuación 8.2 e integramos a lo largo de una trayectoria radial entre las capas:
$$\begin{split} \int_{R_1}^{R_2} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}} &= \int_{R_1}^{R_2} \left(\frac{1}{4πε_0} \frac{Q}{r^2}\^{r} \right) \cdot (\^{r}dr) \\ &= \frac{Q}{4πε_0} \int_{R_1}^{R_2} \frac{dr}{r^2} = \frac{Q}{4πε_0} \left(\frac{1}{R_1} - \frac{1}{R_2} \right) \end{split}$$En esta ecuación, la diferencia de potencial entre las placas es $V = -(V_2 - V_1) = V_1 - V_2$. Sustituimos este resultado en la Ecuación 8.1 para hallar la capacitancia de un condensador esférico:
Ejemplo 8.3
Capacitancia de una esfera aislada
Calcula la capacitancia de una sola esfera conductora aislada de radio $R_1$ y compárala con la ecuación 8.4 en el límite con $R_2 → ∞$.
Estrategia
Suponemos que la carga en la esfera es $Q$, por lo que seguimos los cuatro pasos descritos anteriormente. También asumimos que el otro conductor es una esfera concéntrica hueca de radio infinito.
Solución
En el exterior de una esfera conductora aislada, el campo eléctrico está dado por la Ecuación 8.2. La magnitud de la diferencia de potencial entre la superficie de una esfera aislada y el infinito es
$$\begin{split} \int_{R_1}^{+∞} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}} &= \left(\frac{Q}{4πε_0} \int_{R_1}^{+∞} \frac{1}{r^2}\^{r}\right) \cdot (\^{r}dr) \\ &= \frac{Q}{4πε_0} \int_{R_1}^{+∞} \frac{dr}{r^2} = \frac{Q}{4πε_0}\frac{Q}{R_1} \end{split}$$La capacitancia de una esfera aislada es por lo tanto
$$C = \frac{Q}{V} = Q\frac{4πε_0R_1}{Q} = 4πε_0R_1$$Explicación
Se puede obtener el mismo resultado tomando el límite de la Ecuación 8.4 como $R_2 → ∞$. Una sola esfera aislada es, por lo tanto, equivalente a un condensador esférico cuya carcasa exterior tiene un radio infinitamente grande.
 Comprueba tu aprendizaje 8.3
Comprueba tu aprendizaje 8.3
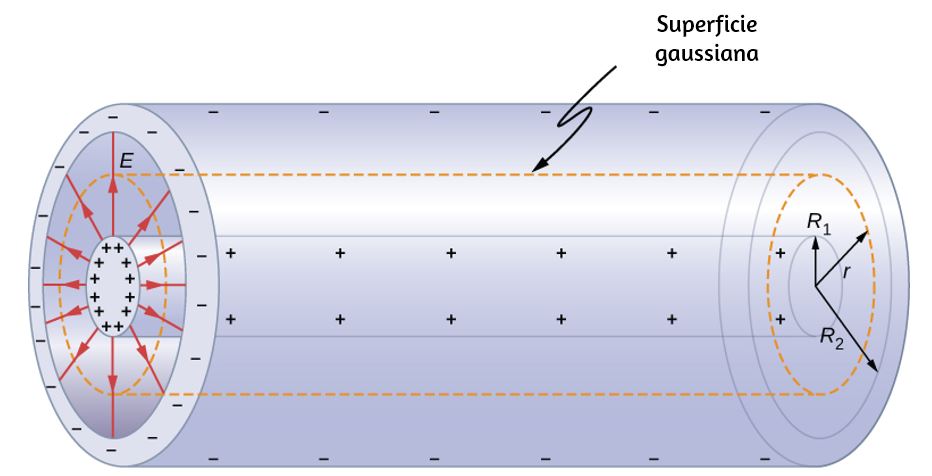
Un condensador cilíndrico consta de dos cilindros concéntricos y conductores (). El cilindro interior, de radio $R_1$, puede ser un caparazón o ser completamente sólido. El cilindro exterior es un caparazón de radio interior $R_2$. Suponemos que la longitud de cada cilindro es $l$ y que el exceso de cargas $+Q$ y $-Q$ reside en los cilindros interior y exterior, respectivamente.
Con los efectos de borde ignorados, el campo eléctrico entre los conductores se dirige radialmente hacia afuera desde el eje común de los cilindros. Usando la superficie gaussiana que se muestra en la , tenemos
$$\oint_S\overrightarrow{\bold{E}} \cdot \^{n}dA = E(2πrl) = \frac{Q}{ε_0}$$Por lo tanto, el campo eléctrico entre los cilindros es
$$\overrightarrow{\bold{E}} = \frac{1}{2πε_0}\frac{Q}{rl}\^{r} \tag{8.5}$$Aquí $\^{r}$ es el vector radial unitario a lo largo del radio del cilindro. Podemos sustituir en la Ecuación 8.2 y encontrar la diferencia de potencial entre los cilindros:
$$\begin{split} V &= \int_{R_1}^{R_2} \overrightarrow{\bold{E}} \cdot d\overrightarrow{\bold{l}}^p = \frac{Q}{2πε_0l} \int_{R_1}^{R_2} \frac{1}{r}\^{r} \cdot (\^{r}dr) \\ &= \frac{Q}{2πε_0l} \int_{R_1}^{R_2} \frac{dr}{r} = \frac{Q}{2πε_0l}ln\frac{R_2}{R_1} \end{split}$$Por lo tanto, la capacidad de un condensador cilíndrico es
Como en otros casos, esta capacitancia depende solo de la geometría de la disposición del conductor. Una aplicación importante de la Ecuación 8.6 es la determinación de la capacidad por unidad de longitud de un cable coaxial, que se usa comúnmente para transmitir señales eléctricas variables en el tiempo. Un cable coaxial consiste en dos conductores cilíndricos concéntricos separados por un material aislante (aquí, suponemos que hay un vacío entre los conductores, pero la física es casi idéntica cuando el espacio entre los conductores se llena con un dieléctrico). Esta configuración protege la señal eléctrica que se propaga por el conductor interno de campos eléctricos extraviados externos al cable. La corriente fluye en direcciones opuestas en los conductores interno y externo, con el conductor externo generalmente conectado a tierra.
Ahora, a partir de la Ecuación 8.6, la capacitancia por unidad de longitud del cable coaxial está dada por
$$\frac{C}{l} = \frac{2πε_0}{ln(R_2/R_1)}$$En aplicaciones prácticas, es importante seleccionar valores específicos de $C/l$. Esto se puede lograr con elecciones adecuadas de radios de los conductores y del material aislante entre ellos.
 Comprueba tu aprendizaje 8.4
Comprueba tu aprendizaje 8.4
Varios tipos de condensadores prácticos se muestran en la . Los condensadores comunes a menudo están hechos de dos pequeñas piezas de lámina de metal separadas por dos pequeños pedazos de aislamiento (observa la (b)). La lámina de metal y el aislante están envueltos en una capa protectora, y dos cables de metal se utilizan para conectar las láminas a un circuito externo. Algunos materiales aislantes comunes son mica, cerámica, papel y recubrimiento antiadherente Teflon™.
Otro tipo popular de condensador es un condensador electrolítico. Consiste en un metal oxidado en una pasta conductora. La principal ventaja de un condensador electrolítico es su alta capacitancia en relación con otros tipos comunes de condensadores. Por ejemplo, la capacitancia de un tipo de condensador electrolítico de aluminio puede ser tan alta como $1.0 F$.
Sin embargo, debes tener cuidado al usar un condensador electrolítico en un circuito, ya que solo funciona correctamente cuando la lámina metálica tiene un potencial mayor que la pasta conductora. Cuando ocurre la polarización inversa, la acción electrolítica destruye la película de óxido. Este tipo de condensador no se puede conectar a través de una fuente de corriente alterna, porque la mitad del tiempo, el voltaje de CA tendría la polaridad incorrecta, ya que una corriente alterna revierte su polaridad.
Un condensador de aire variable () tiene dos juegos de placas paralelas. Un juego de placas está fijo (indicado como "estator"), y el otro conjunto de placas está unido a un eje que se puede girar (indicado como "rotor").

Al girar el eje, se puede cambiar el área de la sección transversal en la superposición de las placas; por lo tanto, la capacitancia de este sistema puede ajustarse a un valor deseado. La sintonización de condensadores tiene aplicaciones en cualquier tipo de transmisión de radio y en la recepción de señales de radio. Cada vez que ajustes la radio de tu automóvil a tu estación favorita, piensa en la capacitancia.
Los símbolos que se muestran en la son representaciones de circuitos de varios tipos de condensadores. Generalmente usamos el símbolo que se muestra en la (a). El símbolo en la (c) representa un condensador de capacitancia variable. Observa la similitud de estos símbolos con la simetría de un condensador de placa paralela. Un condensador electrolítico está representado,en parte, por el símbolo de la (b), donde la placa curva indica el terminal negativo.
Un interesante ejemplo aplicado de un modelo de condensador proviene de la biología celular y se trata del potencial eléctrico en la membrana plasmática de una célula viva (). Las membranas celulares separan las células de su entorno pero permiten que algunos iones seleccionados entren o salgan de la célula. La diferencia de potencial a través de una membrana es de aproximadamente $70 mV$. La membrana celular puede tener un grosor de $7$ a $10 nm$. Al tratar la membrana celular como un condensador de tamaño nanométrico, la estimación de la intensidad de campo eléctrico más pequeña en sus "placas" produce el valor $E = \frac{V}{d} = \frac{70 × 10^{-3} V}{10 × 10^{-9} m} = 7 × 10^6 V/m > 3 MV/m$.
Esta magnitud del campo eléctrico es lo suficientemente grande como para crear una chispa eléctrica en el aire.
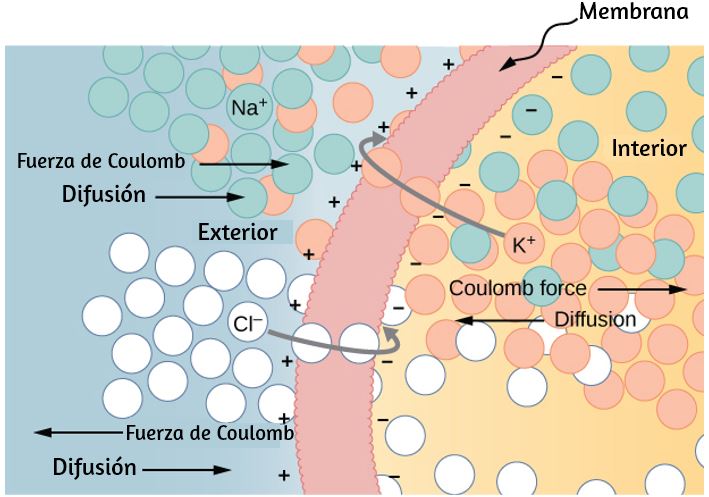
En el siguiente objeto interactivo de PhET Simulaciones, explora como funciona un Condensador. Cambia el tamaño de las placas y la distancia entre ellas. Cambia el voltaje y observa las cargas acumuladas en las placas. Conecta un condensador cargado a un foco y observa como se descarga el circuito.
Observa el campo eléctrico y mide el voltaje. Predice cómo cambia la capacitancia cuando el área de las placas o la separación entre placas cambia.
Varios condensadores se pueden conectar entre sí para ser utilizados en una variedad de aplicaciones. Las conexiones múltiples de condensadores se comportan como un solo condensador equivalente. La capacidad total de este condensador único equivalente depende tanto de los condensadores individuales y de cómo están conectados. Los condensadores se pueden organizar en dos tipos de conexiones simples y comunes, conocidas como series y paralelas, para las cuales podemos calcular fácilmente la capacidad total. Estas dos combinaciones básicas, serie y paralelo, también se pueden usar como parte de conexiones más complejas.
La ilustra una combinación en serie de tres condensadores, dispuestos en una fila dentro del circuito. Como para cualquier condensador, la capacitancia de la combinación se relaciona con la carga y el voltaje usando la Ecuación 8.1. Cuando esta combinación en serie se conecta a una batería con voltaje $V$, cada uno de los condensadores adquiere una carga idéntica $Q$. Para explicar, primero ten en cuenta que la carga en la placa conectada al terminal positivo de la batería es $+Q$ y la carga en la placa conectada al terminal negativo es $-Q$. Luego se inducen cargas en las otras placas de modo que la suma de las cargas en todas las placas y la suma de las cargas en cualquier par de placas del capacitor sea cero. Sin embargo, la caída de potencial $V_1 = Q/C_1$ en un condensador puede ser diferente de la caída potencial $V_2 = Q/C_2$ en otro condensador, porque, en general, los condensadores pueden tener capacidades diferentes. La combinación en serie de dos o tres condensadores se asemeja a un solo condensador con una capacidad más pequeña.
Generalmente, cualquier cantidad de condensadores conectados en serie es equivalente a un condensador cuya capacitancia (llamada capacitancia equivalente) es más pequeña que la más pequeña de las capacitancias en la combinación en serie. La carga en este condensador equivalente es la misma que la carga en cualquier condensador en una combinación en serie: Es decir, todos los condensadores de una combinación en serie tienen la misma carga. Esto ocurre debido a la conservación de carga en el circuito. Cuando una carga $Q$ en un circuito en serie se elimina de una placa del primer condensador (que denotamos como $-Q$), debe colocarse en una placa del segundo condensador (que denotamos como $+Q$), y así sucesivamente.
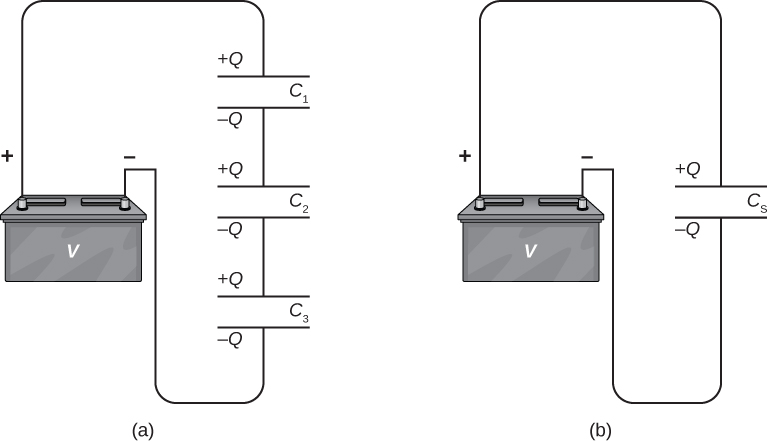
Podemos encontrar una expresión para la capacitancia total (equivalente) considerando los voltajes a través de los condensadores individuales. Los potenciales a través de los condensadores $1$, $2$ y $3$ son, respectivamente, $V_1 = Q/C_1$, $V_2 = Q/C_2$ y $V_3 = Q/C_3$. Estos potenciales deben sumar el voltaje de la batería, dando el siguiente equilibrio potencial: $$V = V_1 + V_2 + V_3$$
El potencial $V$ se mide a través de un condensador equivalente que mantiene la carga $Q$ y tiene una capacitancia equivalente $C_S$. Ingresando las expresiones para $V_1$, $V_2$ y $V_3$, obtenemos
$$\frac{Q}{C_S} = \frac{Q}{C_1} + \frac{Q}{C_2} + \frac{Q}{C_3}$$Al cancelar la carga $Q$, obtenemos una expresión que contiene la capacitancia equivalente, $C_S$, de tres condensadores conectados en serie: $$\frac{1}{C_S} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$$
Esta expresión se puede generalizar a cualquier cantidad de condensadores en una red en serie.
Combinaciones en serie
Para condensadores conectados en una combinación en serie, el recíproco de la capacitancia equivalente es la suma de los recíprocos de capacitancias individuales:
$$\frac{1}{C_S} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} ... \tag{8.7}$$Ejemplo 8.4
Capacitancia equivalente de un circuito en serie
Encuentra la capacidad total para tres condensadores conectados en serie, dado que sus capacitancias individuales son $1.000 μF$, $5.000 μF$ y $8,000 μF$.
Estrategia
Como solo hay tres condensadores en esta red, podemos encontrar la capacitancia equivalente usando la Ecuación 8.7 con tres términos.
Solución
Ingresamos las capacitancias dadas en la Ecuación 8.7:
$$\begin{split} \frac{1}{C_S} &= \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} \\ &= \frac{1}{1.000 μF} + \frac{1}{5.000 μF} + \frac{1}{8.000 μF} \end{split}$$ $$\frac{1}{C_S} = \frac{1.325}{μF}$$Ahora invertimos este resultado y obtenemos $C_S = \dfrac{μF}{1.325} = 0.755 μF$
Explicación
Ten en cuenta que en una red de condensadores en serie, la capacitancia equivalente es siempre menor que la capacitancia individual más pequeña en la red.
En la (a) se ilustra una combinación en paralelo de tres condensadores, con una placa de cada condensador conectada a un lado del circuito y la otra placa conectada al otro lado. Como los condensadores están conectados en paralelo, todos tienen el mismo voltaje $V$ en sus placas. Sin embargo, cada condensador en la red paralela puede almacenar una carga diferente.
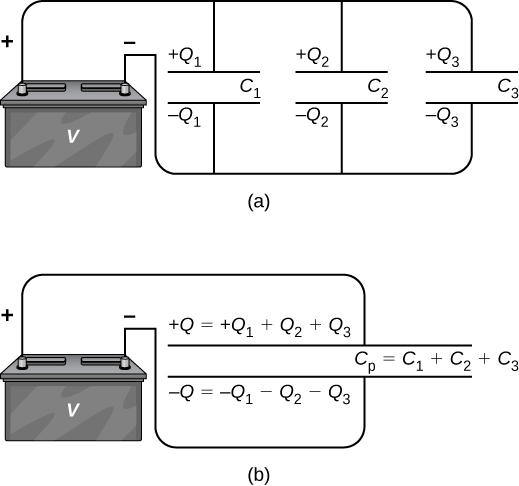
Para encontrar la capacitancia equivalente $C_P$ de la red paralela, observamos que la carga total $Q$ almacenada por la red es la suma de todas las cargas individuales:
$$Q = Q_1 + Q_2 + Q_3.$$En el lado izquierdo de esta ecuación, usamos la relación $Q = C_PV$, que se aplica a toda la red. En el lado derecho de la ecuación, usamos las relaciones $Q_1 = C_1V$, $Q_2 = C_2V$ y $Q_3 = C_3V$ para los tres condensadores en la red. De esta forma obtenemos
$$C_PV = C_1V + C_2V + C_3V$$Esta ecuación, cuando se simplifica, es la expresión de la capacitancia equivalente de la red paralela de tres condensadores:
$$C_P = C_1 + C_2 + C_3.$$Esta expresión se generaliza fácilmente a cualquier cantidad de condensadores conectados en paralelo en la red.
Combinación en paralelo
Para capacitores conectados en una combinación en paralelo, la capacitancia equivalente (neta) es la suma de todas las capacitancias individuales en la red,
$$C_PV = C_1V + C_2V + C_3V + ... \tag{8.8}$$Ejemplo 8.5
Capacitancia equivalente de un circuito en paralelo
Encuentra la capacitancia neta para tres condensadores conectados en paralelo, dado que sus capacitancias individuales son $1.0 μF$, $5.0 μF$ y $8.0μF$.
Estrategia
Como solo hay tres condensadores en esta red, podemos encontrar la capacitancia equivalente usando la Ecuación 8.8 con tres términos.
Solución
Ingresando las capacidades dadas en la Ecuación 8.8, obtenemos:
$$C_P = C_1 + C_2 + C_3 = 1.0 μF + 5.0 μF + 8.0 μF = 14.0 μF$$Explicación
Tenga en cuenta que en una red de condensadores en paralelo, la capacidad equivalente es siempre mayor que cualquiera de las capacitancias individuales en la red.
Las redes de condensadores suelen ser una combinación de conexiones en serie y paralelas, como se muestra en la . Para encontrar la capacitancia neta de tales combinaciones, identificamos las partes que contienen solo series o solo conexiones paralelas, y encontramos sus capacidades equivalentes. Repetimos este proceso hasta que podamos determinar la capacitancia equivalente de toda la red. El siguiente ejemplo ilustra este proceso.
Ejemplo 8.6
Capacitancia equivalente de una red
Encuentra la capacitancia total de la combinación de condensadores que se muestra en la . Supongamos que las capacidades se conocen por tres decimales ($C_1 = 1.000 μF$, $C_2 = 5.000 μF$, $C_3 = 8,000 μF$). Redondea tu respuesta a tres cifras decimales.
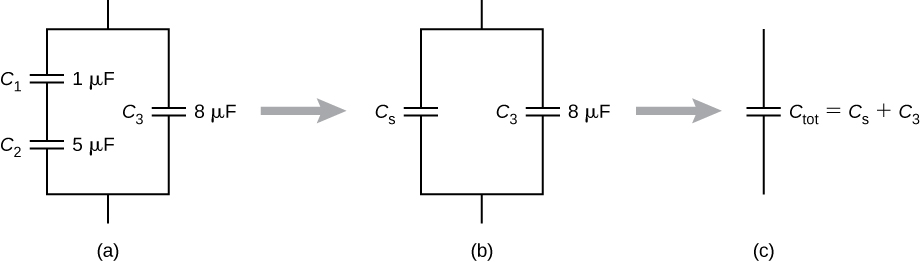
Estrategia
Primero identificamos qué condensadores están en serie y cuáles están en paralelo. Los condensadores $C_1$ y $C_2$ están en serie. Su combinación, etiquetada $C_S$, está en paralelo con $C_3$.
Solución
Como $C_1$ y $C_2$ están en serie, su capacitancia equivalente $C_S$ se obtiene con la Ecuación 8.7:
$$\frac{1}{C_S} = \frac{1}{C_1} + \frac{1}{C_2} = \frac{1}{1.000 μF}+ \frac{1}{5.000 μF} = \frac{1.200}{μF}$$Invirtiendo:
$$C_S = 0.833 μF$$La capacitancia $C_S$ se conecta en paralelo con la tercera capacitancia $C_3$, por lo que usamos la ecuación 8.8 para encontrar la capacitancia C equivalente de toda la red:
$$C = C_S + C_3 = 0,833 μF + 8,000 μF = 8,833 μF.$$En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, puedes obtener varias configuraciones de red. Calcula la capacitancia equivalente de toda la red, para cada ejercicio que selecciones.
Halla la capacitancia equivalente
Ejemplo 8.7
Red de Condensadores
Determina la capacitancia neta $C$ de la combinación de capacitores que se muestra en la cuando las capacitancias son $C_1 = 12.0 μF$, $C_2 = 2.0 μF$ y $C_3 = 4.0μF$. Cuando se mantiene una diferencia de potencial de $12.0 V$ a través de la combinación, encuentra la carga y el voltaje en cada condensador.
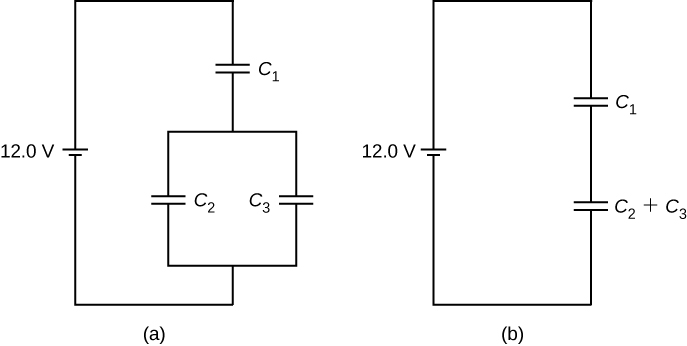
Estrategia
Primero calculamos la capacitancia neta $C_{23}$ de la conexión paralela $C_2$ y $C_3$. Entonces $C$ es la capacitancia neta de la conexión en serie $C_1$ y $C_{23}$. Usamos la relación $C = Q/V$ para encontrar las cargas $Q_1$, $Q_2$ y $Q_3$, y los voltajes $V_1$, $V_2$ y $V_3$, a través de los condensadores $1$, $2$ y $3$, respectivamente.
Solución
La capacitancia equivalente para $C_2$ y $C_3$ es
La combinación completa de tres condensadores es equivalente a dos condensadores en serie,
$$\frac{1}{C} = \frac{1}{12.0 μF} + \frac{1}{6.0 μF} + \frac{1}{4.0 μF} → C = 4.0 μF$$Considera la combinación equivalente de dos condensadores en la (b). Como los condensadores están en serie, tienen la misma carga, $Q_1 = Q_{23}$. Además, los condensadores comparten la diferencia de potencial $12.0 V$, por lo que
$$\begin{split} 12.0 V &= V_1 + V_{23} = \frac{Q_1}{C_1} + \frac{Q_{23}}{C_{23}} = \frac{Q_1}{12.0 μF} + \frac{Q_1}{6.0 μF} → Q_1 \\ &= 48.0 μC \end{split}$$Ahora la diferencia de potencial a través del condensador 1 es
$$V_1 = \frac{Q_1}{C_1} = \frac{48.0 μC}{12.0 μF} = 4.0 V$$Debido a que los condensadores $2$ y $3$ están conectados en paralelo, tienen el mismo diferencial de potencial:
$$V_2= V_3 = 12.0 V - 4.0 V = 8.0 V.$$Por lo tanto, las cargas en estos dos condensadores son, respectivamente,
$$\begin{split} Q_2 &= C_2V_2 = (2.0 μF)(8.0 V) = 16.0 μC, Q_3 = C_3V_3 \\ &= (4.0 μF)(8.0 V) = 32.0 μC \end{split}$$Explicación
Como se esperaba, la carga neta en la combinación paralela de $C_2$ y $C_3$ es $Q_{23} = Q_2+ Q_3 = 48.0 μC$.
 Comprueba tu aprendizaje 8.5
Comprueba tu aprendizaje 8.5
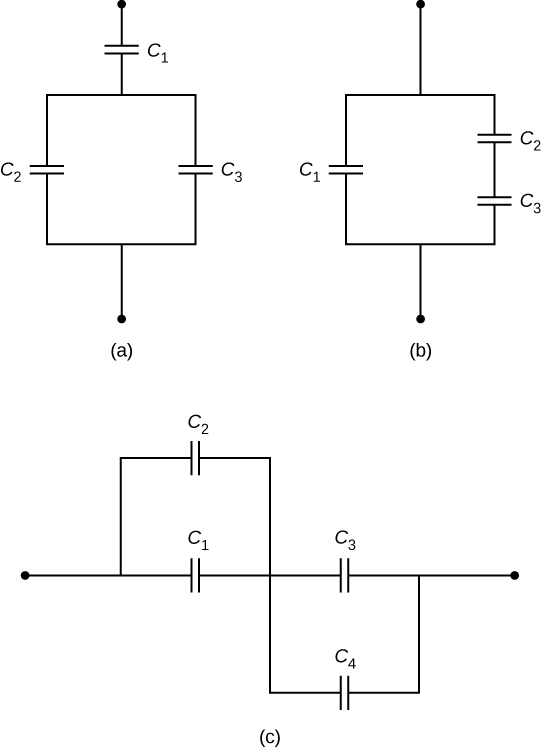
La mayoría de nosotros hemos visto dramatizaciones de personal médico que usa un desfibrilador para pasar una corriente eléctrica a través del corazón de un paciente para hacer que su latido sea normal. A menudo es realista en el detalle, la persona que aplica el choque indica a otra persona "haz $400$ julios esta vez". La energía suministrada por el desfibrilador se almacena en un condensador y puede ajustarse para adaptarse a la situación. A menudo se emplean unidades del SI en joules. Menos dramático es el uso de condensadores en microelectrónica para suministrar energía cuando las baterías están cargadas (). Los condensadores también se utilizan para suministrar energía al flash de las lámparas de las cámaras.

La energía almacenada en un condensador ($U_C$) es energía potencial electrostática y, por lo tanto, está relacionada con la carga $Q$ y el voltaje $V$ entre las placas del condensador. Un condensador cargado almacena energía en el campo eléctrico entre sus placas. A medida que el capacitor se está cargando, el campo eléctrico se acumula. Cuando un condensador cargado se desconecta de una batería, su energía permanece en el campo, en el espacio entre sus placas.
Para obtener información sobre cómo se puede expresar esta energía (en términos de $Q$ y $V$), considera un condensador de placa paralela cargado y vacío; es decir, un condensador sin dieléctrico pero con un vacío entre sus placas. El espacio entre sus placas tiene un volumen $Ad$, y se llena con un campo electrostático uniforme $E$. La energía total $U_C$ del condensador está contenida dentro de este espacio. La densidad de energía $u_E$ en este espacio es simplemente $U_C$ dividida por el volumen $Ad$. Si conocemos la densidad de energía, la energía se puede encontrar como $U_C = u_E(Ad)$. La densidad de energía $u_E$ en una región de espacio libre ocupada por un campo eléctrico $E$ depende solo de la magnitud del campo y es
Si multiplicamos la densidad de energía por el volumen entre las placas, obtenemos la cantidad de energía almacenada entre las placas de un condensador de placas paralelas: $U_C = u_C(Ad) = \frac{1}{2}ε_0E^2Ad = \frac{1}{2}ε_0\frac{V^2}{d^2}Ad = \frac{1}{2}V^2ε_0Ad = \frac{1}{2}V^2C$.
En esta derivación, utilizamos el hecho de que el campo eléctrico entre las placas es uniforme de modo que $E = V/d$ y $C = ε_0A/d$. Debido a que $C = Q/V$, podemos expresar este resultado en otras formas equivalentes:
La expresión en la Ecuación 8.10 para la energía almacenada en un condensador de placa paralela es generalmente válida para todos los tipos de condensadores. Para ver esto, considera cualquier condensador descargado (no necesariamente un tipo de placa paralela). En algún momento, lo conectamos a través de una batería, dándole una diferencia de potencial $V = q/C$ entre sus placas. Inicialmente, la carga en las placas es $Q = 0$. A medida que el condensador se está cargando, la carga se acumula gradualmente en sus placas, y después de un tiempo, alcanza el valor $Q$. Para mover una carga infinitesimal $dq$ desde la placa negativa a la placa positiva (de un potencial inferior a uno superior), la cantidad de trabajo $dW$ que se debe hacer en dq es $dW = Vdq = \frac{q}{C}dq$.
Este trabajo se convierte en la energía almacenada en el campo eléctrico del condensador. Para cargar el condensador a una carga $Q$, el trabajo total requerido es
$$W = \int_0^{W(Q)} dW = \int_0^Q \frac{q}{C}dq = \frac{1}{2}\frac{Q^2}{C}$$Como la geometría del condensador no se ha especificado, esta ecuación se cumple para cualquier tipo de condensador. El trabajo total $W$ que se necesita para cargar un condensador es la energía potencial eléctrica $U_C$ almacenada en él, o $U_C = W$. Cuando la carga se expresa en coulombs, el potencial se expresa en voltios, y la capacitancia se expresa en faradios, esta relación da la energía en julios.
Sabiendo que la energía almacenada en un condensador es $U_C = Q^2/(2C)$, ahora podemos encontrar la densidad de energía $u_E$ almacenada en un vacío entre las placas de un condensador de placa paralela cargado.
Solo tenemos que dividir $U_C$ por el volumen $Ad$ del espacio entre sus placas y tener en cuenta que para un condensador de placas paralelas, tenemos $E = σ/ε_0$ y $C = ε_0A/d$. Por lo tanto, obtenemos
$$\begin{split} u_E &= \frac{u_C}{Ad} = \frac{1}{2}\frac{Q^2}{C}\frac{1}{Ad} \\ &= \frac{1}{2}\frac{Q^2}{ε_0A/d}\frac{1}{Ad} = \frac{1}{2}\frac{1}{ε_0}(Q/A)^2 = \frac{σ^2}{2ε_0} \\ &= \frac{(Eε_0)^2}{2ε_0} = \frac{ε_0}{2}E^2 \end{split}$$Vemos que esta expresión para la densidad de energía almacenada en un condensador de placa paralela está de acuerdo con la relación general expresada en la ecuación 8.9. Podríamos repetir este cálculo para un condensador esférico o un condensador cilíndrico u otros condensadores, y en todos los casos, terminaríamos con la relación general dada por la ecuación 8.9.
Ejemplo 8.8
Energía almacenada en un condensador
Calcula la energía almacenada en la red del condensador en la figura (a) cuando los condensadores están completamente cargados y cuando las capacidades son $C_1 = 12.0 μF$, $C_2 = 2.0 μF$ y $C_3 = 4.0 μF$, respectivamente.
Estrategia
Usamos la Ecuación 8.10 para encontrar la energía $U_1$, $U_2$ y $U_3$ almacenadas en los condensadores $1$, $2$ y $3$, respectivamente. La energía total es la suma de todas estas energías.
Solución
Identificamos $C_1 = 12.0 μF$ y $V_1 = 4.0 V$, $C_2 = 2.0 μF$ y $V_2 = 8.0 V$, $C_3 = 4.0 μF$ y $V_3 = 8.0 V$. Las energías almacenadas en estos condensadores son
$$U_1 = \frac{1}{2}C_1V_1^2 = \frac{1}{2}(12.0 μF)(4.0 V)^2 = 96 μJ$$ $$U_2 = \frac{1}{2}C_2V_2^2 = \frac{1}{2}(2.0 μF)(8.0 V)^2 = 64 μJ$$ $$U_3 = \frac{1}{2}C_3V_3^2 = \frac{1}{2}(4.0 μF)(8.0 V)^2 = 130 μJ$$La energía total almacenada en esta red es
$$U_C = U_1 + U_2 + U_3 = 96 μJ + 64 μJ + 130 μJ = 0.29 mJ$$Explicación
Podemos verificar este resultado calculando la energía almacenada en el condensador simple de $4.0 μF$, que se considera equivalente a toda la red. El voltaje a través de la red es $12.0 V$. La energía total obtenida de esta manera concuerda con nuestro resultado obtenido previamente, $U_C = \frac{1}{2}CV^2 = \frac{1}{2}(4.0 μF) (12.0 V)^2 = 0.29 mJ$.
 Comprueba tu aprendizaje 8.6
Comprueba tu aprendizaje 8.6
En una emergencia cardíaca, un dispositivo electrónico portátil conocido como desfibrilador externo automático (AED) puede salvarte la vida. Un desfibrilador () administra una carga grande en una ráfaga corta, o un choque, al corazón de una persona para corregir el ritmo cardíaco anormal (una arritmia). Un ataque al corazón puede surgir desde el inicio de latidos rápidos e irregulares del corazón, llamado fibrilación cardíaca o ventricular. La aplicación de una gran descarga de energía eléctrica puede terminar con la arritmia y permitir que el marcapasos natural del cuerpo reanude su ritmo normal. Hoy en día, es común que las ambulancias lleven AED. Los AED también se encuentran en muchos lugares públicos. Estos están diseñados para ser utilizados por personas legas. El dispositivo automáticamente diagnostica el ritmo cardíaco del paciente y luego aplica la descarga con la energía y la forma de onda apropiadas.
En muchos casos se recomienda la RCP (reanimación cardiopulmonar) antes de usar un desfibrilador.
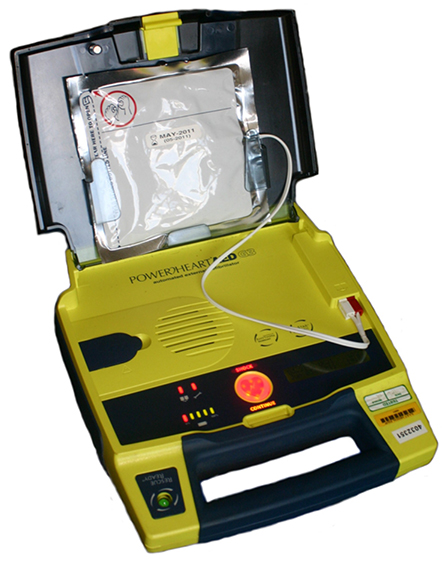
Ejemplo 8.9
Capacitancia de un desfibrilador cardíaco
Un desfibrilador cardíaco entrega $4.00 × 10^2 J$ de energía descargando un condensador inicialmente a $1.00 × 10^4 V$. ¿Cuál es su capacitancia?
Estrategia
Nos dan $U_C$ y $V$, y se nos pide que encontremos la capacitancia $C$. Resolvemos la Ecuación 8.10 para $C$ y la sustituimos.
Solución
Al resolver esta expresión para $C$ e ingresar los valores dados, obtenemos $C = 2\dfrac{U_C}{V^2} = 2\dfrac{4.00 × 10^2 J}{(1.00 × 10^4 V)^2} = 8.00 μF$
Como discutimos anteriormente, un material aislante colocado entre las placas de un condensador se llama dieléctrico. Insertar un dieléctrico entre las placas de un condensador afecta su capacitancia. Para ver por qué, consideremos un experimento descrito en la .
Inicialmente, un condensador con capacitancia $C_0$ cuando hay aire entre sus placas es cargado por una batería al voltaje $V_0$. Cuando el condensador está completamente cargado, la batería está desconectada. Luego, una carga $Q_0$ reside en las placas, y la diferencia de potencial entre las placas se mide como $V_0$. Ahora, supongamos que insertamos un dieléctrico que llena totalmente el espacio entre las placas.
Si monitoreamos el voltaje, encontramos que la lectura del voltímetro ha caído a un valor menor $V$. Escribimos este nuevo valor de voltaje como una fracción del voltaje original $V_0$, con un número positivo $κ$, $κ > 1$:
$$V = \frac{1}{κ}V_0$$La constante $κ$ en esta ecuación se llama constante dieléctrica del material entre las placas, y su valor es característico para el material. Una explicación detallada de por qué el dieléctrico reduce el voltaje se da en la siguiente sección. Los diferentes materiales tienen diferentes constantes dieléctricas (en la siguiente sección se proporciona una tabla de valores para materiales típicos). Una vez que la batería se desconecta, no hay una ruta para que fluya una carga a la batería desde las placas del capacitor. Por lo tanto, la inserción del dieléctrico no tiene ningún efecto sobre la carga en la placa, que permanece en un valor de $Q_0$. Por lo tanto, encontramos que la capacitancia del condensador con un dieléctrico es
Esta ecuación nos dice que la capacitancia $C_0$ de un condensador vacío se puede incrementar por un factor $κ$ cuando insertamos un material dieléctrico para llenar completamente el espacio entre sus placas. Ten en cuenta que la Ecuación 8.11 también se puede usar para un condensador vacío configurando $κ = 1$. En otras palabras, podemos decir que la constante dieléctrica del vacío es $1$, que es un valor de referencia.
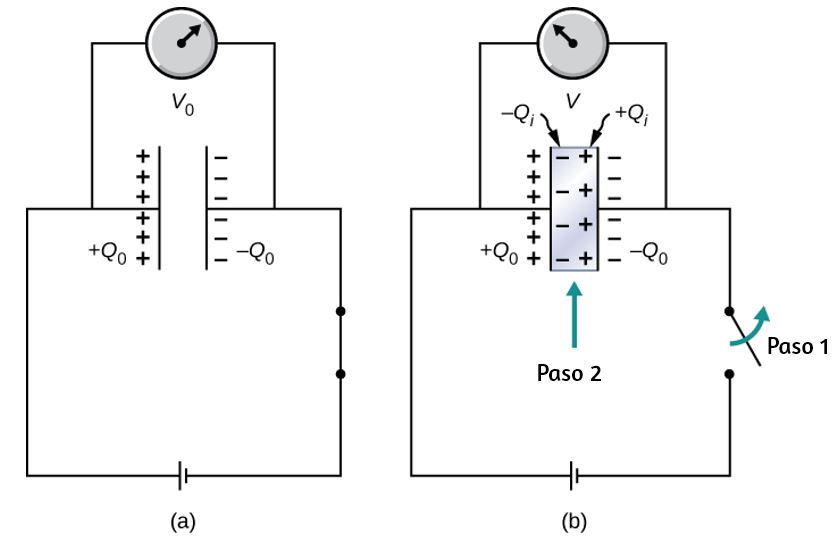
El principio expresado por la Ecuación 8.11 es ampliamente utilizado en la industria de la construcción (). Las placas de metal en un buscador de vigas electrónicas actúan efectivamente como un condensador. Coloca un buscador de vigas con su lado plano en la pared y lo mueve continuamente en la dirección horizontal. Cuando el buscador se mueve sobre un perno de madera, la capacitancia de sus placas cambia, porque la madera tiene una constante dieléctrica diferente que una pared de yeso. Este cambio desencadena una señal en un circuito y, por lo tanto, se detecta el espárrago.
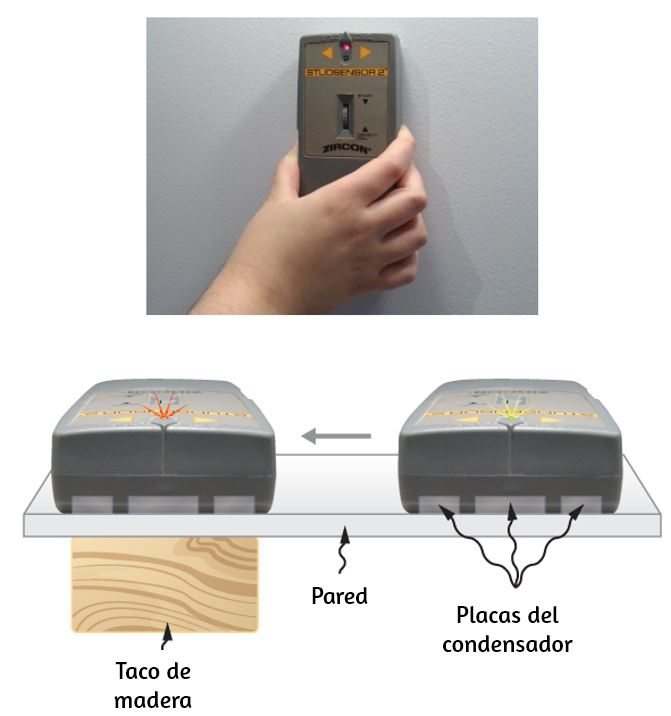
La energía eléctrica almacenada por un condensador también se ve afectada por la presencia de un dieléctrico. Cuando la energía almacenada en un condensador vacío es $U_0$, la energía $U$ almacenada en un condensador con un dieléctrico es más pequeña por un factor $κ$,
Cuando una muestra de material dieléctrico se acerca a un condensador cargado vacío, reacciona al campo eléctrico de las cargas en las placas del condensador. Habrá cargas inducidas en la superficie de la muestra; sin embargo, no son cargas libres como en un conductor, porque un aislante perfecto no tiene cargas que se muevan libremente. Estas cargas inducidas en la superficie dieléctrica son de signo opuesto a las cargas libres en las placas del condensador, y por lo tanto son atraídas por las cargas libres en las placas. En consecuencia, el dieléctrico se "arroja" hacia el hueco, y el trabajo para polarizar el material dieléctrico entre las placas se realiza a expensas de la energía eléctrica almacenada, que se reduce, de acuerdo con la ecuación 8.12.
Ejemplo 8.10
Insertar un dieléctrico en un condensador aislado
Un capacitor vacío de $20.0 pF$ se carga a una diferencia de potencial de $40.0 V$. La batería de carga se desconecta y se inserta una pieza de Teflon™ con una constante dieléctrica de 2.1 para llenar completamente el espacio entre las placas del condensador (consulta la ).
¿Cuáles son los valores de (a) la capacitancia, (b) la carga de la placa, (c) la diferencia de potencial entre las placas, y (d) la energía almacenada en el condensador con y sin dieléctrico?
Estrategia
Identificamos la capacitancia original $C_0 = 20.0 pF$ y la diferencia de potencial original $V_0 = 40.0 V$ entre las placas. Combinamos la Ecuación 8.11 con otras relaciones que involucran la capacitancia y el sustituto.
Solución
a. La capacitancia aumenta a
$$C = κC_0 = 2.1(20.0 pF) = 42.0 pF.$$b. Sin dieléctrico, la carga en las placas es
$$Q_0 = C_0V_0 = (20.0 pF)(40.0 V) = 0.8 nC.$$c. Como la batería está desconectada antes de insertar el dieléctrico, la carga de la placa no se ve afectada por el dieléctrico y permanece a $0.8 nC$.
Con el dieléctrico, la diferencia de potencial se vuelve
$$V = \frac{1}{κ}V_0 = \frac{1}{2.1}40.0 V = 19.0 V.$$d. La energía almacenada sin el dieléctrico es
$$U_0 = \frac{1}{2}C_0V_0^2 = \frac{1}{2}(20.0 pF)(40.0 V)^2 = 16.0 nJ.$$Con el dieléctrico insertado, usamos la Ecuación 8.12 para encontrar que la energía almacenada disminuye a
$$U = \frac{1}{κ}U_0 = \frac{1}{2.1}16.0 nJ = 7.6 nJ.$$Explicación
Observa que el efecto de un dieléctrico en la capacitancia de un condensador es un aumento drástico de su capacitancia. Este efecto es mucho más profundo que un simple cambio en la geometría de un condensador.
 Comprueba tu aprendizaje 8.7
Comprueba tu aprendizaje 8.7
Podemos entender el efecto de un dieléctrico en la capacitancia observando su comportamiento a nivel molecular. Como hemos visto en capítulos anteriores, en general, todas las moléculas se pueden clasificar como polares o no polares. Existe una separación neta de cargas positivas y negativas en una molécula polar aislada, mientras que no hay separación de carga en una molécula no polar aislada ().
En otras palabras, las moléculas polares tienen momentos dipolares eléctricos permanentes y las moléculas no polares no. Por ejemplo, una molécula de agua es polar, y una molécula de oxígeno es no polar. Las moléculas no polares pueden volverse polares en presencia de un campo eléctrico externo, lo que se denomina polarización inducida.
Consideremos primero un dieléctrico compuesto de moléculas polares. En ausencia de cualquier campo eléctrico externo, los dipolos eléctricos están orientados aleatoriamente, como se ilustra en la (a). Sin embargo, si el dieléctrico se coloca en un campo eléctrico externo $\overrightarrow{\bold{E}}_0$, las moléculas polares se alinean con el campo externo, como se muestra en la parte (b) de la figura.
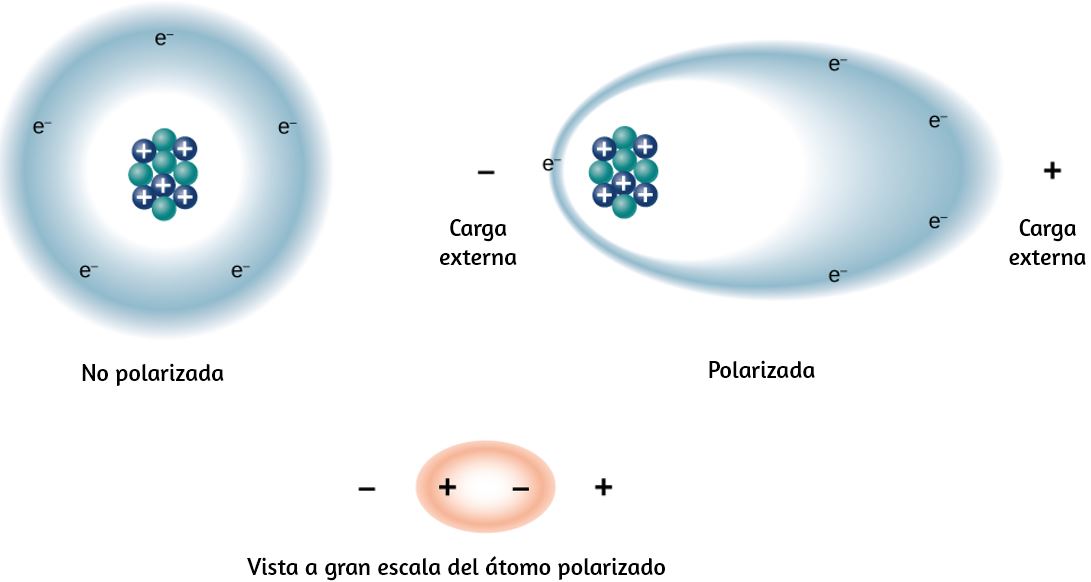
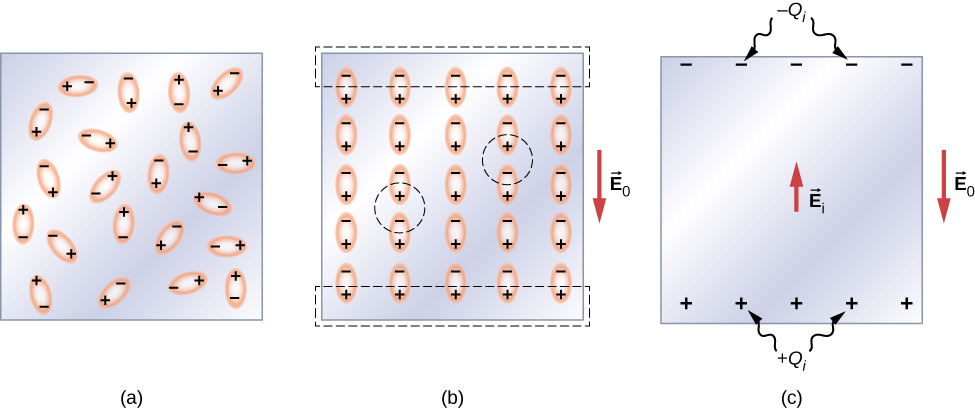
Las cargas opuestas en los dipolos adyacentes dentro del volumen del dieléctrico se neutralizan entre sí, por lo que no hay carga neta dentro del dieléctrico (ver los círculos discontinuos en la parte (b)). Sin embargo, este no es el caso muy cerca de las superficies superior e inferior que bordean el dieléctrico (la región encerrada por los rectángulos punteados en la parte (b)), donde la alineación produce una carga neta. Dado que el campo eléctrico externo simplemente alinea los dipolos, el dieléctrico como un todo es neutral, y las cargas superficiales inducidas en sus caras opuestas son iguales y opuestas. Estas cargas superficiales inducidas $+Q_i$ y $-Q_i$ producen un campo eléctrico adicional $\overrightarrow{\bold{E}}_i$ (un campo eléctrico inducido), que se opone al campo externo $\overrightarrow{\bold{E}}_0$, como se ilustra en la parte (c).
El mismo efecto se produce cuando las moléculas de un dieléctrico son no polares. En este caso, una molécula no polar adquiere un momento dipolar eléctrico inducido porque el campo externo $\overrightarrow{\bold{E}}_0$ provoca una separación entre sus cargas positiva y negativa. Los dipolos inducidos de las moléculas no polares se alinean con $\overrightarrow{\bold{E}}_0$ de la misma manera que los dipolos permanentes de las moléculas polares están alineados (se muestra en la parte (b)). Por lo tanto, el campo eléctrico dentro del dieléctrico se debilita independientemente de si sus moléculas son polares o no polares.
Por lo tanto, cuando la región entre las placas paralelas de un condensador cargado, como la que se muestra en la (a), se llena con un dieléctrico, dentro del dieléctrico hay un campo eléctrico $\overrightarrow{\bold{E}}_0$ debido a la carga libre $Q_0$ en las placas del condensador y un campo eléctrico $\overrightarrow{\bold{E}}_i$ debido a la carga inducida $Q_i$ en las superficies del dieléctrico. Su suma vectorial proporciona el campo eléctrico neto $\overrightarrow{\bold{E}}$ dentro del dieléctrico entre las placas del condensador (que se muestra en la parte (b) de la figura):
Se puede considerar que este campo de red es el campo producido por una carga efectiva $Q_0 - Q_i$ en el condensador.
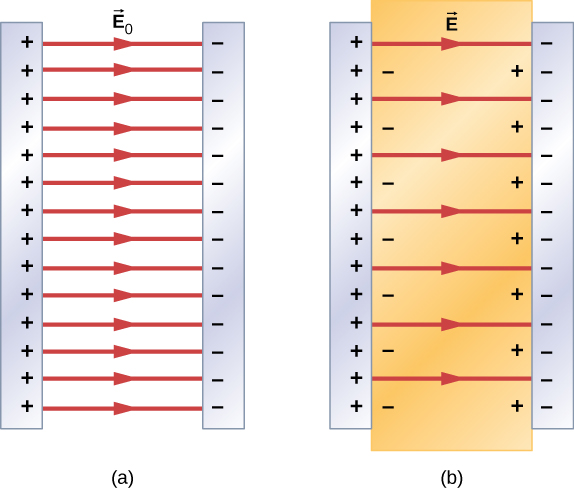
En la mayoría de los dieléctricos, el campo eléctrico neto $\overrightarrow{\bold{E}}$ es proporcional al campo $\overrightarrow{\bold{E}}_0$ producido por la carga libre. En términos de estos dos campos eléctricos, la constante dieléctrica $κ$ del material se define como
Como $\overrightarrow{\bold{E}}_0$ y $\overrightarrow{\bold{E}}$ apuntan en direcciones opuestas, la magnitud $E$ es menor que la magnitud $E_0$ y, por lo tanto, $κ > 1$. La combinación de la Ecuación 8.14 con la Ecuación 8.13 y la reorganización de los términos, produce la siguiente expresión para el campo eléctrico inducido en un dieléctrico:
Cuando la magnitud de un campo eléctrico externo se vuelve demasiado grande, las moléculas del material dieléctrico comienzan a ionizarse. Una molécula o un átomo se ioniza cuando uno o más electrones se eliminan de él y se convierten en electrones libres, ya no se unen a la estructura molecular o atómica. Cuando esto sucede, el material puede conducir, lo que permite que la carga se mueva a través del dieléctrico de una placa de condensador a la otra. Este fenómeno se llama ruptura dieléctrica (La Figura 8.1 muestra patrones típicos de trayectoria aleatoria de descarga eléctrica durante la ruptura dieléctrica). El valor crítico, $E_c$, del campo eléctrico al que se ionizan las moléculas de un aislador se denomina resistencia dieléctrica del material.
La resistencia dieléctrica impone un límite en la tensión que se puede aplicar para una separación de placas dada en un condensador. Por ejemplo, la resistencia dieléctrica del aire es $E_c = 3.0 MV/m$, por lo que para un condensador lleno de aire con una separación de placa de $d = 1.00 mm$, el límite en la diferencia de potencial que se puede aplicar de manera segura a través de sus placas sin causar una ruptura dieléctrica es $V = E_cd = (3.0 × 10^6 V/m)(1.00 × 10^{-3} m) = 3.0 kV$.
Sin embargo, este límite se convierte en $60.0 kV$ cuando el mismo capacitor se llena con Teflon™, cuya resistencia dieléctrica es de aproximadamente $60.0 MV/m$. Debido a este límite impuesto por la resistencia dieléctrica, la cantidad de carga que puede almacenar un condensador lleno de aire es solo $Q_0 = κ_{\textsf{aire}}C_0(3.0 kV)$ y la carga almacenada en el mismo capacitor lleno de Teflon™ puede ser tanto como
$$\begin{split} Q &= κ_{\textsf{teflón}}C_0(60.0 kV) = κ_{\textsf{teflón}}\frac{Q_0}{κ_{\textsf{aire}}(3.0 kV)}(60.0 kV) \\ &= 20\frac{κ_{\textsf{teflón}}}{κ_{\textsf{aire}}}Q_0 = 20\frac{2.1}{1.00059}Q_0 ≅ 42Q_0 \end{split}$$que es aproximadamente 42 veces mayor que una carga almacenada en un condensador lleno de aire. Los valores típicos de las constantes dieléctricas y las resistencias dieléctricas para diversos materiales se dan en la . Observa que la constante dieléctrica $κ$ es exactamente $1,0$ para el vacío (el espacio vacío sirve como condición de referencia) y muy cerca de $1,0$ para el aire en condiciones normales (presión normal a temperatura ambiente). Estos dos valores están tan cerca que, de hecho, las propiedades de un condensador lleno de aire son esencialmente las mismas que las de un condensador vacío.
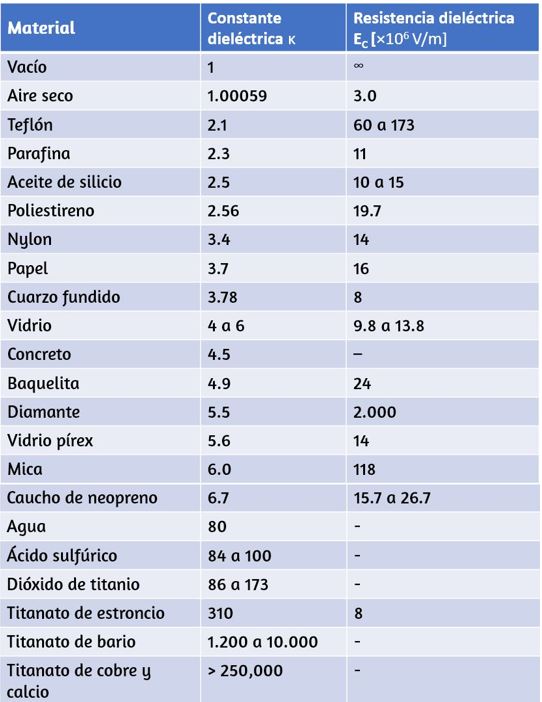
No todas las sustancias enumeradas en la tabla son buenos aislantes, a pesar de sus altas constantes dieléctricas. El agua, por ejemplo, consiste en moléculas polares y tiene una gran constante dieléctrica de aproximadamente 80. En una molécula de agua, es más probable que se encuentren electrones alrededor del núcleo de oxígeno que alrededor de los núcleos de hidrógeno. Esto hace que el extremo del oxígeno de la molécula sea ligeramente negativo y deja los hidrógenos al final ligeramente positivos, lo que hace que la molécula se alinee fácilmente a lo largo de un campo eléctrico externo y, por lo tanto, el agua tiene una gran constante dieléctrica. Sin embargo, la naturaleza polar de las moléculas de agua también hace que el agua sea un buen solvente para muchas sustancias, lo que produce efectos indeseables, ya que cualquier concentración de iones libres en el agua conduce la electricidad.
Ejemplo 8.11
Campo eléctrico y carga de superficial inducida
Supongamos que la distancia entre las placas del condensador en el ejemplo 8.10 es de $2.0 mm$ y el área de cada placa es de $4.5 × 10^{-3} m^2$. Determina: (a) el campo eléctrico entre las placas antes y después de insertar el Teflon™, y (b) la carga superficial inducida en las superficies de Teflon™.
Estrategia
En la parte (a), sabemos que el voltaje en el condensador vacío es $V_0 = 40 V$, por lo que para encontrar los campos eléctricos usamos la relación $V = Ed$ y la Ecuación 8.14. En la parte (b), conociendo la magnitud del campo eléctrico, usamos la expresión para la magnitud del campo eléctrico cerca de una placa cargada $E = σ/ε_0$, donde σ es una densidad de carga superficial uniforme causada por la carga superficial. Usamos el valor de la carga libre $Q_0 = 8.0 × 10^{-10} C$ obtenida en el Ejemplo 8.10.
Solución
a. El campo eléctrico $E^2$ entre las placas de un condensador vacío es
$$E_0 = \frac{V_0}{d} = (40 V)/(2.0 × 10^{-3} m) = 2.0 × 10^4 V/m$$El campo eléctrico E con el Teflon™ en su lugar es
$$E = \frac{1}{κ}E_0 = \frac{1}{2.1}2.0 × 10^4 V/m = 9.5 × 10^3 V/m$$b. La carga efectiva en el condensador es la diferencia entre la carga libre $Q_0$ y la carga inducida $Q_i$. El campo eléctrico en el Teflon™ es causado por esta carga efectiva. Así
$$E = \frac{1}{ε_0}σ = \frac{1}{ε_0}\frac{Q_0 - Q_i}{A}$$Invertimos esta ecuación para obtener $Q_i$,
$$\begin{split} Q_i &= Q_0 - ε_0AE \\ &= {\footnotesize 8.0 × 10^{-10} C − (8.85 × 10^{-12} C^2/(N \cdot m^2))(4.5 × 10^{-3} m^2)(9.5 × 10^3 V/m)} \\ &= 4.2 × 10^{-10} C = 0.42 nC \end{split}$$Ejemplo 8.12
Insertar un dieléctrico en un condensador conectado a una batería
Una batería de voltaje $V_0$ está conectada a través de un condensador vacío de capacitancia $C_0$, la carga en sus placas es $Q_0$, y el campo eléctrico entre ellas es $E_0$.
Se inserta un dieléctrico de constante dieléctrica $κ$ entre las placas mientras la batería permanece en su lugar, como se muestra en la . (a) Encuentra la capacitancia $C$, la tensión $V$ a través del condensador y el campo eléctrico $E$ entre las placas después de insertar el dieléctrico. (b) Obtén una expresión para la carga libre $Q$ en las placas del condensador lleno y la carga inducida $Q_i$ en la superficie dieléctrica en términos de la carga $Q_0$ de la placa original.
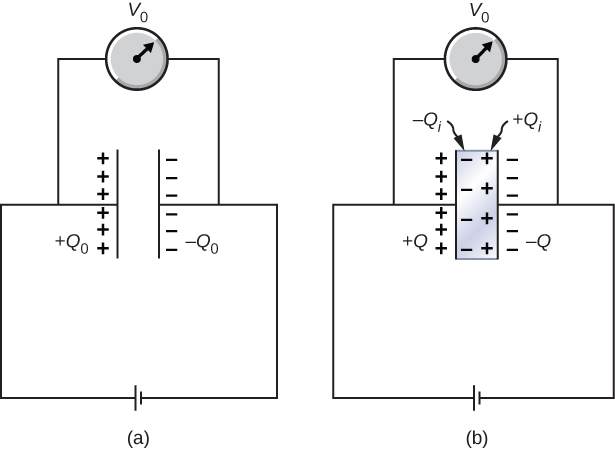
Estrategia
Identificamos los valores conocidos: $V_0$, $C_0$, $E_0$, $κ$ y $Q_0$. Nuestra tarea es expresar los valores desconocidos en términos de estos valores conocidos.
Solución
(a) La capacitancia del condensador lleno es $C = κC_0$. Como la batería siempre está conectada a las placas del condensador, la diferencia de potencial entre ellas no cambia; por lo tanto, $V = V_0$. Debido a eso, el campo eléctrico en el condensador lleno es el mismo que el campo en el condensador vacío, por lo que podemos obtenerlo directamente
$$E = \frac{V}{d} = \frac{V_0}{d} = E_0$$(b) Para el condensador lleno, la carga libre en las placas es
$$Q = CV = (κC_0)V_0 = κ(C_0V_0) = κQ_0.$$El campo eléctrico E en el condensador lleno se debe a la carga efectiva $Q - Q_i$ ( (b)). Como $E = E_0$, tenemos
$$\frac{Q - Q_i}{ε_0A}$$Resolviendo esta ecuación para $Q_i$, obtenemos la carga inducida
$$Q_i = Q - Q_0 = κQ_0 - Q_0 = (κ - 1)Q_0.$$Explicación
Observa que para materiales con constantes dieléctricas mayores que $2$ (ver ), la carga inducida en la superficie del dieléctrico es mayor que la carga en las placas de un condensador de vacío. Lo opuesto es cierto para los gases como el aire cuya constante dieléctrica es menor que $2$.
 Comprueba tu aprendizaje 8.8
Comprueba tu aprendizaje 8.8
 Comprueba tu aprendizaje 8.9
Comprueba tu aprendizaje 8.9
En el siguiente vídeo, un condensador ajustable de placa paralela se mantiene a un voltaje constante. A medida que la separación entre las placas se ensancha, el electrómetro muestra la carga que fluye de las placas, mientras que el electroscopio no muestra cambios en el voltaje. Observa (por la deflexión de la aguja) que fluye más carga de las placas cuando están más juntas, y menos cuando están más separadas. Cuando las placas se vuelven a juntar, vemos que la carga fluye hacia atrás sobre las placas. Luego, depositamos una cantidad fija de carga en la placa izquierda. Ahora, cuando la separación se amplía, el electroscopio muestra un voltaje en aumento, incluso cuando la cantidad de carga permanece constante. Cuando se inserta un bloque de plexiglass (un dieléctrico) entre las placas, el voltaje cae. Sin embargo, cuando se quita el plexi, el voltaje sube nuevamente, mostrando que la carga todavía está allí. Esta es una de las razones principales por las que los condensadores se construyen con dieléctricos entre sus placas; más carga se puede almacenar a un voltaje más bajo.
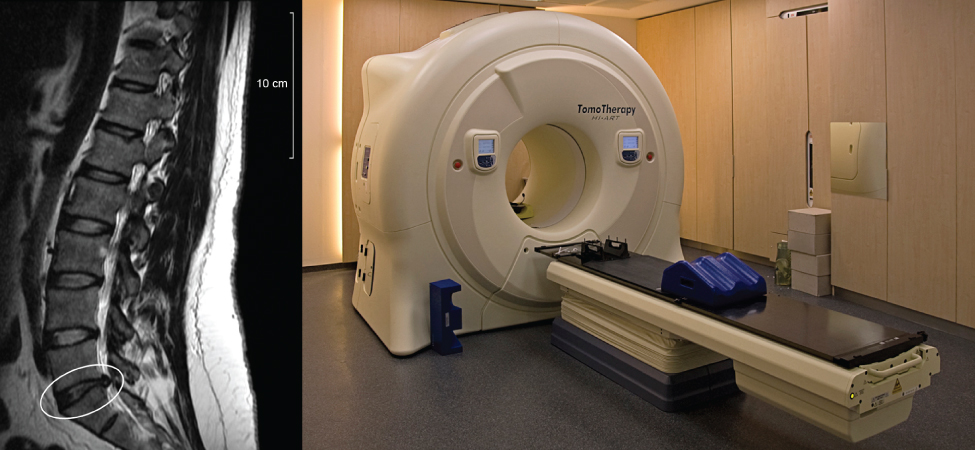
En este capítulo, estudiaremos la corriente eléctrica a través de un material, donde la corriente eléctrica es la tasa de flujo de carga. También examinamos una característica de los materiales conocidos como la resistencia. La resistencia es una medida de cuánto impide un material el flujo de carga, y se mostrará que la resistencia depende de la temperatura. En general, un buen conductor, como el cobre, el oro o la plata, tiene una resistencia muy baja. Algunos materiales, llamados superconductores, tienen resistencia cero a temperaturas muy bajas.
Se requieren altas corrientes para la operación de electroimanes. Los superconductores se pueden usar para fabricar electroimanes que son $10$ veces más fuertes que los electroimanes convencionales más fuertes.
Estos imanes superconductores se utilizan en la construcción de dispositivos de imágenes de resonancia magnética (MRI) que se pueden usar para hacer imágenes de alta resolución del cuerpo humano. La imagen de apertura de capítulo muestra una imagen MRI de las vértebras de un sujeto humano y el dispositivo de MRI en sí. Los imanes superconductores tienen muchos otros usos. Por ejemplo, los imanes superconductores se utilizan en el Gran Colisionador de Hadrones (LHC) para curvar la trayectoria de los protones en el anillo.
Hasta ahora, hemos considerado principalmente cargas estáticas. Cuando las cargas se movieron, se aceleraron en respuesta a un campo eléctrico creado por una diferencia de voltaje. Las cargas perdieron energía potencial y ganaron energía cinética mientras viajaban a través de una diferencia de potencial donde el campo eléctrico funcionaba con la carga.
Aunque las cargas no requieren la transmisión de un material, la mayoría de este capítulo trata sobre la comprensión del movimiento de cargas a través de un material. La velocidad a la que las cargas pasan por una ubicación, es decir, la cantidad de carga por unidad de tiempo, se conoce como corriente eléctrica. Cuando las cargas fluyen a través de un medio, la corriente depende del voltaje aplicado, el material a través del cual fluyen las cargas y el estado del material. De particular interés es el movimiento de cargas en un cable conductor.
En capítulos anteriores, las cargas se aceleraron debido a la fuerza proporcionada por un campo eléctrico, la pérdida de energía potencial y la obtención de energía cinética. En este capítulo, discutimos la situación de la fuerza proporcionada por un campo eléctrico en un conductor, donde las cargas pierden energía cinética para el material que alcanza una velocidad constante, conocida como la "velocidad de deriva".
Esto es análogo a un objeto que cae a través del atmósfera y pierde energía cinética en el aire, alcanzando una velocidad terminal constante.
Si alguna vez tomaste un curso de primeros auxilios o de seguridad, es posible que hayas escuchado que, en caso de choque eléctrico, es la corriente, no el voltaje, el factor importante en la gravedad del choque y la cantidad de daño al cuerpo humano. La corriente se mide en unidades llamadas amperios; Es posible que hayas notado que los interruptores automáticos en tu hogar y los fusibles en tu automóvil están clasificados en amperios. Pero, ¿qué es el amperio y qué mide?
La corriente eléctrica se define como la velocidad a la cual fluye la carga. Cuando hay una gran corriente presente, como la que se utiliza para hacer funcionar un refrigerador, una gran cantidad de carga se mueve a través del cable en un período de tiempo pequeño. Si la corriente es pequeña, como la que se utiliza para operar una calculadora de mano, una pequeña cantidad de carga se mueve a través del circuito durante un largo período de tiempo.
La unidad del SI para la corriente es el amperio ($A$), llamado así por el físico francés André-Marie Ampère (1775-1836). Como $I = \frac{ΔQ}{Δt}$, vemos que un amperio se define como un culombio de carga que pasa a través de un área determinada por segundo:
$$1 A ≡ 1 \frac{C}{s} \tag{9.2}$$La corriente eléctrica instantánea, o simplemente la corriente eléctrica, es la derivada en el tiempo de la carga que fluye y se encuentra tomando el límite de la corriente eléctrica promedio como $Δt → 0$:
$$I = \lim_{Δt→0} \frac{ΔQ}{Δt} = \frac{dQ}{dt} \tag{9.3}$$La mayoría de los electrodomésticos están clasificados en amperios necesarios para una operación adecuada, como lo son los fusibles y los interruptores automáticos.
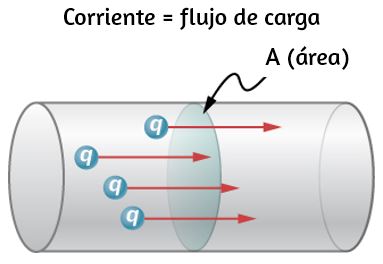
Ejemplo 9.1
Cálculo de la corriente promedio
El objetivo principal de una batería en un automóvil o camión es hacer funcionar el motor de arranque eléctrico, que enciende el motor. La operación de arranque del vehículo requiere que la batería suministre una gran cantidad de corriente. Una vez que el motor arranca, un dispositivo llamado alternador se encarga de suministrar la energía eléctrica requerida para el funcionamiento del vehículo y para cargar la batería.
(a) ¿Cuál es la corriente promedio involucrada cuando la batería de un camión pone en movimiento $720 C$ de carga en $4.00 s$ al encender un motor? (b) ¿Cuánto tiempo tarda en fluir $1,00 C$ de carga de la batería?
Estrategia
Podemos usar la definición de la corriente promedio en la ecuación $I = \frac{ΔQ}{Δt}$ para encontrar la corriente promedio en la parte (a), ya que se dan la carga y el tiempo. Para la parte (b), una vez que conocemos la corriente promedio, podemos definir su $I = \frac{ΔQ}{Δt}$ para encontrar el tiempo requerido para que fluya $1,00 C$ de carga de la batería.
Solución
a. Con los valores dados de carga y el tiempo en la definición de corriente, tenemos
$$I = \frac{ΔQ}{Δt} = \frac{720 C}{4.00 s} = 180 C/s = 180 A$$b. Resolviendo la relación $I = ΔQ/Δt$ para el tiempo $Δt$ e con los valores conocidos de carga y corriente, obtenemos:
$$Δt = \frac{ΔQ}{I} = \frac{1.00 C}{180 C/s} = 5.56 × 10^{−3} s = 5.5 6ms$$Explicación
a. Este gran valor para la corriente ilustra el hecho de que una carga grande se mueve en una pequeña cantidad de tiempo. Las corrientes en estos "motores de arranque" son bastante grandes para vencer la inercia del motor.
b. Una corriente alta requiere poco tiempo para suministrar una gran cantidad de carga. Esta gran corriente es necesaria para suministrar la gran cantidad de energía necesaria para arrancar el motor.
Ejemplo 9.2
Cálculo de corrientes instantáneas
Considera una carga que se mueve a través de una sección transversal de un cable donde la carga se modela como $Q(t) = Q_M(1 - e^{-t/τ})$. Aquí, $Q_M$ es la carga después de un largo período de tiempo, a medida que el tiempo se aproxima al infinito, con unidades de culombios, y τ es una constante de tiempo con unidades de segundos (consulta la ). ¿Cuál es la corriente a través del cable?
Estrategia
La corriente a través de la sección transversal se puede encontrar desde $I = \frac{dQ}{dt}$. Observa en la figura que la carga aumenta a $Q_M$ y la derivada disminuye, acercándose a cero, a medida que aumenta el tiempo ().
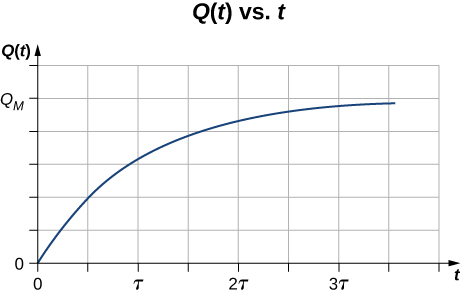
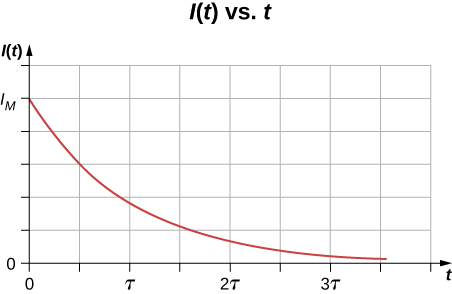
Solución
La derivada se puede encontrar usando $\frac{d}{dx}e^u = e^u\frac{du}{dx}$.
$$I = \frac{dQ}{dt} = \frac{d}{dt}[Q_M(1 - e^{-t/τ})] = \frac{Q_M}{τ}e^{-t/τ}$$Explicación
La corriente a través del cable en cuestión disminuye exponencialmente, como se muestra en la . En capítulos posteriores, se mostrará que una corriente dependiente del tiempo aparece cuando un condensador se carga o se descarga a través de una resistencia. Recuerda que un condensador es un dispositivo que almacena carga.
 Comprueba tu aprendizaje 9.1
Comprueba tu aprendizaje 9.1
 Comprueba tu aprendizaje 9.2
Comprueba tu aprendizaje 9.2
En los párrafos anteriores, definimos la corriente como la carga que fluye a través de un área de sección transversal por unidad de tiempo. Para que la carga fluya a través de un dispositivo, como el faro que se muestra en la , debe haber una ruta completa (o circuito) desde el terminal positivo al terminal negativo. Considera un circuito simple de una batería de automóvil, un interruptor, una lámpara de faro y cables que proporcionan una ruta de corriente entre los componentes. Para que la lámpara se encienda, debe haber una ruta completa para el flujo de corriente. En otras palabras, una carga debe poder dejar el terminal positivo de la batería, viajar a través del componente y regresar al terminal negativo de la batería. El interruptor está ahí para controlar el circuito. La parte (a) de la figura muestra el circuito simple de una batería de automóvil, un interruptor, una ruta de conducción y una lámpara de faro. También se muestra el esquema del circuito [parte (b)]. Un esquema es una representación gráfica de un circuito y es muy útil para visualizar las características principales de un circuito. Los esquemas usan símbolos estandarizados para representar los componentes en un circuito y líneas continuas para representar los cables que conectan los componentes. La batería se muestra como una serie de líneas largas y cortas, que representan la pila voltaica histórica. La lámpara se muestra como un círculo con un bucle dentro, que representa el filamento de una bombilla incandescente. El interruptor se muestra como dos puntos con una barra conductora para conectar los dos puntos y los cables que conectan los componentes se muestran como líneas continuas. El esquema de la parte (c) muestra la dirección del flujo de corriente cuando el interruptor está cerrado.
Cuando se cierra el interruptor en la (c), hay una ruta completa para que fluyan las cargas, desde el terminal positivo de la batería, a través del interruptor, luego a través del faro y de regreso al terminal negativo de la batería.
Ten en cuenta que la dirección del flujo de corriente es de positiva a negativa. La dirección de la corriente convencional siempre se representa en la dirección en que fluirá la carga positiva, desde el terminal positivo al terminal negativo.
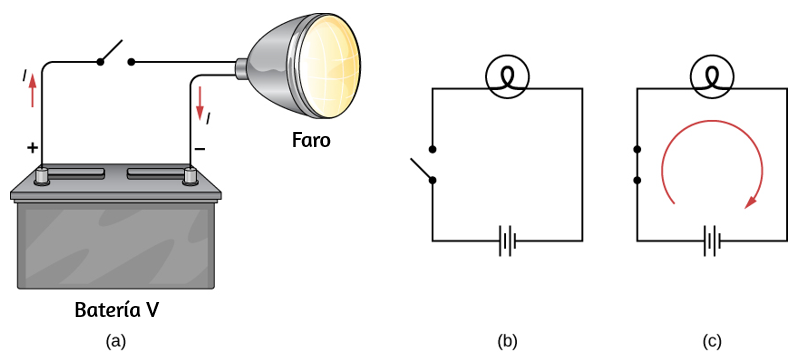
A continuación, presentamos una escena interactiva tomada del Proyecto @prende.mx, en la que podrás observar la diferencia de la corriente convencional con la electrónica.
Haz clic en los botones de la escena
La corriente convencional fluye desde el terminal positivo al terminal negativo, pero dependiendo de la situación real, las cargas positivas, negativas o ambas pueden moverse. En los cables de metal, por ejemplo, la corriente es transportada por electrones, es decir, se mueven las cargas negativas. En las soluciones iónicas, como el agua salada, se mueven las cargas positivas y negativas.
Esto también es cierto en las células nerviosas. Un generador Van de Graaff, usado para investigación nuclear, puede producir una corriente de cargas positivas puras, como protones. En el Acelerador de Tevatron en Fermilab, antes de que se cerrara en 2011, los haces de protones y antiprotones que viajaban en direcciones opuestas colisionaron. Los protones son positivos y, por lo tanto, su corriente está en la misma dirección en que viajan. Los antiprotones tienen carga negativa y, por lo tanto, su corriente está en la dirección opuesta a la que viajan las partículas reales.
Una mirada más cercana a la corriente que fluye a través de un cable se muestra en la . La figura ilustra el movimiento de partículas cargadas que componen una corriente. El hecho de que la corriente convencional se toma en la dirección en que fluiría la carga positiva se remonta al científico y estadista estadounidense Benjamin Franklin en el siglo XVIII. Al no tener conocimiento de las partículas que componen el átomo (a saber, el protón, el electrón y el neutrón), Franklin creía que la corriente eléctrica fluía de un material que tenía más de un "fluido eléctrico" y un material que tenía menos de este fluido eléctrico. Él acuñó el término positivo para el material que tenía más de este fluido eléctrico y negativo para el material que tenía menos fluido eléctrico. Él supuso que la corriente fluiría desde el material con más fluido eléctrico -el material positivo- hasta el material negativo. Franklin llamó a esta dirección de la corriente un flujo de corriente positiva. Este era un pensamiento bastante avanzado para un hombre que no sabía nada sobre el átomo.
Ahora sabemos que un material es positivo si tiene un mayor número de protones que electrones, y es negativo si tiene un mayor número de electrones que protones. En un metal conductor, el flujo de corriente se debe principalmente a los electrones que fluyen del material negativo al material positivo, pero por razones históricas, consideramos que el flujo de corriente positiva y la corriente fluyen desde el terminal positivo de la batería al terminal negativo.
Es importante darse cuenta de que un campo eléctrico está presente en los conductores y es responsable de producir la corriente (). En capítulos anteriores, consideramos el caso eléctrico estático, donde las cargas en un conductor se redistribuyen rápidamente en la superficie del conductor para cancelar el campo eléctrico externo y restablecer el equilibrio. En el caso de un circuito eléctrico, se previene que las cargas alcancen el equilibrio por una fuente externa de potencial eléctrico, tal como una batería. La energía necesaria para mover la carga es suministrada por el potencial eléctrico de la batería.
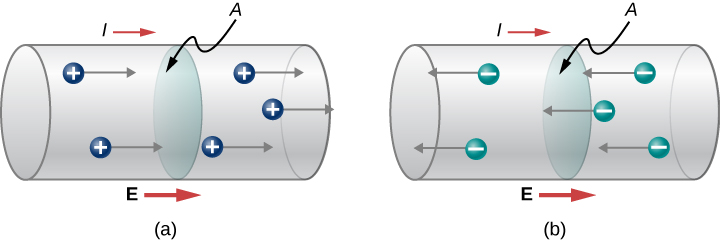
Aunque el campo eléctrico es responsable del movimiento de las cargas en el conductor, el trabajo realizado en las cargas por el campo eléctrico no aumenta la energía cinética de las cargas. Mostraremos que el campo eléctrico es responsable de mantener las cargas eléctricas en movimiento a una "velocidad de deriva".
Cuando los electrones se mueven a través de un cable conductor, no se mueven a una velocidad constante, es decir, los electrones no se mueven en línea recta a una velocidad constante. Por el contrario, interactúan y chocan con los átomos y otros electrones libres en el conductor. Por lo tanto, los electrones se mueven en zig-zag y se desplazan a través del cable. También debemos observar que, aunque es conveniente analizar la dirección de la corriente, la corriente es una cantidad escalar. Cuando se habla de la velocidad de las cargas en una corriente, es más apropiado analizar la densidad de corriente. Volveremos a esta idea al final de esta sección.
Las señales eléctricas se mueven muy rápido. Las conversaciones telefónicas llevadas por corrientes en cables cubren grandes distancias sin demoras notables. Las luces se encienden tan pronto como un interruptor de luz se mueve a la posición 'encendido'. La mayoría de las señales eléctricas transportadas por corrientes viajan a velocidades del orden de $108 m/s$, una fracción significativa de la velocidad de la luz. Curiosamente, las cargas individuales que componen el movimiento actual son mucho más lentas en promedio, generalmente a la deriva a velocidades del orden de $10^{-4} m/s$. ¿Cómo conciliamos estas dos velocidades y qué nos dice sobre los conductores estándar?
La alta velocidad de las señales eléctricas resulta del hecho de que la fuerza entre cargas actúa rápidamente a distancia. Por lo tanto, cuando se fuerza una carga libre en un cable, como en la , la carga entrante empuja otras cargas por delante debido a la fuerza de repulsión entre cargas similares. Estas cargas en movimiento empujan las cargas más abajo de la línea.
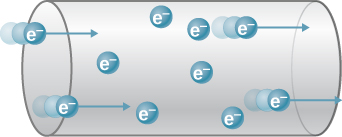
La densidad de carga en un sistema no puede aumentarse fácilmente, por lo que la señal se transmite rápidamente. La onda de choque eléctrica resultante se mueve a través del sistema casi a la velocidad de la luz. Para ser precisos, esta señal de movimiento rápido, u onda de choque, es un cambio que se propaga rápidamente en el campo eléctrico.
Los buenos conductores tienen una gran cantidad de cargas libres. En metales, las cargas libres son electrones libres (de hecho, los buenos conductores eléctricos también suelen ser buenos conductores de calor, porque un gran número de electrones libres pueden transportar energía térmica y transportar corriente eléctrica). La muestra cómo los electrones libres se mueven a través de un conductor ordinario. La distancia que puede mover un electrón individual entre colisiones con átomos u otros electrones es bastante pequeña. Los trayectos de electrones aparecen así casi al azar, como el movimiento de los átomos en un gas. Pero hay un campo eléctrico en el conductor que hace que los electrones se desvíen en la dirección que se muestra (frente al campo, ya que son negativos). La velocidad de deriva $\overrightarrow{\bold{v}}_d$ es la velocidad promedio de las cargas libres. La velocidad de deriva es bastante pequeña, ya que hay muchas cargas libres.
Si tenemos una estimación de la densidad de electrones libres en un conductor, podemos calcular la velocidad de deriva para una corriente dada. Cuanto mayor es la densidad, menor es la velocidad requerida para una corriente dada.
Las colisiones de electrones libres transfieren energía a los átomos del conductor. El campo eléctrico funciona moviendo los electrones a través de una distancia, pero ese trabajo no aumenta la energía cinética (ni la velocidad) de los electrones. El trabajo se transfiere a los átomos del conductor, a menudo aumentando la temperatura.
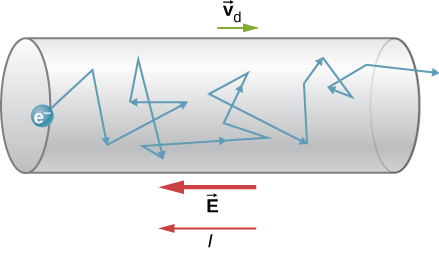
Por lo tanto, se requiere una entrada de potencia continua para mantener el flujo de la corriente (una excepción son los superconductores, que pueden tener una corriente constante sin un suministro continuo de energía, un gran ahorro de energía). Para un conductor que no es un superconductor, el suministro de energía puede ser útil, como en un filamento de bombilla incandescente ().
El suministro de energía es necesario para aumentar la temperatura del filamento de tungsteno, de modo que el filamento se ilumine.
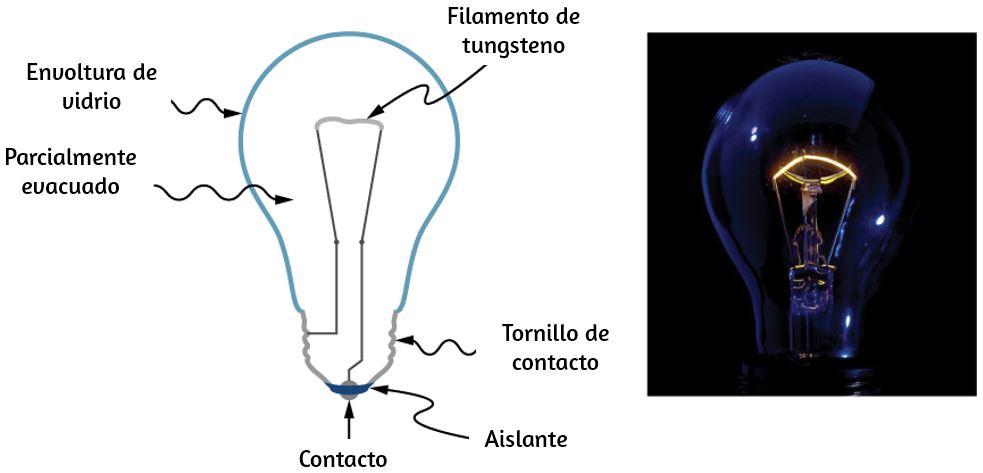
En la siguiente escena interactiva, diseñada por Loo Kang Wee, puedes cambiar parámetros como número de electrones, temperatura y campo eléctrico. Haz clic en el botón ejecutar y observa el movimiento de los electrones.
Podemos obtener una expresión para la relación entre la corriente y la velocidad de deriva al considerar el número de cargas libres en un segmento de cable, como se ilustra en la . El número de cargas libres por unidad de volumen, o el número de densidad de cargas libres, es dado por el símbolo $n$ donde $n = \frac{\textsf{número de cargas}}{\textsf{volumen}}$. El valor de $n$ depende del material. El segmento sombreado tiene un volumen $Av_ddt$, por lo que el número de cargas libres en el volumen es $nAv_ddt$. La carga $dQ$ en este segmento es, por lo tanto, $qnAv_ddt$, donde $q$ es la cantidad de carga (La magnitud de la carga de electrones es $q = 1.60 × 10^{-19} C$). La corriente es la carga movida por unidad de tiempo; por lo tanto, si todas las cargas originales se mueven fuera de este segmento a tiempo dt, la corriente es
$$I = \frac{dQ}{dt} = qnAv_d$$Reordenando los términos, obtenemos:
donde $v_d$ es la velocidad de deriva, $n$ es la densidad de carga libre, $A$ es el área de la sección transversal del cable, e $I$ es la corriente a través del cable. Los portadores de la corriente tienen cada uno carga $q$ y se mueven con una velocidad de deriva de magnitud $v_d$.
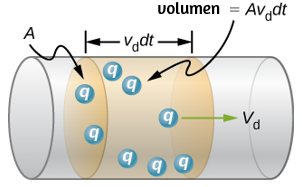
Ten en cuenta que la velocidad de deriva simple no es toda la historia. La velocidad de un electrón es a veces mucho mayor que su velocidad de deriva. Además, no todos los electrones en un conductor se pueden mover libremente, y los que se mueven pueden moverse un poco más rápido o más lento que la velocidad de deriva (observa, de nuevo, la escena interactiva anterior). Entonces, ¿qué queremos decir con electrones libres?
Los átomos en un conductor metálico están empaquetados en forma de una estructura de celosía. Algunos electrones están lo suficientemente lejos de los núcleos atómicos como para no experimentar la atracción de los núcleos tan fuertemente como lo hacen los electrones internos. Estos son los electrones libres. No están unidos a un solo átomo, sino que pueden moverse libremente entre los átomos en un "mar" de electrones. Cuando se aplica un campo eléctrico, estos electrones libres responden acelerando. A medida que se mueven, colisionan con los átomos de la red y con otros electrones, generando energía térmica, y el conductor se calienta. En un aislador, la organización de los átomos y la estructura no permiten esos electrones libres.
Como sabes, la energía eléctrica generalmente se suministra a los equipos y electrodomésticos a través de cables redondos hechos de un material conductor (cobre, aluminio, plata u oro). El diámetro del cable determina la capacidad de transporte de corriente: cuanto mayor es el diámetro, mayor es la capacidad de transporte de corriente. Aunque la capacidad de transporte de corriente está determinada por el diámetro, el cable normalmente no se caracteriza por el diámetro directamente. En cambio, el alambre se vende comúnmente en una unidad conocida como "calibre". Los alambres se fabrican pasando el material a través de formas circulares llamadas "moldes de trefilado".
Para fabricar alambres más delgados, los fabricantes dibujan los alambres a través de múltiples troqueles de diámetro sucesivamente más delgado. Históricamente, el calibre del cable estaba relacionado con la cantidad de procesos de dibujo necesarios para fabricar el cable. Por esta razón, cuanto mayor sea el calibre, menor será el diámetro. En los Estados Unidos, el American Wire Gauge (AWG) fue desarrollado para estandarizar el sistema. El cableado doméstico comúnmente consta de un cable de calibre $10$ ($2.588 mm$ de diámetro) a $14$ de calibre ($1.628 mm$ de diámetro).
En la se muestra un dispositivo utilizado para medir el calibre del cable.

Ejemplo 9.3
Cálculo de la velocidad de deriva en un cable común
Calcula la velocidad de deriva de los electrones en un cable de cobre con un diámetro de $2.053 mm$ (calibre $12$) con una corriente de $20.0 A$, dado que hay un electrón libre por átomo de cobre (El cableado doméstico a menudo contiene cable de cobre calibre $12$, y la corriente máxima permitida en dicho cable suele ser de $20,0 A$). La densidad del cobre es de $8,80 × 10^3 kg/m^3$ y la masa atómica de cobre es de $63,54 g/mol$.
Estrategia
Podemos calcular la velocidad de deriva usando la ecuación $I = nqAv_d$. La corriente es $I = 20.00 A y q = 1.60 × 10^{-19} C$ es la carga de un electrón. Podemos calcular el área de una sección transversal del cable usando la fórmula $A = πr^2$, donde $r$ es la mitad del diámetro. El diámetro dado es $2.053 mm$, entonces $r$ es $1.0265 mm$. Nos dan la densidad del cobre, $8.80 × 10^3 kg/m^3$, y la masa atómica del cobre es $63.54 g/mol$.
Podemos usar estas dos cantidades junto con el número de Avogadro, $6.02 × 10^{23} atom/mol$, para determinar $n$, la cantidad de electrones libres por metro cúbico.
Solución
Primero, calculamos la densidad de electrones libres en cobre. Hay un electrón libre por átomo de cobre. Por lo tanto, el número de electrones libres es el mismo que el número de átomos de cobre por $m^3$. Ahora, podemos encontrar $n$ de la siguiente manera:
El área de la sección transversal del cable es
$$A = πr^2 = π(2.05 × 10^{-3} m/2)^2 = 3.30 × 10^{-6} m^2$$Reordenando $I = nqAv_d$ para aislar la velocidad de deriva, obtenemos:
$$\begin{split} v_d &= \frac{I}{nqA} \\ &= 20.00 A/(8.34× 0^{28}/m^3)(−1.60×10^{-19} C)(3.30× 0^{-6} m^2) \\ &= −4.54 × 10^{-4} m/s \end{split}$$Explicación
El signo menos indica que las cargas negativas se mueven en la dirección opuesta a la corriente convencional.
El pequeño valor para la velocidad de deriva (del orden de $10^{-4} m/s$) confirma que la señal se mueve en el orden de $10^{12}$ veces más rápido (alrededor de $108 m/s$) que las cargas que lo transportan.
 Comprueba tu aprendizaje 9.3
Comprueba tu aprendizaje 9.3
Aunque a menudo es conveniente adjuntar un signo negativo o positivo para indicar la dirección general del movimiento de las cargas, la corriente es una cantidad escalar, $I = \frac{dQ}{dt}$. A menudo es necesario discutir los detalles del movimiento de una carga, en lugar de discutir el movimiento general de las cargas. En tales casos, es necesario analizar la densidad de corriente, $\overrightarrow{\bold{J}}$, una cantidad vectorial. La densidad de corriente es el flujo de carga a través de un área infinitesimal, dividida por el área. La densidad de corriente debe tener en cuenta la magnitud de la corriente y la dirección del flujo de carga, que varía de un punto a otro. La unidad de densidad de corriente es el amperio por metro cuadrado, y la dirección se define como la dirección del flujo neto de cargas positivas a través del área.
La relación entre la densidad de corriente y la corriente se puede ver en la . El flujo de corriente diferencial a través del área $d\overrightarrow{\bold{A}}$ se encuentra como
$$dI = \overrightarrow{\bold{J}} \cdot d\overrightarrow{\bold{A}} = JdAcosθ$$donde $θ$ es el ángulo entre el área y la densidad de corriente. La corriente total que pasa por el área $d\overrightarrow{\bold{A}}$ se puede encontrar al integrarse con respecto al área,
Considera que la magnitud de la densidad de corriente, es la corriente dividida por el área:
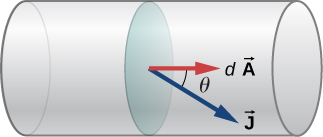
Por lo tanto, la densidad de corriente es $\overrightarrow{\bold{J}} = nq\overrightarrow{\bold{v}}_d$. Si q es positivo, $\overrightarrow{\bold{v}}_d$ está en la misma dirección que el campo eléctrico $\overrightarrow{\bold{E}}$. Si $q$ es negativo, $\overrightarrow{\bold{v}}_d$ está en la dirección opuesta a $\overrightarrow{\bold{E}}$.
De cualquier manera, la dirección de la densidad de corriente $\overrightarrow{\bold{J}}$ está en la dirección del campo eléctrico $\overrightarrow{\bold{E}}$
Ejemplo 9.4
Cálculo de la densidad de corriente en un cable
La corriente suministrada a una lámpara con una bombilla de $100 W$ es de $0,87$ amperios. La lámpara está cableada con un cable de cobre con un diámetro de $2.588 mm$ (calibre $10$). Encuentra la magnitud de la densidad de corriente.
Estrategia
La densidad de corriente es la corriente que se mueve a través de un área infinitesimal de sección transversal dividida por el área. Podemos calcular la magnitud de la densidad de corriente usando $J = I/A$. La corriente se da como $0.87 A$. El área de la sección transversal puede calcularse como $A = 5.26 mm^2$.
Solución
Calcula la densidad de corriente usando la corriente dada $I = 0.87 A$ y el área, que es $A = 5.26 mm^2$.
$$J = \frac{I}{A} = \frac{0.87 A}{5.26 × 10^{-6} m^2} = 1.65 × 10^5 A/m^2$$Explicación
La densidad de corriente en un cable conductor depende de la corriente a través del cable conductor y del área de la sección transversal del cable. Para una corriente dada, a medida que aumenta el diámetro del cable, la densidad de carga disminuye.
 Comprueba tu aprendizaje 9.4
Comprueba tu aprendizaje 9.4
¿Cuál es el significado de la densidad de corriente? La densidad de corriente es proporcional a la corriente, y la corriente es el número de cargas que pasan a través de un área de sección transversal por segundo. Las cargas se mueven a través del conductor, aceleradas por la fuerza eléctrica proporcionada por el campo eléctrico. El campo eléctrico se crea cuando se aplica una tensión a través del conductor.
En la Ley de Ohm, utilizaremos esta relación entre la densidad de corriente y el campo eléctrico para examinar la relación entre la corriente a través de un conductor y la tensión aplicada.
Antes de continuar con el próximo apartado, practica con la siguiente escena interactiva, diseñada por Julio César Domínguez Tovar, en la cual podrás apreciar y experimentar el fenómeno de conductividad eléctrica, con el fin de identificar materiales conductores y aislantes.
¿Qué impulsa la corriente? Podemos pensar en varios dispositivos, como baterías, generadores, tomas de corriente, etc., que son necesarios para mantener la corriente. Todos estos dispositivos crean una diferencia de potencial y se denominan fuentes de voltaje. Cuando una fuente de voltaje está conectada a un conductor, aplica una diferencia de potencial $V$ que crea un campo eléctrico. El campo eléctrico, a su vez, ejerce fuerza sobre las cargas libres, causando corriente. La cantidad de corriente depende no solo de la magnitud de la tensión, sino también de las características del material por el que fluye la corriente. El material puede resistir el flujo de las cargas (como los que experimentaste en la escena interactiva anterior), y la medida de cuánto resiste un material al flujo de cargas se conoce como resistividad. Esta resistividad es crudamente análoga a la fricción entre dos materiales que resiste el movimiento.
Cuando se aplica un voltaje a un conductor, se crea un campo eléctrico $\overrightarrow{\bold{E}}$, y las cargas en el conductor sienten una fuerza debida al campo eléctrico. La densidad de corriente $\overrightarrow{\bold{J}}$ que resulta depende del campo eléctrico y de las propiedades del material. Esta dependencia puede ser muy compleja. En algunos materiales, incluidos los metales a una temperatura determinada, la densidad de corriente es aproximadamente proporcional al campo eléctrico. En estos casos, la densidad de corriente se puede modelar como
$$\overrightarrow{\bold{J}} = σ\overrightarrow{\bold{E}}$$ $$σ = \frac{[J]}{[E]} = \frac{A/m^2}{V/m} = \frac{A}{V \cdot m}$$Aquí, definimos una unidad llamada ohmio con el símbolo griego mayúscula omega, $Ω$. La unidad lleva el nombre de Georg Simon Ohm, del que hablaremos más adelante en este capítulo. El $Ω$ se usa para evitar confusiones con el número $0$. Un ohmio equivale a un voltio por amperio: $1 Ω = 1 V/A$. Las unidades de conductividad eléctrica son por lo tanto $(Ω \cdot m)^{-1}$.
La conductividad es una propiedad intrínseca de un material. Otra propiedad intrínseca de un material es la resistividad o resistividad eléctrica. La resistividad de un material es una medida de la fuerza con que un material se opone al flujo de corriente eléctrica. El símbolo de resistividad es la letra griega minúscula rho, $ρ$, y la resistividad es el recíproco de la conductividad eléctrica:
$$ρ = \frac{1}{σ}$$La unidad de resistividad en unidades del SI es el ohmímetro ($Ω \cdot m$). Podemos definir la resistividad en términos del campo eléctrico y la densidad de corriente,
Cuanto mayor sea la resistividad, mayor será el campo necesario para producir una densidad de corriente dada.
Cuanto menor es la resistividad, mayor es la densidad de corriente producida por un campo eléctrico dado. Los buenos conductores tienen una alta conductividad y baja resistividad. Los buenos aislantes tienen baja conductividad y alta resistividad. La y la enumeran los valores de resistividad y conductividad para diversos materiales.
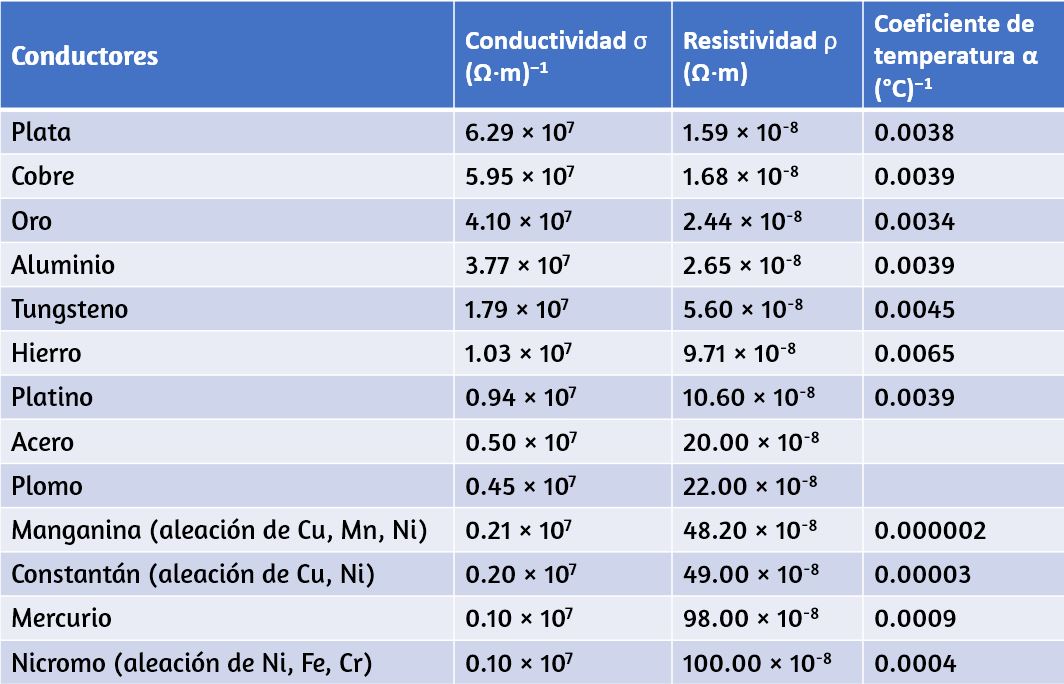
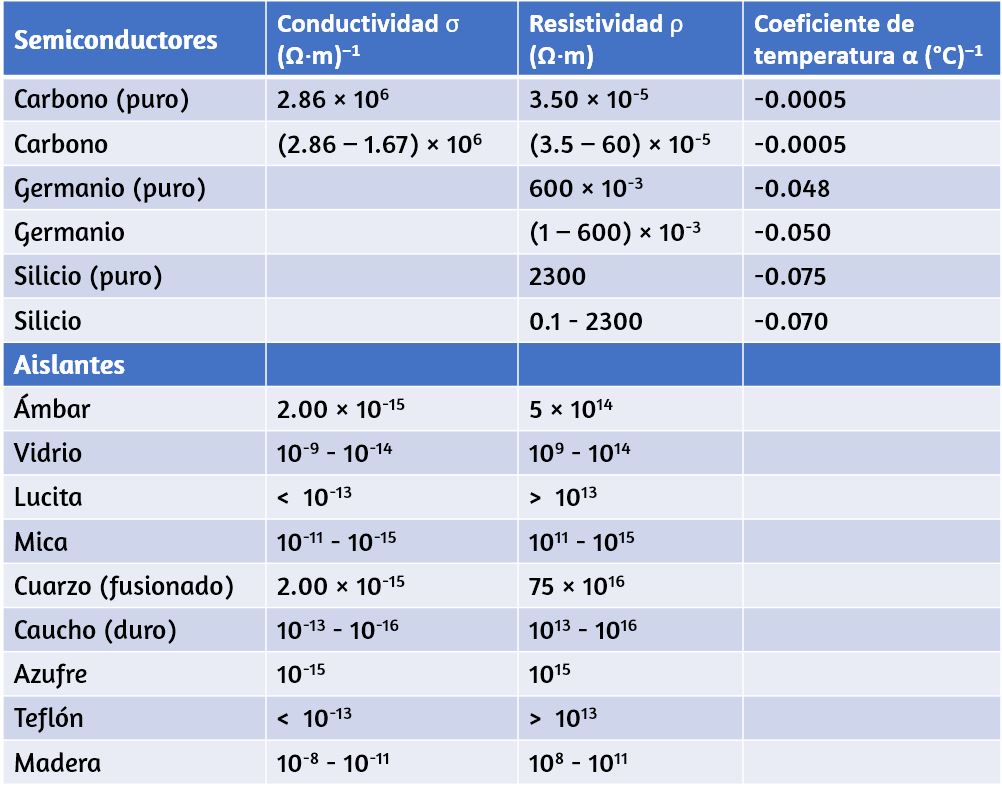
Los materiales enumerados en las tablas están separados en categorías de conductores, semiconductores y aislantes, según amplios grupos de resistividad.
Los conductores tienen la resistividad más pequeña y los aislantes tienen la mayor; los semiconductores tienen resistividad intermedia. Los conductores tienen densidades de carga diferentes pero grandes y libres, mientras que la mayoría de las cargas en los aislantes están ligadas a átomos y no se pueden mover libremente. Los semiconductores son intermedios, tienen muchas menos cargas libres que los conductores, pero tienen propiedades que hacen que el número de cargas libres dependa en gran medida del tipo y la cantidad de impurezas en el semiconductor. Estas propiedades únicas de los semiconductores se usan en la electrónica moderna, como veremos en capítulos posteriores.
Ejemplo 9.5
Densidad de corriente, resistencia y campo eléctrico para un cable que transporta corriente
Calcula la densidad de corriente, la resistencia y el campo eléctrico de un cable de cobre de $5 m$ de longitud con un diámetro de $2.053 mm$ (calibre $12$) con una corriente de $I = 10 mA$.
Estrategia
Podemos calcular la densidad de corriente encontrando primero el área de la sección transversal del cable, que es $A = 3,31 mm^2$, y la definición de densidad de corriente $J = I/A$. La resistencia se puede encontrar usando la longitud del cable $L = 5.00 m$, el área y la resistividad del cobre $ρ = 1.68 × 10^{-8} Ω \cdot m$, donde $R = ρL/A$. La resistividad y la densidad de corriente se pueden usar para encontrar el campo eléctrico.
Solución
Primero, calculamos la densidad de corriente:
$$J = \frac{I}{A} = \frac{10 × 10^{-3} A}{3.31 × 10^{-6} m^2} = 3.02 × 10^3 \frac{A}{m^2}$$La resistencia del cable es
$$R = ρ\frac{L}{A} = (1.68 × 10^{-8} Ω \cdot m)\frac{5.00 m}{3.31 × 10^{-6} m^2} = 0.025 Ω$$Finalmente, podemos encontrar el campo eléctrico:
$$E = ρJ = 1.68 × 10^{-8} Ω \cdot m \left(3.02 × 10^3 \frac{A}{m^2} \right) = 5.07 × 10^{-5} \frac{V}{m}$$Explicación
A partir de estos resultados, no es sorprendente que el cobre se use en cables para transportar corriente porque la resistencia es bastante pequeña. Ten en cuenta que la densidad de corriente y el campo eléctrico son independientes de la longitud del cable, pero el voltaje depende de la longitud.
 Comprueba tu aprendizaje 9.5
Comprueba tu aprendizaje 9.5
En la siguiente escena interactiva dse PhET Simulaciones, puedes ver cuáles son los efectos del área de la sección transversal, la longitud y la resistividad de un cable en la resistencia de un conductor. Ajusta las variables usando barras deslizantes y analiza si la resistencia se vuelve más pequeña o más grande.
Mirando hacia las y , verás una columna etiquetada como "Coeficiente de temperatura". La resistividad de algunos materiales tiene una fuerte dependencia de la temperatura.
En algunos materiales, como el cobre, la resistividad aumenta al aumentar la temperatura. De hecho, en la mayoría de los metales conductores, la resistividad aumenta al aumentar la temperatura. El aumento de la temperatura provoca un aumento de las vibraciones de los átomos en la estructura reticular de los metales, lo que impide el movimiento de los electrones. En otros materiales, como el carbono, la resistividad disminuye al aumentar la temperatura. En muchos materiales, la dependencia es aproximadamente lineal y puede modelarse usando una ecuación lineal:
donde $ρ$ es la resistividad del material a temperatura $T$, $α$ es el coeficiente de temperatura del material, y $ρ_0$ es la resistividad en $T_0$, generalmente tomada como $T_0 = 20.00 °C$.
Ten en cuenta también que el coeficiente de temperatura $α$ es negativo para los semiconductores enumerados en la , lo que significa que su resistividad disminuye al aumentar la temperatura. Se convierten en mejores conductores a mayor temperatura, ya que el aumento de la agitación térmica aumenta la cantidad de cargas libres disponibles para transportar la corriente. Esta propiedad de disminuir $ρ$ con la temperatura también está relacionada con el tipo y la cantidad de impurezas presentes en los semiconductores.
Ahora consideramos la resistencia de un cable o un componente eléctrico.
La resistencia es una medida de lo difícil que es pasar corriente a través de un cable o un componente. La resistencia depende de la resistividad. La resistividad es una característica del material utilizado para fabricar un cable u otro componente eléctrico, mientras que la resistencia es una característica del cable o componente eléctrico.
Para calcular la resistencia, considera una sección de cable conductor con área de sección transversal $A$, longitud $L$ y resistividad $ρ$. Una batería está conectada a través del conductor, proporcionando una diferencia de potencial $ΔV$ a través de él (). La diferencia de potencial produce un campo eléctrico que es proporcional a la densidad de corriente, de acuerdo con $\overrightarrow{\bold{E}} = ρ\overrightarrow{\bold{J}}$.
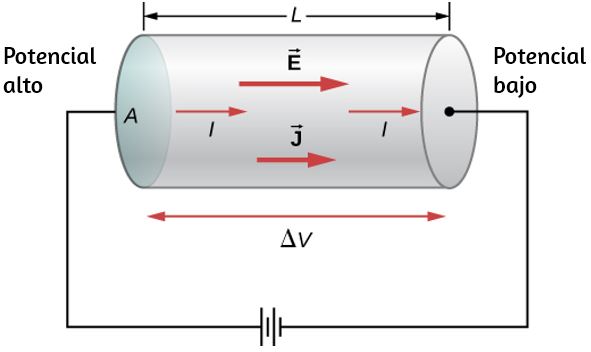
La magnitud del campo eléctrico a través del segmento del conductor es igual al voltaje dividido por la longitud, $E = V/L$, y la magnitud de la densidad de corriente es igual a la corriente dividida por el área de la sección transversal, $J = I/A$. Usando esta información y recordando que el campo eléctrico es proporcional a la resistividad y la densidad de corriente, podemos ver que el voltaje es proporcional a la corriente:
$$E = ρJ$$ $$\frac{V}{L} = ρ\frac{I}{A}$$ $$V = \left(ρ\frac{L}{A} \right)I$$Resistencia
La relación de la tensión y la corriente se define como la resistencia $R$:
$$R ≡ \frac{V}{I} \tag{9.8}$$La resistencia de un segmento cilíndrico de un conductor es igual a la resistividad del material por la longitud dividida por el área:
$$R ≡ \frac{V}{I} = ρ\frac{L}{A} \tag{9.9}$$La unidad de resistencia es el ohm u ohmio, $Ω$. Para un voltaje dado, cuanto mayor es la resistencia, menor es la corriente.
Un componente común en los circuitos electrónicos es la resistencia. La resistencia puede usarse para reducir el flujo de corriente o proporcionar una caída de voltaje. La se muestran los símbolos usados para una resistencia en diagramas esquemáticos de un circuito. El Instituto Estadounidense de Normas Nacionales (ANSI, pronunciado "AN-see") y la Comisión Electrotécnica Internacional (IEC) proporcionan dos estándares comúnmente utilizados para los diagramas de circuitos. Ambos sistemas se usan comúnmente. Utilizamos el estándar ANSI en este texto para su reconocimiento visual, pero observamos que para los circuitos más grandes y más complejos, el estándar IEC puede tener una presentación más limpia, lo que facilita la lectura.

Una resistor se puede modelar como un cilindro con un área de sección transversal $A$ y una longitud $L$, hecha de un material con una resistividad $ρ$ ().
La resistencia del resistor es $R = ρ\frac{L}{A}$.
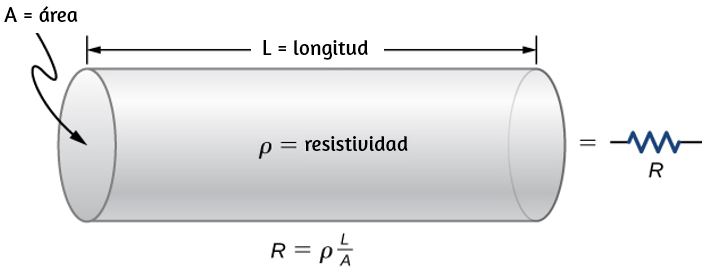
El material más común usado para hacer una resistencia es carbono. Una pista de carbono está envuelta alrededor de un núcleo de cerámica, y dos cables de cobre están conectados. Un segundo tipo de resistor es la resistencia de película metálica, que también tiene un núcleo de cerámica. La pista está hecha de un material de óxido de metal, que tiene propiedades semiconductoras similares al carbono. De nuevo, los cables de cobre se insertan en los extremos de la resistencia. La resistencia se pinta y se marca para su identificación. Una resistencia tiene cuatro bandas de colores, como se muestra en la .
En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío, calcula la resistencia según los colores del resistor y responde en el cuadro de texto. Puedes hacer todos los ejercicios que desees.
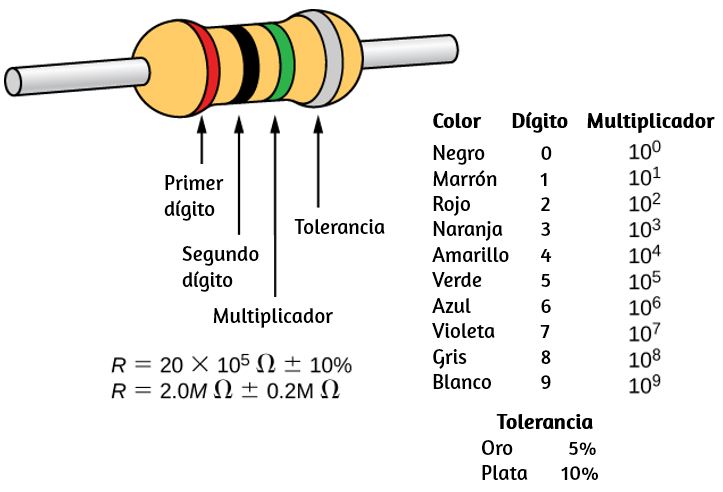
Las resistencias o resistores varían en muchos órdenes de magnitud. Algunos aislantes cerámicos, como los utilizados para soportar líneas eléctricas, tienen resistencias de $10^{12} Ω$ o más. Una persona seca puede tener una resistencia mano-a-pie de $10^5 Ω$, mientras que la resistencia del corazón humano es de aproximadamente $10^3 Ω$.
Una pieza de un metro de largo de alambre de cobre de gran diámetro puede tener una resistencia de $10^{-5} Ω$, y los superconductores no tienen resistencia en absoluto a bajas temperaturas. Como hemos visto, la resistencia está relacionada con la forma de un objeto y el material del que está compuesto.
La resistencia de un objeto también depende de la temperatura, ya que $R_0$ es directamente proporcional a $ρ$. Para un cilindro, sabemos que $R = ρ\frac{L}{A}$, por lo que si $L$ y $A$ no cambian mucho con la temperatura, $R$ tiene la misma dependencia de temperatura que $ρ$ (el examen de los coeficientes de expansión lineal muestra que son aproximadamente dos órdenes de magnitud menores que los coeficientes de temperatura típicos de resistividad, por lo que el efecto de la temperatura en $L$ y $A$ es aproximadamente dos órdenes de magnitud menor que en $ρ$). Luego
es la dependencia de la temperatura de la resistencia de un objeto, donde $R_0$ es la resistencia original (usualmente tomada a $20.00 °C$) y $R$ es la resistencia después de un cambio de temperatura $ΔT$. El código de color proporciona la resistencia de la resistencia a una temperatura de $T = 20.00 °C$.
Numerosos termómetros se basan en el efecto de la temperatura en la resistencia (). Uno de los termómetros más comunes se basa en el termistor, un cristal semiconductor con una fuerte dependencia de la temperatura, cuya resistencia se mide para obtener su temperatura. El dispositivo es pequeño, por lo que rápidamente entra en equilibrio térmico con la parte que una persona toca.
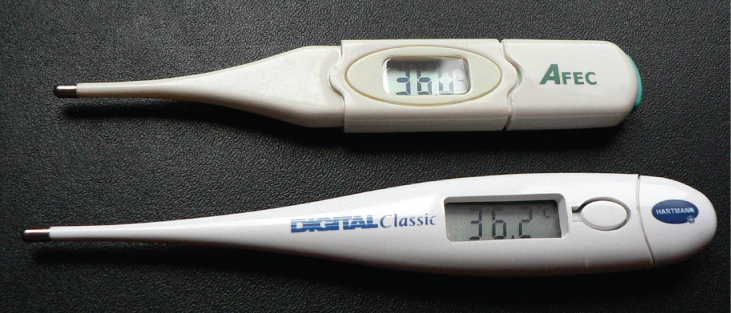
Ejemplo 9.6
Cálculo de la resistencia
Aunque se debe tener precaución al aplicar $ρ = ρ_0(1 + αΔT)$ y $R = R_0(1 + αΔT)$ para cambios de temperatura superiores a $100 °C$, para el tungsteno, las ecuaciones funcionan razonablemente bien para cambios de temperatura muy grandes. Un filamento de tungsteno a $20 °C$ tiene una resistencia de $0.350 Ω$. ¿Cuál sería la resistencia si la temperatura aumenta a $2850 °C$?
Estrategia
Esta es una aplicación directa de $R = R_0(1 + αΔT)$, ya que la resistencia original del filamento se da como $R_0 = 0.350 Ω$ y el cambio de temperatura es $ΔT = 2830 °C$.
Solución
La resistencia $R$ del filamento más caliente se obtiene al ingresar valores conocidos en la ecuación anterior:
Explicación
Observa que la resistencia cambia en más de un factor de $10$ a medida que el filamento se calienta a la temperatura alta y la corriente a través del filamento depende de la resistencia del filamento y la tensión aplicada. Si el filamento se usa en una bombilla incandescente, la corriente inicial a través del filamento, cuando la bombilla se energiza por primera vez, será mayor que la corriente una vez que el filamento alcance la temperatura de funcionamiento.
 Comprueba tu aprendizaje 9.6
Comprueba tu aprendizaje 9.6
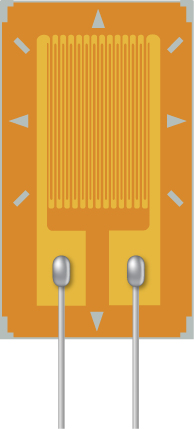
Ejemplo 9.7
La resistencia de un cable coaxial
Los cables largos a veces pueden actuar como antenas, captando el ruido electrónico, que son señales de otros equipos y dispositivos. Los cables coaxiales se usan para muchas aplicaciones que requieren que se elimine este ruido. Por ejemplo, se pueden encontrar en el hogar en conexiones de televisión por cable u otras conexiones audiovisuales. Los cables coaxiales consisten en un conductor interno de radio $r_i$ rodeado por un segundo conductor concéntrico externo con radio $r_0$ ().
El espacio entre los dos normalmente se llena con un aislante como plástico de polietileno. Se produce una pequeña cantidad de corriente de fuga radial entre los dos conductores. Determina la resistencia de un cable coaxial de longitud $L$.
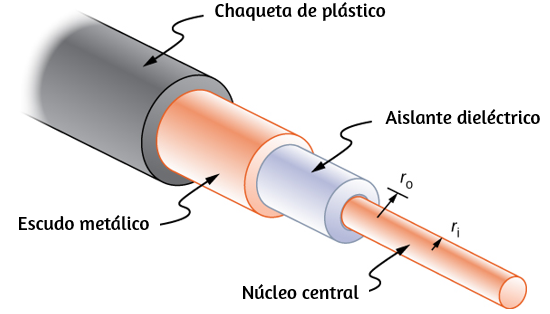
Estrategia
No podemos usar la ecuación $R = ρ\frac{L}{A}$ directamente. En cambio, observamos conchas cilíndricas concéntricas, con espesor $dr$, e integramos.
Solución
Primero encontramos una expresión para $dR$ y luego integramos de $r_i$ a $r_o$,
$$dR = \frac{ρ}{A}dr = \frac{ρ}{2πrL}dr$$ $$R = \int_{r_i}^{r_o} dR = \int_{r_i}^{{r_o}} \frac{ρ}{2πrL}dr = \frac{ρ}{2πL} \int_{r_i}^{r_o} \frac{1}{r}dr = \frac{ρ}{2πL}ln\frac{r_o}{r_i}$$Explicación
La resistencia de un cable coaxial depende de su longitud, los radios interno y externo, y la resistividad del material que separa los dos conductores.
Como esta resistencia no es infinita, se produce una pequeña fuga de corriente entre los dos conductores. Esta fuga de corriente conduce a la atenuación (o debilitamiento) de la señal que se envía a través del cable.
 Comprueba tu aprendizaje 9.7
Comprueba tu aprendizaje 9.7
Hemos estado discutiendo tres propiedades eléctricas hasta ahora en este capítulo: corriente, voltaje y resistencia. Resulta que muchos materiales muestran una relación simple entre los valores de estas propiedades, conocida como la ley de Ohm. Muchos otros materiales no muestran esta relación, por lo tanto, a pesar de llamarse la ley de Ohm, no se considera una ley de la naturaleza, como las leyes de Newton o las leyes de la termodinámica. Pero es muy útil para cálculos que involucran materiales que obedecen la ley de Ohm.
La corriente que fluye a través de la mayoría de las sustancias es directamente proporcional al voltaje V que se le aplica. El físico alemán Georg Simon Ohm (1787-1854) fue el primero en demostrar experimentalmente que la corriente en un cable de metal es directamente proporcional al voltaje aplicado:
$$I ∝ V$$Esta importante relación es la base de la ley de Ohm. Se puede ver como una relación de causa y efecto, con la causa en el voltaje y el efecto en la corriente. Esta es una ley empírica, lo que quiere decir que es un fenómeno observado experimentalmente, como la fricción. Tal relación lineal no siempre ocurre. Cualquier material, componente o dispositivo que obedezca la ley de Ohm, donde la corriente a través del dispositivo es proporcional al voltaje aplicado, se conoce como un material óhmico o componente óhmico. Cualquier material o componente que no obedezca la ley de Ohm se conoce como un material no óhmico o un componente no óhmico.
En un artículo publicado en 1827, Georg Ohm describió un experimento en el que midió el voltaje a través de corriente a través de varios circuitos eléctricos simples que contenían varias longitudes de cable. Un experimento similar se muestra en la . Este experimento se usa para observar la corriente a través de una resistencia que resulta de un voltaje aplicado. En este circuito simple, una resistencia se conecta en serie con una batería. El voltaje se mide con un voltímetro, que debe colocarse a través de la resistencia (en paralelo con la resistencia). La corriente se mide con un amperímetro, que debe estar en línea con la resistencia (en serie con la resistencia).
En esta versión actualizada del experimento original de Ohm, se realizaron varias mediciones de la corriente para varios voltajes diferentes. Cuando la batería estaba conectada como en la (a), la corriente fluía en el sentido de las agujas del reloj y las lecturas del voltímetro y el amperímetro eran positivas. ¿El comportamiento de la corriente cambia si la corriente fluye en la dirección opuesta? Para que la corriente fluya en la dirección opuesta, los cables de la batería se pueden cambiar.
Cuando se cambiaron los cables de la batería, las lecturas del voltímetro y del amperímetro fueron negativas porque la corriente fluía en la dirección opuesta, en este caso, en sentido antihorario. Los resultados de un experimento similar se muestran en la .
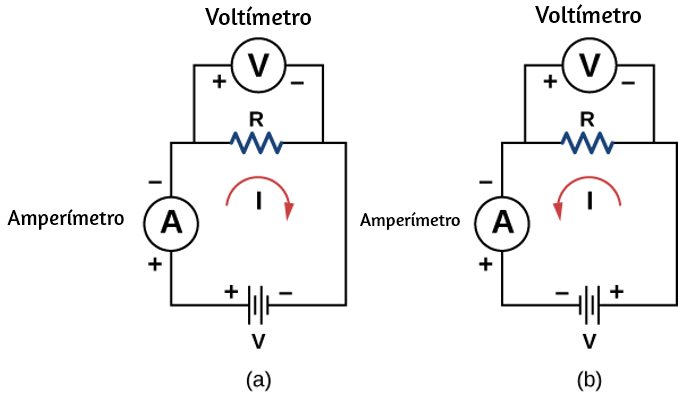
En este experimento, la tensión aplicada a través de la resistencia varía de $-10.00$ a $+10.00 V$, en incrementos de $1.00 V$. Se mide la corriente y la tensión a través de la resistencia. Se realiza una gráfica del voltaje frente a la corriente, y el resultado es aproximadamente lineal. La pendiente de la línea es la resistencia, o el voltaje dividido por la corriente. Este resultado se conoce como la ley de Ohm:
donde $V$ es la tensión medida en voltios a través del objeto en cuestión, $I$ es la corriente medida a través del objeto en amperios, y $R$ es la resistencia en unidades de ohmios. Como se indicó anteriormente, cualquier dispositivo que muestra una relación lineal entre el voltaje y la corriente se conoce como un dispositivo óhmico. Una resistencia es por lo tanto un dispositivo óhmico.
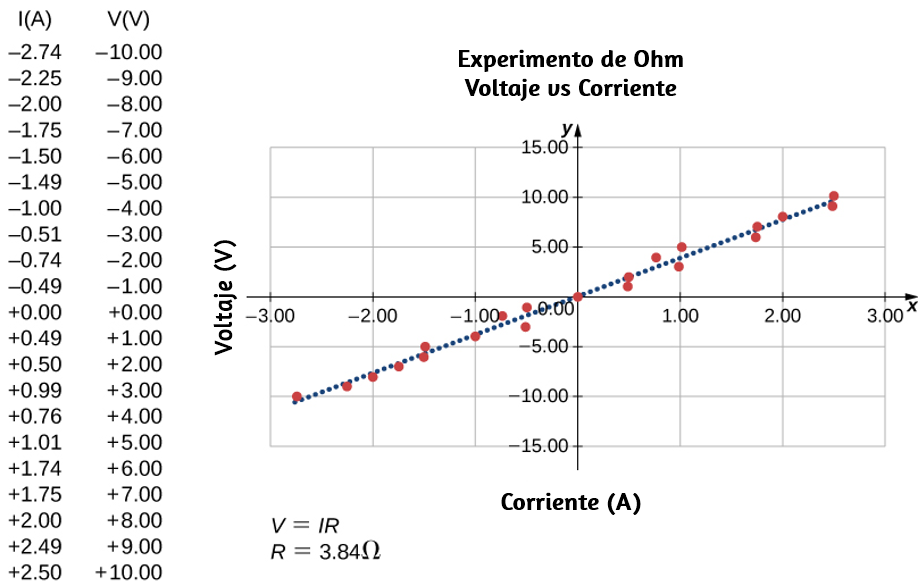
Ejemplo 9.8
Medición de la resistencia
Una resistencia de carbono a temperatura ambiente ($20 °C$) está conectada a una batería de $9.00 V$ y la corriente medida a través de la resistencia es de $3.00 mA$.
(a) ¿Cuál es el valor de la resistencia del resistor medida en ohmios?
(b) Si la temperatura de la resistencia aumenta a $60 °C$ al calentar la resistencia, ¿cuál es la corriente a través de la resistencia?
Estrategia
(a) La resistencia se puede encontrar usando la ley de Ohm. La ley de Ohm dice que $V = IR$, entonces la resistencia se puede encontrar usando $R = V/I$.
(b) En primer lugar, la resistencia depende de la temperatura, de modo que la nueva resistencia después de que se haya calentado la resistencia se puede encontrar utilizando $R = R_0(1 + αΔT)$. La corriente se puede encontrar usando la ley de Ohm en la forma $I = V/R$.
Solución
(a) El uso de la ley de Ohm y la solución para la resistencia produce el valor de la resistencia a temperatura ambiente:
$$R = \frac{V}{I} = \frac{9.00 V}{3.00 × 10^{−3} A} = 3.00 × 10^3 Ω = 3.00 kΩ$$(b) La resistencia a $60 °C$ se puede encontrar usando $R = R_0(1 + αΔT)$ donde el coeficiente de temperatura para el carbono es $α = -0,0005$. $R = R_0(1 + αΔT) = 3.00 × 10^3(1 - 0.0005(60 °C - 20 °C)) = 2.94 kΩ$.
La corriente a través de la resistencia calentada es
$$I = \frac{V}{R} = \frac{9.00 V}{2.94 × 10^3 Ω} = 3.06 × 10^{−3} A =3.06 mA$$Explicación
Un cambio en la temperatura de $40 °C$ resultó en un cambio de $2.00\%$ en la corriente. Esto puede no parecer un cambio muy grande, pero las características eléctricas cambiantes pueden tener un fuerte efecto en los circuitos. Por esta razón, muchos aparatos electrónicos, como computadoras, contienen ventiladores para eliminar el calor disipado por los componentes en los circuitos eléctricos.
 Comprueba tu aprendizaje 9.8
Comprueba tu aprendizaje 9.8
En la siguiente escena interactiva de PhET Simulaciones,observa cómo la forma de ecuación de la ley de Ohm se relaciona con un circuito simple. Ajuste el voltaje y la resistencia, y analiza el cambio de la corriente de acuerdo con la ley de Ohm. Los tamaños de los símbolos en la ecuación cambian para coincidir con el diagrama del circuito.
Los dispositivos no óhmicos no muestran una relación lineal entre el voltaje y la corriente. Uno de tales dispositivos es el elemento del circuito semiconductor conocido como diodo. Un diodo es un dispositivo de un circuito que permite el flujo de corriente en una sola dirección. En la se muestra un diagrama de un circuito simple que consta de una batería, un diodo y una resistencia. Aunque no cubrimos la teoría del diodo en esta sección, el diodo puede probarse para ver si es un dispositivo óhmico o no óhmico.
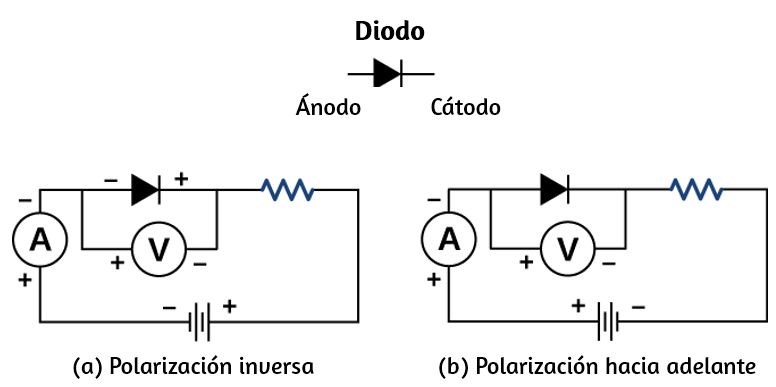
En la se muestra un gráfico de corriente frente a voltaje. Ten en cuenta que el comportamiento del diodo se muestra como la corriente frente a la tensión, mientras que la operación de la resistencia se muestra como el voltaje frente a la corriente. Un diodo consiste en un ánodo y un cátodo. Cuando el ánodo tiene un potencial negativo y el cátodo tiene un potencial positivo, como se muestra en la parte (a), se dice que el diodo tiene polarización inversa. Con polarización inversa, el diodo tiene una resistencia extremadamente grande y hay muy poco flujo de corriente, esencialmente cero, a través del diodo y la resistencia.
A medida que aumenta la tensión aplicada al circuito, la corriente permanece esencialmente cero, hasta que el voltaje alcanza la tensión de ruptura y el diodo conduce la corriente, como se muestra en la .
Cuando la batería y el potencial a través del diodo están invertidos, haciendo que el ánodo sea positivo y el cátodo negativo, el diodo conduce y la corriente fluye a través del diodo si el voltaje es mayor a $0.7 V$. La resistencia del diodo es cercana a cero (Esta es la razón de la resistencia en el circuito, si no estuviera allí, la corriente sería muy grande). Puedes ver en el gráfico de la que el voltaje y la corriente no tienen una relación lineal. Por lo tanto, el diodo es un ejemplo de un dispositivo no óhmico.
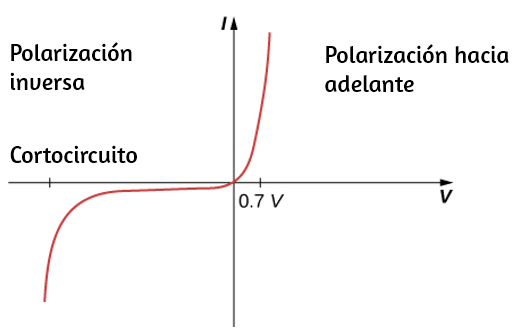
La ley de Ohm se establece comúnmente como $V = IR$, pero originalmente se declaró como una vista microscópica, en términos de la densidad de corriente, la conductividad y el campo eléctrico.
Esta vista microscópica sugiere que la proporcionalidad $V ∝ I$ proviene de la velocidad de deriva de los electrones libres en el metal que resulta de un campo eléctrico aplicado. Como se dijo anteriormente, la densidad de corriente es proporcional al campo eléctrico aplicado. La reformulación de la ley de Ohm se le atribuye a Gustav Kirchhoff, cuyo nombre veremos nuevamente en el próximo capítulo.
Terminamos este apartado con una escena interactiva, diseñada por Julio César Domínguez Tovar en el Proyecto Telesecundaria, que permite identificar la relación que existe entre la resistencia eléctrica, con algunas características de los materiales.
En un circuito eléctrico, la energía eléctrica se convierte continuamente en otras formas de energía. Por ejemplo, cuando una corriente fluye en un conductor, la energía eléctrica se convierte en energía térmica dentro del conductor. El campo eléctrico, suministrado por la fuente de voltaje, acelera los electrones libres, aumentando su energía cinética por un corto tiempo. Esta energía cinética aumentada se convierte en energía térmica a través de colisiones con los iones de la estructura reticular del conductor. Previamente definimos la potencia como la velocidad a la que el trabajo se realiza mediante una fuerza medida en vatios. La potencia también se puede definir como la velocidad a la que se transfiere la energía. En esta sección, discutimos la tasa de tiempo de transferencia de energía, o potencia, en un circuito eléctrico.
La energía está asociada por muchas personas con la electricidad. Las líneas de transmisión de energía pueden venir a la mente. También pensamos en las bombillas en términos de potencia nominal en vatios. ¿Cuál es la expresión de la energía eléctrica?
Comparemos una bombilla de $25 W$ con una bombilla de $60 W$ ( (a)). La bombilla de $60 W$ brilla más que la bombilla de $25 W$. Aunque no se muestra, una bombilla de $60 W$ también es más cálida que la bombilla de $25 W$. El calor y la luz se producen por la conversión de energía eléctrica. La energía cinética perdida por los electrones en las colisiones se convierte en la energía interna del conductor y la radiación. ¿Cómo se relacionan el voltaje, la corriente y la resistencia con la energía eléctrica?

Para calcular la potencia eléctrica, considera una diferencia de voltaje existente a través de un material (). El potencial eléctrico $V_1$ es más alto que el potencial eléctrico en $V_2$, y la diferencia de voltaje es negativa $V = V_2 - V_1$. Existe un campo eléctrico entre los dos potenciales, que apunta desde el potencial más alto al potencial más bajo. Recuerda que el potencial eléctrico se define como la energía potencial por carga, $V = ΔU/q$, y la carga $ΔQ$ pierde la energía potencial que se mueve a través de la diferencia de potencial.
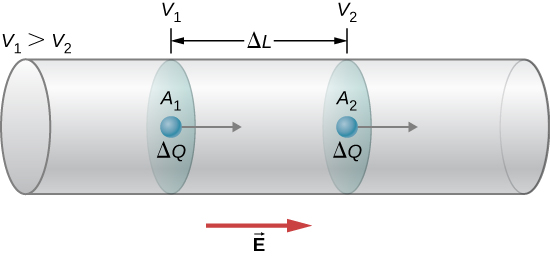
Si la carga es positiva, la carga experimenta una fuerza debida al campo eléctrico $\overrightarrow{\bold{F}} = m\overrightarrow{\bold{a}} = ΔQ\overrightarrow{\bold{E}}$. Esta fuerza es necesaria para mantener la carga en movimiento. Esta fuerza no actúa para acelerar la carga a lo largo de toda la distancia $ΔL$ debido a las interacciones de la carga con los átomos y los electrones libres en el material. La velocidad, y por lo tanto la energía cinética, de la carga no aumentan durante todo el recorrido a través de $ΔL$, y la carga que pasa a través del área $A_2$ tiene la misma velocidad de deriva $v_d$ que la carga que pasa por el área $A_1$. Sin embargo, se trabaja en la carga, por el campo eléctrico, que cambia la energía potencial. Dado que el cambio en la diferencia de potencial eléctrico es negativo, se encuentra que el campo eléctrico es
$$E = -\frac{(V_2 - V_1)}{ΔL} = \frac{V}{ΔL}$$El trabajo realizado en la carga es igual a la fuerza eléctrica multiplicada por la longitud a la que se aplica la fuerza,
$$W = FΔL = (ΔQE)ΔL = \left(\frac{ΔQ}{ΔL} \right)ΔL = ΔQV = ΔU$$La carga se mueve a una velocidad de deriva $v_d$ por lo que el trabajo realizado en la carga da como resultado una pérdida de energía potencial, pero la energía cinética promedio permanece constante. La energía potencial eléctrica perdida aparece como energía térmica en el material. En una escala microscópica, la transferencia de energía se debe a las colisiones entre la carga y las moléculas del material, lo que conduce a un aumento de la temperatura en el material. La pérdida de energía potencial da como resultado un aumento en la temperatura del material, que se disipa como radiación. En una resistencia, se disipa como calor y, en una bombilla, se disipa como calor y luz.
La potencia disipada por el material como calor y luz es igual a la tasa de cambio de tiempo del trabajo:
$$P = \frac{ΔU}{Δt} = -\frac{ΔQV}{Δt} = IV$$Con una resistencia, la caída de voltaje en la resistencia se disipa en forma de calor. La ley de Ohm establece que el voltaje en la resistencia es igual a la corriente multiplicada por la resistencia, $V = IR$. La potencia disipada por la resistencia es por lo tanto
$$P = IV = I(IR) = I^2R o P = IV = \left(\frac{V}{R} \right)V = \frac{V^2}{R}$$Si una resistencia está conectada a una batería, la potencia se disipa como energía radiante por los cables y la resistencia es igual a $P = IV = I^2R = V^2/R$. La potencia suministrada por la batería es igual a la corriente multiplicada por el voltaje, $P = IV$.
Potencia electrica
La potencia eléctrica ganada o perdida por cualquier dispositivo tiene la forma
$$P = IV \tag{9.12}$$La potencia disipada por una resistencia tiene la forma
$$P = I^2R = \frac{V^2}{R} \tag{9.13}$$Se pueden obtener diferentes puntos de vista de las tres expresiones diferentes para la energía eléctrica. Por ejemplo, $P = V^2/R$ implica que cuanto menor sea la resistencia conectada a una fuente de tensión dada, mayor será la potencia entregada. Además, dado que la tensión se cuadra en $P = V^2/R$, el efecto de aplicar una tensión más alta es tal vez mayor de lo esperado. Por lo tanto, cuando el voltaje se duplica a una bombilla de $25 W$, su potencia casi se cuadruplica a aproximadamente $100 W$, y se consume. Si la resistencia del foco permanece constante, su potencia sería exactamente de $100 W$, pero a mayor temperatura, su resistencia también es mayor.
Ejemplo 9.9
Cálculo de potencia en dispositivos eléctricos
Un motor de malacate de $CC$ tiene una potencia nominal de $20.00 A$ con una tensión de $115 V$. Cuando el motor funciona a su potencia máxima, puede levantar un objeto con un peso de $4900.00 N$ una distancia de $10.00 m$, en $30.00 s$, a una velocidad constante. (a) ¿Cuál es la potencia consumida por el motor? (b) ¿Cuál es la potencia utilizada para levantar el objeto? Ignora la resistencia del aire. (c) Suponiendo que la diferencia en la potencia consumida por el motor y la potencia utilizada para levantar el objeto se disipa en forma de calor por la resistencia del motor, ¿estima la resistencia del motor?
Estrategia
(a) La potencia consumida por el motor se puede encontrar usando $P = IV$.
(b) La potencia utilizada para levantar el objeto a una velocidad constante se puede encontrar usando $P = Fv$, donde la velocidad es la distancia dividida por el tiempo.
La fuerza hacia arriba suministrada por el motor es igual al peso del objeto porque la aceleración es constante.
(c) La resistencia del motor se puede encontrar usando $P = I^2R$.
Solución
(a) La potencia consumida por el motor es igual a $P = IV$ y la corriente se da como $20.00 A$ y el voltaje es $115.00 V$:
$$P = IV = (20.00 A)115.00 V = 2300.00 W$$(b) La potencia utilizada para levantar el objeto es igual a $P = Fv$ donde la fuerza es igual al peso del objeto ($1960 N$) y la magnitud de la velocidad es $v = \frac{10.00 m}{30.00 s} = 0.33 m/s$,
$$P = Fv = (4900 N)0,33 m/s = 1633,33 W$$(c) La diferencia en la potencia es igual a $2300.00 W - 1633.33 W = 666.67 W$ y la resistencia se puede encontrar usando $P = I^2R$:
$$R = \frac{P}{I^2} = \frac{666.67 W}{(20.00 A)^2} = 1.67 Ω$$Explicación
La resistencia del motor es bastante pequeña. La resistencia del motor se debe a muchos devanados de alambre de cobre. La potencia disipada por el motor puede ser significativa ya que la potencia térmica disipada por el motor es proporcional al cuadrado de la corriente ($P = I^2R$).
 Comprueba tu aprendizaje 9.9
Comprueba tu aprendizaje 9.9
Un fusible () es un dispositivo que protege un circuito de corrientes que son demasiado altas. Un fusible es básicamente un trozo corto de alambre entre dos contactos. Como hemos visto, cuando una corriente se está ejecutando a través de un conductor, la energía cinética de los portadores de carga se convierte en energía térmica en el conductor. La pieza de alambre en el fusible está bajo tensión y tiene un punto de fusión bajo. El cable está diseñado para calentarse y romperse a la corriente nominal. El fusible se destruye y debe ser reemplazado, pero protege el resto del circuito. Los fusibles actúan rápidamente, pero hay un pequeño retraso mientras el cable se calienta y se rompe.

Cuantos más electrodomésticos usas y cuanto más tiempo permanezcan encendidos, mayor será tu factura de electricidad.
Este hecho familiar se basa en la relación entre energía y potencia. Pagas por la energía utilizada. Desde $P = \frac{dE}{dt}$, vemos que
$$E = \int Pdt$$es la energía utilizada por un dispositivo que usa energía $P$ durante un intervalo de tiempo $t$. Si la potencia se entrega a una tasa constante, entonces la energía puede ser hallada por $E = Pt$. Por ejemplo, cuantas más bombillas ardían, mayor era el $P$ utilizado; cuanto más tiempo llevan, mayor es $t$.
La unidad de energía en las facturas eléctricas es el kilovatio-hora $(kW \cdot h)$, consistente con la relación $E = Pt$. Es fácil estimar el costo de operar aparatos eléctricos si tienes alguna idea de tu tasa de consumo de energía en vatios o kilovatios, el tiempo que llevan en horas y el costo por kilovatio-hora para tu servicio eléctrico. El kilovatio-hora, como todas las demás unidades de energía especializadas, como las calorías de los alimentos, se pueden convertir en julios. Puedes demostrar que $1kW \cdot h = 3.6 × 10^6 J$.
La energía eléctrica ($E$) utilizada puede reducirse reduciendo el tiempo de uso o reduciendo el consumo de energía de ese artefacto. Esto no solo reduce el costo, sino que también reduce el impacto sobre el medio ambiente. Las mejoras en la iluminación son algunas de las formas más rápidas de reducir la energía eléctrica utilizada en un hogar o un negocio. Aproximadamente el $20$% del uso de energía de una casa se destina a la iluminación, y el número de establecimientos comerciales se acerca al $40$%.
Las luces fluorescentes son aproximadamente cuatro veces más eficientes que las incandescentes; esto es cierto tanto para los tubos largos como para las luces fluorescentes compactas (CFL) (consulta la (b)).
Por lo tanto, una bombilla incandescente de $60 W$ puede reemplazarse por una CFL de $15 W$, que tiene el mismo brillo y color. Las lámparas fluorescentes compactas tienen un tubo doblado dentro de un globo o un tubo en forma de espiral, todas conectadas a una base atornillable estándar que se ajusta a las tomas de luz incandescentes estándar (los problemas originales con el color, el parpadeo, la forma y la alta inversión inicial para las lámparas fluorescentes compactas se han abordado en los últimos años).
La transferencia de calor de estas lámparas fluorescentes compactas es menor, y duran hasta 10 veces más que las bombillas incandescentes. La importancia de una inversión en tales bulbos se aborda en el siguiente ejemplo. Las nuevas luces LED blancas (que son grupos de pequeñas bombillas LED) son incluso más eficientes (el doble que las lámparas fluorescentes compactas) y duran cinco veces más que las lámparas fluorescentes compactas.
Ejemplo 9.10
Cálculo de la rentabilidad de la bombilla LED
El reemplazo típico de una bombilla incandescente de $100 W$ es una bombilla LED de $20 W$. La bombilla LED de $20 W$ puede proporcionar la misma cantidad de luz que la bombilla incandescente de $100 W$. ¿Cuál es el ahorro en el costo de usar la bombilla LED en lugar de la bombilla incandescente durante un año, suponiendo que $\$0.10$ por kilovatio-hora es la tasa de energía promedio cobrada por la compañía eléctrica? Supongamos que la bombilla está encendida durante tres horas al día.
Estrategia
(a) Calcula la energía utilizada durante el año para cada foco, usando $E = Pt$.
(b) Multiplica la energía por el costo.
Solución
(a) Calcula la potencia de cada bombilla.
(b) Calcula el costo de cada uno.
$$\textsf{Costo}_{\textsf{Incandescente}} = 109.5 kW-h \left(\frac{\$0.10}{kW \cdot h} \right) = \$10.95$$ $$\textsf{Costo}_{\textsf{Led}} = 21.90 kW-h \left(\frac{\$0.10}{kW \cdot h} \right) = \$2.19$$Explicación
Una bombilla LED usa un $80$% menos de energía que la bombilla incandescente, ahorrando $\$8.76$ sobre la bombilla incandescente por un año. La bombilla LED puede costar $\$20.00$ y la bombilla incandescente de $100 W$ puede costar $\$0.75$, que se debe usar en el cálculo. Una vida útil típica de una bombilla incandescente es de $1200$ horas y de $50,000$ horas para la bombilla LED. La bombilla incandescente duraría $1,08$ años a las $3$ horas por día y la bombilla LED duraría $45,66$ años.
El costo inicial de la bombilla LED es alto, pero el costo para el propietario será de $\$0.69$ para las bombillas incandescentes frente a $\$0.44$ para las bombillas LED por año (tenga en cuenta que las bombillas LED bajan de precio). El ahorro de costos por año es de aproximadamente $\$8.50$, y eso es solo por una bombilla.
 Comprueba tu aprendizaje 9.10
Comprueba tu aprendizaje 9.10
Cambiar las bombillas incandescentes a bombillas CFL o LED es una forma sencilla de reducir el consumo de energía en los hogares y los sitios comerciales. Las bombillas CFL funcionan con un mecanismo muy diferente al de las luces incandescentes. El mecanismo es complejo y está fuera del alcance de este capítulo, pero aquí hay una descripción muy general del mecanismo. Las bombillas CFL contienen argón y vapor de mercurio dentro de un tubo en forma de espiral. Las bombillas CFL usan un "balasto" que aumenta el voltaje utilizado por la bombilla CFL. El balasto produce una corriente eléctrica que pasa a través de la mezcla de gases y excita las moléculas de gas. Las moléculas de gas excitadas producen luz ultravioleta (UV), que a su vez estimula el recubrimiento fluorescente en el interior del tubo. Esta capa fluoresce en el espectro visible, emitiendo luz visible.
Los tubos fluorescentes tradicionales y las bombillas CFL tenían un pequeño retraso de hasta unos pocos segundos mientras la mezcla se "calentaba" y las moléculas alcanzaban un estado de excitación. Cabe señalar que estas bombillas contienen mercurio, que es venenoso, pero si la bombilla se rompe, el mercurio nunca se libera. Incluso si la bombilla está rota, el mercurio tiende a permanecer en la capa fluorescente.
La cantidad también es bastante pequeña y la ventaja del ahorro de energía puede superar la desventaja de usar mercurio.
Las bombillas CFL están siendo reemplazadas por bombillas LED, donde LED significa "diodo emisor de luz". El diodo se discutió brevemente como un dispositivo no ómico, hecho de material semiconductor, que esencialmente permite el flujo de corriente en una dirección. Los LED son un tipo especial de diodo hecho de materiales semiconductores infundidos con impurezas en combinaciones y concentraciones que permiten que la energía extra del movimiento de los electrones durante la excitación eléctrica se convierta en luz visible. Los dispositivos semiconductores se explicarán con mayor detalle en Física de la Materia Condensada.
Los LED comerciales se están convirtiendo rápidamente en el estándar para la iluminación comercial y residencial, en sustitución de las bombillas incandescentes y CFL. Están diseñados para el espectro visible y están construidos con galio dopado con átomos de arsénico y fósforo. El color emitido por un LED depende de los materiales utilizados en el semiconductor y la corriente. En los primeros años del desarrollo del LED, los LED pequeños que se encontraban en las placas de circuitos eran de color rojo, verde y amarillo, pero las bombillas LED ahora se pueden programar para producir millones de colores de luz y diferentes tonos de luz blanca.
El ahorro de energía puede ser significativo al reemplazar una bombilla incandescente o una bombilla CFL con una luz LED. Las bombillas se clasifican por la cantidad de energía que consume la bombilla, y la cantidad de salida de luz se mide en lúmenes. El lumen ($lm$) es la unidad de flujo luminoso derivada del SI y es una medida de la cantidad total de luz visible emitida por una fuente.
Una bombilla incandescente de $60 W$ se puede reemplazar con una bombilla CFL de $13$ a $15 W$ o una bombilla LED de $6$ a $8 W$, las tres tienen una salida de luz de aproximadamente $800 lm$. Una tabla de salida de luz para algunas bombillas de uso común aparece en la .
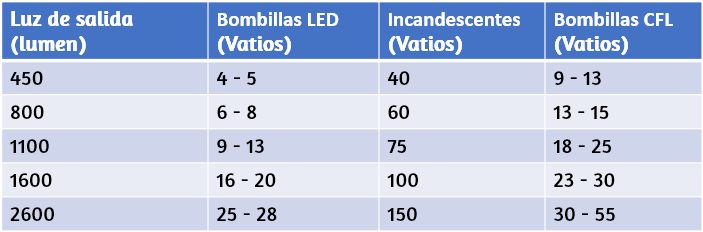
La duración de la vida de los tres tipos de bombillas es significativamente diferente. Una bombilla LED tiene una vida útil de $50,000$ horas, mientras que la CFL tiene una vida útil de $8,000$ horas y la incandescente dura solo $1200$ horas. La bombilla LED es el tratamiento más resistente y duradero que se puede resistir fácilmente, como sacudidas y golpes. La bombilla incandescente tiene poca tolerancia al mismo tratamiento ya que el filamento y el vidrio pueden romperse fácilmente.
La bombilla CFL también es menos duradera que la bombilla LED debido a su construcción de vidrio. La cantidad de calor emitido es $3.4 btu/h$ para la bombilla LED de $8 W$, $85 btu/h$ para la bombilla incandescente de $60 W$ y $30 btu/h$ para la bombilla CFL. Como se mencionó anteriormente, una desventaja principal de la bombilla CFL es que contiene mercurio, una neurotoxina, y debe desecharse como un desecho peligroso. A partir de estos datos, es fácil entender por qué la bombilla LED se está convirtiendo rápidamente en el estándar en iluminación.
En este capítulo, hemos discutido las relaciones entre voltajes, corriente, resistencia y potencia. La muestra un resumen de las relaciones entre estas cantidades medibles para dispositivos óhmicos (Recuerda que los dispositivos óhmicos siguen la ley de Ohm $V = IR$). Por ejemplo, si necesitas calcular la potencia, usa la sección rosa, que muestra que $P = VI$, $P = V^2/R$ y $P = I^2R$.
La ecuación que uses depende de los valores que te den o midas. Por ejemplo, si te dan la corriente y la resistencia, usa $P = I^2R$. Aunque todas las combinaciones posibles pueden parecer abrumadoras, no olvides que todas son combinaciones de solo dos ecuaciones, la ley de Ohm ($V = IR$) y la potencia ($P = IV$).
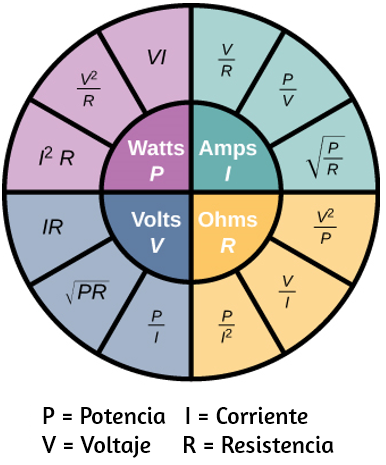
Toca la fuente de alimentación de tu computadora portátil u otro dispositivo. Probablemente se siente un poco cálido. Ese calor es un subproducto no deseado del proceso de conversión de energía eléctrica doméstica en una corriente que puede usar tu dispositivo. Aunque la energía eléctrica es razonablemente eficiente, otras pérdidas están asociadas a ella. La transmisión de energía eléctrica produce pérdidas de línea $I^2R$.
Estas pérdidas de línea existen ya sea que la energía se genere a partir de centrales eléctricas convencionales (que usan carbón, petróleo o gas), plantas nucleares, plantas solares, plantas hidroeléctricas o parques eólicos. Estas pérdidas se pueden reducir, pero no eliminar, al transmitir utilizando un voltaje más alto. Sería maravilloso si estas pérdidas de línea pudieran eliminarse, pero eso requeriría líneas de transmisión que tengan resistencia cero. En un mundo que tiene un interés global en no desperdiciar energía, la reducción o eliminación de esta energía térmica no deseada sería un logro significativo, ¿es posible?
En 1911, Heike Kamerlingh Onnes de la Universidad de Leiden, un físico holandés, observaba la dependencia de la temperatura de la resistencia del elemento mercurio. Él enfrió la muestra de mercurio y notó el comportamiento familiar de una dependencia lineal de la resistencia a la temperatura; a medida que la temperatura disminuía, la resistencia disminuía. Kamerlingh Onnes continuó enfriando la muestra de mercurio, utilizando helio líquido. Cuando la temperatura se acercó a los $4,2 K$ ($-269,2 °C$), la resistencia se redujo bruscamente a cero (). Esta temperatura se conoce como la temperatura crítica $T_c$ para el mercurio. La muestra de mercurio entró en una fase donde la resistencia era absolutamente cero.
Este fenómeno se conoce como superconductividad (Nota: si conectan los cables de un ohmímetro de tres dígitos a través de un conductor, la lectura comúnmente se muestra como $0.00 Ω$. La resistencia del conductor no es realmente cero, es menor de $0.01 Ω$). Hay varios métodos para medir resistencias muy pequeñas, como el método de cuatro puntos, pero un ohmímetro no es un método aceptable para probar la resistencia en la superconductividad.
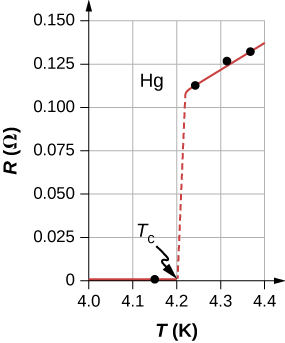
A medida que continuaba la investigación, se descubrió que otros materiales entraban en una fase superconductora, cuando la temperatura alcanzaba casi el cero absoluto. En 1941, se encontró una aleación de nitruro de niobio que podría convertirse en superconductora a $T_c = 16K$ ($-257 °C$) y en 1953, se encontró que el silicio de vanadio se volvió superconductor a $T_c = 17,5 K$ $(-255,7 °C)$. Las temperaturas para la transición a la superconductividad fueron aumentando lentamente. Extrañamente, muchos materiales que hacen buenos conductores, como cobre, plata y oro, no exhiben superconductividad.
Imagina el ahorro de energía si las líneas de transmisión para las estaciones generadoras de energía eléctrica pudieran ser superconductoras a temperaturas cercanas a la temperatura ambiente. Una resistencia de cero ohmios significa que no hay pérdidas de $I^2R$ y un gran impulso para reducir el consumo de energía. El problema es que $T_c = 17.5K$ todavía está muy frío y en el rango de temperaturas de helio líquido. A esta temperatura, no es rentable transmitir energía eléctrica debido a los requisitos de enfriamiento.
Se observó un gran salto en 1986, cuando un equipo de investigadores, dirigido por el Dr. Ching Wu Chu de la Universidad de Houston, fabricó un compuesto cerámico frágil con una temperatura de transición de $T_c = 92K$ ($-181 °C$). El material cerámico, compuesto por óxido de itrio, bario y cobre ($YBCO$), era un aislante a temperatura ambiente. Aunque esta temperatura todavía parece bastante fría, está cerca del punto de ebullición del nitrógeno líquido, un líquido comúnmente utilizado en refrigeración. Es posible que hayas notado camiones refrigerados que viajan por la carretera etiquetados como "refrigerado por nitrógeno líquido".
la cerámica $YBCO$ es un material que podría ser útil para transmitir energía eléctrica porque el ahorro de costos de la reducción de las pérdidas de $I^2R$ es mayor que el costo de enfriar el cable superconductor, por lo que es económicamente viable. Hubo y hay muchos problemas de ingeniería que superar. Por ejemplo, a diferencia de los cables eléctricos tradicionales, que son flexibles y tienen una resistencia a la tracción decente, las cerámicas son frágiles y se romperían en lugar de estirarse bajo presión. Los procesos que son bastante simples con los cables tradicionales, como hacer conexiones, se vuelven difíciles cuando se trabaja con cerámica. Los problemas son difíciles y complejos, y los científicos e ingenieros de materiales están ideando soluciones innovadoras.
Una consecuencia interesante de la resistencia que tiende a cero es que una vez que se establece una corriente en un superconductor, persiste sin una fuente de voltaje aplicada. Se han configurado los bucles de corriente en un superconductor y se ha observado que los ciclos de corriente persisten durante años sin descomponerse.
La resistencia cero no es el único fenómeno interesante que ocurre cuando los materiales alcanzan sus temperaturas de transición. Un segundo efecto es la exclusión de campos magnéticos. Esto se conoce como el efecto Meissner (). Un imán ligero y permanente colocado sobre una muestra superconductora levitará en una posición estable sobre el superconductor. Se han desarrollado trenes de alta velocidad que levitan sobre fuertes imanes superconductores, eliminando la fricción que normalmente se experimenta entre el tren y las vías. En Japón, la línea de prueba de Yamanashi Maglev se abrió el 3 de abril de 1997. En abril de 2015, el vehículo de prueba MLX01 alcanzó una velocidad de $374 mph$ ($603 km/h$).

Las tablas y muestra una lista de selección de elementos, compuestos y superconductores de alta temperatura, junto con las temperaturas críticas para las cuales se vuelven superconductores. Cada sección está clasificada desde la temperatura crítica más alta hasta la más baja. También se enumera el campo magnético crítico para algunos de los materiales. Esta es la fuerza del campo magnético que destruye la superconductividad. Finalmente, se enumera el tipo del superconductor.
Hay dos tipos de superconductores. Hay 30 metales puros que muestran resistividad cero por debajo de su temperatura crítica y exhiben el efecto Meissner, la propiedad de excluir campos magnéticos del interior del superconductor mientras que el superconductor está a una temperatura inferior a la temperatura crítica. Estos metales se llaman superconductores tipo I. La superconductividad existe solo por debajo de sus temperaturas críticas y por debajo de una intensidad de campo magnético crítico. Los superconductores tipo I están bien descritos por la teoría BCS (que se describe a continuación). Los superconductores tipo I tienen aplicaciones prácticas limitadas debido a que la fuerza del campo magnético crítico necesario para destruir la superconductividad es bastante baja.
Se ha descubierto que los superconductores de tipo II tienen campos magnéticos críticos mucho más altos y, por lo tanto, pueden transportar densidades de corriente mucho más altas mientras permanecen en el estado superconductor. Una colección de varias cerámicas que contienen óxido de cobre-bario tienen temperaturas críticas mucho más altas para la transición a un estado superconductor. Los materiales superconductores que pertenecen a esta subcategoría de los superconductores tipo II a menudo se clasifican como superconductores de alta temperatura.
Los superconductores de tipo I, junto con algunos superconductores de tipo II, se pueden modelar utilizando la teoría BCS, propuesta por John Bardeen, Leon Cooper y Robert Schrieffer. Aunque la teoría está más allá del alcance de este capítulo, aquí se brinda un breve resumen de la teoría (Se proporcionan más detalles en Física de la Materia Condensada). La teoría considera pares de electrones y cómo se acoplan entre sí a través de interacciones retículo-vibración. A través de las interacciones con la red cristalina, los electrones cercanos al nivel de energía de Fermi sienten una pequeña fuerza de atracción y forman pares (pares de Cooper), y el acoplamiento se conoce como una interacción de fonones. Los electrones individuales son fermiones, que son partículas que obedecen el principio de exclusión de Pauli. El principio de exclusión de Pauli en mecánica cuántica establece que dos fermiones idénticos (partículas con giro de medio entero) no pueden ocupar el mismo estado cuántico simultáneamente. Cada electrón tiene cuatro números cuánticos $(n, l, m_l, m_s)$. El número cuántico principal ($n$) describe la energía del electrón, el número cuántico del momento angular orbital ($l$) indica la distancia más probable desde el núcleo, el número cuántico magnético ($m_l$) describe los niveles de energía en la subescala y el electrón el número cuántico de espín ($m_s$) describe la orientación del giro del electrón, ya sea hacia arriba o hacia abajo.
A medida que el material entra en un estado superconductor, los pares de electrones actúan más como bosones, que pueden condensarse en el mismo nivel de energía y no necesitan obedecer el principio de exclusión de Pauli. Los pares de electrones tienen una energía ligeramente menor y dejan un espacio de energía por encima de ellos del orden de $0.001 eV$. Esta brecha de energía inhibe las interacciones de colisión que conducen a la resistividad ordinaria. Cuando el material está por debajo de la temperatura crítica, la energía térmica es menor que la banda prohibida y el material muestra cero resistividad.
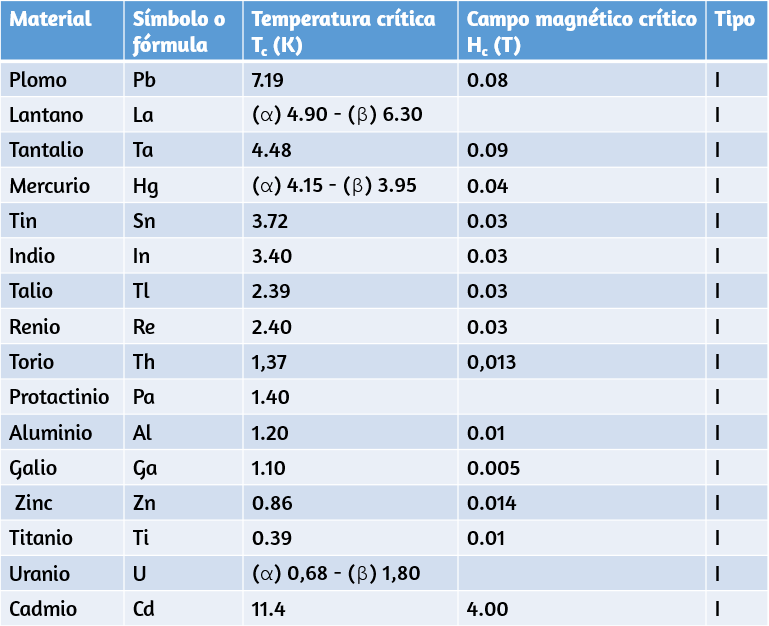
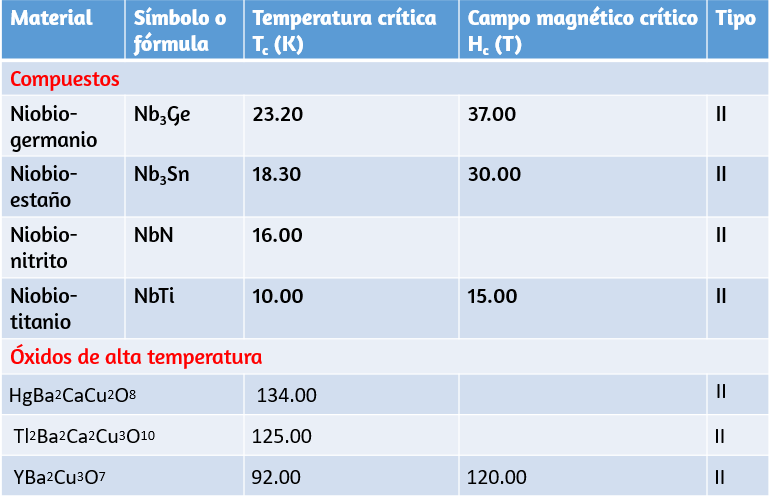
Los superconductores se pueden usar para hacer imanes superconductores. Estos imanes son 10 veces más fuertes que los electroimanes más fuertes. Estos imanes se utilizan actualmente en imágenes de resonancia magnética (MRI), que produce imágenes de alta calidad del interior del cuerpo sin radiación peligrosa.
Otra aplicación interesante de la superconductividad es el SQUID (dispositivo de interferencia cuántica superconductor). Un SQUID es un magnetómetro muy sensible utilizado para medir campos magnéticos extremadamente sutiles. El funcionamiento del SQUID se basa en bucles superconductores que contienen uniones Josephson. Una unión de Josephson es el resultado de una predicción teórica hecha por B. D. Josephson en un artículo publicado en 1962.
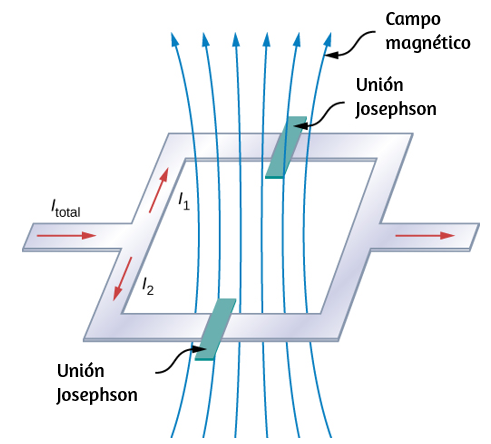
En el artículo, Josephson describió cómo una supercorriente puede fluir entre dos piezas de superconductor separadas por una capa delgada de aislante. Este fenómeno ahora se llama efecto Josephson. El SQUID consiste en un circuito de corriente superconductora que contiene dos uniones Josephson, como se muestra en la . Cuando el bucle se coloca incluso en un campo magnético muy débil, hay un efecto de interferencia que depende de la intensidad del campo magnético.
La superconductividad es un fenómeno fascinante y útil. A temperaturas críticas cerca del punto de ebullición del nitrógeno líquido, la superconductividad tiene aplicaciones especiales en resonancias magnéticas, aceleradores de partículas y trenes de alta velocidad. ¿Llegaremos a un estado en el que podamos hacer que los materiales entren en la fase superconductora a temperaturas cercanas a la temperatura ambiente? Parece muy lejano, pero si a los científicos en 1911 se les preguntara si alcanzaríamos temperaturas de nitrógeno líquido con una cerámica, podrían haber pensado que no era plausible.
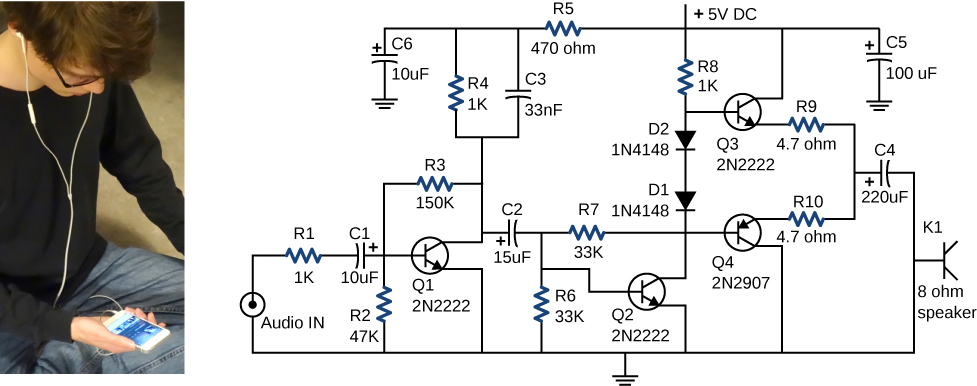
En los capítulos anteriores, hablamos de componentes eléctricos, incluidos condensadores, resistencias y diodos. En este capítulo, usamos estos componentes eléctricos en circuitos. Un circuito es una colección de componentes eléctricos conectados para realizar una tarea específica. La muestra un circuito amplificador, que toma una señal de amplitud pequeña y la amplifica para alimentar los altavoces en auriculares. Aunque el circuito parece complejo, en realidad consiste en un conjunto de circuitos en serie, paralelo y serie paralelo.
La segunda sección de este capítulo cubre el análisis de circuitos en serie y en paralelo que consisten en resistencias. Más adelante en este capítulo, presentamos las ecuaciones y técnicas básicas para analizar cualquier circuito, incluidos aquellos que no son reducibles mediante la simplificación de elementos paralelos y en serie. Pero primero, debemos entender cómo alimentar un circuito.
Si olvida apagar las luces de su automóvil, se atenúan lentamente a medida que se agota la batería. ¿Por qué no parpadean de repente cuando la energía de la batería se ha ido? Su atenuación gradual implica que el voltaje de salida de la batería disminuye a medida que se agota la batería. La razón de la disminución del voltaje de salida para las baterías agotadas es que todas las fuentes de voltaje tienen dos partes fundamentales: una fuente de energía eléctrica y una resistencia interna. En esta sección, examinamos la fuente de energía y la resistencia interna.
El voltaje tiene muchas fuentes, algunas de las cuales se muestran en la . Todos estos dispositivos crean una diferencia de potencial y pueden suministrar corriente si están conectados a un circuito. Un tipo especial de diferencia de potencial se conoce como fuerza electromotriz (fem). La fem no es una fuerza en absoluto, pero el término "fuerza electromotriz" se usa por razones históricas. Fue acuñado por Alessandro Volta en el siglo XIX, cuando inventó la primera batería, también conocida como pila voltaica. Debido a que la fuerza electromotriz no es una fuerza, es común referirse a estas fuentes simplemente como fuentes de fem, en lugar de fuentes de fuerza electromotriz.

Si la fuerza electromotriz no es una fuerza, ¿qué es la fem y qué es una fuente de fem? Para responder a estas preguntas, considera un circuito simple de una lámpara de $12 V$ conectada a una batería de $12 V$, como se muestra en la . La batería se puede modelar como un dispositivo de dos terminales que mantiene un terminal a un potencial eléctrico más alto que el segundo terminal. El mayor potencial eléctrico a veces se denomina terminal positiva y está etiquetado con un signo más. El terminal de menor potencial a veces se denomina terminal negativa y se etiqueta con un signo menos. Esta es la fuente de la fem.
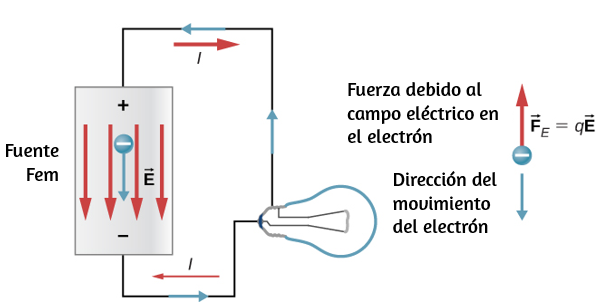
Cuando la fuente de fem no está conectada a la lámpara, no hay un flujo neto de carga dentro de la fuente de fem. Una vez que la batería está conectada a la lámpara, las cargas fluyen desde un terminal de la batería, a través de la lámpara (haciendo que la lámpara se encienda) y de vuelta a la otra terminal de la batería.
Si consideramos el flujo de corriente positivo (convencional), las cargas positivas salen del terminal positivo, viajan a través de la lámpara y entran al terminal negativo. El flujo de corriente positivo es útil para la mayoría del análisis de circuitos en este capítulo, pero en alambres metálicos y resistencias, los electrones contribuyen más a la corriente, fluyendo en la dirección opuesta al flujo de corriente positiva. Por lo tanto, es más realista considerar el movimiento de electrones para el análisis del circuito en la . Los electrones salen del terminal negativo, viajan a través de la lámpara y regresan al terminal positivo. Para que la fuente de fem pueda mantener la diferencia de potencial entre los dos terminales, las cargas negativas (electrones) deben moverse del terminal positivo al terminal negativo.
La fuente de fem actúa como una bomba de carga, moviendo cargas negativas del terminal positivo al terminal negativo para mantener la diferencia de potencial. Esto aumenta la energía potencial de las cargas y, por lo tanto, el potencial eléctrico de las cargas.
La fuerza en la carga negativa del campo eléctrico está en la dirección opuesta al campo eléctrico, como se muestra en la . Para que las cargas negativas se muevan al terminal negativo, se debe trabajar con las cargas negativas. Esto requiere energía, que proviene de las reacciones químicas en la batería. El potencial se mantiene alto en el terminal positivo y bajo en el terminal negativo para mantener la diferencia de potencial entre los dos terminales. La fem es igual al trabajo realizado en la carga por unidad de carga $(ε = dW/dq)$ cuando no fluye la corriente. Como la unidad de trabajo es el joule y la unidad de carga es el culombio, la unidad de fem es el voltio ($1 V = 1 J/C$).
El voltaje de terminal $V_{\textsf{terminal}}$ de una batería es el voltaje medido a través de los terminales de la batería cuando no hay carga conectada al terminal. Una batería ideal es una fuente de fem que mantiene un voltaje de terminal constante, independientemente de la corriente entre los dos terminales.
Una batería ideal no tiene resistencia interna, y la tensión del terminal es igual a la fem de la batería. En la siguiente sección, mostraremos que una batería real tiene resistencia interna y la tensión del terminal es siempre menor que la fem de la batería.
La combinación de sustancias químicas y la composición de los terminales en una batería determinan su fem. La batería de ácido de plomo utilizada en automóviles y otros vehículos es una de las combinaciones más comunes de productos químicos. La muestra una sola celda (una de seis) de esta batería.
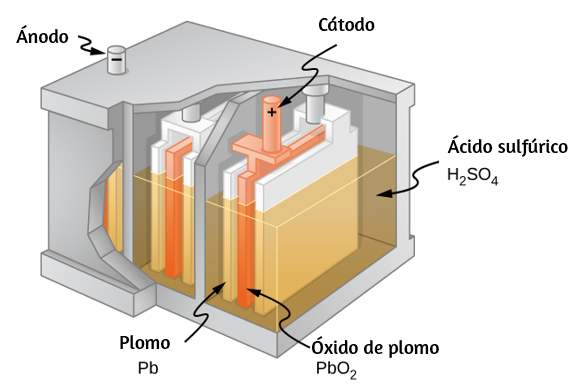
El terminal del cátodo (positivo) de la celda está conectado a una placa de óxido de plomo, mientras que el terminal del ánodo (negativo) está conectado a una placa de plomo. Ambas placas están sumergidas en ácido sulfúrico, el electrolito para el sistema.
Conocer un poco acerca de cómo interactúan los químicos en una batería de plomo ayuda a entender el potencial creado por la batería. La muestra el resultado de una sola reacción química. Dos electrones se colocan en el ánodo, lo que lo hace negativo, siempre que el cátodo suministre dos electrones. Esto deja el cátodo cargado positivamente, porque ha perdido dos electrones. En resumen, una separación de carga ha sido impulsada por una reacción química.
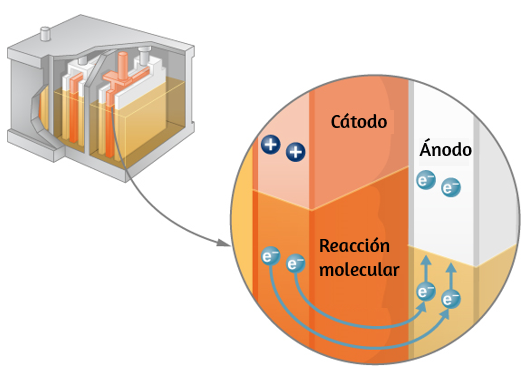
Ten en cuenta que la reacción no tiene lugar a menos que haya un circuito completo para permitir que se suministren dos electrones al cátodo. En muchas circunstancias, estos electrones provienen del ánodo, fluyen a través de una resistencia y regresan al cátodo. Ten en cuenta también que dado que las reacciones químicas implican sustancias con resistencia, no es posible crear la fem sin una resistencia interna.
La cantidad de resistencia al flujo de corriente dentro de la fuente de voltaje se llama resistencia interna. La resistencia interna r de una batería puede comportarse de maneras complejas. En general, aumenta a medida que se agota una batería, debido a la oxidación de las placas o la reducción de la acidez del electrolito. Sin embargo, la resistencia interna también puede depender de la magnitud y la dirección de la corriente a través de una fuente de tensión, su temperatura e incluso su historia. La resistencia interna de las células recargables de níquel-cadmio, por ejemplo, depende de cuántas veces y cuán profundamente se hayan agotado. Un modelo simple para una batería consiste en una fuente de fem idealizada $ε$ y una resistencia interna $r$ ().

Supongamos que una resistencia externa, conocida como la resistencia de carga $R$, está conectada a una fuente de voltaje como una batería, como en la . La figura muestra un modelo de una batería con una fem, una resistencia interna $r$, y una resistencia de carga $R$ conectada a través de sus terminales. Con el uso del flujo de corriente convencional, las cargas positivas salen del terminal positivo de la batería, viajan a través de la resistencia y vuelven al terminal negativo de la batería.
La tensión del terminal de la batería depende de la fem, la resistencia interna y la corriente, y es igual a
Para una fem dada y una resistencia interna, la tensión del terminal disminuye a medida que la corriente aumenta debido a la caída potencial $Ir$ de la resistencia interna.
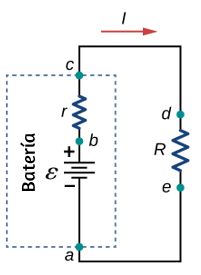
Un gráfico de la diferencia de potencial entre cada elemento del circuito se muestra en la . Una corriente I recorre el circuito y la caída potencial a través de la resistencia interna es igual a $Ir$. La tensión del terminal es igual a $ε - Ir$, que es igual a la caída de potencial a través de la resistencia de carga $IR = ε - Ir$. Al igual que con la energía potencial, es el cambio en el voltaje lo que es importante. Cuando se usa el término "voltaje", suponemos que en realidad es el cambio en el potencial, o $ΔV$. Sin embargo, $Δ$ a menudo se omite por conveniencia.
La corriente a través de la resistencia de carga es $I = εr + R$. Vemos en esta expresión que cuanto menor es la resistencia interna $r$, mayor es la corriente que la fuente de tensión suministra a su carga $R$. A medida que las baterías se agotan, $r$ aumenta. Si $r$ se convierte en una fracción significativa de la resistencia de carga, entonces la corriente se reduce significativamente, como lo ilustra el siguiente ejemplo.
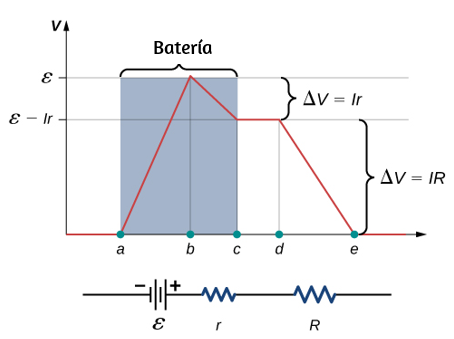
Ejemplo 10.1
Analizando un circuito con una batería y una carga
Una batería determinada tiene una fem de $12.00 V$ y una resistencia interna de $0.100 Ω$. (a) Calcula su voltaje de terminal cuando está conectado a una carga de $10.00 Ω$. (b) ¿Cuál es el voltaje del terminal cuando está conectado a una carga de $0.500 Ω$? (c) ¿Qué potencia se disipa la carga de $0.500 Ω$?
(d) Si la resistencia interna aumenta a $0.500 Ω$, encuentra la corriente, el voltaje del terminal y la potencia disipada por una carga de $0.500 Ω.$
Estrategia
El análisis anterior dio una expresión de la corriente cuando se tiene en cuenta la resistencia interna. Una vez que se encuentra la corriente, la tensión del terminal puede calcularse usando la ecuación $V_{\textsf{terminal}} = ε - Ir$. Una vez que se encuentra la corriente, también podemos encontrar la potencia disipada por la resistencia.
Solución
(a) Al ingresar los valores dados para la fem, la resistencia a la carga y la resistencia interna en la expresión anterior, se obtiene
$$I = \frac{ε}{R + r} = \frac{12.00 V}{10.10 Ω} = 1.188 A$$Ingresa los valores conocidos en la ecuación $V_{\textsf{terminal}} = ε - Ir$ para obtener la tensión del terminal:
$$V_{\textsf{terminal}} = ε - Ir = 12.00 V - (1.188 A)(0.100 Ω) = 11.90 V.$$La tensión del terminal aquí es solo ligeramente menor que la fem, lo que implica que la corriente consumida por esta carga ligera no es significativa.
(b) Del mismo modo, con $R_{\textsf{carga}} = 0.500 Ω$, la corriente es
$$I = \frac{ε}{R + r} = \frac{12.00 V}{0.600 Ω} = 20.00 A$$La tensión del terminal es ahora:
$$V_{\textsf{terminal}} = ε - Ir = 12.00 V - (20.00 A)(0.100 Ω) = 10.00 V.$$La tensión del terminal muestra una reducción más significativa en comparación con la fem, lo que implica $0.500 Ω$ es una carga pesada para esta batería. Una "carga pesada" significa un mayor consumo de corriente de la fuente pero no una resistencia mayor.
(c) La potencia disipada por la carga de $0.500 Ω$ se puede encontrar con la fórmula $P = I^2R$. Ingresando los valores conocidos obtenemos:
$$P = I^2R = (20.0 A)^2(0.500 Ω) = 2.00 × 10^2 W.$$Observa que esta potencia también puede obtenerse utilizando la expresión $V^2R$ o $IV$, donde $V$ es la tensión del terminal ($10,0 V$ en este caso).
(d) Aquí, la resistencia interna se ha incrementado, tal vez debido al agotamiento de la batería, hasta el punto en que es tan grande como la resistencia a la carga. Como antes, primero encontramos la corriente al ingresar los valores conocidos en la expresión, produciendo $$I = \frac{ε}{R + r} = \frac{12.00 V}{1.00 Ω} = 12.00 A$$
Ahora el voltaje del terminal es
$$V_{\textsf{terminal}} = ε - Ir = 12.00 V - (12.00 A)(0.500 Ω) = 6.00 V,$$y la potencia disipada por la carga es
$$P = I^2R = (12.00 A)^2(0.500 Ω) = 72.00 W.$$Vemos que la resistencia interna aumentada ha disminuido significativamente el voltaje, la corriente y la potencia del terminal entregados a una carga.
Explicación
La resistencia interna de una batería puede aumentar por muchas razones. Por ejemplo, la resistencia interna de una batería recargable aumenta a medida que aumenta la cantidad de veces que se recarga la batería. El aumento de la resistencia interna puede tener dos efectos en la batería. Primero, la tensión del terminal disminuirá. En segundo lugar, la batería puede sobrecalentarse debido a la mayor potencia disipada por la resistencia interna.
 Comprueba tu aprendizaje 10.1
Comprueba tu aprendizaje 10.1
Los probadores de batería, como los de la , usan pequeños resistores de carga para extraer intencionalmente corriente para determinar si el potencial del terminal cae por debajo de un nivel aceptable. Aunque es difícil medir la resistencia interna de una batería, los comprobadores de batería pueden proporcionar una medición de la resistencia interna de la batería. Si la resistencia interna es alta, la batería está débil, como lo demuestra su bajo voltaje de terminal.

Algunas baterías se pueden recargar pasando una corriente a través de ellas en la dirección opuesta a la corriente que suministran a un dispositivo. Esto se hace rutinariamente en automóviles y baterías para pequeños aparatos eléctricos y dispositivos electrónicos (). La salida de voltaje del cargador de la batería debe ser mayor que la fem de la batería para revertir la corriente a través de él.
Esto hace que el voltaje del terminal de la batería sea mayor que la fem, ya que $V = ε - Ir$ e $I$ ahora es negativo.

Es importante entender las consecuencias de la resistencia interna de las fuentes de fem, como las baterías y las células solares, pero a menudo, el análisis de los circuitos se realiza con el voltaje de la batería de la terminal, como lo hemos hecho en las secciones anteriores. El voltaje del terminal se conoce simplemente como $V$, eliminando el "terminal" del subíndice. Esto se debe a que la resistencia interna de la batería es difícil de medir directamente y puede cambiar con el tiempo.
hemos descrito el término 'resistencia' y explicamos el diseño básico de un resistor. Básicamente, un resistor limita el flujo de carga en un circuito y es un dispositivo óhmico donde $V = IR$. La mayoría de los circuitos tienen más de un resistor. Si varios resistores están conectados entre sí y conectados a una batería, la corriente suministrada por la batería depende de la resistencia equivalente del circuito.
La resistencia equivalente de una combinación de resistores depende de sus valores individuales y de cómo están conectados. Las combinaciones más simples de resistores son conexiones en serie y en paralelo (). En un circuito en serie, la corriente de salida del primer resistor fluye a la entrada del segundo; por lo tanto, la corriente es la misma en cada resistor. En un circuito paralelo, todos los cables de un resistor de un lado de los resistores están conectados entre sí y todos los cables del otro lado están conectados entre sí. En el caso de una configuración paralela, cada resistor tiene la misma caída de potencial a través de él, y las corrientes a través de cada resistor pueden ser diferentes, dependiendo del resistor. La suma de las corrientes individuales es igual a la corriente que fluye a las conexiones paralelas.
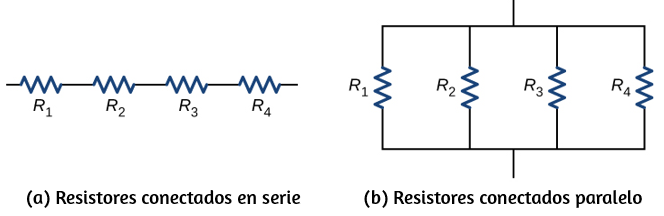
Se dice que los resistores están en serie siempre que la corriente fluya a través de los resistores secuencialmente. Considera la , que muestra tres resistores en serie con un voltaje aplicado igual a $V_{ab}$. Como solo hay una ruta para que fluyan las cargas, la corriente es la misma a través de cada resistor. El resistencia equivalente de un conjunto de resistores en una conexión en serie es igual a la suma algebraica de las resistencias individuales.

En la , la corriente procedente de la fuente de tensión fluye a través de cada resistor, por lo que la corriente a través de cada resistor es la misma. La corriente a través del circuito depende de la tensión suministrada por la fuente de tensión y la resistencia de los resistores. Para cada resistor, ocurre una caída potencial que es igual a la pérdida de energía potencial eléctrica a medida que una corriente viaja a través de cada resistor. Según la ley de Ohm, la caída de potencial $V$ a través de un resistor cuando una corriente fluye a través de él se calcula usando la ecuación $V = IR$, donde $I$ es la corriente en amperios ($A$) y $R$ es la resistencia en ohmios ($Ω$). Dado que la energía se conserva y el voltaje es igual a la energía potencial por carga, la suma de la tensión aplicada al circuito por la fuente y el potencial cae a través de los resistores individuales alrededor de un circuito debe ser igual a cero:
$$\sum_{i = 1}^{N} V_i = 0$$Esta ecuación se conoce a menudo como la ley de bucle de Kirchhoff, que veremos con más detalle más adelante en este capítulo. Para la , la suma de la caída potencial de cada resistor y la tensión suministrada por la fuente de tensión debe ser igual a cero:
$$\begin{split} V − V_1 − V_2 − V_3 &= 0 \\ V &= V_1 + V_2 + V_3 \\ &= IR_1 + IR_2 + IR_3 \\ I &= \frac{V}{R_1 + R_2 + R_3} = \frac{V}{R_{\textsf{eq}}} \end{split}$$Dado que la corriente a través de cada componente es la misma, la igualdad se puede simplificar a una resistencia equivalente, que es solo la suma de las resistencias de los resistores individuales.
Se puede conectar cualquier cantidad de resistores en serie. Si $N$ resistores están conectados en serie, la resistencia equivalente es
Un resultado de los componentes conectados en un circuito en serie es que si algo le sucede a un componente, afecta a todos los otros componentes. Por ejemplo, si varias lámparas están conectadas en serie y una bombilla se quema, todas las otras lámparas se apagan.
Ejemplo 10.2
Resistencia, corriente y potencia equivalentes en un circuito de serie
Una batería con una tensión de terminal de $9 V$ está conectada a un circuito que consta de cuatro resistores de $20 Ω$ y una de $10 Ω$ en serie (). Supongamos que la batería tiene una resistencia interna insignificante. (a) Calcula la resistencia equivalente del circuito. (b) Calcula la corriente a través de cada resistencia. (c) Calcula la caída potencial a través de cada resistencia. (d) Determina la potencia total disipada por los resistores y la potencia suministrada por la batería.
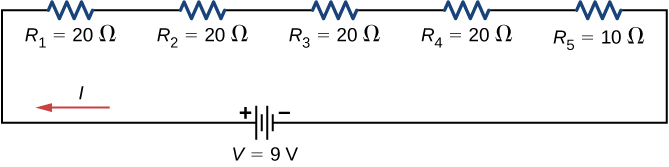
Estrategia
En un circuito en serie, la resistencia equivalente es la suma algebraica de las resistencias. La corriente a través del circuito se puede encontrar a partir de la ley de Ohm y es igual al voltaje dividido por la resistencia equivalente. La caída potencial a través de cada resistor se puede encontrar usando la ley de Ohm. La potencia disipada por cada resistor se puede encontrar usando $P = I^2R$, y la potencia total disipada por los resistores es igual a la suma de la potencia disipada por cada resistor. La potencia suministrada por la batería se puede encontrar usando $P = Iε$.
Solución
(a) La resistencia equivalente es la suma algebraica de las resistencias:
(B) La corriente a través del circuito es la misma para cada resistor en un circuito en serie y es igual al voltaje aplicado dividido por la resistencia equivalente:
$$I = \frac{V}{R_{\textsf{eq}}} = \frac{9 V}{90 Ω} = 0.1 A$$(c) La caída potencial a través de cada resistor se puede encontrar usando la ley de Ohm:
$$V_1 = V_2 = V_3 = V_4 = (0.1 A)20 Ω = 2 V$$ $$V_5 = (0.1 A)10 Ω = 1 V$$ $$V_1 + V_2 + V_3 + V_4 + V_5 = 9 V$$Ten en cuenta que la suma de las caídas de potencial en cada resistor es igual a la tensión suministrada por la batería.
(d) La potencia disipada por un resistor es igual a $P = I^2R$, y la potencia suministrada por la batería es igual a $P = Iε$
$$P_1 = P_2 = P_3 = P_4 = (0.1 A)^2(20 Ω) = 0.2 W$$ $$P_5 = (0.1 A)^2(10 Ω) = 0.1 W$$ $$P_{\textsf{disipada}} = 0.2 W + 0.2 W + 0.2 W + 0.2 W + 0.1 W = 0.9 W$$ $$P_{\textsf{fuente}} = Iε = (0.1 A)(9 V) = 0.9 W$$Explicación
Hay varias razones por las que usaríamos resistores múltiples en lugar de un solo resistor con una resistencia igual a la resistencia equivalente del circuito. Quizás un resistor del tamaño requerido no está disponible, o tenemos que disipar el calor generado, o queremos minimizar el costo de los resistores. Cada resistor puede costar unos pocos centavos a unos pocos dólares, pero cuando se multiplica por miles de unidades, el ahorro de costos puede ser apreciable.
 Comprueba tu aprendizaje 10.2
Comprueba tu aprendizaje 10.2
Resumiremos brevemente las principales características de los resistores en serie:
1. Los resistores en serie se suman para obtener la resistencia equivalente:
$$R_{\textsf{eq}} = R_1 + R_2 + R_3 + ... + R_{N-1} + R_N = \sum_{i = 1}^{N} R_i$$2. La misma corriente fluye a través de cada resistor en serie.
3. Los resistores individuales en serie no obtienen el voltaje total de la fuente, sino que lo dividen. La caída de potencial total en una configuración de resistores en serie es igual a la suma de las caídas de potencial en cada resistor.
La muestra resistores en paralelo, conectados a una fuente de voltaje. Los resistores están en paralelo cuando un extremo de todos los resistores están conectados por un cable continuo de resistencia insignificante y el otro extremo de todas los resistores también están conectados entre sí a través de un cable continuo de resistencia despreciable. La caída de potencial a través de cada resistor es la misma. La corriente a través de cada resistor se puede encontrar usando la ley de Ohm $I = V/R$, donde el voltaje es constante a través de cada resistor. Por ejemplo, los faros, la radio y otros sistemas de un automóvil están conectados en paralelo, de modo que cada subsistema utiliza el voltaje completo de la fuente y puede operar de manera completamente independiente. Lo mismo es cierto para el cableado en tu casa o cualquier edificio.
La corriente que fluye desde la fuente de voltaje en la depende del voltaje suministrado por la fuente de voltaje y la resistencia equivalente del circuito. En este caso, la corriente fluye desde la fuente de tensión y entra en una unión, o nodo, donde el circuito se divide a través de las resistencias $R_1$ y $R_2$. A medida que las cargas fluyen desde la batería, algunas pasan a través del resistor $R_1$ y otras fluyen a través del resistor $R_2$. La suma de las corrientes que fluyen en una unión debe ser igual a la suma de las corrientes que salen de la unión:
$$\sum I_{\textsf{entrada}} = \sum I_{\textsf{salida}}$$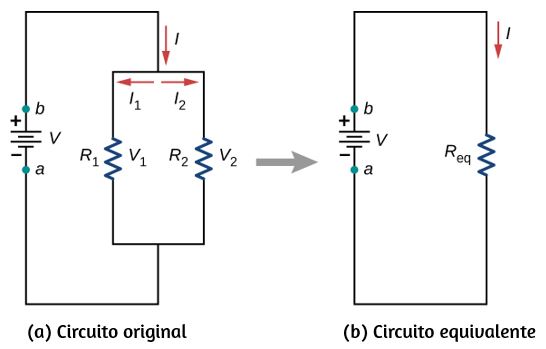
Esta ecuación se conoce como la regla de unión de Kirchhoff y se analizará en la siguiente sección. En la , la regla da $I = I_1 + I_2$. Hay dos bucles en este circuito, lo que conduce a las ecuaciones $V = I_1R_1$ e $I_1R_1 = I_2R_2$. Observa que el voltaje entre los resistores en paralelo es el mismo ($V = V_1 = V_2$) y la corriente es aditiva:
$$I = I_1 + I_2 = \frac{V_1}{R_1} + \frac{V_2}{R_2} = \frac{V}{R_1} + \frac{V}{R_2} = V \left(\frac{1}{R_1} + \frac{1}{R_2} \right) = \frac{V}{R_{\textsf{eq}}}$$ $$R_{\textsf{eq}} = \left(\frac{1}{R_1} + \frac{1}{R_2} \right)^{-1}$$Generalizando a cualquier cantidad de $N$ resistores, la resistencia equivalente $R_{\textsf{eq}}$ de una conexión en paralelo está relacionada con los resistores individuales por
Esta relación da como resultado una $R_{\textsf{eq}}$ que es menor que la más pequeña de las resistencias individuales. Cuando los resistores se conectan en paralelo, fluye más corriente de la fuente que la que fluiría para cualquiera de ellos individualmente, por lo que la resistencia total es menor.
Ejemplo 10.3
Análisis de un circuito en paralelo
Tres resistores $R_1 = 1.00 Ω$, $R_2 = 2.00 Ω$ y $R_3 = 2.00 Ω$, están conectados en paralelo. La conexión en paralelo está conectada a una fuente de voltaje $V = 3.00 V$. (a) ¿Cuál es la resistencia equivalente? (b) Encuentra la corriente suministrada por la fuente al circuito en paralelo. (c) Calcula las corrientes en cada resistor y demuestra que éstas se suman para igualar la salida de la corriente de la fuente. (d) Calcula la potencia disipada por cada resistor. (e) Encuentra la potencia de salida de la fuente y demuestra que es igual a la potencia total disipada por los resistores.
Estrategia
(a) La resistencia total para una combinación paralela de resistencias se encuentra
utilizando $\displaystyle R_{\textsf{eq}} = \left(\sum_{i = 1}^{N} \frac{1}{R_i} \right)^{-1}$
Ten en cuenta que en estos cálculos, cada respuesta intermedia se muestra con un dígito adicional.
(b) La corriente suministrada por la fuente se puede encontrar a partir de la ley de Ohm, sustituyendo $R_{\textsf{eq}}$ por la resistencia total $I = \frac{V}{R_{\textsf{eq}}}$.
(c) Las corrientes individuales se calculan fácilmente a partir de la ley de Ohm $(I_i = \frac{V_i}{R_i})$, ya que cada resistor obtiene el voltaje completo. La corriente total es la suma de las corrientes individuales:
$$I = \sum_{i = 1}^{N} I_i$$(d) La potencia disipada por cada resistor se puede encontrar usando cualquiera de las ecuaciones relacionadas con la potencia a la corriente, el voltaje y la resistencia, ya que los tres son conocidos. Usemos $P_i = V^2/R_i$, ya que cada resistor obtiene voltaje completo.
(e) La potencia total también se puede calcular de varias maneras, usa $P = IV$.
Solución
(a) La resistencia total para una combinación paralela de resistores se encuentra utilizando la ecuación 10.3. Al ingresar valores conocidos, obtenemos:
La resistencia total con el número correcto de dígitos significativos es $R_{\textsf{eq}} = 0.50 Ω$. Como se predijo, $R_{\textsf{eq}}$ es menor que la resistencia individual más pequeña.
(b) La corriente total se puede encontrar a partir de la ley de Ohm, sustituyendo $R_{\textsf{eq}}$ por la resistencia total. Esto da
$$I = \frac{V}{R_{\textsf{eq}}} = \frac{3.00 V}{0.50 Ω} = 6.00 A$$La corriente $I$ para cada dispositivo es mucho más grande que para los mismos dispositivos conectados en serie (ver el ejemplo anterior). Un circuito con conexiones en paralelo tiene una resistencia total menor que las resistencias conectadas en serie.
(c) Las corrientes individuales se calculan fácilmente a partir de la ley de Ohm, ya que cada resistor obtiene el voltaje completo. Así,
$$I_1 = \frac{V}{R_1} = \frac{3.00 V}{1.00 Ω} = 3.00 A$$similarmente:
$$I_2 = \frac{V}{R_2} = \frac{3.00 V}{2.00 Ω} = 1.50 A$$ $$I_3 = \frac{V}{R_3} = \frac{6.00 V}{2.00 Ω} = 3.00 A$$La corriente total es la suma de las corrientes individuales:
$$I_1 + I_2 + I_3 = 6.00 A.$$(d) La potencia disipada por cada resistor se puede encontrar usando cualquiera de las ecuaciones que relacionan la potencia con la corriente, el voltaje y la resistencia, ya que los tres son conocidos. Usemos $P = V^2/R$, ya que cada resistor obtiene voltaje completo. Así,
$$P_1 = \frac{V^2}{R_1} = \frac{(3.00 V)^2}{1.00 Ω} = 9.00 W$$Similarmente:
$$P_2 = \frac{V^2}{R_2} = \frac{(3.00 V)^2}{2.00 Ω} = 4.50 W$$ $$P_3 = \frac{V^2}{R_3} = \frac{(3.00 V)^2}{3.00 Ω} = 4.0 W$$(e) La potencia total también se puede calcular de varias maneras. Elegir $P = IV$ e ingresar los resultados de las corrientes totales:
$$P = IV = (6.00 A)(3.00 V) = 18.00 W$$Explicación
La potencia total disipada por los resistores también es de $18.00 W$:
$$P_1 + P_2 + P_3 = 9.0 0W + 4.50 W + 4.5 0W = 18.0 0W$$Observa que la potencia total disipada por los resistores es igual a la potencia suministrada por la fuente.
 Comprueba tu aprendizaje 10.3
Comprueba tu aprendizaje 10.3
 Comprueba tu aprendizaje 10.4
Comprueba tu aprendizaje 10.4
Vamos a resumir las principales características de los resistores en paralelo:
1. La resistencia equivalente se encuentra desde
$$R_{\textsf{eq}} = \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... + \frac{1}{R_{N-1}} + \frac{1}{R_N} \right) ^{-1} = \left( \sum_{i = 1}^{N} \frac{1}{R_i}\right)^{-1}$$y es más pequeño que cualquier resistencia individual en la combinación.
2. La caída de potencial a través de cada resistor en paralelo es la misma.
3. Los resistores paralelos no obtienen cada uno la corriente total; ellos lo dividen. La corriente que ingresa a una combinación paralela de resistores es igual a la suma de la corriente a través de cada resistor en paralelo.
En este capítulo, presentamos la resistencia equivalente de los resistores conectados en serie y los resistores conectados en paralelo. Puedes recordar que, en Capacitancia, presentamos la capacitancia equivalente de los condensadores conectados en serie y en paralelo. Los circuitos a menudo contienen condensadores y resistores. La resume las ecuaciones usadas para la resistencia equivalente y la capacitancia equivalente para conexiones en serie y paralelas.

Las conexiones más complejas de resistores a menudo son solo combinaciones de conexiones en serie y paralelas. Tales combinaciones son comunes, especialmente cuando se considera la resistencia del cable. En ese caso, la resistencia del cable está en serie con otras resistencias que están en paralelo.
Las combinaciones en serie y paralela se pueden reducir a una sola resistencia equivalente utilizando la técnica ilustrada en la . Varias partes pueden identificarse como conexiones en serie o paralelas, reducirse a sus resistencias equivalentes, y luego reducirse hasta que quede una sola resistencia equivalente.
El proceso es más lento que difícil. Aquí, notamos la resistencia equivalente como $R_{\textsf{eq}}$. En la figura se destaca: (a) El circuito original de cuatro resistores. (b) Paso 1: Las resistencias $R_3$ y $R_4$ están en serie y la resistencia equivalente es $R_{34} = 10 Ω$. (c) Paso 2: El circuito reducido muestra los resistores $R_2$ y $R_{34}$ en paralelo, con una resistencia equivalente de $R_{234} = 5 Ω$. (d) Paso 3: El circuito reducido muestra que $R_1$ y $R_{234}$ están en serie con una resistencia equivalente de $R_{1234} = 12 Ω$, que es la resistencia equivalente $R_{\textsf{eq}}$.
(e) El circuito reducido con una fuente de tensión de $V = 24 V$ con una resistencia equivalente de $R_{\textsf{eq}} = 12 Ω$. Esto da como resultado una corriente de $I = 2A$ desde la fuente de voltaje.

Ten en cuenta que los resistores $R_3$ y $R_4$ están en serie. Se pueden combinar en una sola resistencia equivalente. Un método de hacer un seguimiento del proceso es incluir los resistores como subíndices. Aquí el resistor equivalente de $R_3$ y $R_4$ es
$$R_{34} = R_3 + R_4 = 6 Ω + 4 Ω = 10 Ω.$$El circuito ahora se reduce a tres resistores, que se muestran en la (c). Redibujando, ahora vemos que los resistores $R_2$ y $R_{34}$ constituyen un circuito paralelo. Esos dos resistores se pueden reducir a un resistor equivalente:
$$R_{234} = \left(\frac{1}{R_2} + \frac{1}{R_{34}} \right)^{-1} = \left(\frac{1}{10 Ω} + \frac{1}{10 Ω} \right)^{-1}$$Este paso del proceso reduce el circuito a dos resistores, que se muestran en la (d). Aquí, el circuito se reduce a dos resistores, que en este caso están en serie. Estos dos resistores pueden reducirse a un resistor equivalente, que es el resistor equivalente del circuito:
$$R_{\textsf{eq}} = R_{1234} = R_1 + R_{234} = 7 Ω + 5 Ω = 12 Ω$$El objetivo principal del análisis de este circuito se alcanza, y el circuito ahora se reduce a una sola fuente de resistencia y una sola tensión.
Ahora podemos analizar el circuito. La corriente proporcionada por la fuente de voltaje es $I = \frac{V}{R_{\textsf{eq}}} = \frac{24 V}{12 Ω} = 2 A$.
Esta corriente se ejecuta a través del resistor $R_1$ y se designa como $I_1.$ La caída de potencial en $R_1$ se puede encontrar usando la ley de Ohm: $$V_1 = I_1R_1 = (2 A)(7 Ω) = 14 V$$
Mirando la Figura 10.15 (c), esto deja $24 V - 14 V = 10 V$ para caer a través de la combinación paralela de $R_2$ y $R_{34}$. La corriente a través de $R_2$ se puede encontrar usando la ley de Ohm:
$$I_2 = \frac{V_2}{R_2} = \frac{10 V}{10 Ω} = 1 A.$$Los resistores $R_3$ y $R_4$ están en serie, por lo que las corrientes $I_3$ e $I_4$ son iguales a
$$I_3 = I_4 = I - I_2 = 2 A - 1 A = 1 A$$Usando la ley de Ohm, podemos encontrar la caída de potencial a través de los dos últimas resistores. Las caídas de potencial son $V_3 = I_3R_3 = 6 V$ y $V_4 = I_4R_4 = 4 V$. El análisis final consiste en observar la potencia suministrada por la fuente de tensión y la potencia disipada por las resistencias. La potencia disipada por las resistencias es
$$P_1 = I_1^2R_1 = (2 A)^2(7 Ω) = 28 W$$ $$P_2 = I_2^2R_2 = (1 A)^2(10 Ω) = 10 W$$ $$P_3 = I_3^2R_3 = (1 A)^2(6 Ω) = 6 W$$ $$P_4 = I_4^2R_4 = (1 A)^2(4 Ω) = 4 W$$La energía total es constante en cualquier proceso. Por lo tanto, la potencia suministrada por la fuente de tensión es $P_s = IV = (2 A)(24 V) = 48 W$. Analizar la potencia suministrada al circuito y la potencia disipada por los resistores es una buena verificación de la validez del análisis; ellos deberían ser iguales.
Ejemplo 10.4
Combinando Circuitos en serie y en Paralelo
La muestra los resistores conectados en una combinación de serie y paralelo. Podemos considerar que $R_1$ es el resistor de los cables que conducen a $R_2$ y $R_3$. (a) Encuentra la resistencia equivalente del circuito. (b) ¿Cuál es la caída de potencial $V_1$ a través del resistor $R_1$? (c) Encuentra la corriente $I_2$ a través del resistor $R_2$. (d) ¿Qué potencia es disipada por $R_2$?
Estrategia
(a) Para encontrar la resistencia equivalente, primero encuentra la resistencia equivalente de la conexión paralela de $R_2$ y $R_3$. Luego usa este resultado para encontrar la resistencia equivalente de la conexión en serie con $R_1$.
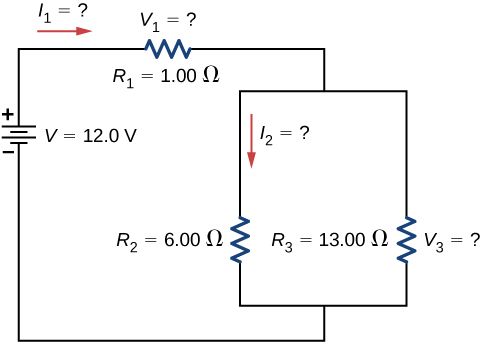
(b) La corriente a través de $R_1$ se puede encontrar usando la ley de Ohm y el voltaje aplicado. La corriente a través de $R_2$ es igual a la corriente de la batería. La caída de potencial $V_1$ a través del resistor $R_1$ (que representa la resistencia en los cables de conexión) se puede encontrar utilizando la ley de Ohm.
(c) La corriente a través de $R_2$ se puede encontrar usando la ley de Ohm $I_2 = V_2/R_2$. El voltaje en $R2$ se puede encontrar usando $V_2 = V - V_1$.
(d) Utilizando la ley de Ohm $(V_2 = I_2R_2)$, la potencia disipada por el resistor también se puede encontrar usando $P_2 = I_2^2R_2 = V_2^2/R_2$.
Solución
(a) Para encontrar la resistencia equivalente del circuito, observa que la conexión paralela de $R_2$ y $R_3$ está en serie con $R_1$, por lo que la resistencia equivalente es
Para encontrar la resistencia equivalente del circuito, observa que la conexión paralela de $R_2$ y $R_3$ está en serie con $R_1$, por lo que la resistencia equivalente es
$$R_{\textsf{eq}} = R_1 + \left(\frac{1}{R_2} + \frac{1}{R_3} \right)^{-1} = 1.00 Ω + \left(\frac{1}{6 Ω} + \frac{1}{13 Ω} \right)^{-1} = 5.10 Ω$$La resistencia total de esta combinación es intermedia entre la serie pura y los valores paralelos puros ($20.0 Ω$ y $0.804 Ω$, respectivamente).
(b) La corriente a través de $R_1$ es igual a la corriente suministrada por la batería: $$I_1 = I = \frac{V}{R_{\textsf{eq}}} = \frac{12.00 V}{5.10 Ω} = 2.35 A$$
El voltaje en $R_1$ es
$$V_1 = I_1R_1 = (2.35 A)(1 Ω) = 2.35 V$$La tensión aplicada a $R_2$ y $R_3$ es menor que la tensión suministrada por la batería en una cantidad $V_1$. Cuando la resistencia del cable es grande, puede afectar significativamente el funcionamiento de los dispositivos representados por $R_2$ y $R_3$.
(c) Para encontrar la corriente a través de $R_2$, primero debemos encontrar el voltaje aplicado. El voltaje a través de los dos resistores en paralelo es el mismo:
$$V_2 = V_3 = V - V_1 = 12.0 V - 2.35 V = 9.65 V$$Ahora podemos encontrar la corriente $I_2$ a través de la resistencia $R_2$ usando la ley de Ohm: $$I_2 = \frac{V_2}{R_2} = \frac{9.65 V}{6.00 Ω} = 1.61 A$$
La corriente es menor que los $2,00 A$ que fluyeron a través de $R_2$ cuando se conectó en paralelo a la batería en el ejemplo del circuito paralelo anterior.
(d) La potencia disipada por $R_2$ viene dada por $$P_2 = I_2^2R_2 = (1.61 A)^2(6.00 Ω) = 15.5 W$$
Explicación
El análisis de circuitos complejos a menudo se puede simplificar reduciendo el circuito a una fuente de voltaje y una resistencia equivalente. Incluso si el circuito completo no puede reducirse a una sola fuente de voltaje y una sola resistencia equivalente, se pueden reducir partes del circuito, lo que simplifica enormemente el análisis.
 Comprueba tu aprendizaje 10.5
Comprueba tu aprendizaje 10.5
Una implicación de este ejemplo es que la resistencia en los cables reduce la corriente y la potencia entregada a un resistor. Si la resistencia del cable es relativamente grande, como en un cable de extensión gastado (o muy largo), esta pérdida puede ser significativa. Si se dibuja una corriente grande, la caída de IR en los cables también puede ser significativa y es evidente por el calor generado en el cable.
Por ejemplo, cuando estás hurgando en el refrigerador y el motor se enciende, la luz del refrigerador se atenúa momentáneamente. De manera similar, puedes ver que la luz del compartimiento de pasajeros se atenúa cuando enciendes el motor de tu automóvil (aunque esto puede deberse a la resistencia dentro de la misma batería).
Lo que está sucediendo en estas situaciones de alta corriente se ilustra en la .
El dispositivo representado por $R_3$ tiene una resistencia muy baja, por lo que cuando se enciende, fluye una gran corriente. Esta mayor corriente causa una mayor caída de $IR$ en los cables representados por $R_1$, reduciendo el voltaje a través de la bombilla (que es $R_2$), que luego se atenúa notablemente.
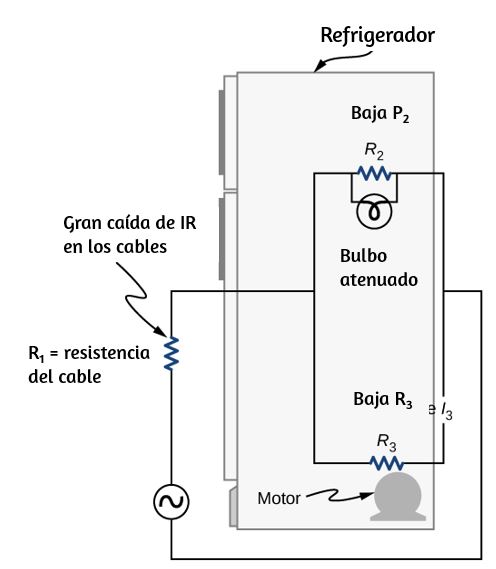
Ejemplo 10.6
Combinando Circuitos en Serie y Paralelos
Dos resistores conectados en serie ($R_1$, $R_2$) están conectados a dos resistores que están conectados en paralelo ($R_3$, $R_4$). La combinación serie-paralelo está conectada a una batería. Cada resistor tiene una resistencia de $10.00 Ohms$. Los cables que conectan los resistores y la batería tienen una resistencia insignificante. Una corriente de $2.00 Amps$ pasa a través del resistor $R_1$. ¿Cuál es el voltaje suministrado por la fuente de voltaje?
Estrategia
Usa los pasos de la estrategia anterior de resolución de problemas para encontrar la solución para este ejemplo.
Solución
1. Dibuja un diagrama de circuito claro ().
2. Lo desconocido es el voltaje de la batería. Para encontrar el voltaje suministrado por la batería, se debe encontrar la resistencia equivalente.

3. En este circuito, ya sabemos que los resistores $R_1$ y $R_2$ están en serie y los resistores $R_3$ y $R_4$ están en paralelo.
La resistencia equivalente de la configuración paralela de los resistores $R_3$ y $R_4$ está en serie con la configuración en serie de los resistores $R_1$ y $R_2$.
4. La tensión suministrada por la batería se puede encontrar multiplicando la corriente de la batería y la resistencia equivalente del circuito. La corriente de la batería es igual a la corriente a través de $R_1$ y es igual a $2.00 A$. Necesitamos encontrar la resistencia equivalente al reducir el circuito. Para reducir el circuito, primero considera los dos resistores en paralelo. La resistencia equivalente es $R_{34} = (\frac{1}{10.00 Ω} + \frac{1}{10.00 Ω})^{-1} = 5.00 Ω$. Esta combinación en paralelo está en serie con los otros dos resistores, por lo que la resistencia equivalente del circuito es $R_{\textsf{eq}} = R_1 + R_2 + R_{34} = 25.00 Ω$. El voltaje suministrado por la batería es por lo tanto $V = IR_{\textsf{eq}} = 2.00 A 25.00 Ω) = 50.00 V$.
5. Una forma de verificar la consistencia de tus resultados es calcular la potencia suministrada por la batería y la potencia disipada por los resistores. La potencia suministrada por la batería es $P_{\textsf{bat}} = IV = 100.0 0W$.
Como están en serie, la corriente a través de $R_2$ es igual a la corriente a través de $R_1$. Como $R_3 = R_4$, la corriente a través de cada uno será $1.00$ amperios. La potencia disipada por los resistores es igual a la suma de la potencia disipada por cada resistor:
$$\begin{split} P &= I_1^2R_1 + I_2^2R_2 + I_3^2R_3 + I_4^2R_4 \\ &= 40.00 W + 40.00 W + 10.00 W + 10.00 W = 100.00 W \end{split}$$Dado que la potencia disipada por las resistencias es igual a la potencia suministrada por la batería, nuestra solución parece consistente.
Explicación
Si un problema tiene una combinación en serie y paralelo, como en este ejemplo, se puede reducir en pasos usando la estrategia anterior de resolución de problemas y considerando grupos individuales de conexiones en serie o paralelas. Al encontrar $R_{\textsf{eq}}$ para una conexión paralela, el recíproco debe tomarse con cuidado. Además, las unidades y los resultados numéricos deben ser razonables. La resistencia en serie equivalente debería ser mayor, mientras que la resistencia paralela equivalente debería ser menor, por ejemplo. La potencia debe ser mayor para los mismos dispositivos en paralelo en comparación con los en serie, y así sucesivamente.
Con la siguiente escena interactiva de PhET Simulaciones, resuelve el problema anterior, si la corriente que pasa por $R_1$ es de $0.72 Amps$. En la siguiente imagen, lo hemos resuelto para $1.08 A$ (haz clic sobre la imagen para ampliarla).
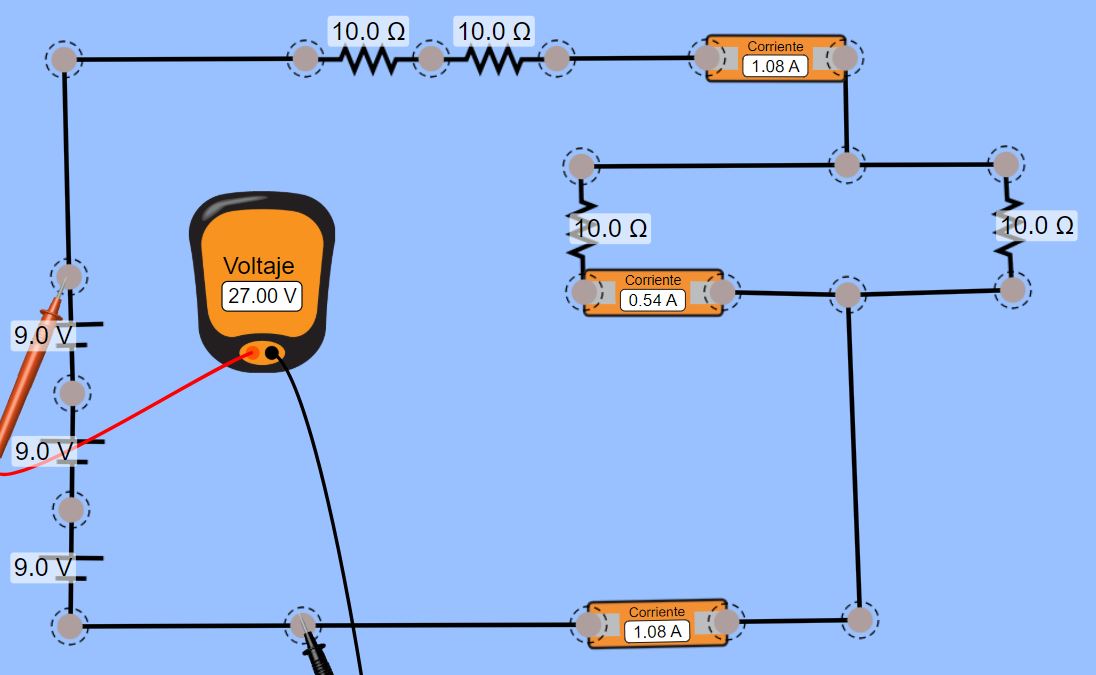
Acabamos de ver que algunos circuitos se pueden analizar reduciendo un circuito a una única fuente de voltaje y una resistencia equivalente. Muchos circuitos complejos no pueden analizarse con las técnicas en serie y en paralelo desarrolladas en las secciones anteriores. En esta sección, discutiremos sobre el uso de las reglas de Kirchhoff para analizar circuitos más complejos. Por ejemplo, el circuito de la se conoce como circuito multi-loop o multi-ciclo, que consiste en uniones. Una unión, también conocida como un nodo, es una conexión de tres o más cables. En este circuito, los métodos anteriores no se pueden utilizar, porque no todos los resistores están en series claras o configuraciones paralelas que se pueden reducir. Los resistores $R_1$ y $R_2$ están en serie y se pueden reducir a una resistencia equivalente. Lo mismo es cierto para los resistores $R_4$ y $R_5$. ¿Pero qué haces después?
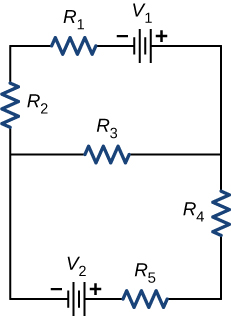
Aunque este circuito no se puede analizar utilizando los métodos ya aprendidos, se pueden usar dos reglas de análisis de circuitos para analizar cualquier circuito, simple o complejo. Las reglas se conocen como las reglas de Kirchhoff, en honor a su inventor Gustav Kirchhoff (1824-1887).
Las reglas de Kirchhoff
Ahora proporcionamos explicaciones de estas dos reglas, seguidas por sugerencias para resolver problemas para aplicarlas y un ejemplo trabajado que las usa.
La primera regla de Kirchhoff (la regla de unión) se aplica a la carga que ingresa y sale de una unión (). Como se indicó anteriormente, una unión, o nodo, es una conexión de tres o más cables.
La corriente es el flujo de carga, y la carga se conserva; por lo tanto, cualquier carga que fluya hacia la unión debe fluir.

Aunque es una simplificación excesiva, se puede hacer una analogía con las tuberías de agua conectadas en una unión de tuberías. Si los cables de la fueron reemplazados por tuberías de agua y se supuso que el agua es incompresible, el volumen de agua que fluye hacia la unión debe ser igual al volumen de agua que sale de la unión.
La segunda regla de Kirchhoff (la regla del ciclo) se aplica a las diferencias de potenciales. La regla del bucle se expresa en términos de potencial $V$ en lugar de energía potencial, pero los dos están relacionados desde $U = qV$.
En un circuito cerrado, independientemente de la energía que suministre una fuente de tensión, los dispositivos en el circuito deben transferir la energía a otras formas, ya que no hay otras formas en que la energía pueda transferirse al circuito o fuera de él. La regla del bucle de Kirchhoff establece que la suma algebraica de las diferencias de potencial, incluida la tensión suministrada por las fuentes de tensión y los elementos resistivos, en cualquier bucle debe ser igual a cero. Por ejemplo, considera un bucle simple sin uniones, como en la .
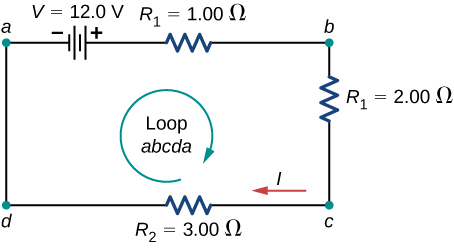
El circuito consiste en una fuente de voltaje y tres resistores de carga externos. Las etiquetas $a, b, c$ y $d$ sirven como referencias, y no tienen otro significado. La utilidad de estas etiquetas se hará evidente pronto. El lazo se designa como Loop $abcda$, y las etiquetas ayudan a realizar un seguimiento de las diferencias de voltaje a medida que viajamos por el circuito. Comienza en el punto $a$ y viaja al punto $b$. El voltaje de la fuente de voltaje se agrega a la ecuación y la caída de potencial del resistor $R_1$ se resta.
Desde el punto $b$ hasta $c$, se resta la caída de potencial a través de $R_2.$ Desde $c$ hasta $d$, se resta la caída potencial a través de $R_3$. Desde los puntos $d$ hasta $a$, nada se hace porque no hay componentes.
La muestra un gráfico de la tensión a medida que viajamos por el circuito. El voltaje aumenta a medida que cruzamos la batería, mientras que el voltaje disminuye a medida que viajamos a través de un resistor. La caída de potencial, o cambio en el potencial eléctrico, es igual a la corriente a través de la resistencia multiplicada por la resistencia del resistor. Como los cables tienen una resistencia despreciable, el voltaje permanece constante a medida que cruzamos los cables que conectan los componentes.
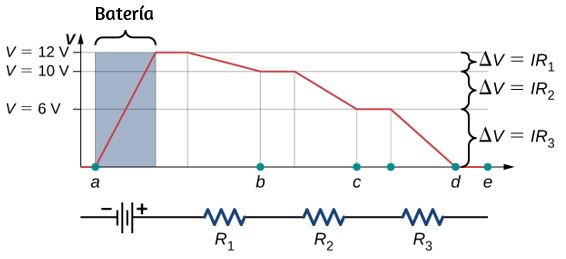
Entonces la regla del ciclo de Kirchhoff dice
$$V - IR_1 - IR_2 - IR_3 = 0.$$La ecuación del ciclo se puede usar para encontrar la corriente a través del bucle:
$$I = \frac{V}{R_1 + R_2 + R_3} = \frac{12.00 V}{1.00 Ω + 2.00 Ω + 3.00 Ω} = 2.00 A.$$Este ciclo podría haberse analizado utilizando los métodos anteriores, pero demostraremos el poder del método de Kirchhoff en la siguiente sección.
Al aplicar las reglas de Kirchhoff, generamos un conjunto de ecuaciones lineales que nos permiten encontrar los valores desconocidos en los circuitos. Estas pueden ser corrientes, voltajes o resistencias. Cada vez que se aplica una regla, produce una ecuación. Si hay tantas ecuaciones independientes como incógnitas, entonces el problema se puede resolver. El uso del método de análisis de Kirchhoff requiere varios pasos, como se detalla en el siguiente procedimiento.
Estrategia de resolución de problemas: Reglas de Kirchhoff
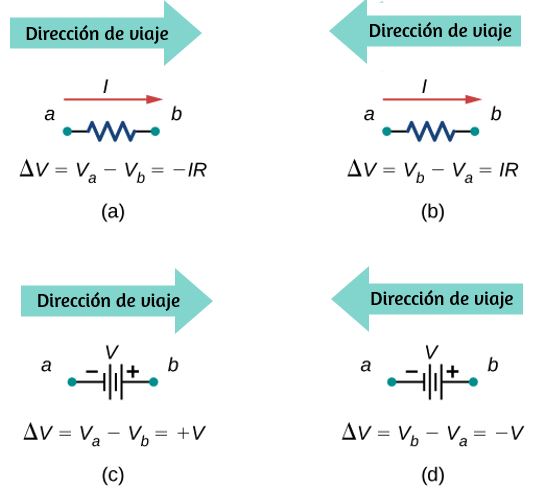
Examinemos algunos pasos en este procedimiento más de cerca. Al ubicar las uniones en el circuito, no tes preocupes por la dirección de las corrientes. Si la dirección del flujo de corriente no es obvia, la elección de cualquier dirección es suficiente siempre que al menos una corriente apunte a la unión y al menos una corriente indique la salida. Si la flecha está en la dirección opuesta al flujo de corriente convencional, el resultado para la corriente en cuestión será negativo, pero la respuesta seguirá siendo correcta.
La cantidad de nodos depende del circuito. Cada corriente debe incluirse en un nodo y, por lo tanto, debe incluirse en al menos una ecuación de unión. No incluyas nodos que no sean linealmente independientes, es decir, nodos que contengan la misma información.
Considera la . Hay dos uniones en este circuito: Cruce $b$ y Cruce $e$. Los puntos $a, c, d$ y $f$ no son uniones porque una unión debe tener tres o más conexiones.
La ecuación para la unión $b$ es $I1 = I2 + I3$, y la ecuación para la unión $e$ es $I2 + I3 = I1$. Estas son ecuaciones equivalentes, por lo que es necesario guardar solo una de ellas.
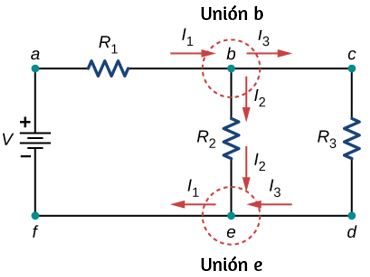
Al elegir los ciclos en el circuito, necesitas suficientes ciclos para que cada componente esté cubierto una vez, sin repetir ciclo. La muestra cuatro opciones para ciclos para resolver un circuito de muestra; las opciones (a), (b) y (c) tienen una cantidad suficiente de ciclos para resolver el circuito completo. La opción (d) refleja más ciclos de los necesarios para resolver el circuito.
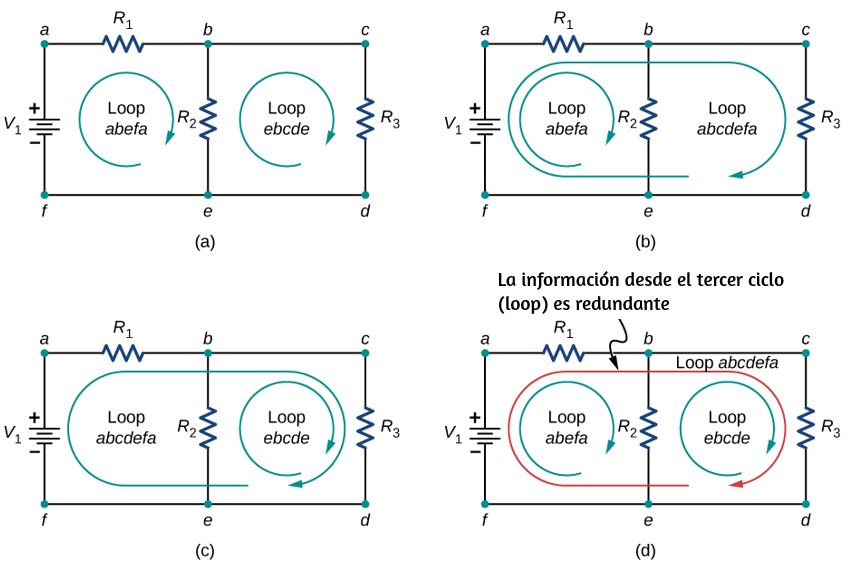
Considera el circuito en la (a). Analicemos este circuito para encontrar la corriente a través de cada resistor. Primero, etiqueta el circuito como se muestra en la parte (b).
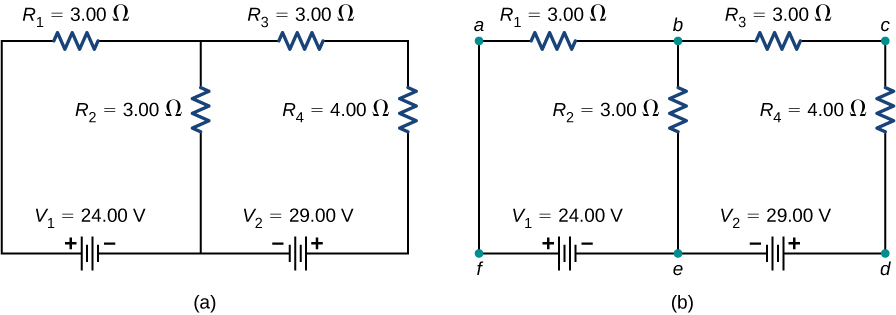
Luego, determina las uniones. En este circuito, los puntos $b$ y $e$ tienen tres cables conectados, lo que los convierte en uniones. Comienza a aplicar la regla de unión de Kirchhoff ($\sum I_{\textsf{in}} = \sum I_{\textsf{out}})$ dibujando flechas que representan las corrientes y etiquetando cada flecha, como se muestra en la (b). La unión $b$ muestra que $I_1 = I_2 + I_3$ y la unión e muestra que $I_2 + I_3 = I_1$. Como la unión e proporciona la misma información de la unión $b$, puede descartarse. Este circuito tiene tres incógnitas, por lo que necesitamos tres ecuaciones linealmente independientes para analizarlo.
Luego tenemos que elegir los ciclos. En la , el ciclo (loop) abefa incluye la fuente de tensión $V_1$ y los resistores $R_1$ y $R_2$. El ciclo comienza en el punto a, luego recorre los puntos $b, e$, y $f$, y luego vuelve al punto $a$. El segundo ciclo, Loop $ebcde$, comienza en el punto $e$ e incluye las resistencias $R_2$ y $R_3$, y la fuente de voltaje $V_2$.
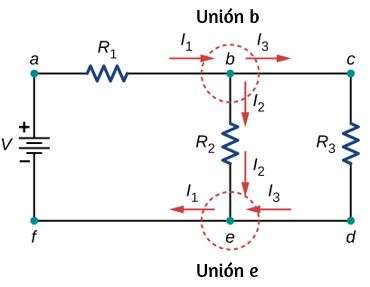
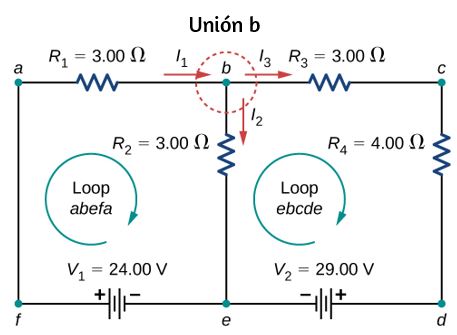
Ahora podemos aplicar la regla del ciclo de Kirchhoff, usando el mapa en la . Comenzando en el punto a y moviéndose al punto b, el resistor $R_1$ se cruza en la misma dirección que el flujo de corriente $I_1$, por lo que se resta la caída de potencial $I_1R_1$. Al pasar del punto $b$ al punto $e$, la resistencia $R_2$ se cruza en la misma dirección que el flujo de corriente $I_2$, por lo que se resta la caída de potencial $I_2R_2$. Al pasar del punto $e$ al punto $f$, la fuente de tensión $V_1$ se cruza desde el terminal negativo al terminal positivo, por lo que se agrega $V_1$. No hay componentes entre los puntos $f$ y $a$. La suma de las diferencias de voltaje debe ser igual a cero:
$$\textsf{Ciclo } abefa: −I_1R_1 − I_2R_2 + V_1 = 0 o V_1 = I_1R_1 + I_2R_2$$Finalmente, verificamos el ciclo ebcde. Comenzamos en el punto $e$ y avanzamos al punto $b$, cruzando $R_2$ en la dirección opuesta al flujo de corriente $I_2$. Se agrega el potencial de caída de $I_2R_2$. A continuación, cruzamos $R_3$ y $R_4$ en la misma dirección que el flujo de corriente $I_3$ y restamos las caídas de potencial $I_3R_3$ e $I_3R_4$. Ten en cuenta que la corriente es la misma a través de los resistores $R_3$ y $R_4$, porque están conectadas en serie. Finalmente, la fuente de voltaje se cruza desde el terminal positivo al terminal negativo, y la fuente de voltaje $V_2$ se resta. La suma de estas diferencias de voltaje es igual a cero y produce la ecuación de bucle
$$\textsf{Ciclo } ebcde: I_2R_2 − I_3(R_3 + R_4) − V_2 = 0$$Ahora tenemos tres ecuaciones, que podemos resolver para las tres incógnitas.
(1) Unión $b: I_1 − I_2 − I_3=0$.
(2) Ciclo $abefa: I_1R_1 + I_2R_2 = V1$.
(3) Ciclo $ebcde: I_2R_2 − I_3(R_3 + R_4) = V_2$.
Para resolver las tres ecuaciones para las tres corrientes desconocidas, comienza por eliminar la corriente $I_2$. Primero agrega la ecuación (1) veces $R_2$ a la ecuación (2). El resultado se etiqueta como ecuación (4):
$$(R_1 + R_2)I_1 − R_2I_3 = V_1$$ $$(4) 6ΩI_1 − 3ΩI_3 = 24V$$Luego, resta la ecuación (3) de la ecuación (2). El resultado se etiqueta como ecuación (5):
$$I_1R_1 + I_3(R_3 + R_4) = V_1 − V_2$$ $$(5) 3ΩI_1 + 7ΩI_3 = −5V$$Podemos resolver la ecuaciones (4) y (5) para la corriente $I_1$. Agregar siete veces la ecuación (4) y tres veces la (5) da como resultado $51ΩI_1 = 153V$, o $I_1 = 3.00 A$. Usando la ecuación (4) da como resultado $I_3 = -2.00 A$. Finalmente, la ecuación (1) produce $I_2 = I_1 - I_3 = 5.00 A$. Una forma de comprobar que las soluciones son consistentes es verificar la potencia suministrada por las fuentes de tensión y la potencia disipada por los resistores:
$$P_{\textsf{in}} =I_1V_1 + I_3V_2 = 130 W,$$ $$P_{\textsf{out}} =I_1^2R_1 + I_2^2R_2 + I_3^2R_2 + I_3^2R_4 = 130 W.$$Observa que la solución para el $I_3$ la corriente es negativa. Esta es la respuesta correcta, pero sugiere que la flecha originalmente dibujada en el análisis de la unión es la dirección opuesta al flujo de corriente convencional. La potencia suministrada por la segunda fuente de tensión es $58 W$ y no $-58 W$.
Ejemplo 10.6
Cálculo de corriente utilizando las reglas de Kirchhoff
Encuentra las corrientes que fluyen en el circuito de la .
Estrategia
Este circuito es lo suficientemente complejo como para que las corrientes no puedan ser encontradas usando la ley de Ohm y las técnicas en serie paralelas: es necesario usar las reglas de Kirchhoff. Las corrientes se han etiquetado como $I_1$, $I_2$ e $I_3$ en la figura, y se han hecho suposiciones sobre sus direcciones. Las ubicaciones en el diagrama han sido etiquetadas con letras $a$ a $h$. En la solución, aplicamos las reglas de unión y del ciclo, buscando tres ecuaciones independientes que nos permitan hallar las tres corrientes desconocidas.
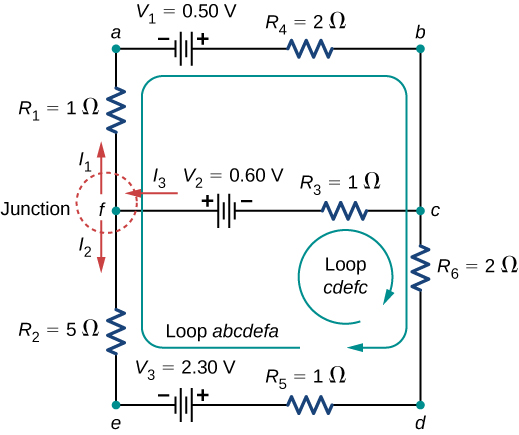
Solución
Al aplicar las reglas de unión y del ciclo se obtienen las siguientes tres ecuaciones. Tenemos tres incógnitas, por lo que se requieren tres ecuaciones.
Unión $c: I_1 + I_2 = I_3$.
Ciclo $abcdefa: I_1(R_1 + R_3) - I_2(R_2 + R_5 + R_6) = V_1 - V_3$.
Ciclo $cdefc: I_2(R_2 + R_5 + R_6) + I_3R_3 = V_2 + V_3$.
Simplifica las ecuaciones colocando las incógnitas en un lado de las ecuaciones.
Unión $c: I_1 + I_2 - I_3 = 0$.
Ciclo $abcdefa: I_1(3 Ω) - I_2(8 Ω) = 0.5 V - 2.30 V$.
Ciclo $cdefc: I_2(8 Ω) + I_3(1 Ω) = 0.6 V + 2.30 V$.
Simplifica las ecuaciones. La primera ecuación de ciclo se puede simplificar dividiendo ambos lados por $3.00$. La ecuación del segundo ciclo se puede simplificar dividiendo ambos lados por $6,00$.
Ciclo $c: I_1 + I_2 - I_3 = 0$.
Ciclo $abcdefa: I_1(3 Ω) - I_2(8 Ω) = - 1.8V$.
Ciclo $cdefc: I_2(8 Ω) + I_3(1 Ω) = 2.9 V$.
Los resultados son
$$I_1 = 0.20 A, I_2 = 0.30 A, I_3 = 0.50 A.$$Explicación
Un método para verificar los cálculos es calcular la potencia disipada por los resistores y la potencia suministrada por las fuentes de tensión:
$$P_{R_1} = I_1^2R_1 = 0.04 W$$ $$P_{R_2} = I_2^2R_2 = 0.45 W$$ $$P_{R_3} = I_3^2R_3 = 0.25 W$$ $$P_{R_4} = I_4^2R_4 = 0.08 W$$ $$P_{R_5} = I_5^2R_5 = 0.09 W$$ $$P_{R_6} = I_6^2R_6 = 0.18 W$$ $$P_{\textsf{disipada}} = 1.09 W$$ $$P_{\textsf{fuente}} = I_1V_1 + I_2V_3 + I_3V_3 = 0.10 W + 0.69 W + 0.30 W = 1.09 W$$La potencia suministrada es igual a la potencia disipada por los resistores.
 Comprueba tu aprendizaje 10.6
Comprueba tu aprendizaje 10.6
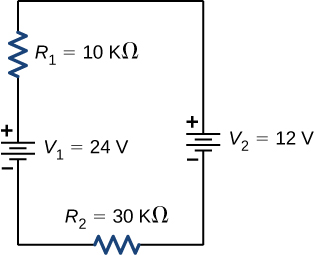
Ejemplo 10.7
Cálculo de la corriente utilizando las reglas de Kirchhoff
Encuentra la corriente que fluye en el circuito en la .
Estrategia
Este circuito puede analizarse usando las reglas de Kirchhoff. Solo hay un ciclo y no hay nodos. Elige la dirección del flujo de corriente. Para este ejemplo, usaremos la dirección horaria del punto a al punto b. Considera el ciclo abcda y usa la para escribir la ecuación de ciclo. Ten en cuenta que, de acuerdo con la , se agregará la batería $V_1$ y se restará la batería $V_2$.
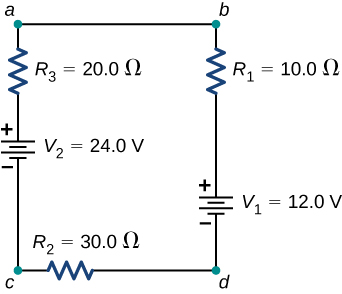
Solución
Al aplicar la regla de la unión se obtienen las siguientes tres ecuaciones. Tenemos una incognita, por lo que se requiere una ecuación:
$$\textsf{Ciclo } abcda: -IR_1 - V_1 - IR_2 + V_2 - IR_3 = 0.$$Simplifica las ecuaciones colocando las incógnitas en un lado de las ecuaciones. Usa los valores dados en la figura.
$$I(R_1 + R_2 + R_3) = V_2- V_1$$ $$I = \frac{V_2 - V_1}{R_1 + R_2 + R_3} = \frac{24 V - 12 V}{10.0 Ω + 30.0 Ω + 10.0 Ω} = 0.20 A.$$Explicación
La potencia disipada o consumida por el circuito es igual a la potencia suministrada al circuito, pero observa que la corriente en la batería $V_1$ fluye a través de la batería desde el terminal positivo al terminal negativo y consume potencia.
$$P_{R_1} = I^2R_1 = 0.40 W$$ $$P_{R_2} = I^2R_2 = 1.20 W$$ $$P_{R_3} = I^2R_3 = 0.8 W$$ $$P_{V_1} = IV_1 = 2.40 W$$ $$P_{\textsf{disipada}} = 4.80 W$$ $$P_{\textsf{fuente}} = IV_2 = 4.80 W$$La potencia suministrada es igual a la potencia disipada por los resistores y consumida por la batería $V_1$.
 Comprueba tu aprendizaje 10.7
Comprueba tu aprendizaje 10.7
Muchos dispositivos requieren más de una batería. Se pueden conectar múltiples fuentes de voltaje, como baterías, en configuraciones en serie, configuraciones paralelas o una combinación de ambas.
En serie, el terminal positivo de una batería está conectado al terminal negativo de otra batería. Se puede conectar en serie cualquier cantidad de fuentes de voltaje, incluidas las baterías. En la se muestran dos baterías conectadas en serie. El uso de la regla del ciclo de Kirchhoff para el circuito en la parte (b) da el resultado.
$$ε_1 − Ir_1 + ε_2 − Ir_2 − IR = 0,$$ $$[(ε_1 + ε_2) − I(r_1 + r_2)] − IR = 0$$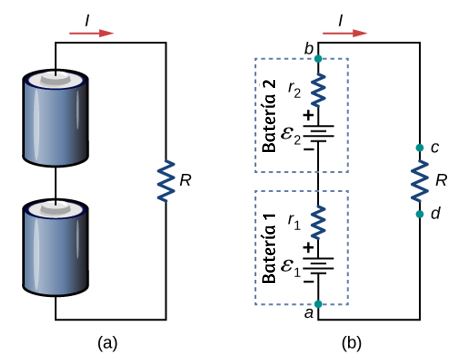
Cuando las fuentes de tensión están en serie, sus resistencias internas se pueden sumar juntas y sus emfs se pueden sumar para obtener los valores totales. Las conexiones en serie de fuentes de tensión son comunes, por ejemplo, en linternas, juguetes y otros dispositivos. Usualmente, las celdas están en serie para producir una fem total más grande. En la , el voltaje del terminal es
$$\begin{split} V_{\textsf{terminal}} &= (ε_1 − Ir_1) + (ε_2 − Ir_2) = [(ε_1 + ε_2) − I(r_1 + r_2)] \\ &= (ε_1 + ε_2) + I_{req} \end{split}$$Observa que la misma corriente $I$ se encuentra en cada batería porque están conectadas en serie. La desventaja de las conexiones en serie de las celdas es que sus resistencias internas son aditivas.
Las baterías están conectadas en serie para aumentar el voltaje suministrado al circuito. Por ejemplo, una linterna LED puede tener dos pilas AAA, cada una con un voltaje de terminal de $1.5 V$, para proporcionar $3.0 V$ a la linterna.
Se puede conectar cualquier cantidad de baterías en serie. Para $N$ baterías en serie, el voltaje del terminal es igual a
donde la resistencia equivalente es $\displaystyle r_{\textsf{eq}} \sum_{i = 1}^{N} r_i$
Cuando una carga se coloca a través de fuentes de voltaje en serie, como en la figura 10.32, podemos encontrar la corriente:
$$(ε_1 − Ir_1) + (ε_2 − Ir_2) = IR,$$ $$Ir_1 + Ir_2 + IR = ε_1 + ε_2,$$ $$I = \frac{ε_1 + ε_2}{r_1 + r_2 + R}$$Como se esperaba, las resistencias internas aumentan la resistencia equivalente.
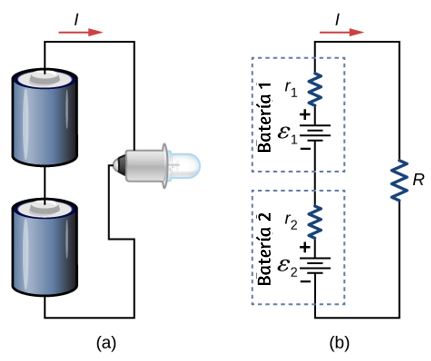
Las fuentes de voltaje, como las baterías, también se pueden conectar en paralelo. La muestra dos baterías con emfs idénticas en paralelo y conectadas a una resistencia de carga. Cuando las baterías se conectan en paralelo, los terminales positivos se conectan entre sí y los terminales negativos se conectan entre sí, y la resistencia de carga se conecta a los terminales positivo y negativo. Normalmente, las fuentes de voltaje en paralelo tienen emfs idénticas. En este caso simple, dado que las fuentes de voltaje están en paralelo, la fem total es igual a la fem individual de cada batería.
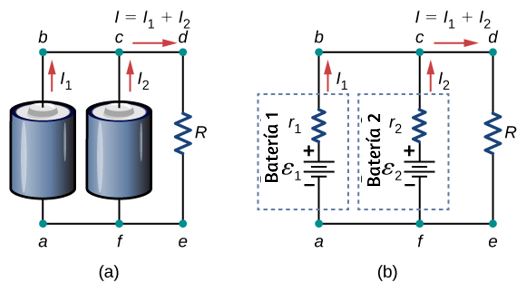
Considera el análisis de Kirchhoff del circuito en la (b). Hay dos ciclos y un nodo en el punto $b$ y $ε = ε_1 = ε_2$.
Nodo $b: I_1 + I_2 - I = 0$.
Ciclo $abcfa$: $$ε − I_1r_1 + I_2r_1 − ε = 0$$
$$I_1r_1 = I_2r_2$$Ciclo $fcdef$: $$ε_2 − I_2r_2 − IR = 0$$
$$ε − I_2r_2 − IR = 0$$La solución de la corriente a través del resistor de carga da como resultado $I = \frac{ε}{r_{\textsf{eq}} + R}$, donde $r_{\textsf{eq}} = (1/r_1 + 1/r_2)^{-1}$. El voltaje del terminal es igual a la caída de potencial a través del resistor de carga $IR = \frac{ε}{r_{\textsf{eq}} + R}$. La conexión en paralelo reduce la resistencia interna y por lo tanto puede producir una corriente más grande.
Se puede conectar cualquier cantidad de baterías en paralelo. Para $N$ baterías en paralelo, el voltaje del terminal es igual a
donde la resistencia equivalente es $\displaystyle r_{\textsf{eq}} = \left(\sum_{i = 1}^{N} \frac{1}{r_i} \right)^{-1}$
Como ejemplo, algunos camiones diesel usan dos baterías de $12 V$ en paralelo; producen un fem total de $12 V$ pero pueden entregar la mayor corriente necesaria para arrancar un motor diesel.
En resumen, la tensión del terminal de las baterías en serie es igual a la suma de las emfs individuales menos la suma de las resistencias internas por la corriente. Cuando las baterías se conectan en paralelo, generalmente tienen igual fem y la tensión del terminal es igual a la fem menos la resistencia interna equivalente por la corriente, donde la resistencia interna equivalente es menor que las resistencias internas individuales. Las baterías están conectadas en serie para aumentar el voltaje del terminal a la carga. Las baterías están conectadas en paralelo para aumentar la corriente a la carga.
Otro ejemplo que trata con múltiples fuentes de voltaje es el de las combinaciones de celdas solares conectadas en serie y combinaciones en paralelo para producir un voltaje y corriente deseados. La generación fotovoltaica, que es la conversión de la luz solar directamente en electricidad, se basa en el efecto fotoeléctrico. El efecto fotoeléctrico está más allá del alcance de este capítulo, pero en general, los fotones que golpean la superficie de una celda solar crean una corriente eléctrica en la celda.
La mayoría de las celdas solares están hechas de silicio puro. La mayoría de las celdas individuales tienen una salida de voltaje de aproximadamente $0.5 V$, mientras que la salida de corriente es una función de la cantidad de luz solar que cae sobre la celda (la radiación solar incidente conocida como la insolación). Bajo la luz del sol del mediodía brillante, una corriente por unidad de área de aproximadamente $100 mA/cm^2$ de área de superficie de celda es producida por las típicas celdas de un solo cristal.
Las celdas solares individuales están conectadas eléctricamente en módulos para satisfacer las necesidades de energía eléctrica.
Se pueden conectar juntas en serie o en paralelo, conectadas como las baterías discutidas anteriormente. Un conjunto o módulo de celdas solares generalmente consta de entre $36$ y $72$ celdas, con una potencia de salida de $50 W$ a $140 W$.
Las celdas solares, como las baterías, proporcionan un voltaje de corriente continua (CC). La corriente de una fuente de voltaje de cd es unidireccional. La mayoría de los electrodomésticos necesitan un voltaje de corriente alterna (CA).
La ley de Ohm y el método de Kirchhoff son útiles para analizar y diseñar circuitos eléctricos, proporcionándole voltajes, corriente y resistencia a través de los componentes que componen el circuito. Para medir estos parámetros se requieren instrumentos, y estos instrumentos se describen en esta sección.
Mientras que los voltímetros miden la tensión, los amperímetros miden la corriente. Algunos de los contadores en tableros de automóviles, cámaras digitales, teléfonos celulares y amplificadores-sintonizadores son en realidad voltímetros o amperímetros (). La construcción interna del más simple de estos medidores y la forma en que están conectados al sistema que monitorean proporcionan una mayor comprensión de las aplicaciones de conexiones en serie y paralelas.

Para medir la corriente a través de un dispositivo o componente, el amperímetro se coloca en serie con el dispositivo o componente. Se usa una conexión en serie porque los objetos en serie tienen la misma corriente que los atraviesa (Observa la , donde el amperímetro está representado por el símbolo $A$).
Los amperímetros necesitan tener una resistencia muy baja, una fracción de miliohm. Si la resistencia no es insignificante, colocar el amperímetro en el circuito cambiaría la resistencia equivalente del circuito y modificaría la corriente que se está midiendo.
Como la corriente en el circuito viaja a través del medidor, los amperímetros normalmente contienen un fusible para proteger el medidor del daño de las corrientes que son demasiado altas.
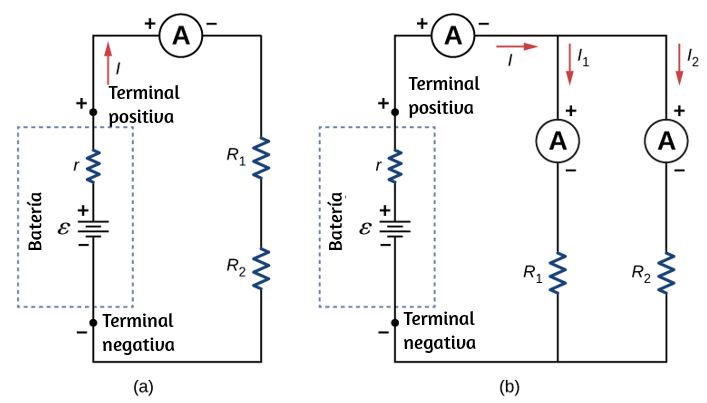
Un voltímetro está conectado en paralelo con cualquier dispositivo que esté midiendo. Se usa una conexión paralela porque los objetos en paralelo experimentan la misma diferencia de potencial (Observa la , donde el voltímetro está representado por el símbolo $V$).
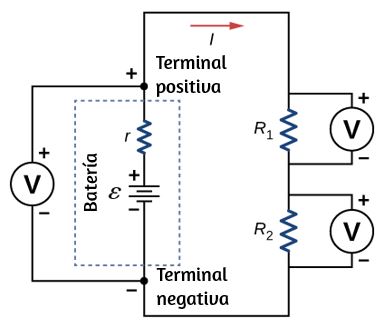
Como los voltímetros están conectados en paralelo, el voltímetro debe tener una resistencia muy grande. Los voltímetros digitales convierten la tensión analógica en un valor digital para mostrar en una lectura digital ().
Los voltímetros económicos tienen resistencias del orden de $RM = 10 MΩ$, mientras que los voltímetros de alta precisión tienen resistencias del orden de $RM = 10 GΩ$. El valor de la resistencia puede variar, dependiendo de la escala que se use en el medidor.

Puedes encontrar dos tipos de medidores en el laboratorio de física: analógico y digital. El término "analógico" se refiere a señales o información representada por una cantidad física continuamente variable, como voltaje o corriente.
Un medidor analógico utiliza un galvanómetro, que es esencialmente una bobina de cable con una pequeña resistencia, en un campo magnético, con un puntero conectado que apunta a una escala. La corriente fluye a través de la bobina, haciendo que la bobina gire. Para usar el galvanómetro como un amperímetro, se coloca una pequeña resistencia en paralelo con la bobina. Para un voltímetro, se coloca una resistencia grande en serie con la bobina.
Un medidor digital utiliza un componente denominado convertidor analógico a digital ($A$ a $D$) y expresa la corriente o voltaje como una serie de los dígitos $0$ y $1$, que se utilizan para ejecutar una pantalla digital. La mayoría de los medidores analógicos han sido reemplazados por medidores digitales.
 Comprueba tu aprendizaje 10.8
Comprueba tu aprendizaje 10.8
Un ohmímetro es un instrumento utilizado para medir la resistencia de un componente o dispositivo. El funcionamiento del ohmímetro se basa en la ley de Ohm. Los ohmímetros tradicionales contenían una fuente de tensión interna (como una batería) que se conectaría a través del componente a probar, produciendo una corriente a través del componente. Luego se usó un galvanómetro para medir la corriente y la resistencia se dedujo usando la ley de Ohm.
Los medidores digitales modernos usan una fuente de corriente constante para pasar corriente a través del componente, y se mide la diferencia de voltaje en todo el componente. En cualquier caso, la resistencia se mide usando la ley de Ohm $(R = V/I)$, donde se conoce el voltaje y se mide la corriente, o se conoce la corriente y se mide el voltaje.
El componente de interés debe aislarse del circuito; de lo contrario, medirá la resistencia equivalente del circuito. Un ohmímetro nunca debe conectarse a un circuito "vivo", uno con una fuente de voltaje conectada y corriente que lo atraviesa. Hacerlo puede dañar el medidor.
Retomamos la escena interactiva de PhET Simulaciones, para que pueda construir circuitos con resistores, fuentes de voltaje, amperímetros y voltímetros para poner a prueba tu conocimiento del diseño de circuitos.
Cuando utilizas una cámara de flash, tarda unos segundos en cargar el condensador (capacitor) que alimenta el flash. El flash de luz descarga el condensador en una pequeña fracción de segundo. ¿Por qué la carga lleva más tiempo que la descarga?
Esta pregunta y varios otros fenómenos que implican cargar y descargar condensadores se discuten en este módulo.
Un circuito RC es un circuito que contiene resistencia y capacitancia. Tal como hemos visto, el condensador es un componente eléctrico que almacena carga eléctrica, almacenando energía en un campo eléctrico.
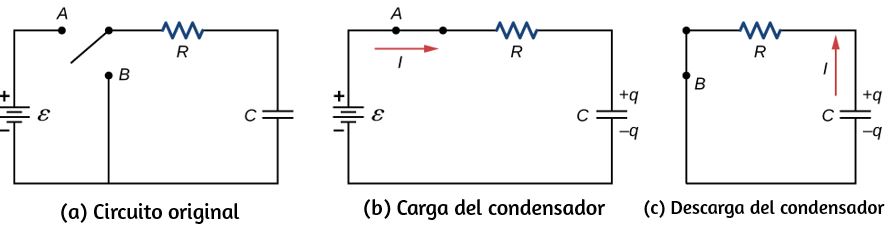
La (a) muestra un circuito RC simple que emplea una fuente de tensión cd (corriente continua) $ε$, un resistor $R$, un condensador $C$ y un interruptor de dos posiciones. El circuito permite que el condensador se cargue o descargue, dependiendo de la posición del interruptor. Cuando el interruptor se mueve a la posición $A$, el condensador se carga, lo que da como resultado el circuito en la parte (b). Cuando el interruptor se mueve a la posición $B$, el condensador se descarga a través del resistor.
Podemos usar la regla de ciclo de Kirchhoff para entender la carga del condensador. Esto da como resultado la ecuación $ε - V_R - V_C = 0$. Esta ecuación se puede usar para modelar la carga en función del tiempo a medida que se carga el capacitor. La capacitancia se define como $C = q/V$, por lo que la tensión en el capacitor es $V_C = q/C$. Usando la ley de Ohm, la caída de potencial a través de la resistencia es $V_R = IR$, y la corriente se define como $I = dq/dt$.
$$ε - V_R - V_C = 0,$$ $$ε - IR - \frac{q}{C} = 0,$$ $$ε - \frac{dq}{dt} - \frac{q}{C} = 0$$Esta ecuación diferencial se puede integrar para encontrar una ecuación para la carga en el condensador en función del tiempo.
$$ε - \frac{dq}{dt} - \frac{q}{C} = 0,$$ $$\frac{dq}{dt} = \frac{εC - q}{RC},$$ $$\int_0^q \frac{dq}{εC - q} = \frac{1}{RC}\int_0^t dt$$Dejando $u = εC - q$, entonces $du = -dq$. Obtenemos
$$-\int_0^q \frac{du}{u} = \frac{1}{RC}\int_0^t dt,$$Simplificando estos resultados en una ecuación para la carga en el condensador de carga como una función del tiempo:
En la (a) se muestra un gráfico de la carga en el condensador en función del tiempo. Primero ten en cuenta que a medida que el tiempo se acerca al infinito, la exponencial va a cero, por lo que la carga se aproxima a la carga máxima $Q = Cε$ y tiene unidades de culombios.
Las unidades de $RC$ son segundos, unidades de tiempo. Esta cantidad se conoce como la constante de tiempo:
En el momento $t = τ = RC$, la carga es igual a $1 - e^{-1} = 1 - 0.368 = 0.632$ de la carga máxima $Q = Cε$. Observa que el cambio de la tasa de tiempo de la carga es la pendiente en un punto de la gráfica de carga en función del tiempo. La pendiente del gráfico es grande en el tiempo $t = 0.0 s$ y se aproxima a cero a medida que aumenta el tiempo.
A medida que aumenta la carga en el condensador, la corriente a través de la resistencia disminuye, como se muestra en la (b).
La corriente a través de la resistencia se puede encontrar tomando la derivada de tiempo de la carga.
$$I(t) = \frac{dq}{dt} = \frac{d}{dt}[Cε(1 - e^{-t/RC})],$$ $$I(t) = Cε(\frac{1}{RC})e^{-t/RC} = \frac{ε}{R}e^{-t/RC} = I_0e^{-t/RC}$$En el tiempo $t = 0.00s$, la corriente a través del resistor es $I_0 = ε/R$. A medida que el tiempo se acerca al infinito, la corriente se acerca a cero. En el tiempo $t = τ$, la corriente a través de la resistencia es $I (t = τ) = I_0e^{-1} = 0.368I_0$.
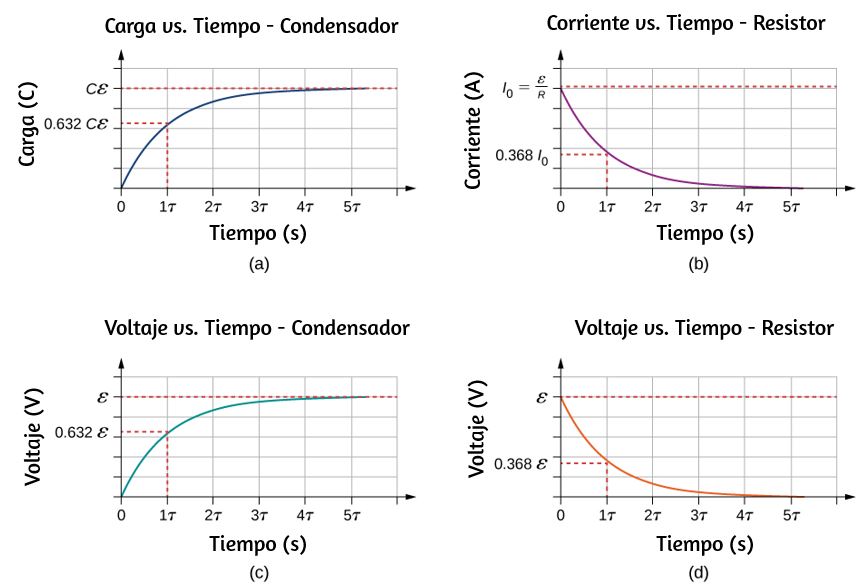
La (c) y la (d) muestran las diferencias de voltaje entre el condensador y el resistor, respectivamente. A medida que aumenta la carga en el condensador, la corriente disminuye, al igual que la diferencia de voltaje en el resistor $V_R(t) = (I_0R)e^{-t/τ} = εe^{-t/τ}$. La diferencia de voltaje en el condensador aumenta como $V_C(t) = ε(1 - e^{-t/τ})$.
Cuando el interruptor de la (a) se mueve a la posición $B$, el circuito se reduce al circuito en la parte (c) y el condensador cargado se puede descargar a través del resistor. En la (a) se muestra un gráfico de la carga del condensador en función del tiempo. El uso de la regla del ciclo de Kirchhoff para analizar el circuito a medida que el capacitor se descarga da como resultado la ecuación $-V_R - V_c = 0$, que se simplifica a $IR + q/C = 0$. Usando la definición de corriente $\frac{dq}{dt}R = -\frac{q}{C}qC$ e integrando la ecuación de ciclo, se obtiene una ecuación para la carga en el condensador en función del tiempo:
Aquí, $Q$ es la carga inicial en el condensador y $τ = RC$ es la constante de tiempo del circuito. Como se muestra en el gráfico, la carga disminuye exponencialmente desde la carga inicial, aproximándose a cero a medida que el tiempo se acerca al infinito. La corriente en función del tiempo se puede encontrar tomando la derivada de tiempo de la carga:
El signo negativo muestra que la corriente fluye en la dirección opuesta a la corriente encontrada cuando el condensador se está cargando. La (b) muestra un ejemplo de una gráfica de carga en función del tiempo y la corriente en función del tiempo.
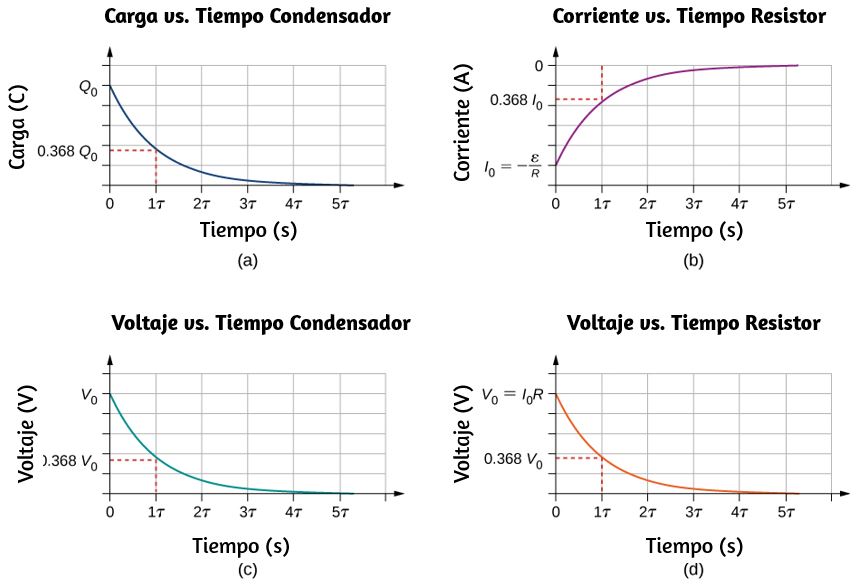
En las partes (c) y (d) de la figura se muestra un gráfico de la diferencia de voltaje a través del condensador y la diferencia de voltaje a través de la resistencia en función del tiempo. Ten en cuenta que las magnitudes de la carga, la corriente y el voltaje disminuyen exponencialmente, acercándose a cero a medida que aumenta el tiempo.
Ahora podemos explicar por qué la cámara de flash, mencionada al comienzo de esta sección, tarda mucho más en cargarse que en descargarse: la resistencia durante la carga es significativamente mayor que durante la descarga.
La resistencia interna de la batería representa la mayor parte de la resistencia durante la carga. A medida que la batería envejece, la resistencia interna creciente hace que el proceso de carga sea aún más lento.
La electricidad presenta dos peligros conocidos: térmico y de choque. Un riesgo térmico es aquel en el que una corriente eléctrica excesiva causa efectos térmicos no deseados, como iniciar un incendio en la pared de una casa. Se produce un riesgo de descarga eléctrica cuando una corriente eléctrica pasa a través de una persona. Los shocks varían en severidad desde letalidad dolorosa, pero inofensiva hasta letalidad que detiene el corazón. En esta sección, consideramos estos peligros y los diversos factores que los afectan de manera cuantitativa. También examinamos sistemas y dispositivos para prevenir riesgos eléctricos.
La energía eléctrica causa efectos de calentamiento no deseados cada vez que la energía eléctrica se convierte en energía térmica a un ritmo más rápido de lo que se puede disipar con seguridad.
Un ejemplo clásico de esto es el cortocircuito, una ruta de baja resistencia entre terminales de una fuente de voltaje.
Un ejemplo de un cortocircuito se muestra en la . Una tostadora está enchufada en una toma de corriente doméstica común. El aislamiento de los cables que conducen a un electrodoméstico se ha desgastado, permitiendo que los dos cables entren en contacto, o "cortocircuito". Como resultado, la energía térmica puede elevar rápidamente la temperatura de los materiales circundantes, derritiendo el aislamiento y quizás causando un incendio.
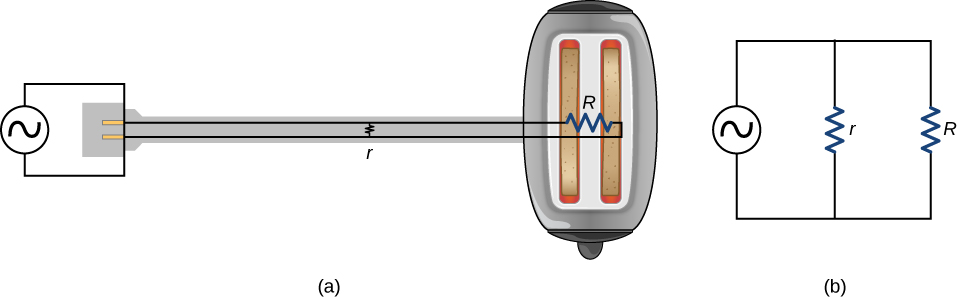
El diagrama del circuito muestra un símbolo que consiste en una onda sinusoidal encerrada en un círculo. Este símbolo representa una fuente de tensión de corriente alterna (CA). En una fuente de voltaje de CA, la tensión oscila entre una amplitud máxima positiva y una negativa.
Hasta ahora, hemos estado considerando fuentes de voltaje de corriente continua (CD), pero muchos de los mismos conceptos son aplicables a los circuitos de CA.
Otro peligro térmico grave ocurre cuando los cables que suministran energía a un artefacto están sobrecargados. Los cables y electrodomésticos a menudo se clasifican para la corriente máxima que pueden manejar con seguridad. El término "sobrecargado" se refiere a una condición donde la corriente excede la corriente máxima nominal. A medida que la corriente fluye a través de un cable, la potencia disipada en los cables de suministro es $P = I^2R_W$, donde $R_W$ es la resistencia de los cables y $I$ es la corriente que fluye a través de los cables. Si $I$ o $R_W$ son demasiado grandes, los cables se sobrecalientan. Los fusibles y los interruptores automáticos se usan para limitar las corrientes excesivas.
La descarga eléctrica es la reacción fisiológica o lesión causada por una corriente eléctrica externa que pasa a través del cuerpo. El efecto de una descarga eléctrica puede ser negativo o positivo. Cuando una corriente con una magnitud superior a $300 mA$ pasa a través del corazón, puede ocurrir la muerte. La mayoría de las muertes por descargas eléctricas ocurren porque una corriente causa fibrilación ventricular, un latido del corazón masivamente irregular y con frecuencia fatal. Por otro lado, una víctima de ataque cardíaco, cuyo corazón está en fibrilación, puede salvarse mediante una descarga eléctrica de un desfibrilador.
Los efectos de una descarga eléctrica indeseable pueden variar en gravedad: una ligera sensación en el punto de contacto, dolor, pérdida de control muscular voluntario, dificultad para respirar, fibrilación cardíaca y posiblemente la muerte.
La pérdida del control muscular voluntario puede hacer que la víctima no pueda soltar la fuente de la corriente.
Los principales factores de los que depende la gravedad de los efectos de la descarga eléctrica son
Nuestros cuerpos son conductores eléctricos relativamente buenos debido al contenido de agua del cuerpo. Una condición peligrosa ocurre cuando el cuerpo está en contacto con una fuente de voltaje y "tierra". El término "tierra" se refiere a un gran sumidero o fuente de electrones, por ejemplo, la tierra (por lo tanto, el nombre).
Cuando hay un camino directo a tierra, grandes corrientes pasarán a través de las partes del cuerpo con la resistencia más baja y un camino directo a tierra. Una precaución de seguridad utilizada por muchas profesiones es el uso de zapatos con aislamiento. Los zapatos con aislamiento prohíben un camino a tierra para los electrones a través de los pies al proporcionar una gran resistencia. Siempre que trabajes con herramientas de alta potencia o cualquier circuito eléctrico, asegúrate de no proporcionar una ruta para el flujo de corriente (especialmente a través del corazón). Una precaución de seguridad común es trabajar con una mano, reduciendo la posibilidad de proporcionar una ruta actual a través del corazón.
Las corrientes muy pequeñas pasan inofensivamente y no se sienten a través del cuerpo. Esto te sucede regularmente sin tu conocimiento. El umbral de sensación es de solo $1 mA$ y, aunque desagradable, los choques son aparentemente inofensivos para las corrientes de menos de $5 mA$.
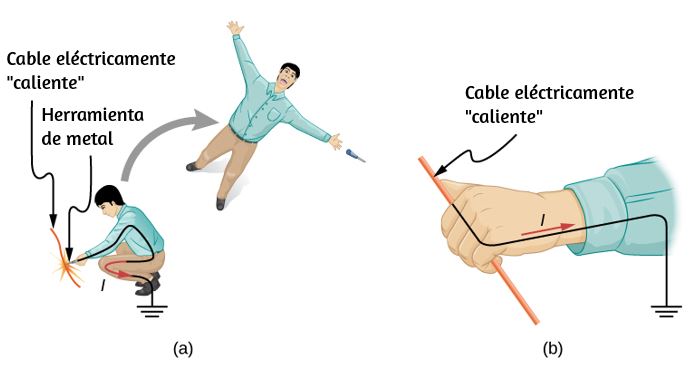
Un gran número de reglas de seguridad toman el valor de $5 mA$ para la descarga máxima permitida. A $5 - 30 mA$ y más, la corriente puede estimular contracciones musculares sostenidas, de forma similar a los impulsos nerviosos regulares (). Las corrientes muy grandes (más de $300 mA$) hacen que el corazón y el diafragma del pulmón se contraigan durante la duración del choque. Tanto el corazón como la respiración se detienen. Ambos a menudo vuelven a la normalidad después del shock.
La corriente es el principal factor que determina la severidad del choque. Un voltaje mayor es más peligroso, pero como $I = V/R$, la gravedad del choque depende de la combinación de voltaje y resistencia. Por ejemplo, una persona con piel seca tiene una resistencia de aproximadamente $200 kΩ$. Si entra en contacto con $120 V$ AC, una corriente
$$I = (120 V)/(200 kΩ) = 0,6 mA$$pasa inofensivamente a través de él. La misma persona empapada puede tener una resistencia de $10.0 kΩ$ y lo mismos $120 V$ producirán una corriente de $12 mA$, por encima del umbral de "no se puede soltar" y es potencialmente peligrosa.
La (a) muestra el esquema para un circuito simple de CA sin características de seguridad. Esta no es la forma en que se distribuye la potencia en la práctica. El cableado doméstico e industrial moderno requiere el sistema de tres cables, que se muestra esquemáticamente en la parte (b), que tiene varias características de seguridad, con cables en vivo, neutros y de tierra. Primero está el interruptor de circuito familiar (o fusible) para evitar la sobrecarga térmica. La segunda es una funda protectora alrededor del aparato, como una tostadora o un refrigerador.
La característica de seguridad de la carcasa es que evita que una persona toque los cables expuestos y entre en contacto eléctrico con el circuito, lo que ayuda a prevenir los shocks.
Hay tres conexiones a tierra que se muestran en la (b). Recuerda que una conexión a tierra es una ruta de baja resistencia directamente a tierra.
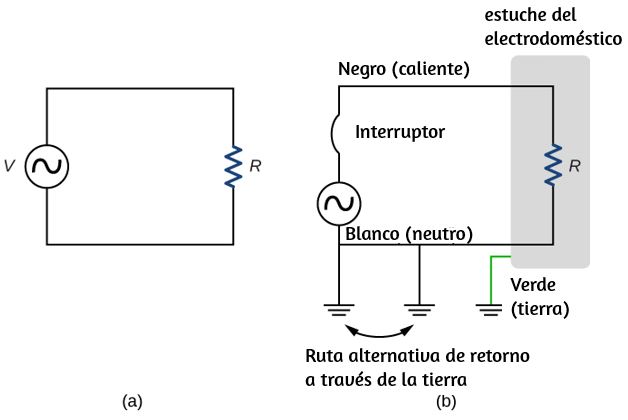
Las dos conexiones a tierra en el cable neutro lo obligan a estar a cero voltios con respecto a la tierra, dando el nombre al cable. Por lo tanto, este cable es seguro de tocar incluso si falta su aislamiento, generalmente blanco. El cable neutro es la ruta de retorno de la corriente a seguir para completar el circuito.
Además, las dos conexiones a tierra proporcionan un camino alternativo a través del suelo (un buen conductor) para completar el circuito. La conexión a tierra más cercana a la fuente de alimentación podría estar en la planta de generación, mientras que la otra está en la ubicación del usuario. El tercer motivo es para el caso del electrodoméstico, a través del cable de tierra verde, forzando también a que la caja esté a cero voltios. El cable activo o caliente (en lo sucesivo, "vivo/caliente") suministra tensión y corriente para operar el aparato. La muestra una versión más pictórica de cómo el sistema de tres hilos está conectado a través de un enchufe de tres patas a un dispositivo.
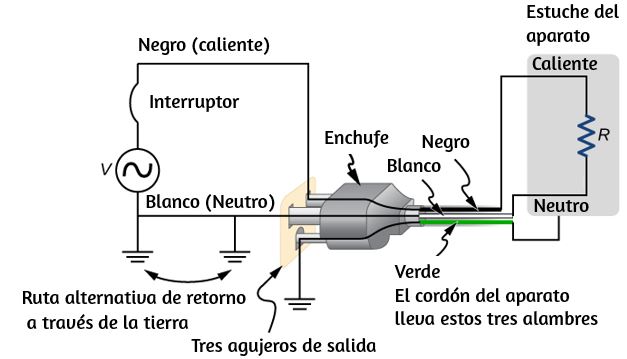
El plástico aislante está codificado por colores para identificar cables en vivo/caliente, neutros y de tierra, pero estos códigos varían en todo el mundo. Es esencial determinar el código de color en tu región. Los revestimientos rayados a veces se usan para el beneficio de aquellos que son daltónicos.
La conexión a tierra del caso resuelve más de un problema. El problema más simple es el aislamiento desgastado en el cable vivo/caliente que le permite contactar la carcasa, como se muestra en la . Al carecer de una conexión a tierra, es posible un choque severo. Esto es particularmente peligroso en la cocina, donde hay una buena conexión a tierra disponible a través del agua en el piso o un grifo de agua. Con la conexión a tierra intacta, el interruptor se disparará, forzando la reparación del aparato.
Un interruptor de circuito de falla a tierra (GFCI) es un dispositivo de seguridad que se encuentra en el cableado de la cocina y el baño, que funciona según la inducción electromagnética. Los GFCI comparan las corrientes en los cables vivo/caliente y neutro. Cuando las corrientes en vivo/caliente y neutral no son iguales, es casi siempre porque la corriente en el neutro es menor que en el cable vivo/caliente. Entonces parte de la corriente, llamada corriente de fuga, está regresando a la fuente de voltaje por una ruta que no sea a través del cable neutro. Se supone que este camino presenta un peligro. Los GFCI suelen configurarse para interrumpir el circuito si la corriente de fuga es superior a $5 mA$, la descarga inofensiva máxima aceptada. Incluso si la corriente de fuga pasa a tierra de manera segura a través de un cable de tierra intacto, el GFCI se disparará, forzando la reparación de la fuga.