Unidad 5.2
Superficies de revolución
Referencia curricular
Propósito
Anticipar las características de los cuerpos que se generan al girar o trasladar figuras. Construir desarrollos planos de conos y cilindros rectos. Anticipar y reconocer las secciones que se obtienen al realizar cortes a un cilindro o a un cono recto. Determinar la variación que se da en el radio de los diversos círculos que se obtienen al hacer cortes paralelos en una esfera o cono recto.
Instrucciones generales
La unidad se divide en tres apartados:
- Superficies de revolución.
- Torno.
- Secciones cónicas .
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
![]()
|
1. Superficies de revolución
En este apartado se pretende familiarizar a los alumnos con las superficies de revolución y con cómo se generan a partir de una línea que se hace girar sobre su propio eje.
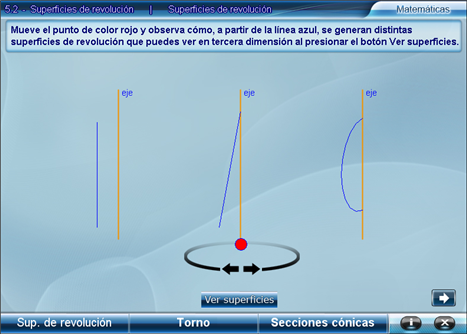
El alumno debe mover en forma circular el punto rojo para iniciar el trazado de las tres superficies de revolución mostradas: cilindro, cono hueco y esfera hueca.

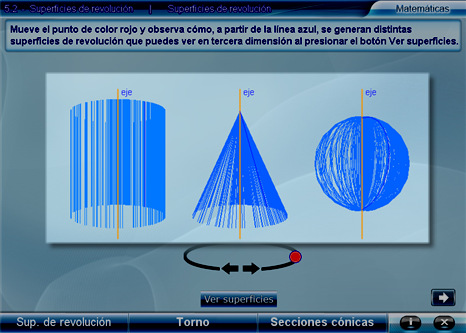
Con el botón Ver superficies se visualizan las superficies generadas y con el botón izquierdo del ratón, se pueden mover y girar para observarlas desde diversas perspectivas. En este momento, aparece el botón Reiniciar por si se quiere revisar de nuevo el trazado de las superficies.
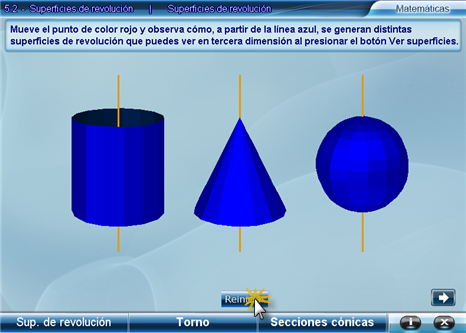
2. Torno
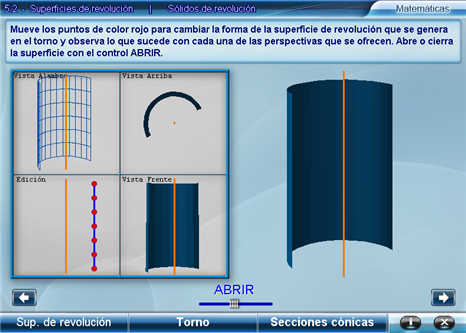
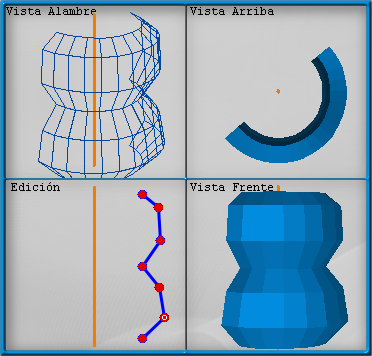
En este apartado el alumno manipula un conjunto de puntos que forman una línea o curva para que, al girarla sobre su propio eje, se genere una determinada superficie de revolución.
El usuario mueve los puntos con el ratón, y puede acercarlos, alejarlos y unirlos, de manera que se observarán las modificaciones a la superficie de revolución.
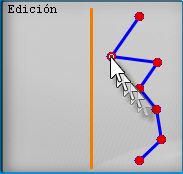

Además, con el control ABRIR se puede abrir o cerrar gradualmente la figura para ver la superficie en el interior.

Se muestran simultáneamente diferentes puntos de vista de la superficie.
En el siguiente apartado el alumno se familiarizará con el origen de cada una de las cónicas, para ello podrá manipular un plano cortando a un cono doble y observará qué variables intervienen en la formación de las superficies cónicas.
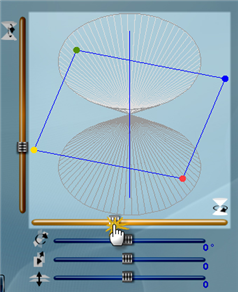
En la imagen se muestra la pantalla de entrada de este aparatado, en ella se observa un cono doble y un plano perpendicular a la pantalla, además hay un conjunto de controles que manipulan el ángulo de giro del cono tanto en el eje vertical como en el horizontal, el ángulo de giro del plano, su elevación (arriba, abajo) y su aproximación a la pantalla (frente, atrás).
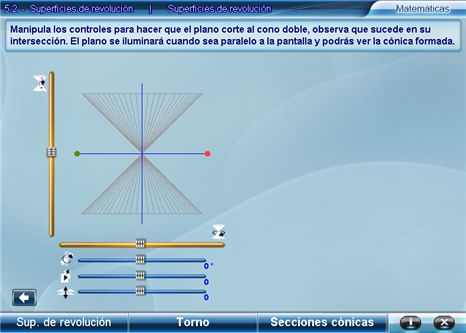
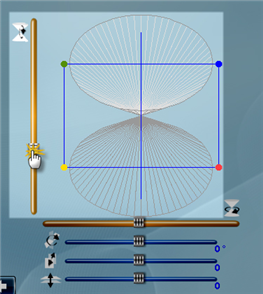
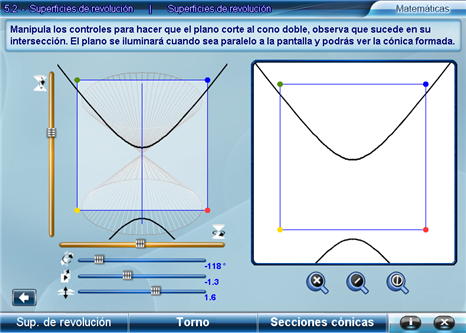
Al manipular los controles el alumno formará diferentes intersecciones del plano con el cono, en función de esta manipulación, la intersección formada será una circunferencia, una elipse, una parábola y una hipérbola respectivamente.

Para ver el plano paralelo a la pantalla se deben mover los controles de ángulo del cono, hasta que el plano se ilumine de color blanco, lo que es una señal de que el usuario está viendo el plano justo por encima y por consiguiente puede visualizar la cónica formada. Además, aparecerá un panel al lado derecho con la misma vista de frente al plano.
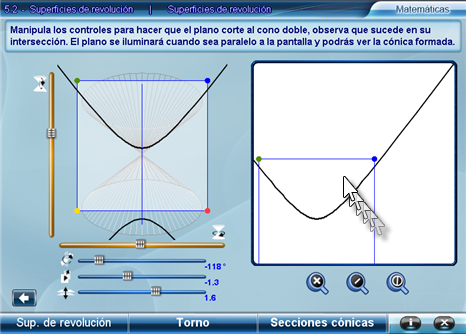
Debajo del panel derecho hay tres botones que sirven para acercar, alejar o centrar la vista del plano y la cónica, ponga mucha atención en los puntos que conforman el plano, pues corresponden entre sí, esto le ayudará a saber la orientación del plano. Puede manipular el panel derecho con el puntero del ratón, arrastrándolo sobre él se moverá el plano y la cónica.
Sugerencias didácticas
-
Lea las instrucciones en voz alta.
-
Antes de comenzar, podría preguntar a sus alumnos qué tipo de figura se generaría al rotar una línea recta como la que se muestra en la parte izquierda de la pantalla.
-
Haga algo similar con las otras dos curvas.
-
Permita que ellos manipulen el apartado y guíe un intercambio de opiniones sobre si se generaron las figuras esperadas o no.
-
En el segundo apartado, estimule a los estudiantes para estimar o predecir las figuras que se formarían usando cierto arreglo de puntos. Luego, hágalo al revés, proponga una figura y que ellos resuelvan el arreglo de puntos.
Créditos
Autor
Carlos Alberto Jaimes Vergara
Agradecimiento
A Deyanira Monroy Zariñán por su constante revisión y supervisión en el desarrollo de la unidad.
Reconocimientos
Los apartados Superficies de revolución y Secciones cónicas están basados en los recursos interactivos Superficies de revolución y Seccionando el cono respectivamente, desarrollados por Eduardo Barbero Corral de la Red Educativa Digital Descartes de España.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)

