Unidad 5.1
Ecuaciones y sistemas de ecuaciones
Referencia curricular
Propósito
Dado un problema, determinar la ecuación lineal, cuadrática o sistema de ecuaciones con que se puede resolver, y viceversa, proponer una situación que se modele con una de esas representaciones.
Instrucciones generales
La unidad consta de un apartado:
Este menú aparece a lo largo del interactivo y conserva su funcionalidad.

El botón |
 |
brinda acceso a la ayuda de las escenas interactivas. |
1. Modelación de problemas
Esta unidad presenta al alumno problemas que pueden modelarse con una ecuación líneal o cuadrática o con un sistema de ecuaciones lineales o uno con una ecuación lineal y una cuadrática. En todos los casos el procedimiento es el mismo.
En ambos problemas hay un botón con una interrogación ? que despliega una página en la que se ejemplifica el procedimieto a seguir para resolver un problema modelándolo matemáticamente. En el primer problema, el botón ? muestra el procedimiento ilustrándolo con el mismo problema de la escena. En el segundo problema la ilustración se hace con un problema diferente.
Durante el primer, problema se pide al usuario calcular el ancho del margen de un marco para una pintura. Se dan los datos del ancho y alto de la pintura y el área total que debe abarcar el margen. El programa va guiando al usuario paso a paso pidiéndole que:
- Reconozca los datos del problema.
- De nombre a la incógnita.
- Plantee la ecuación que servirá para resolver el problema.
- Estime la solución en forma gráfica.
- Obtenga la solución o soluciones exactas de la ecuación.
- Elija la solución de la ecuación que resuelve el problema.
- Compruebe que es solución de la ecuación.
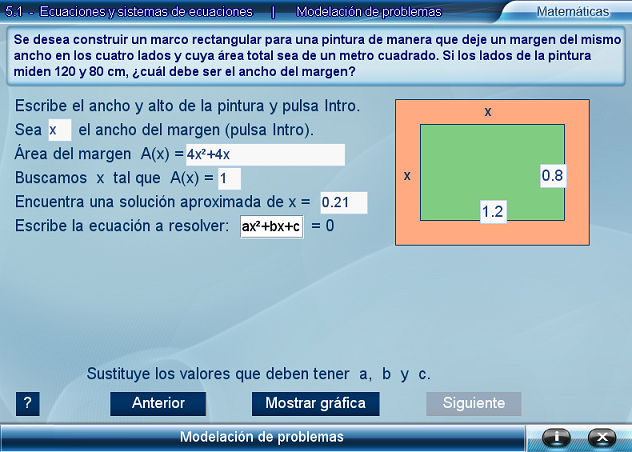
En cada paso (excepto el primero) el botón Siguiente aparece desactivado. El usuario debe responder algo usando para ello algún o algunos controles (campos de texto). Cuando la respuesta es correcta se activa el botón Siguiente y se desactivan los campos de texto que contienen las respuestas correctas.

Al terminar, el interactivo ofrece al usuario otro problema.
En el segundo problema se sigue un procedimiento ligeramente diferente al anterior, pero que en escencia es el mismo. Lo primero que se pide al usuario es graficar los puntos conocidos a partir de los datos del problema. En otras palabras, los datos de un problema se representan gráficamente. Luego se le pide al alumno encontrar el tipo de ecuación o sistema de ecuaciones adecuado para modelar el problema. Como ayuda para encontrar la ecuación o el sistema de ecuaciones, se ofrece la posibilidad de ajustar las rectas o parábolas de las ecuaciones a los datos del problema. En general, esto lleva a descubrir cuál es el planteamiento adecuado.
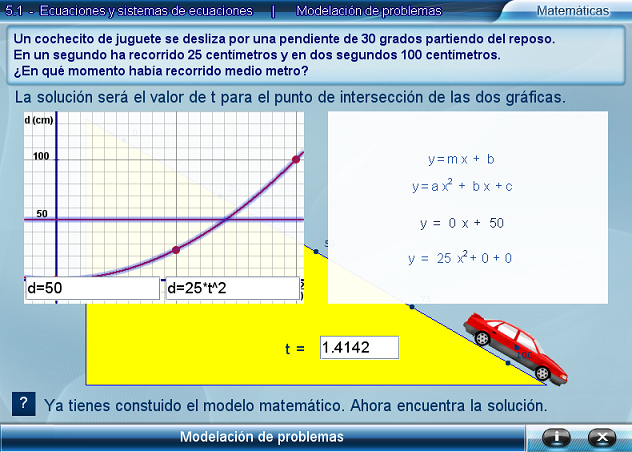
Ya que el estudiante encuentra el planteamiento correcto puede acceder al proceso de solución que lo guiará para encontrar la solución numérica al problema, siempre relacionándola con la gráfica. Por ejemplo, a veces el problema se resuelve encontrando la ordenada de un punto sobre una de las gráficas dada su abscisa, otras veces es la intersección de dos rectas o de una recta y una parábola.
Sugerencias didácticas
Es conveniente que se repase en clase el procedimiento de solución recomendado al que puede accederse pulsando el botón ?. Conviene dejar que los alumnos resuelvan el problema guiados por el interactivo. Si encuentran dificultades en un paso pueden consultar el botón ? o bien al maestro. Al terminar, es pertinente que el grupo analice qué tan general resulta el procedimiento recomendado y el por qué de cada paso. Finalmente, pueden explorar otros procedimientos que se propongan.
Una vez resueltos ambos ejercicios, se recomienda intercambiar opiniones sobre las semejanzas y diferencias entre los planteamientos y los métodos seguidos para resolverlos.
Conviene plantear a los alumnos
problemas similares y pedirles que los resuelvan, en su cuaderno,
usando un procedimiento parecido al sugerido en esta unidad.
Créditos
Autor
José Luis Abreu León
Colaboraciones
La unidad fue sugerida y parcialmente diseñada por Deyanira Monroy Zariñán.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
