Unidad 4.5
Análisis de datos
Referencia curricular
Propósito
Ilustrar que en ocasiones la información numérica detallada de un fenómeno puede esconder relaciones funcionales relativamente simples pero no triviales.
Instrucciones generales
La unidad consta de un apartado:
Este menú aparece a lo largo del interactivo y conserva su funcionalidad.

El botón |
 |
brinda acceso a la ayuda de las escenas interactivas. |
.
La tercera ley de Kepler
El alumno analizará un conjunto de datos sobre el Sistema solar que lo llevarán a encontrar una relación simple pero no evidente entre ellos y de esta manera descubrirá la tercera ley de Kepler. La unidad intenta mostrar al estudiante cómo fue que Johannes Kepler descubrió la tercera ley del movimiento planetario. Esto se logra graficando los datos numéricos y observando que un par de ellos, los radios de las órbitas y los Periodos de revolución, parecen guardar una relación que no es ni lineal ni cuadrática pero es cercana a ambas. Así fue como Kepler descubrió lo que se conoce como la tercera ley de Kepler: Los cuadrados de los periodos de revolución de los planetas alrededor del Sol son proporcionales a los cubos de los radios de sus órbitas.
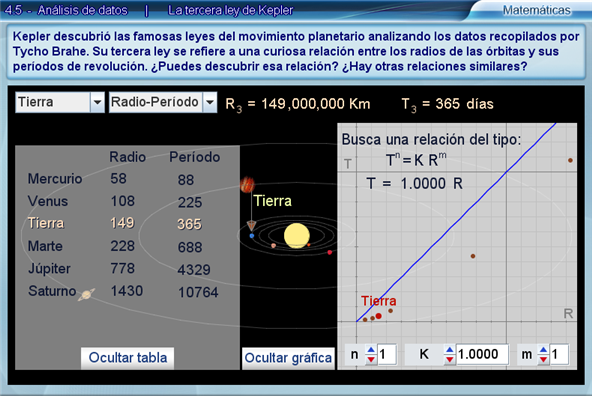
Al centro de la escena aparecen el Sol y los planetas que se conocían en la época de Kepler girando alrededor suyo. Por eso no aparecen Urano y Neptuno. La simulación permite reconocer visualmente los datos presentados pues está hecha con una proporción cercana a la realidad, aunque ligeramente modificada para que sea más fácilmente comprensible. La velocidad de la animación es tal que un año se reduce aproximadamente a medio minuto. Las masas de los planetas son aproximadamente proporcionales a los volúmenes de las esferas que los representan y los radios de las órbitas dibujadas son proporcionales a las raíces cuadradas de los radios de las órbitas reales. Esto último se hace porque si se tomaran proporcionales a los reales, quedarían tan separados unos de otros que no podrían visualizarse con comodidad.
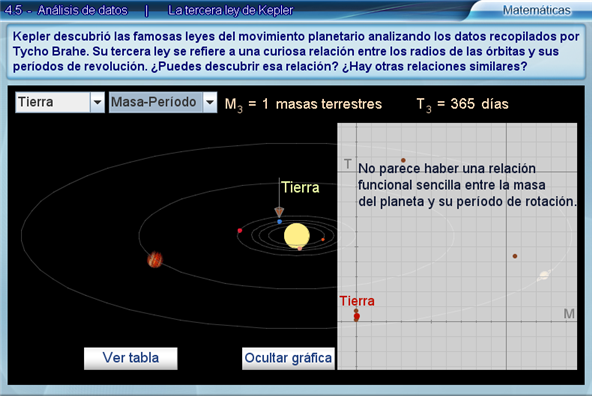
La escena presenta dos menús. El primero permite al alumno seleccionar un planeta y el segundo un par de variables (Radio-Periodo, Radio-Masa o Masa-Periodo). A la derecha de estos menús aparece la información correspondiente al planeta seleccionado. El alumno podrá ver que no hay una relación evidente entre las variables.
Abajo, aparecen dos botones que muestran una tabla con los valores del par de variables seleccionado para todos los planetas y, tambié, una gráfica con los puntos correspondientes dibujados en ella.
Sugerencias didácticas
Plantee al grupo que intente descubrir relaciones funcionales entre los datos presentados en las tablas. Los estudiantes podrían marcar los puntos en una gráfica de R contra T en su cuaderno y observar que hay una relación no lineal aparente, que más bien parece cuadrática, pero en realidad tampoco lo es.
Para profundizar en el problema conviene abrir la tabla. En la tabla correspondiente a la pareja "Radio-Masa", puede verse que a medida que los radios crecen, la masa no presenta un comportamiento de crecimiento ni decrecimiento. Por ejemplo, el radio de la órbita de Venus y su masa son menores que los de la Tierra; sin embargo, aunque el radio de la órbita de Marte es mayor que el de la Tierra, su masa es menor. Algo similar sucede entre Marte, Júpiter y Saturno, en los cuales los radios de sus órbitas crecen, pero la masa primero crece y luego disminuye. Algo similar ocurre en la tabla correspondiente a "Masa-Periodo".
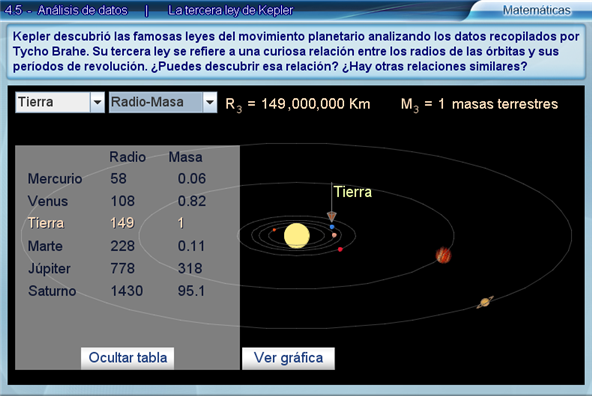
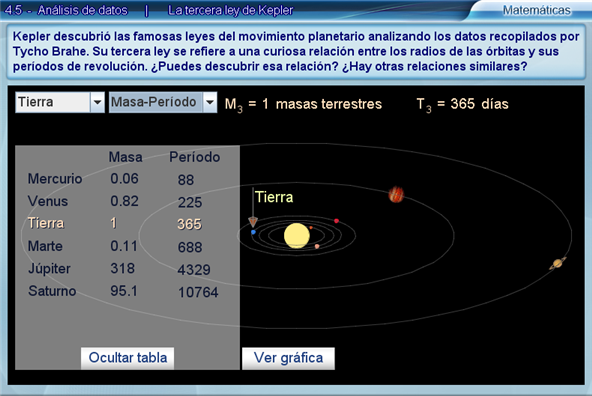
El único par de variables en el que se aprecia una relación directa y clara es Radio-Periodo el radio de las órbitas y los periodos de revolución. Pero esta relación no es de proporcionalidad directa, como podría creerse a primera vista. Se sugiere pedir a los alumnos que busquen, trabajando en sus cuadernos, una constante de proporcionalidad y comprueben que tal cosa no existe. Entonces es el momento de plantear claramente la siguiente pregunta: ¿Qué tipo de relación hay entre los radios de las órbitas y los periodos de revolución?
Para responder a ella, hay que abrir la gráfica correspondiente y trabajar un poco. Al presionar Ver gráfica se abre una ventana con un plano cartesiano en el que están dibujados en color rojo los puntos que corresponden al par de variables seleccionado. Las gráficas de Radio-Masa y de Masa-Periodo muestran los puntos distribuidos de manera que no reflejan una relación entre ellos.
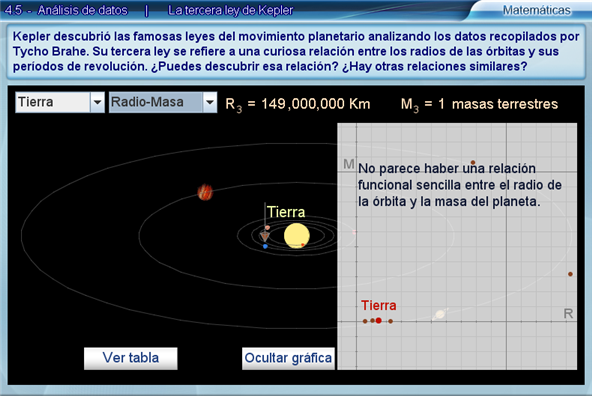
Sin embargo la gráfica de Radio-Periodo muestra los puntos alineados a lo largo de una curva. En la gráfica aparece una ecuación, una línea azul que representa la relación entre los radios y las órbitas de los planetas según la ecuación planteada y unos controles numéricos. La ecuación es una relación entre el periodo T y el radio R, de la forma Tn = k Rm. El estudiante deberá encontrar los valores de k, m y n que hacen que la gráfica de dicha ecuación pase por todos los puntos dibujados y que corresponden a los datos de los planetas.
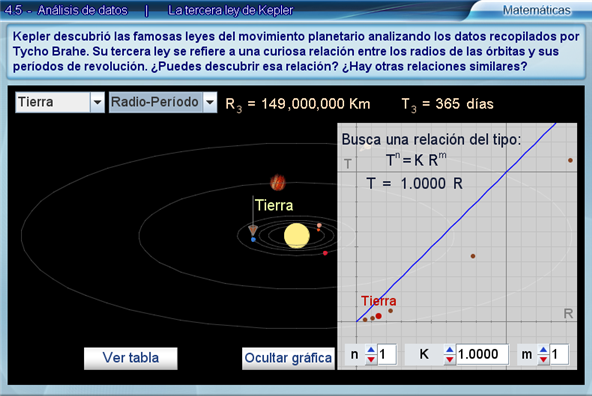
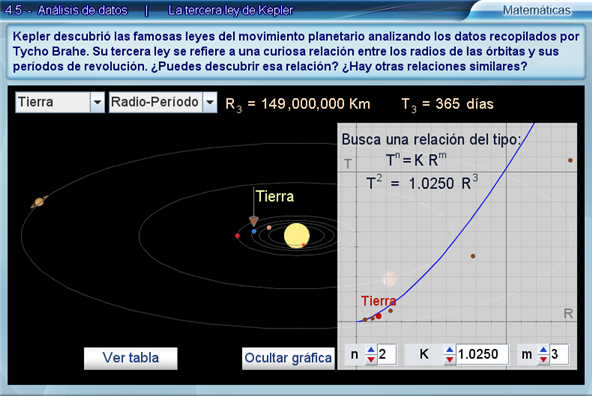
Con n=1 y m=1 la gráfica azul es una recta que no puede hacerse pasar por todos los puntos rojos. Con n=2 y m=1 la gráfica es una parábola con curvatura opuesta a la de la curva buscada. Con n=1 y m=2 la gráfica es una parábola con curvatura similar a la curva que buscamos, pero al variar k podrá verse que no puede pasar por todos los puntos rojos. Con n=2 y m=2 la gráfica vuelve a ser una recta. Finalmente con n=2 y m=3 la gráfica tiene el aspecto deseado y, modificando el valor de k, puede encontrarse uno que hace pasar la gráfica por todos los puntos rojos. Al llegar a este punto el estudiante habrá descubierto la tercera ley de Kepler: T2= k R3.
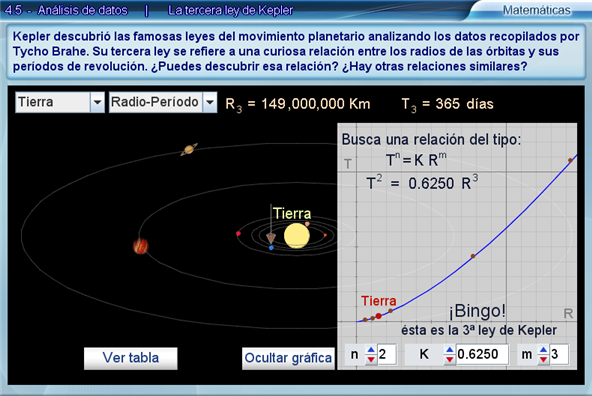
El valor específico de k es una constante de la naturaleza que está relacionada con la fuerza de atracción que, según la ley de la gravitación universal, ejerce un cuerpo sobre otro. Pero esto corresponde ya a otra época, a otro genio de la física y las matemáticas: Isaac Newton, y a la explicación que dio de las leyes de Kepler a partir de las leyes más fundamentales del movimiento de los cuerpos.
Créditos
Autor
José Luis Abreu León
Colaboraciones
La unidad fue sugerida y parcialmente diseñada por Deyanira Monroy Zariñán.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
