Unidad 4.4
Crecimiento exponencial
Referencia curricular
Propósito
Interpretar y comparar las representaciones gráficas de crecimiento aritmético o lineal y geométrico o exponencial de diversas situaciones.
Instrucciones generales
La unidad se divide en tres apartados:
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo del interactivo y conserva su funcionalidad.
El botón |
 |
brinda acceso a la ayuda de las escenas interactivas. |
Se puede navegar entre las escenas con las flechas que hay en la parte inferior de las mismas.
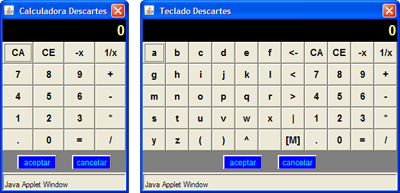
Uso de calculadora
Al hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.
En ambos casos, al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá en el campo de texto o en la celda el último resultado escrito en ella.
Cuando se escribe una expresión numérica como 2^3+4 (el símbolo "^" se utiliza para elevar a una potencia determinada: 2^3 +4 = 23+4), al presionar Aceptar lo que aparecerá será el resultado de la operación, en este caso 12.
Uso de campos de texto
En algunas escenas aparecen campos de texto donde el usuario escribe valores,
expresiones numéricas o algebraicas. Al terminar, en la mayoría
de los casos, se oprime la tecla Intro o un botón con el
símbolo 
. Sin embargo, hay ocasiones en que
basta con apretar el botón Verificar o mover el cursor
hacia otro campo de texto. Los usos particulares se detallan en la escena o
el apartado correspondiente.
1. Ajedrez
En esta unidad se interpretan y comparan distintas gráficas de crecimiento aritmético o lineal y geométrico o exponencial para una situación dada: una leyenda sobre el origen del ajedrez.
Al iniciar la escena se muestra brevemente una de las leyendas de la invención del ajedrez,
en forma de diapositivas.
Se puede avanzar o retroceder en la historia con los botones 
,
respectivamente.
Después de leer con atención la leyenda sobre el origen del ajedrez, el alumno debe analizar las tres reglas planteadas e inferir su comportamiento. Luego tiene que elegir aquella que daría mayor número de granos al inventor.
Para seleccionar una opción el alumno tiene que ponerla al frente de las demás
utilizando los botones 
,
y después presionando Aceptar del lado derecho de la escena.
Dependiendo de la respuesta seleccionada, se despliega un letrero de correcto o incorrecto. En cualquiera de los dos casos, a modo de retroalimentación se pide al alumno que incremente el valor del pulsador que corresponde al índice de la casilla del tablero en la cual se calcula la cantidad de granos.
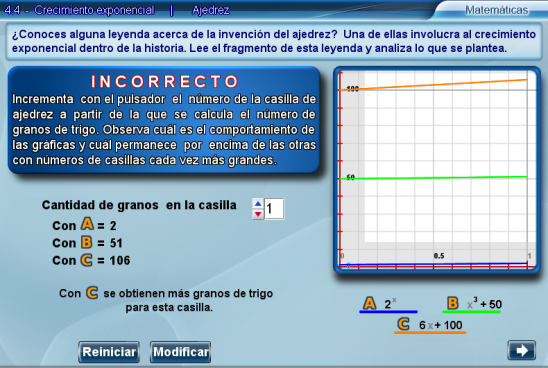
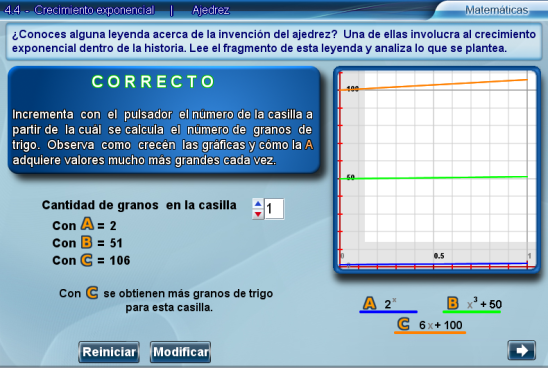
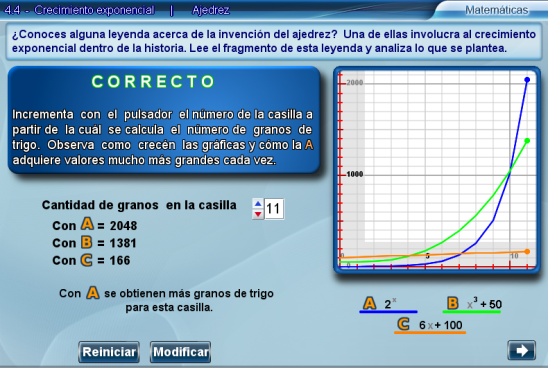
En este punto el alumno debe observar que al principio las gráficas resultantes de las ecuaciones correspondientes a las opciones B y C están por encima de la ecuación A, pero al ir incrementando el valor del pulsador, esto se invierte. Además, para valores relativamente pequeños como el 11 en nuestro ejemplo, el valor en B y C es mucho menor que el de A.
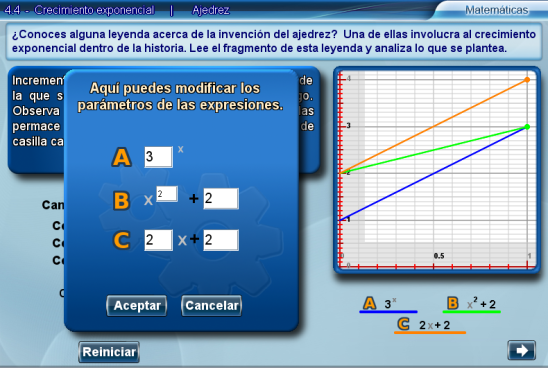
Por último, se pueden configurar los parámetros de cada una de las ecuaciones al presionar Modificar y realizar el mismo análisis que en el caso predeterminado.
Sugerencias didácticas
- Lea el texto de la leyenda en voz alta y permita que los estudiantes viertan sus opiniones antes de seleccionar una de las reglas.
- Permita que sean ellos quienes elijan la regla que aplicarían siempre y cuando justifiquen su respuesta.
- Compare con ellos las gráficas de las tres reglas.
- Se sugiere ir aumentando el número en el pulsador y analizar el comportamiento de las gráficas.
2. Decaimiento radioactivo
Esta escena pretende ejemplificar el comportamiento del decrecimiento exponencial a través de la simulación del decaimiento radiactivo de varios isótopos radioactivos. El decaimiento radioactivo es un proceso estadístico. Esto significa que si aisláramos a un átomo de material radioactivo, no sabríamos en qué momento decaería. En cambio, si consideramos unos 1000 átomos de C14 tenemos que en un periodo de 5730 años es muy probable que la mitad de estos átomos hayan decaído. En los siguientes 5730 años, habrán decaído la mitad de los átomos restantes y así sucesivamente en forma exponencial. A este periodo en el cual decae la mitad de los átomos, se le denomina periodo de semidesintegración y es un valor característico de cada núcleo.
Entonces:
| N | = | N0 |
| 2λt |
Donde:
| N0 | = | Número inicial de partículas | ||
| T½ | = | Periodo de semidesintegración |
||
| λ | = |
|
||
| t | = | El periodo de tiempo transcurrido | ||
| N | = | Número de partículas restantes al |
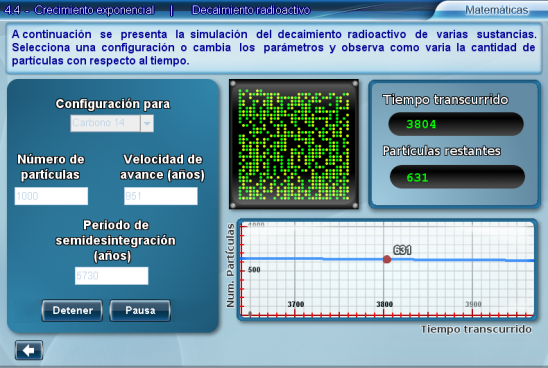
A continuación se listan los componentes de la escena:
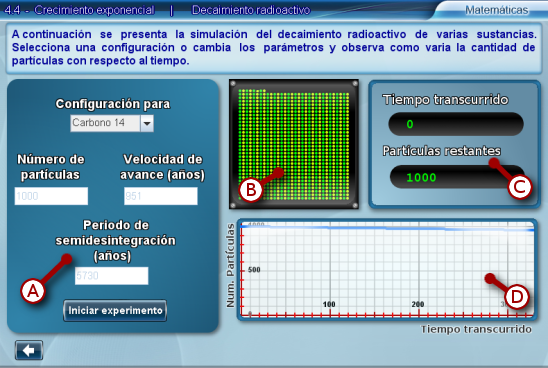
- A) Panel de datos y selección de la sustancia
- Aquí se puede seleccionar una de las siguientes sustancias para hacer la simulación: Carbono 14, Cobalto 60, Radio 226, Bismuto 207 o Estroncio 90. Además, una vez seleccionada, se muestran ciertas caraterísticas suyas relevantes para la simulación. En este panel también se puede seleccionar el número inicial de partículas de la sustancia y cuantos años equivalen a cada iteración en la simulación, es decir, cada cuantos años se tomará la lectura de cuantas partículas quedan.
- B) Contenedor de partículas
- Simula que contiene partículas de la sustancia seleccionada. A medida que avance el tiempo de la simulación, irán desapareciendo por el decaimiento.
- C) Datos del experimento
- Muestra la cantidad de partículas que quedan y el tiempo transcurrido.
- D) Gráfica
- En este panel se grafican los resultados de la simulación. El eje x corresponde al tiempo transcurrido y el eje y a las partículas restantes.
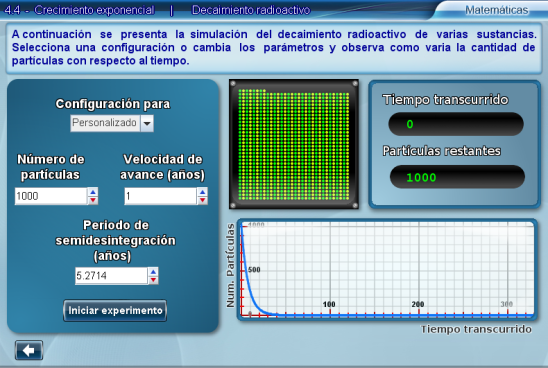
Por último, si se desea, se puede personalizar el experimento. Al seleccionar Personalizado del menú de configuraciones, la escena permitirá modificar el periodo de semidesintegración.
Sugerencias didácticas
-
Haga notar que a pesar de que en un principio la cantidad de partículas decrece muy
rápido (como con el cobalto), llega un momento en el que dejan de disminuir y
es cuando sólo queda una. Esta es una de las características principales del
decrecimiento exponencial, que es asintótico a en eje X o que nunca toma
el valor de 0. Sin embargo, tanto en la simulación como en la realidad, toma el valor de cero después de un tiempo
relativamente enorme con respecto al tiempo total.
-
Proponga a los alumnos la siguiente actividad. Recorte una hoja de papel en dos mitades
y descarte una de ellas. Repita la operación con la mitad que se quedó hasta que ya no
sea posible recortar a la mitad de nuevo. Haga preguntas a los alumnos para que infieran lo siguiente.
- La diferencia entre el área de la mitad creada el paso anterior con respecto a la mitad actual es cada vez menos evidente.
- Aunque se pudiera seguir cortando, si se sigue descartando la mitad, siempre se quedarán con una parte de la hoja (El área nunca se hace 0).
Créditos
Autor
Oscar Escamilla González
Colaboraciones
La unidad fue desarrollada con los lineamientos y asesoría didáctica y
pedagógica de Deyanira Monroy Zariñán y José Luis Abreu León.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de
La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)