Unidad 4.3TrigonometríaReferencia curricularPropósitoReconocer y determinar las razones trigonométricas, como cocientes entre las medidas de los lados, en familias de triángulos rectángulos semejantes. Calcular medidas de lados y de ángulos de triángulos rectángulos a partir de los valores de razones trigonométricas. Resolver problemas sencillos, en diversos ámbitos, utilizando las razones trigonométricas. Instrucciones generalesLa unidad se divide en cuatro apartados: 1. Explora Se puede navegar entre los
apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
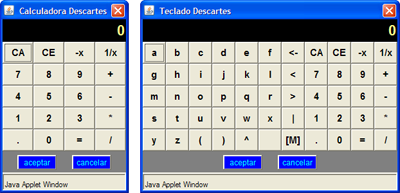
. Se puede navegar entre las escenas con las flechas que hay en la parte inferior de las mismas. Uso de calculadoraAl hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual. En ambos casos, al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá en el campo de texto o en la celda el último resultado escrito en ella. Cuando se escribe una expresión numérica como 2^3+4 (el símbolo "^" se utiliza para elevar a una potencia determinada: 2^3 +4 = 23+4), al presionar Aceptar lo que aparecerá será el resultado de la operación, en este caso 12.
Uso de campos de textoEn algunas escenas aparecen campos de texto donde el usuario escribe valores,
expresiones numéricas o algebraicas. Al terminar, en la mayoría de los casos, se oprime la tecla Intro o un botón con el símbolo Explora 1La escena tiene como finalidad familiarizar al alumno con algunas nomenclaturas y definiciones básicas del triángulo rectángulo, como la hipotenusa, el cateto adyacente y el cateto opuesto a un ángulo dado.Al inicio se presenta un triángulo rectángulo en posición arbitraria con los vértices y lados identificados respectivamente mediante literales mayúsculas y minúsculas.
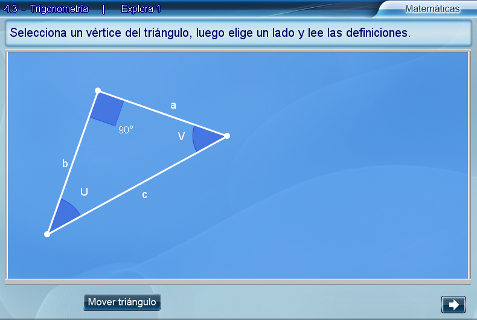
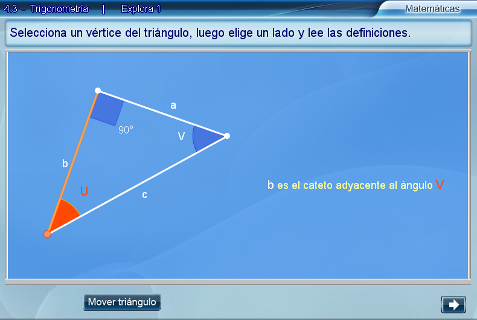
Cuando el estudiante selecciona vértices y luego, aristas del triángulo, se
generan las distintas definiciones que vinculan los elementos
seleccionados.
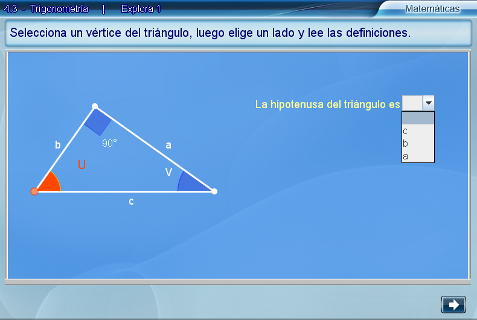
Al presionar Hacer ejercicios se pide al alumno que identifique la hipotenusa, el cateto adyacente y el opuesto a un ángulo dado, al elegir la respuesta del menú correspondiente.
Explora 2La siguiente escena tiene como finalidad definir seno, coseno y tangente. Cuando se elige cualquiera de los vértices, el interactivo muestra la función trigonométrica correspondiente.
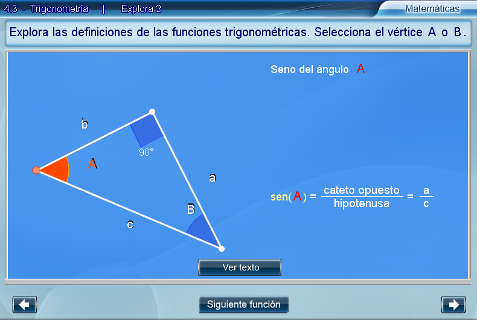
El botón Ver texto despliega un complemento de la definición, mientras que Siguiente función muestra las otras razones trigonométricas.
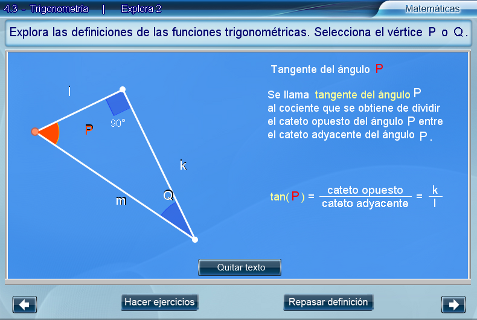
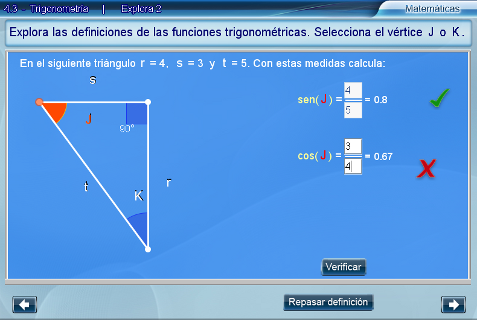
Al seleccionar Hacer ejercicios, el alumno escribe en los campos de texto los valores numéricos correspondientes. Con Repasar definición se reinicia la escena en cualquier momento. Si desea seguir practicando, puede oprimir Nuevo ejercicio.
Sugerencias didácticasProcure que sus alumnos realicen varios ejercicios antes de pasar al siguiente apartado. 2. ReconoceEste apartado consta de una escena. Reconoce
La siguiente escena inicia cuando se pide
al estudiante que reconozca al triángulo rectángulo que forma parte de
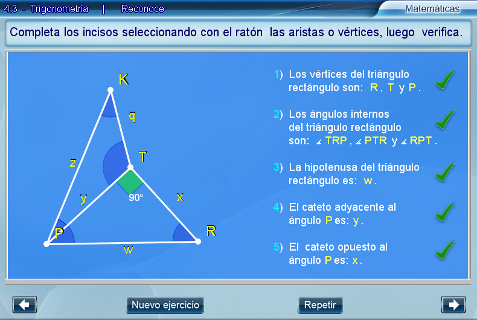
una figura compuesta por dos o más triángulos. El estudiante debe seleccionar los vértices del triángulo que considera rectángulo. Cuando su selección es correcta, tendrá que elegir las aristas y el vértice que correspondan a cada uno de los ángulos internos del triángulo rectángulo. A continuación, deberá señalar la hipotenusa y los catetos adyacente y opuesto. Para avanzar en cada uno de estos pasos se aprieta Verificar. Al término se puede oprimir Repetir o Nuevo ejercicio.
Sugerencias didácticasSe recomienda realizar tantos ejercicios como sean necesarios necesarios para reforzar los conceptos estudiados. 3. Tablas y círculo trigonométricoEste apartado consta de una escena. TablaEsta escena tiene como objetivo explorar el comportamiento de las funciones trigonométricas, cuando el ángulo sobre el cual se están evaluando varía de 0° a 90° de manera continua. Para ello, se usa el círculo unitario trigonométrico donde se aprecia la variación continua del ángulo A al mantener constante la hipotenusa. Por lo tanto, el cociente de las funciones trigonométricas sólo depende del valor de los catetos. Al mover el punto B se generan los valores que derivan de evaluar las funciones trigonométricas en aquellos ángulos que sean múltiplos de cinco y que se encuentren comprendidos entre 0° y 90°.
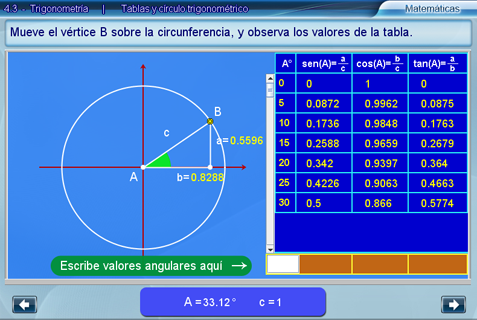
En la parte inferior de la tabla se puede escribir el valor de cualquier ángulo comprendido en el rango anterior y, al oprimir la tecla Intro, se obtienen las razones correspondientes.
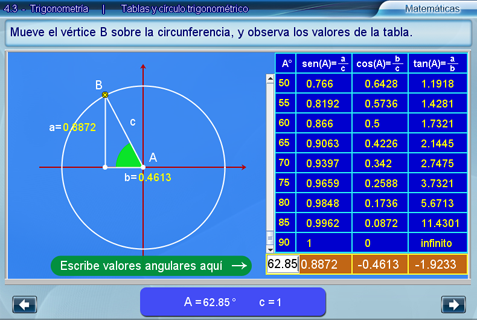
Sugerencias didácticasEs importante observar que para ciertos ángulos, los valores en la tabla podrían ser negativos. Esto siempre que las magnitudes consideradas al momento de sustituir los valores en los cocientes correspondientes, sean magnitudes dirigidas, es decir, con signo. Por ésta razón se podrían obtener valores negativos en la tabla; por ejemplo, si el ángulo se toma entre 90 y 180 grados, el cateto adyacente b siempre será negativo mientras que el cateto opuesto a será positivo. Luego, el seno y coseno de dicho ángulo resultarían negativos. Observación: Para evitar salirse del programa de estudios, la escena unicamente toma magnitudes absolutas, con la intención de no generar valores negativos para las funciones trigonométricas que se estudian. 4. ProblemasEste apartado consta de dos escenas donde el estudiante aplica las definiciones de las funciones trigonométricas estudiadas para solucionar problemas concretos. Por la similitud entre ambas, sólo se detalla la primera. 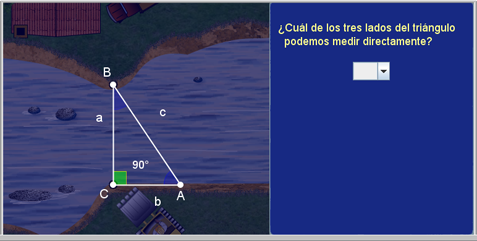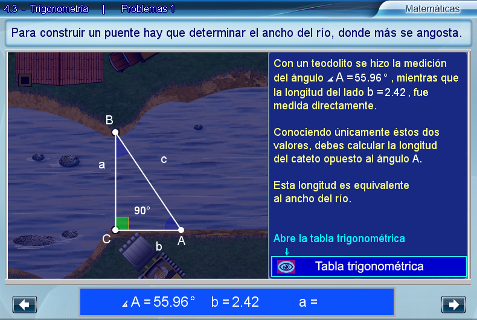Problemas 1En este caso se plantea la necesidad de construir un puente a lo ancho del río. A partir de ciertos datos iniciales -como la longitud que se mide sobre un lado del río y el ángulo recto que se forma- podrá recurrir a las funciones trigonométricas ya estudiadas para solucionar el problema. Para lo anterior, se pide que el alumno arrastre el triángulo sobre la imagen del río, de tal forma que sus vértices coincidan con las orillas. Es importante hacer notar que una de las posiciones adecuadas para resolver el problema es la que se muestra a continuación.
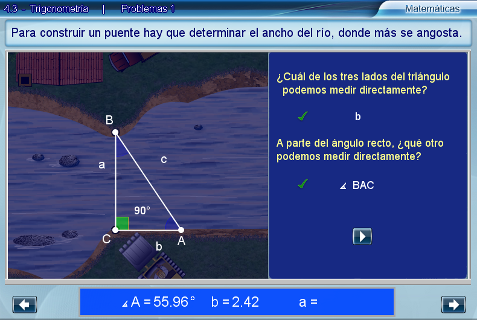
A continuación, aparecen dos preguntas que el estudiante debe responder
con opciones del menú. Mientras la respuesta no sea correcta, no
aparece el botón
Después de analizar la información, hay que desplegar la tabla trigonométrica mediante el botón
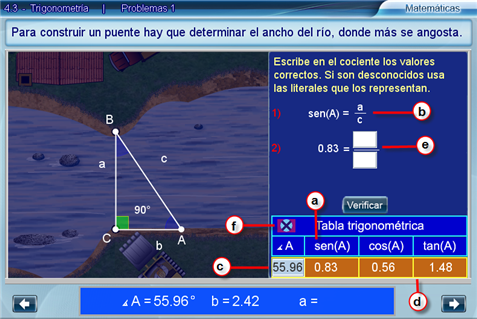
La siguiente lista explica los pasos a seguir. Cada vez que se sustituyan los valores o variables en una función trigonométrica se debe oprimir Verificar.
Cuando se encuentra el valor a que resuelve el problema, se muestra un campo de texto en el que se escribe la respuesta y se presiona Intro. Las medidas obtenidas pueden variar debido a que se está calculando una aproximación por el uso de sólo dos cifras decimales.
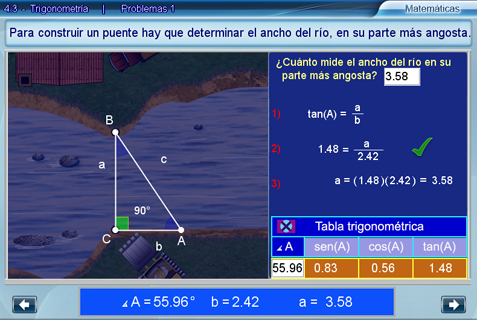
Se puede apretar Repetir para reiniciar el problema. Sugerencias didácticasEs importante recordar que la intención del apartado es poner en práctica las funciones trigonométricas. Si los alumnos no las manejan con soltura podría generar confusión. Se recomienda que resuelvan con el grupo el primer problemas y permita que, para el segundo, los estudiantes apliquen sin ayuda, sus conocimientos adquiridos. Créditos
Autor Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
.
Sin embargo, hay ocasiones en que basta con apretar el botón Verificar o mover el cursor hacia otro campo de texto. Los usos particulares se detallan en la escena o el apartado correspondiente.
para avanzar.
En la parte inferior de la escena hay un recuadro azul que contiene la incógnita y los datos conocidos del problema.
. Para ocultar, presionar el botón 
.
