Unidad 4.2
Teorema de Pitágoras
Referencia curricular
Propósito
Mostrar diferentes esquemas gráficos de demostraciones que facilitan la comprensión del Teorema de Pitágoras.
Resolver problemas aplicando el Teorema de Pitágoras.
Instrucciones generales
La unidad se divide en dos apartados:
- Aplicación
- Demostración
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.

El botón |
 |
brinda acceso a la ayuda de las escenas interactivas. |
Se puede navegar entre las escenas con las flechas que hay en la parte inferior de las mismas.
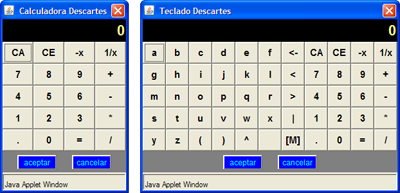
Uso de calculadora
Al hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.
En ambos casos, al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá en el campo de texto o en la celda el último resultado escrito en ella.
Cuando se escribe una expresión numérica como 2^3+4 (el símbolo "^" se utiliza para elevar a una potencia determinada: 2^3 +4 = 23+4), al presionar Aceptar lo que aparecerá será el resultado de la operación, en este caso 12.
Uso de campos de texto
En
algunas escenas aparecen campos de texto donde el usuario escribe
valores, expresiones numéricas o algebraicas. Al terminar, en la
mayoría de los casos, se oprime la tecla Intro o un botón con el símbolo  . Sin embargo, hay ocasiones en que basta con apretar el botón Verificar o mover el cursor hacia otro campo de texto. Los usos particulares se detallan en la escena o el apartado correspondiente.
. Sin embargo, hay ocasiones en que basta con apretar el botón Verificar o mover el cursor hacia otro campo de texto. Los usos particulares se detallan en la escena o el apartado correspondiente.
1. Aplicación
Este apartado tiene una escena. El objetivo es que el alumno utilice el Teorema de Pitágoras para resolver problemas prácticos.
Se plantea un problema que se puede esquematizar mediante un triángulo rectángulo del cual se conocen las medidas de dos de sus lados y donde la tercera medida corresponde a la respuesta del problema.
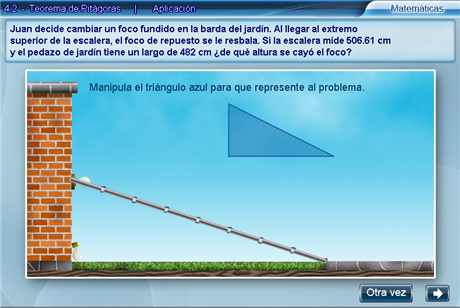
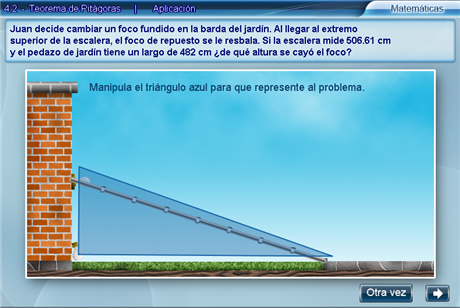
Primero, hay que arrastrar el triángulo azul por el vértice correspondiente al ángulo recto, hasta hacerlo coincidir con el ángulo recto formado por la pared y el césped. Después, hay que deformar el triángulo mediante sus vértices, correspondientes a los ángulos agudos, hasta hacerlo coincidir con el triángulo formado por la pared, el césped y la escalera.
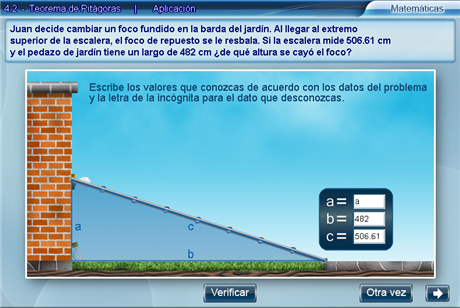
A continuación, hay que introducir los valores de las medidas de los lados a, b y c en las casillas correspondientes de la tabla; si no se conoce la medida, hay que introducir la letra en sí. Al terminar hay que presionar Verificar.
En lo sucesivo, hay que elegir de entre una lista de ecuaciones, aquella apropiada para encontrar el valor que hace falta y oprimir Verificar.
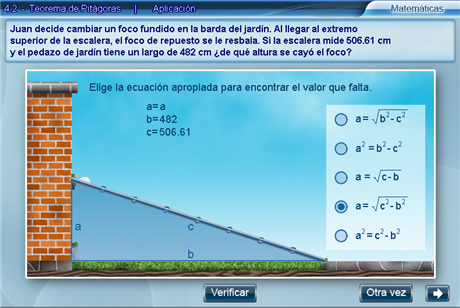
Luego, hay que sustituir los valores correspondientes en la ecuación -el valor buscado se indica con la misma letra- y presionar Verificar.
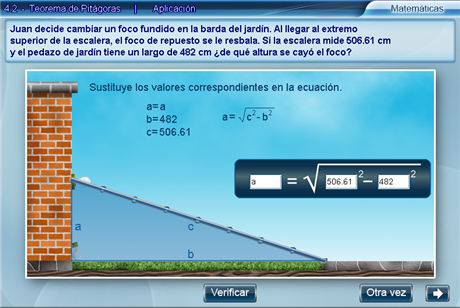
Enseguida, se deben introducir las soluciones de la ecuación en las casillas correspondientes de la tabla y apretar Verificar.
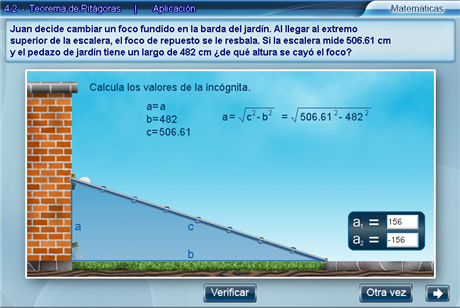
Por último, hay que responder la pregunta planteada en el problema, con base en las soluciones obtenidas, al introducir el valor correspondiente en la casilla y verificarlo.
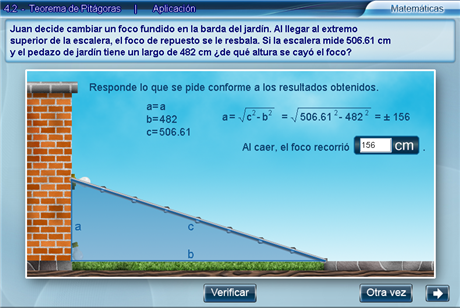
Para resolver un ejercicio distinto hay que oprimir Otra vez.
Sugerencias didácticas
- En cada paso lea las instrucciones en voz alta y cerciórese de que quede claro el objetivo buscado.
- Permita que los alumnos completen cada paso en el pizarrón. Pueden formar equipos para que resuelvan sendos ejercicios.
- Resuelvan varios ejercicios hasta que quede clara la forma de utilizar el Teorema de Pitágoras.
- Haga que los estudiantes imaginen situaciones reales en donde se pueda aplicar el Teorema de Pitágoras para encontrar alguna medida. Por ejemplo: una escuela tiene un campo de futbol de 100 X 64 metros y se quiere saber cuánto miden las diagonales de la cancha.
2. Demostración
Este apartado tiene una escena. El objetivo es que el alumno constate la validez del Teorema de Pitágoras.
Mediante los vértices se puede mover y deformar un triángulo para recalcar que el Teorema es válido para cualquier triángulo rectángulo. Al terminar hay que presionar Sumar áreas.
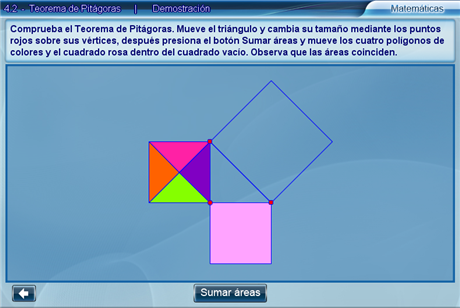
Después, hay que arrastrar los polígonos de colores y el cuadrado rosa hacia el interior del cuadrado vacío, de tal manera que no se encimen ni se salgan del perímetro. Una vez logrado lo anterior, se observa con claridad que la suma de las áreas de los cuadrados pequeños es igual al área del cuadrado grande.
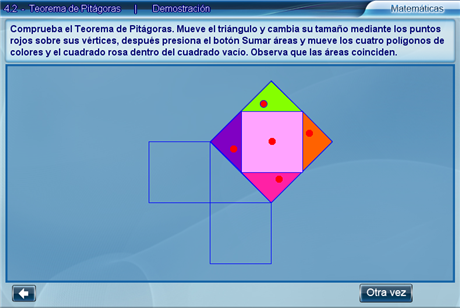
Para repetir el experimento con un triángulo distinto hay que oprimir Otra vez.
Sugerencias didácticas
- Lea las instrucciones en voz alta y cerciórese de que quede claro el objetivo buscado.
- Permita que los alumnos intenten acomodar las piezas en el pizarrón. Pueden pasar de uno en uno, o formar equipos de cinco para acomodar una pieza cada uno.
- Realice varios ejemplos y haga notar que no es determinante la forma del triángulo para que valga el Teorema de Pitágoras, siempre que el triángulo sea rectángulo.
Créditos
Autor
Carlos Alberto Serrato Hernández
Colaboraciones
La unidad fue desarrollada con la colaboración de Carlos Alberto Jaimes Vergara.
Agradecimientos
A Deyanira Monroy Zariñán por su orientación pedagógica.
A Paloma Zubieta López por su apoyo en la redacción.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
