Unidad 4.1
Método de diferencias
Propósito
El
objetivo de esta unidad es que el alumno descubra que los primeros tres
términos de una sucesión cuadrática determinan completamente la fórmula
general de la sucesión y además aprenda a calcularla usando el método
de diferencias.
Instrucciones generales
La unidad se divide en dos apartados:
1. Sucesiones cuadráicas
2. La fórmula de una sucesión cuadrática
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
El botón |
 |
brinda acceso a la ayuda de las escenas interactivas. |
Se puede navegar entre las escenas con las flechas que hay en la parte
inferior de las mismas.
1. Sucesiones cuadráticas
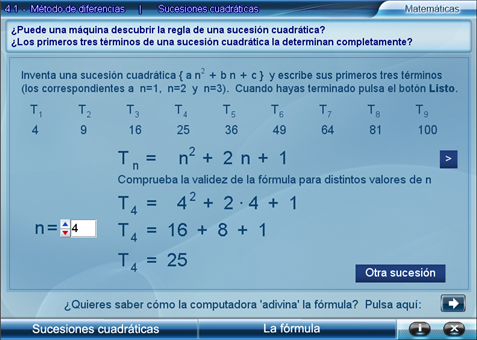
Este apartado tiene una sola escena. El objetivo de esta escena es
motiva el deseo del alumno por saber cómo hace el interactivo para, con
tres términos, descubrir la fórmula.
En ella, se pide al alumno que
invente una sucesión cuadrática y escriba sus primeros tres términos.
El programa responde mostrando la sucesión completa y permite
explorarla para ver cualquier término de ella. También muestra un botón
que al pulsarlo enseñará la regla (fórmula general) de la sucesión.
Sugerencias didácticas
Conviene pedir que todos los alumnos creen su propia sucesión en su
cuaderno, para que luego pasen uno por uno, y planteen su reto a la
computadora. Después de varios ejemplos, es conveniente hacer notar que
no importa cuáles números se pongan, pues el interactivo siempre
encontrará una sucesión cuadrática para la cual esos números son sus
primeros tres términos.
Una vez que los alumnos están lo
suficientemente intrigados, se puede dejar de tarea el intentar
descubrir el secreto del interactivo.
2. La fórmula de una sucesión cuadrática
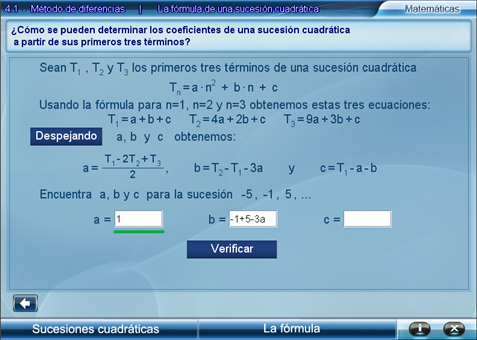
Este apartado también tiene una sola
escena. En ella se presenta el problema de obtener los coeficientes de
una ecuación cuadrática a partir de sus primeros tres términos.
En primer lugar se muestra que el
hecho de que los números dados sean los primeros tres términos de una
sucesión cuadrática lleva a plantear un sistema de tres ecuaciones con
tres incógnitas: a, b y c.
Este sistema de ecuaciones se resuelve fácilmente usando el método de
diferencias pues al restar término a término dos de las ecuaciones
desaparece la variable c y por tanto, con dos de estas diferencias se reduce el problema a un sistema de dos ecuaciones con dos incógnitas: a y b, el cual puede solucionarse por el método de sustitución.
El programa ahora plantea un reto al usuario: dados tres números T1, T2 y T3 , se busca encontrar los coeficientes em>a, b y c
de la sucesión cuadrática, de la cual ellos son los primeros tres
términos. El usuario puede aplicar las fórmulas obtenidas con el método
de diferencias para encontrar a, b y c.
El programa subrayará en rojo las respuestas erróneas y en verde las
correctas. Cuando todas son correctas aparecerá la sucesión completa y
el usuario podrá explorarla a su antojo.
Sugerencias didácticas
Los alumnos pueden pasar por turnos a resolver los retos que el
interactivo plantea. Se debe hacer énfasis en la correcta aplicación de
las fórmulas y, sobre todo, en el manejo de los signos pues el
ejervicio plantea dificultades con números positivos y negativos.
Créditos
Autor
José Luis Abreu León
Colaboraciones
La unidad fue sugerida y parcialmente diseñada por Deyanira Monroy Zariñán.
Esta unidad interactiva fue desarrollada en el
ILCE por el
Grupo Descartes y el equipo de
MATEMÁTICAS III.
Sus
contenidos se distribuyen bajo una licencia de
Creative Commons by-nc-sa. 
La unidad utiliza Descartes
que es software libre.
Adaptación
a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez
(2016)
|
