Unidad 3.5
Gráficas de relaciones funcionales
Referencia curricular
Propósito
Interpretar, construir y utilizar gráficas de relaciones funcionales no lineales para modelar diversas situaciones o fenómenos.
Instrucciones generales
La unidad consta de un apartado:
1. Tiro vertical
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.

El botón |
 |
brinda acceso a la ayuda de las escenas interactivas. |
Se puede navegar entre las escenas con las flechas que hay en la parte inferior de las mismas.
Uso de calculadora
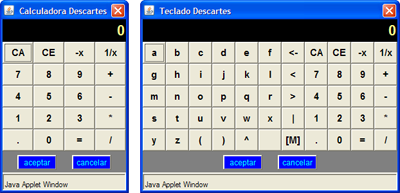
Al hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.
En ambos casos, al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá en el campo de texto o en la celda el último resultado escrito en ella.
Cuando se escribe una expresión numérica como 2^3+4 (el símbolo "^" se utiliza para elevar a una potencia determinada: 2^3 +4 = 23+4), al presionar Aceptar lo que aparecerá será el resultado de la operación, en este caso 12.
Uso de campos de texto
En algunas escenas aparecen campos de texto donde el usuario escribe valores,
expresiones numéricas o algebraicas. Al terminar, en la mayoría
de los casos, se oprime la tecla Intro o un botón con el
símbolo  . Sin embargo, hay ocasiones en que
basta con apretar el botón Verificar o mover el cursor
hacia otro campo de texto. Los usos particulares se detallan en la escena o
el apartado correspondiente.
. Sin embargo, hay ocasiones en que
basta con apretar el botón Verificar o mover el cursor
hacia otro campo de texto. Los usos particulares se detallan en la escena o
el apartado correspondiente.
1. Tiro vertical
En esta unidad se presenta la simulación de un experimento de tiro vertical. Se busca que los alumnos identifiquen y sustituyan las variables que intervienen en la ecuación para calcular la altura a la que se encuentra un objeto lanzado verticalmente desde una altura inicial.
La unidad consta de un apartado con dos pasos secuenciales. Una vez que se introducen correctamente los valores que se pide, ya por medio de campos de texto o puntos de la gráfica, se aprieta el botón Verificar y se avanza al siguiente paso.
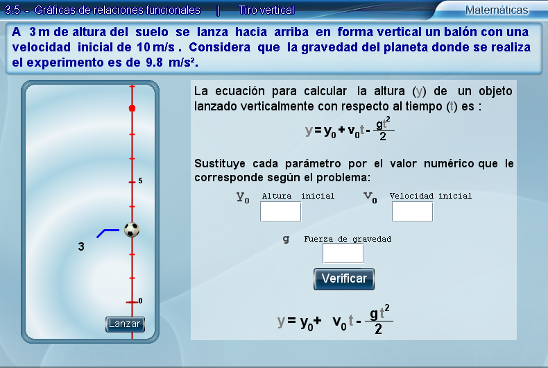
En la escena se pide al alumno que coloque el valor de cada variable en el campo de texto que le corresponde. Si el valor que se introduce es el correcto, el campo de texto se deshabilita y el valor se sustituye automáticamente en la ecuación que se encuentra en la parte inferior. Por el contrario, si el valor es incorrecto, un recuadro rojo aparecerá en el campo de texto indicando que debe corregirse.
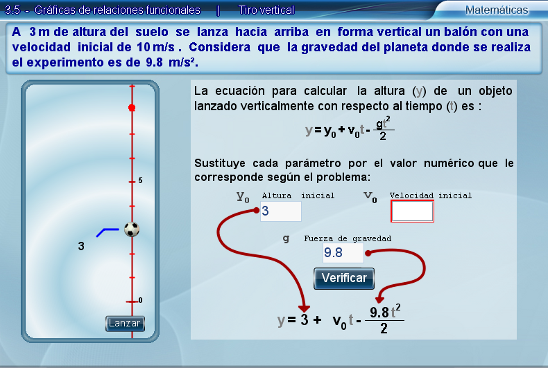
Una vez que el alumno llenó correctamente cada campo de texto, se avanza al siguiente paso y en esta ocasión, se le solicita que dibuje al menos diez puntos de la gráfica que resultaría de la ecuación que sustituyó en la sección anterior.
A continuación se explica cada una de las partes de la escena.
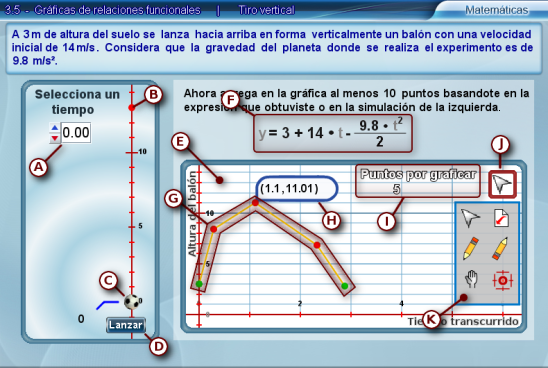
- Este pulsador sirve para seleccionar el tiempo del cual se quiere conocer la altura. Al presionar Lanzar, este valor será el tiempo que durará la animación y permitirá ver la altura que alcanzó el balón en ese tiempo.
- Este punto rojo muestra la altura máxima que puede alcanzar el balón.
- Balón del experimento.
- Con el botón Lanzar se inicia la animación.
- Panel que contiene las herramientas para graficar los puntos solicitados por el interactivo.
- Es la ecuación para calcular la altura del objeto con base en el tiempo transcurrido en el tiro vertical con los valores sustituidos para el problema actual.
- Ejemplo de la gráfica que el alumno pintará al colocar los puntos con las herramientas.
- Muestra las coordenadas del punto dibujado, editado o seleccionado con alguna de las herramientas (ver inciso K).
- Cuantos puntos hacen falta por graficar antes que el interactivo permita verificar (muestre el botón Verificar).
- Despliega u oculta el panel de herramientas para graficar.
-
Panel de las herramientas disponibles.
-
 Permite seleccionar un punto para ver sus coordenadas o
mover el área de la gráfica que se está despegando.
Permite seleccionar un punto para ver sus coordenadas o
mover el área de la gráfica que se está despegando. -
 Limpia el área para graficar al eliminar todos
los puntos.
Limpia el área para graficar al eliminar todos
los puntos. -
 Sirve para dibujar un punto a la vez.
Sirve para dibujar un punto a la vez. -
 Borra un solo punto.
Borra un solo punto. -
 Permite cambiar la posición de un punto ya dibujado.
Permite cambiar la posición de un punto ya dibujado.
-
 Regresa el área de la gráfica desplegada a su posición
original.
Regresa el área de la gráfica desplegada a su posición
original.
-
Para saber las posiciones de los puntos que deben dibujarse, se puede utilizar como x un tiempo t y evaluarlo en la ecuación (inciso F de la imagen anterior), seleccionando un tiempo en el panel de la izquierda, al presionar el botón Lanzar se hará la simulación del tiro vertical pero se detendrá al llegar al tiempo seleccionado. Con esto se puede ver la altura que alcanza el balón al transcurrir t segundos.
Una vez dibujados al menos 10 puntos, el interactivo permite verificar. Si algún punto está mal colocado, aparecerá de color rojo y el interactivo lo señalara.
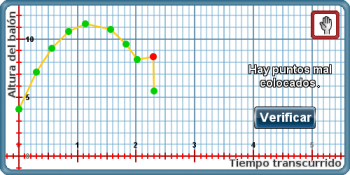
Por otro lado, si todos los puntos son correctos pero no son una parte representativa o no reflejan suficientes características de la gráfica completa, el interactivo pedirá que se separen los puntos o que se agreguen más.
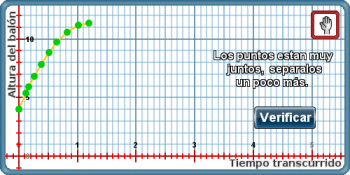
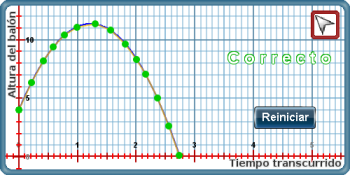
Una vez que los puntos estén bien distribuidos a lo largo de la gráfica, se presiona Verificar. Cuando el interactivo muestra que es correcto, termina la actividad.
Sugerencias didácticas
Es conveniente que haga a los alumnos preguntas como:
-
¿Cuánto tiempo tardará el balón en caer al suelo?
- ¿Cuál es la altura máxima que puede alcanzar el balón y en qué tiempo la alcanza?
- ¿En qué tiempo el balón lanzado se encuentra a una altura de cinco metros?
Al contestar cada pregunta, solicite que expliquen cómo obtuvieron la respuesta y si no utilizaron la gráfica señale cómo a partir de ella se podría haber obtenido la misma información, por ejemplo:
-
¿Cuánto tiempo tardará el balón en caer al suelo?
Observe en qué punto la gráfica corta al eje x, en nuestro ejemplo a los 2.7 seg. aproximadamente.
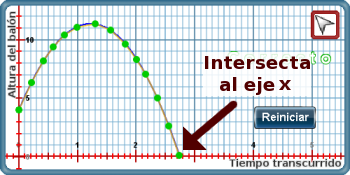
-
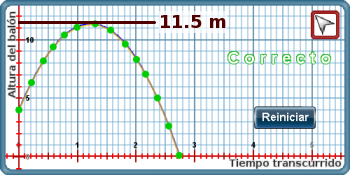
¿Cuál es la altura máxima que puede alcanzar el balón y en qué tiempo la alcanza?
Busque la mayor altura del balón en la gráfica, aproximadamente a los 11.5 metros al tiempo igual a 1.2 segundos
-
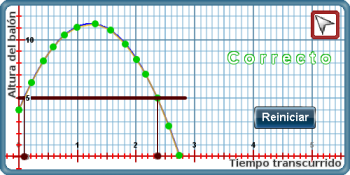
¿En qué tiempo el balón lanzado se encuentra a una altura de cinco metros?
Identifique en qué puntos la gráfica se encuentra a esa altura. La respuesta es aproximadamente a los 0.1 y 2.3 segundos. En este caso es importante hace notar que en la gráfica se aprecia claramente que hay dos instantes en los cuales está a esa altura.
Créditos
Autor
Oscar Escamilla González
Colaboraciones
La unidad fue desarrollada con los
lineamientos y asesoría didáctica y pedagógica de Deyanira Monroy
Zariñán y José Luis Abreu León.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
