Unidad 1.6
La razón de cambio
Referencia curricular
Propósito
Analizar la razón de cambio de un proceso o fenómeno que se modela con una función lineal y relacionarla con la inclinación o pendiente de la recta que lo representa.
Instrucciones generales
La unidad se divide en tres apartados:
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior. Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
|
Se puede navegar entre las escenas con las flechas que hay en la parte inferior de las mismas.
Uso de calculadora
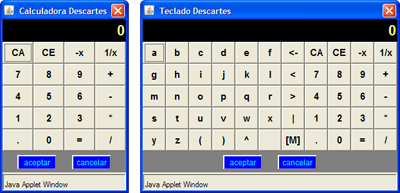
Al hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.
En ambos casos, al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá en el campo de texto o en la celda el último resultado escrito en ella.
Cuando se escribe una expresión numérica como 2^3+4 (el símbolo "^" se utiliza para elevar a una potencia determinada: 2^3 +4 = 23+4), al presionar Aceptar lo que aparecerá será el resultado de la operación, en este caso 12.
Uso de campos de texto
En algunas escenas aparecen campos de texto donde el usuario escribe valores,
expresiones numéricas o algebraicas. Al terminar, en la mayoría
de los casos, se oprime la tecla Intro o un botón con el
símbolo 
. Sin embargo, hay ocasiones en que
basta con apretar el botón Verificar o mover el cursor
hacia otro campo de texto. Los usos particulares se detallan en la escena o
el apartado correspondiente.
1. Exploración
La escena muestra una recta sobre la que el alumno puede seleccionar dos puntos, ya sea con los pulsadores que están en la tabla o al moverlos sobre la gráfica. Presentan también, numérica y gráficamente, las diferencias entre las coordenadas de cada punto seguido del resultado de la división de estas diferencias. Se guía a los alumnos a través de una serie de preguntas para que deduzcan que esta relación es constante para cualquier par de puntos y que su valor depende de la inclinación de la recta.
A continuación, se enlistan los controles con una breve explicación de su funcionamiento.
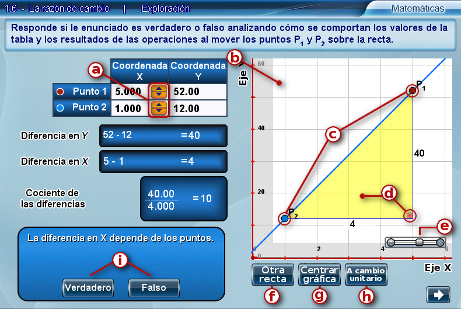
- a) Pulsadores
- Estos modifican la coordenada x del punto P1 o del punto P2 según sea el caso.
- b) Espacio gráfica
- Aquí se dibujan la recta dada y los puntos seleccionados por el alumno. Esta zona es interactiva y permite cambiar el área visible de la gráfica arrastrándola dentro del espacio.
- c) Controles gráficos
- Estos pueden arrastrarse para seleccionar las coordenadas de los puntos que se quiera comparar. Los controles gráficos sólo se moverán sobre la recta.
- d) Polígono de diferencias
- Este muestra las diferencias en las coordenadas de los puntos seleccionados. El cuadrado de la esquina inferior derecha funciona para mover los puntos simultáneamente conservando la distancia entre ellos (por lo que las diferencias en las coordenadas se mantienen constantes).
- e) Control de escala
- Acerca o aleja la gráfica.
- f) Otros valores
- Vuelve a iniciar la escena, cambia la pendiente de la recta y reacomoda los puntos.
- g) Centrar gráfica
- Acomoda la escala y el área visible de la gráfica para que veamos los puntos seleccionados y el origen (la coordenada (0,0));
- h) A cambio unitario
- Deja el punto P1 fijo y posiciona P2 de tal manera que la variación en la coordenada x sólo sea de 1 unidad.
- i) Botones Verdadero y Falso
-
Como se mencionó en la introducción del apartado, esta escena trata de dirigir a los alumnos a
ciertas conclusiones. Se les pide a los alumnos que marquen si el postulado escrito en el recuadro
azul es verdadero o falso. Si la respuesta es correcta, el interactivo muestra el siguiente
enunciado para responder. En caso de que la respuesta seleccionada sea incorrecta el interactivo
proporciona una pequeña instrucción para encaminarlos a contestar correctamente.
Por ejemplo:
Sugerencias didácticas
Haga con los alumnos este análisis, tomemos el siguiente ejemplo:
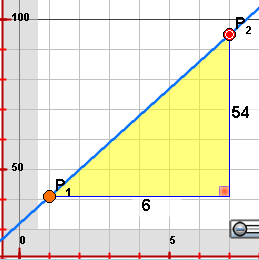
Se puede sugerir a los alumnos que imaginen que recorren el polígono amarillo
por el contorno azul oscuro. Entonces, para llegar de P1 a
P2, necesitan avanzar 6 unidades en el eje x
y subir 54 unidades en el eje y. Pero pueden tomar otro camino,
avanzar una unidad en el eje x y subir nueve unidades
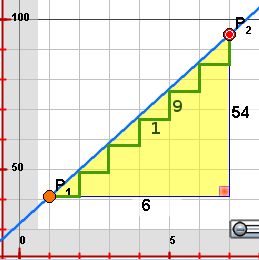
Mencionado esto, haga notar que el nueve coincide con el valor de la relación entre las diferencias. Además, aclare que esa relación se puede interpretar como cuánto debe desplazarse a partir de P1 por el eje y, por cada unidad que se avance en el eje x para llegar P2. Por último, resalte que este valor es constante para cualquier par de puntos sobre una recta.
2. Problemas
En este apartado se les pide a los alumnos que obtengan información de la gráfica que representa una relación proporcional, con la intención de que utilicen lo aprendido en los cursos anteriores como coordenadas en el plano cartesiano, interpretación de gráficas, etc.
Además se les ejercita en el método para calcular la pendiente de una recta conociendo dos puntos sobre ella, y se refuerza la idea del apartado anterior de interpretar la razón de cambio como una relación: cuánto hay que desplazarse en el eje y por cada unidad que se avance en el eje x. Por último, se busca que interpreten esta razón dentro de la situación concreta que se plantea.
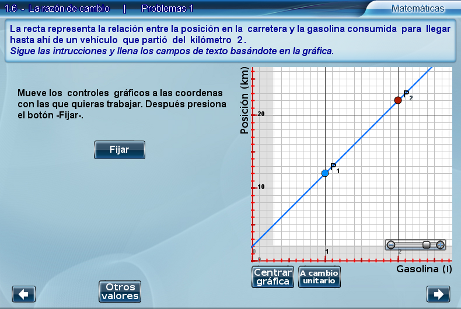
Todas las escenas de este apartado comienzan indicando a los alumnos que seleccionen dos puntos. Esto es desplazando los puntos P1 y P2 sobre la recta, a continuación fijarlos en las coordenadas que deseen para trabajar presionando el botón Fijar.
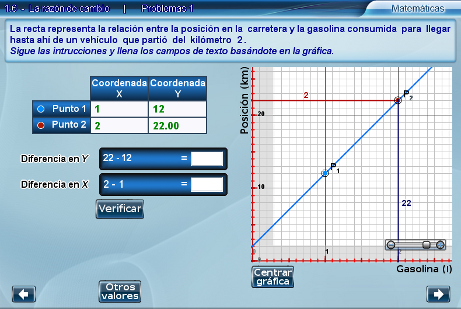
Después se deben introducir los valores de las coordenades de los puntos en una tabla. Una vez que las coordenadas que escribieron en la tabla coinciden con las coordenadas de P1 y P2, aparecen los campos donde escribir las diferencias entre las coordenadas en el eje y y en el eje x respectivamente.
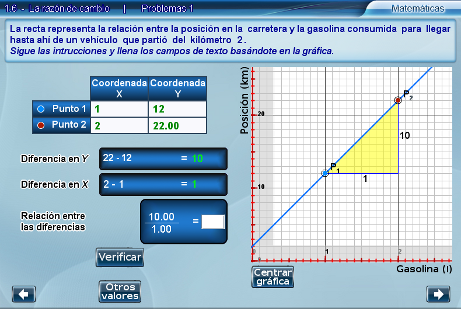
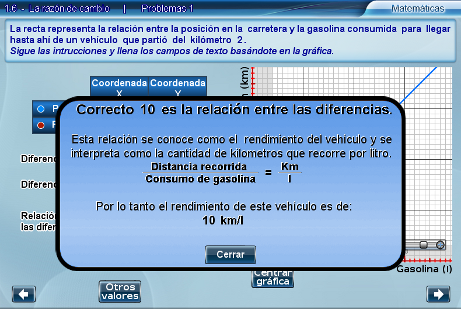
Cuando se han introducido los valores correctos de las diferencias, el interactivo pide que se escriba el valor de la división de estas dos cantidades y si es correcto muestra una ventana emergente con la explicación de lo que este valor significa en el contexto de la situación planteada.
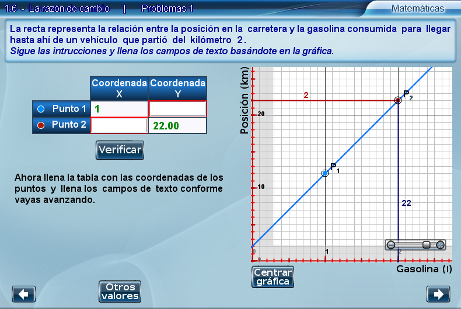
Por último, cabe mencionar que cuando el valor introducido en algún campo de texto sea incorrecto, se dibujará sobre este un borde rojo. Un campo de texto vacío no es tomado en cuenta para evaluar, pero si no se llenan todos los campos, el interactivo no permite avanzar.
3. Comparación
El último apartado está pensado para reforzar la idea de que la pendiente de la recta y la razón de cambio son equivalentes. Se pide a los alumnos que comparen el rendimiento de dos vehículos. Se muestran las rectas que modelan cada situación y dos puntos sobre cada una de ellas. En este nivel se espera que los alumnos con sólo ver las gráficas, sepan cuál de los dos vehículos tiene mejor rendimiento o si tienen el mismo.
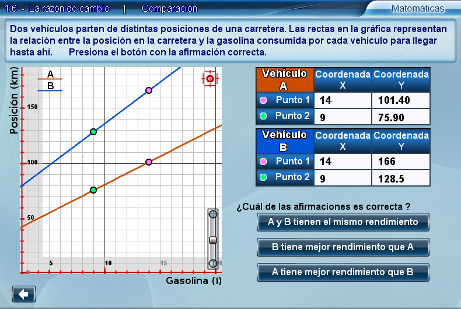
Sugerencias didácticas
Si los alumnos tienen aún dificultad para responder correctamente, haga que calculen el rendimiento de los vehículos a partir de los puntos dados sobre la recta como en los apartados anteriores.
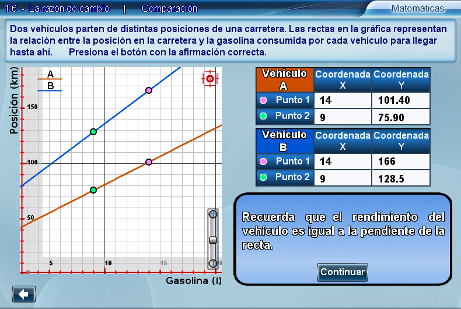
Tomando como ejemplo los valores de los puntos en la imagen anterior tendríamos:
Vehículo A
| 101.4 - 75.9 | = | 25.5 | = | 5.1 km/l |
| 14 - 9 | 5 |
Vehículo B
| 166 - 128.5 | = | 37.5 | = | 7.5 km/l |
| 14 - 9 | 5 |
Por lo que el vehículo B tiene mejor rendimiento que el vehículo A.
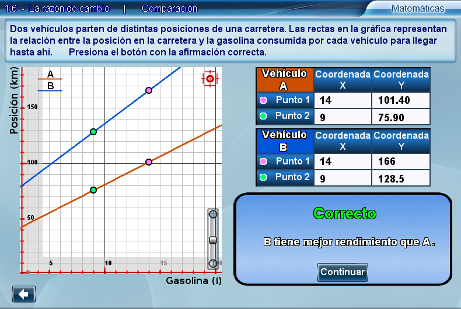
Después de hacer las operaciones y encontrar la respuesta correcta, señale a los alumnos que el vehículo con mejor rendimiento es aquel cuya recta tiene la mayor pendiente o dicho en otras palabras, es aquel cuya recta es más vertical.
Créditos
Autor
Oscar Escamilla González
Colaboraciones
La unidad fue desarrollada con los lineamientos y asesoría didáctica y
pedagógica de Deyanira Monroy Zariñán y José Luis Abreu León.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de
La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)