Unidad 1.4Ángulos en la circunferenciaReferencia curricularPropósitoDeterminar la relación entre un ángulo inscrito y un ángulo central de una circunferencia, si ambos abarcan el mismo arco. Instrucciones generalesLa unidad se divide en tres apartados: 1. Explorar Se puede navegar entre los
apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
Los dos botones que se
encuentran en la parte derecha tienen la función siguiente:
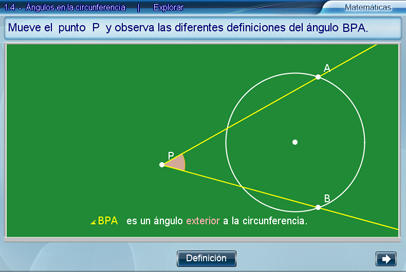
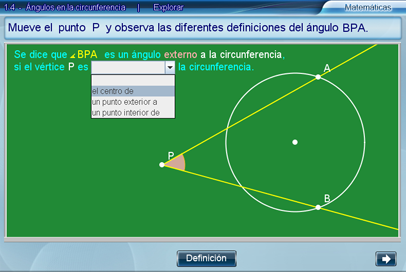
Se puede navegar entre las escenas con las flechas que hay en la parte inferior de las mismas. 1. ExplorarEste apartado está constituido por una escena: Explorar En esta escena se busca que el alumno estudie las definiciones de los ángulos relacionados con la circunferencia, tales como ángulo inscrito, ángulo central, ángulo exterior y ángulo interior.  El ángulo de la escena está formado por los puntos: A, P y B. Dichos puntos se pueden seleccionar con el ratón y mover en el pizarrón, con las siguientes restricciones: el punto P se puede arrastrar por todo el pizarrón mientras que los puntos A y B únicamente se pueden mover sobre la circunferencia. Con esto, el ángulo dado se modifica también.
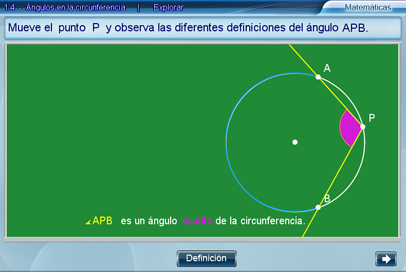
Además, la circunferencia puede ser modificada dinámicamente. Esto resulta conveniente para el alumno y su proceso de exploración.
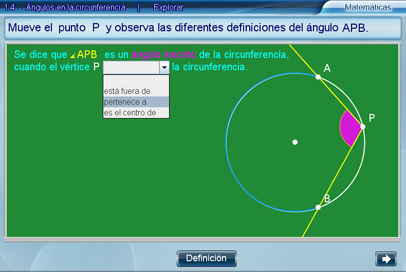
Las definiciones son interactivas, con la intención de que el alumno complete los campos seleccionando la opción correcta en cada caso para la definición correspondiente. Cuando el
ángulo sea inscrito o central, el arco subtendido se representa con
color verde en
el interactivo. Sugerencias didácticasSe sugiere explicar al alumno el significado de que un ángulo subtienda o contenga un arco de la circunferencia. 2. MedicionesEste apartado consta de una escena: Mediciones
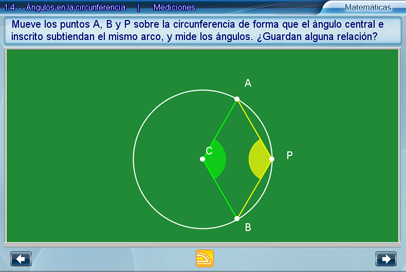
El objetivo es proporcionar al estudiante las herramientas de medición que le permitan observar alguna relación entre un ángulo inscrito y un ángulo central que subtiendan el mismo arco de la circunferencia.
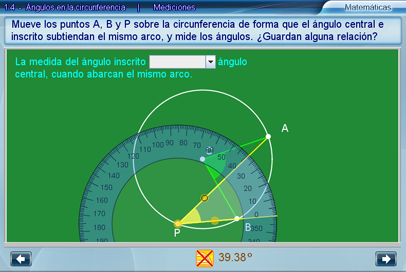
Si bien las mediciones no son exactas pues existen ángulos cuyas expresiones decimales no son periódicas, se realizó un especial esfuerzo por establecer cálculos redondeados o aproximados que respetaran la relación de proporción doble entre el ángulo inscrito y el ángulo central. Cualquier variación sutil en las mediciones sobre otros ángulos de la figura, responde a las imprecisiones lógicas del cálculo por redondeo y aproximación.
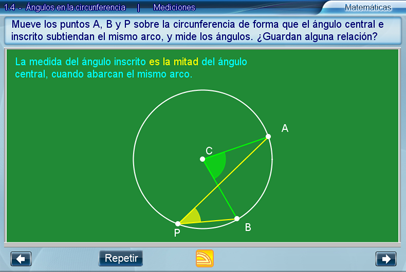
Sugerencias didácticasEn esta escena se recomienda efectuar mediciones que lleven a la idea o hipótesis de que el ángulo inscrito es la mitad del ángulo central siempre que abarquen (subtiendan) el mismo arco de la circunferencia (recordemos que estamos dejando fijo al ángulo ACB el cual subtiende un arco dado). Para lo anterior hay que fijar los puntos A y B en un lugar y variar el punto P. Advertir además que, en todos los casos, el ángulo APB mide lo mismo siempre que no se cambie el arco subtendido en la circunferencia. 3. PropiedadesEn este apartado se demuestra la siguiente propiedad: Cuando un ángulo inscrito y uno central subtienden el mismo arco, entonces el ángulo central es igual al doble del ángulo inscrito. Para demostrar esta importante propiedad, se consideran tres posibles casos para dichos ángulos, es decir, siempre que un ángulo inscrito y un ángulo central subtiendan el mismo arco entonces, sucederá una y solo una de las tres situaciones siguientes: 1) En la configuración, uno de los segmentos que definen al ángulo inscrito es un diámetro de la circunferencia. 2) En la configuración, uno de los segmentos que definen al ángulo inscrito intersecta uno de los segmentos que definen al ángulo central, en un punto distinto a los extremos del arco subtendido por los ángulos y distinto a los vértices de los mismos. 3) En la configuración, los lados de los segmentos que definen a los ángulos, únicamente se intersectan en los extremos del arco subtendido. Es importante subrayar que cualquier otra configuración que se piense entre dichos ángulos, será un ejemplo de uno y sólo uno de los tres casos anteriores. En este sentido se justifica que la propiedad en general queda demostrada, siempre que demostremos que se cumple para cada uno de los tres casos anteriores. Propiedades 1
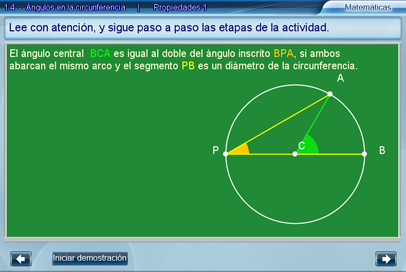
El objetivo de esta escena, es proporcionar al alumno una demostración de la relación entre el ángulo inscrito y el ángulo central, para el primer caso considerado, es decir cuando uno de los segmentos del ángulo inscrito es un diámetro de la circunferencia.
Como antes, la interacción se complementa con menús donde el estudiante selecciona la respuesta correcta para que la explicación evolucione hasta concluir la demostración.
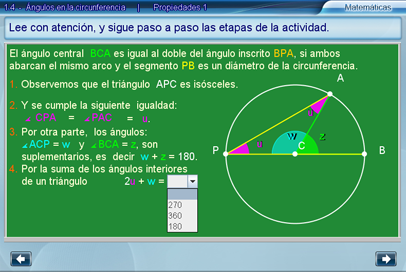
Esta demostración, que únicamente aplica para el caso en que el segmento PB es un diámetro de la circunferencia, es un excelente ejercicio preparativo para una posterior demostración general.
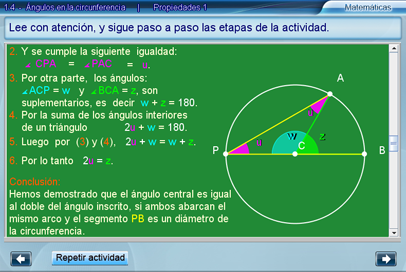
Al pie de la escena se concluye el ejercicio y se muestra un resumen. Propiedades 2En esta escena se demuestra que la propiedad se cumple para el segundo caso considerado, esto es, cuando el cuadrilátero ABPC tiene por diagonales un lado del ángulo BCA y un lado del ángulo BPA. Tal es el caso estudiado, como se muestra en la siguiente imagen.
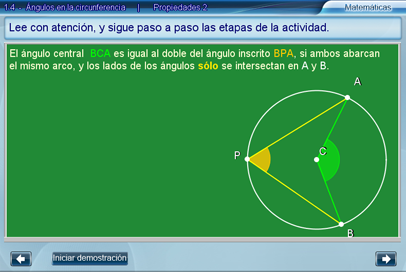
Como antes, la interacción está dada por opciones múltiples de respuesta, con el fin de que el alumno escoja la correcta, pero también de que se involucre en el proceso lógico de razonamiento que subyace a la demostración.
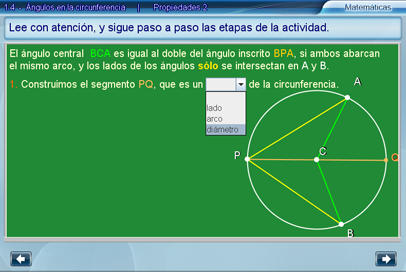
En todo momento se puede utilizar el transportador, recordando que nuestra herramienta de medición hace cálculos aproximados.
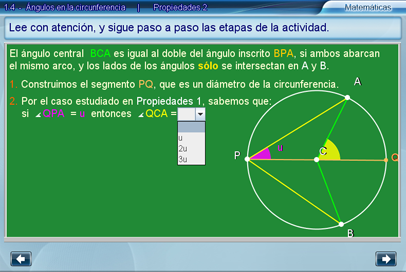
El estudiante ya debe estar familiarizado con expresiones algebraicas, por ello se parte del supuesto de que podrá manejar la notación. En cualquier caso, se utilizan colores como ayuda visual para identificar los ángulos: colores iguales representan ángulos iguales.
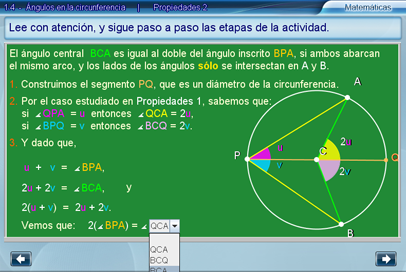
Al terminar la demostración, Conclusión muestra la idea final del trabajo realizado.
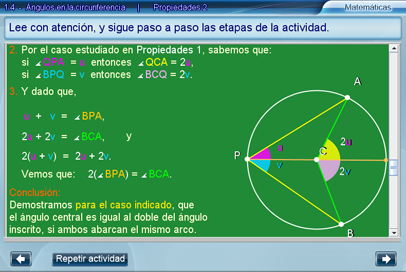
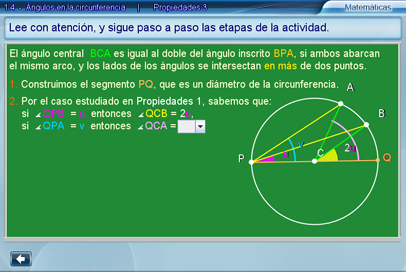
Propiedades 3En esta escena se demuestra que la propiedad se cumple para el tercer caso considerado, esto es, cuando el cuadrilátero ACBP no tiene por diagonales ningún segmento del ángulo BCA o del ángulo BPA, como se hace panente en la siguiente imagen.  Existen opciones múltiples de respuesta, con el fin de que el alumno escoja la correcta, y se involucre en el proceso lógico de razonamiento que subyace a la demostración.  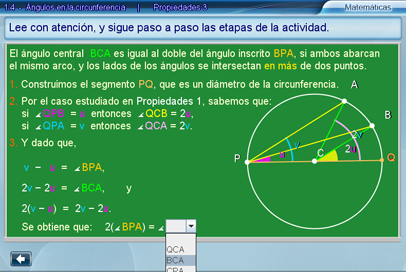En todo momento es posible utilizar el transportador.  Al terminar la demostración, Conclusión exhibe los resultados del trabajo realizado. Sugerencias didácticasAclare con los estudiantes que otra manera de nombrar a los ángulos es con una sola letra, lo cual a simplifica la notación. Es muy importante corroborar con los alumnos que cualquiera de las posibles configuraciones en que podamos presentar un par de ángulos (inscrito y central) tales que subtiendan un mismo arco de la circunferencia, está contemplada en uno y solo uno de los tres casos estudiados. Créditos
Autor Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
Brinda acceso a la ayuda de las escenas interactivas.
Cierra
la ventana.
