Unidad 1.3Rectas y CircunferenciasReferencia curricularPropósitoDeterminar, mediante construcciones, las posiciones relativas entre rectas y una circunferencia y entre circunferencias. Caracterizar la recta secante y la tangente a una circunferencia. Identificar las posiciones relativas entre una recta y una circunferencia y entre circunferencias. Estudiar algunas propiedades de las rectas secante y tangente de una circunferencia. Identificar que una recta tangente a una circunferencia es perpendicular al radio que pasa por el punto de tangencia. Instrucciones generalesLa unidad consta de dos apartados: 1. Rectas Se puede navegar entre los
apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
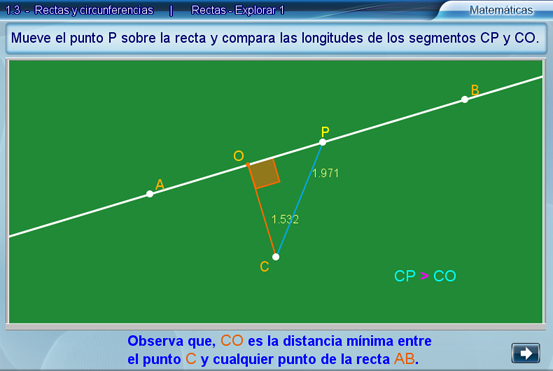
Se puede navegar entre las escenas con las flechas que hay en la parte inferior de las mismas. 1. RectasEste apartado está constituido por cuatro escenas: Rectas - Explora 1En esta escena se busca que el alumno recuerde la definición de la distancia de un punto C dado, a una recta dada AB, esto es, la distancia de C al punto O, que es la intersección de la recta que pasa por C y es perpendicular a AB. Asimismo es importante señalar las propiedades que resultan, por ejemplo: la longitud CO (que es la distancia de C a la recta AB), es la mínima longitud posible de un segmento con vértices en C y cualquier otro punto P en la recta AB. Por esta razón se le pide al alumno que mueva a P sobre la recta, observe las longitudes del segmento CP y que las compare con la longitud del segmento CO, naturalmente dichas longitudes serán iguales únicamente cuando P sea igual a O. Es pertinente observar que la noción de distancia de un punto dado a una recta dada está bien definida, esto es, que no depende del punto ni de la recta; por ejemplo el punto C podría haber estado contenido en la misma recta AB y en tal caso la distancia sería igual a cero.
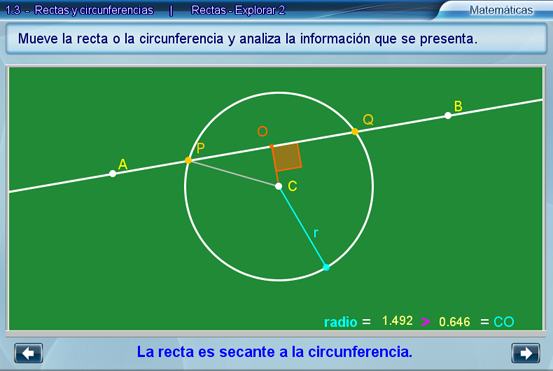
Rectas - Explora 2La intención de la escena es que el alumno explore, junto con el maestro, por qué se dice que la recta es secante, tangente o ajena a la circunferencia (según el caso). En todo momento será fundamental tener presente el concepto de distancia de un punto dado a una recta dada. Se recomienda identificar alguna relación entre el radio de la circunferencia con centro en C y la distancia de C a la recta AB, cuando la recta sea ajena, secante o tangente.
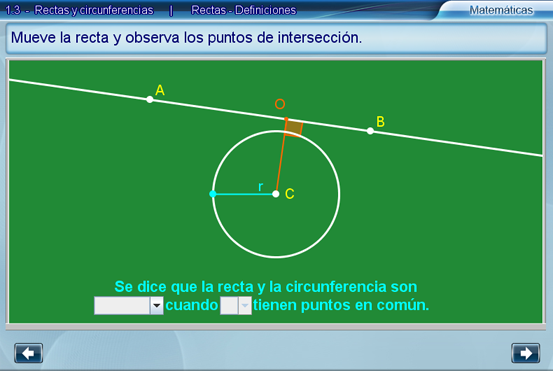
Rectas - DefinicionesEl
objetivo de la escena es definir (respectivamente) los conceptos de recta ajena,
tangente
y secante a una circunferencia dada. Por ello,
es
importante sugerir al alumno que sea la recta la que mueva
hasta generar los casos de recta secante y tangente; esto, con la
finalidad de enfatizar que las relaciones
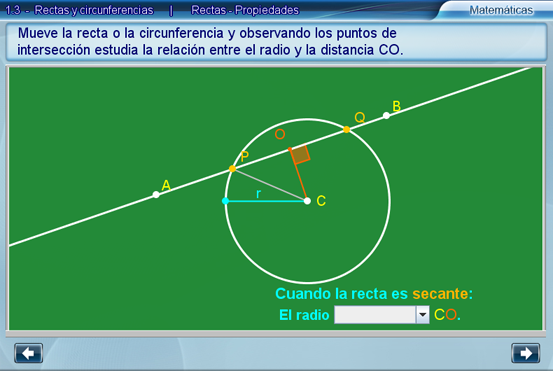
Rectas - PropiedadesEn esta escena se busca que el alumno haga suyos los conceptos definidos. Que analice y mencione algunas propiedades derivadas de estas definiciones. Las construcciones geométricas dinámicas permiten explorar una gran cantidad de casos en los cuales el alumno podrá observar las relaciones geométricas intrínsecas.
Sugerencias didácticasPara la escena de Definiciones, se sugiere hacer preguntas como: ¿En cuántos puntos puede intersectar la recta AB a la circunferencia C? También se pueden hacer señalamientos como: si el radio de la circunferencia es mayor o igual a la distancia entre el punto C y la recta AB, entonces existen puntos comunes entre la recta y la circunferencia. Para la escena Propiedades, se recomienda decir a los alumnos que realicen las mediciones sugeridas y comprueben qué propiedades son independientes de la recta tangente que seleccionaron y cuáles son independientes de la recta secante elegida. No
obstante, el recurso de medición no representa un método demostrativo
de ninguna propiedad, únicamente
nos permite explorar casos y generar
conjeturas o hipótesis que posteriormente serán propiamente
demostradas. El recurso de medición también es un excelente medio de
confirmar, para un caso particular, alguna propiedad
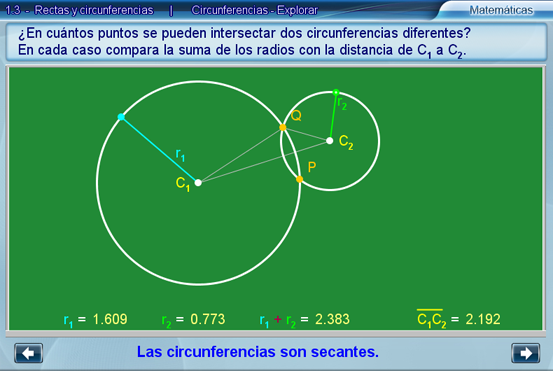
general ya demostrada. 2. CircunferenciasEste apartado consta de tres escenas. Circunferencias - ExplorarEl objetivo de esta escena es proporcionar los elementos geométricos dinámicos y métricos necesarios para explorar, los conceptos de circunferencias ajenas, secantes y tangentes.
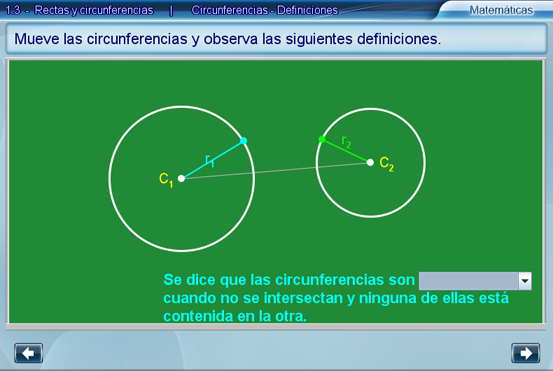
Circunferencias - DefinicionesEl objetivo de esta escena, es definir cuándo dos circunferencias son tangentes o secantes y observar los distintos tipos de casos. Por ejemplo, tangencia interior o exterior.
Circunferencias - PropiedadesEn esta escena se reunen los elementos necesarios y las definiciones correspondientes para determinar las propiedades que resultarán de dichas relaciones entre las circunferencias. Por ejemplo, en la siguiente figura las circunferencias se definen como ajenas, de donde resulta como una propiedad que la distancia entre sus centros es estrictamente mayor que la suma de sus radios.
Sugerencias didácticasPara la escena de Exploración, se sugiere que hacer preguntas inductivas como: ¿En cuántos puntos pueden intersectarse dos circunferencias distintas? Es importante señalar que, si las dos circunferencias tienen el mismo radio y el mismo centro, entonces las circunferencias son iguales. En este caso tienen en común todos sus puntos. Para la escena de Definiciones, podemos hacer preguntas como: ¿Qué condiciones se necesitan para que las circunferencias sean tangentes o secantes? Para la escena de Propiedades, es importante observar y señalar que algunas condiciones son necesarias para que las circunferencias sean tangentes o secantes. Sin embargo puede que no sean suficientes, es decir, que no basten para abarcar todos los casos, por ejemplo: "si la suma de sus radios es igual a la distancia entre sus centros, entonces las circunferencias son tangentes", observemos que esta condición no es suficiente ya que pueden ser tangentes y no cumplir con la condición mencionada, dicho caso ocurre cuando las circunferencias son interiormente tangentes. Créditos
Autor Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
