Unidad 1.2
Triángulos y cuadriláteros
Referencia curricular
Propósito
Que los alumnos exploren mediante la geometría dinámica cuadriláteros y sus diagonales para comprobar que las diagonales se intersectan en su punto medio si y sólo si el cuadrilátero es un paralelogramo.
Instrucciones generales
La unidad se divide en dos apartados:
- Lados opuestos
- Diagonales
Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.

|
En la parte inferior de cada escena hay dos flechas para navegar entre las escenas.
1. Lados opuestos
Este apartado tiene cinco escenas.
El objetivo es que el alumno concluya, con ayuda de los criterios de congruencia de triángulos, que un cuadrilátero es un paralelogramo si y sólo si sus lados opuestos miden lo mismo.
Lados opuestos 1
Primeramente, arrastrando los vértices de un cuadrilátero el alumno deberá modificarlo hasta que sus lados sean paralelos. El botón Medidas activa la visualización de las medidas de los lados del cuadrilátero, y el botón Rectas permite ver la prolongación de los lados.
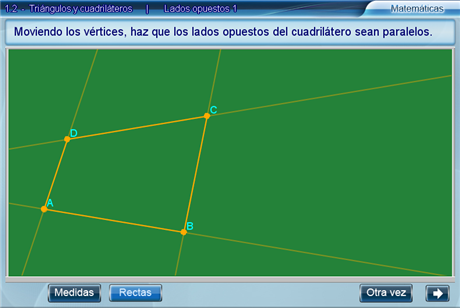
Enseguida, el alumno deberá responder si los lados opuestos son iguales utilizando dos listas desplegables. Para intentar con otro cuadrilátero hay que presionar el botón Otra vez.
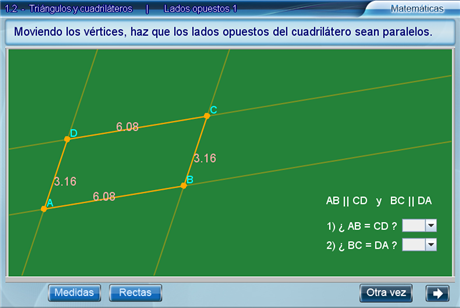
Lados opuestos 2
Paso a paso, el alumno deberá completar la demostración de la primera proposición.
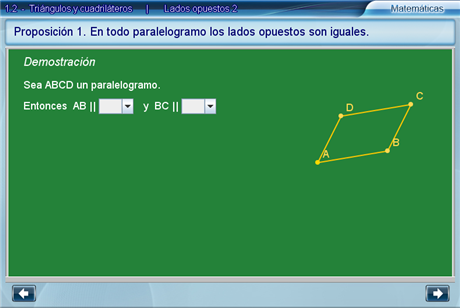
Al final, se tiene la argumentación completa en pantalla.
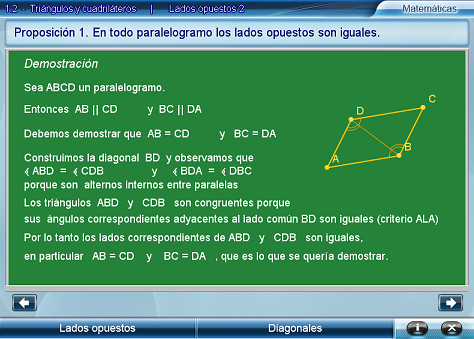
Lados opuestos 3
Primeramente, arrastrando los vértices de un cuadrilátero el alumno deberá modificarlo hasta que sus lados sean iguales. El botón Medidas activa la visualización de las medidas de los lados del cuadrilátero, y el botón Rectas permite ver la prolongación de los lados.
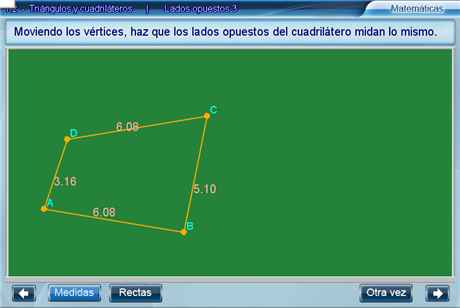
Enseguida, el alumno deberá responder si los lados opuestos son paralelos utilizando dos listas desplegables. Para intentar con otro cuadrilátero hay que presionar el botón Otra vez.
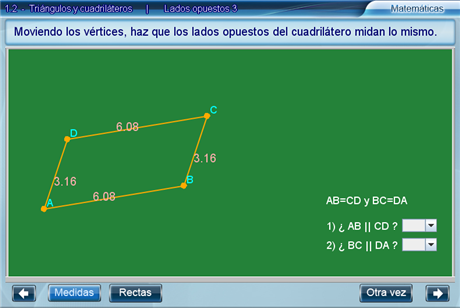
Lados opuestos 4
Paso a paso, el alumno deberá completar la demostración de la segunda proposición.
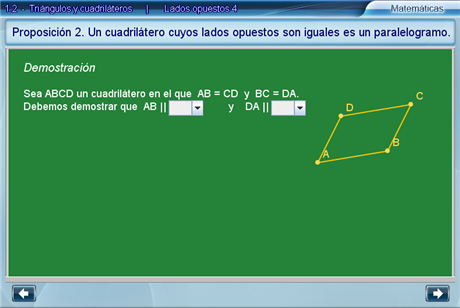
Al final, se tiene la argumentación completa en pantalla.
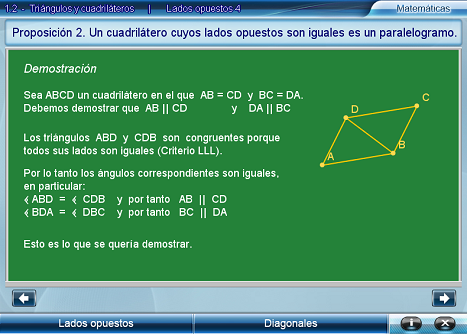
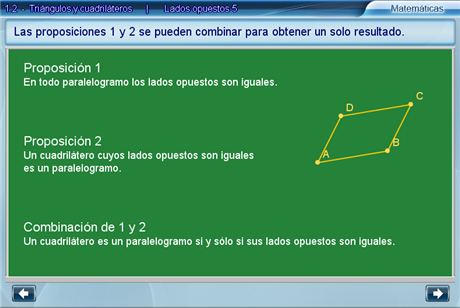
Lados opuestos 5
Como conclusión, se muestra la forma de combinar las proposiciones 1 y 2 en un solo resultado.
Sugerencias didácticas
-
En cada escena lea las instrucciones en voz alta y cerciórese de que quede claro el objetivo buscado.
-
Realice varios ejemplos y haga notar que en el esquema final no es determinante la forma del paralelogramo para llegar al resultado.
-
Si lo considera apropiado, puede mencionar que el resultado nos da una caracterización de los paralelogramos.
2. Diagonales
Este apartado tiene cinco escenas.
El objeto del segundo apartado es que el alumno concluya, con ayuda de los criterios de congruencia de triángulos, que un cuadrilátero es un paralelogramo si y sólo si sus diagonales se bisectan mutuamente.
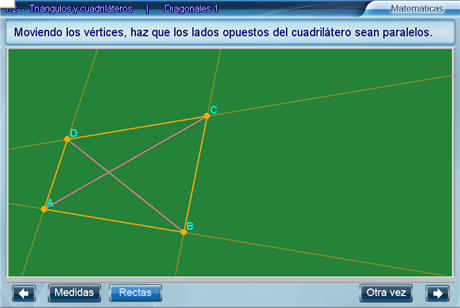
Diagonales 1
Primeramente, arrastrando los vértices de un cuadrilátero el alumno deberá modificarlo hasta que sus lados sean paralelos. El botón Medidas activa la visualización de las medidas de los lados del cuadrilátero, y el botón Rectas permite ver la prolongación de los lados.
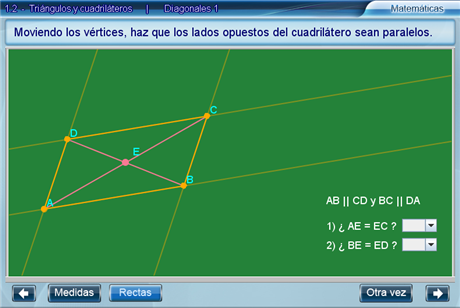
Enseguida, el alumno deberá responder si las diagonales se intersectan en sus puntos medios utilizando dos listas desplegables. Para intentar con otro cuadrilátero hay que presionar el botón Otra vez.
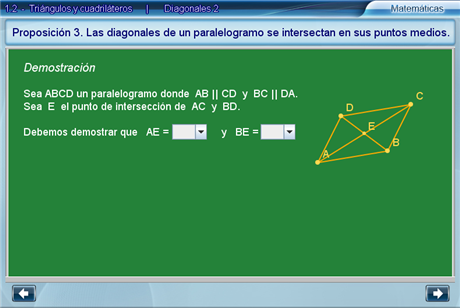
Diagonales 2
Paso a paso, el alumno deberá completar la demostración de la tercera proposición.
Al final, se tiene la argumentación completa en pantalla.

Diagonales 3
Primeramente, arrastrando los vértices de un cuadrilátero el alumno deberá modificarlo hasta que sus diagonales se intersecten en sus puntos medios. El botón Medidas activa la visualización de las medidas de los lados del cuadrilátero, y el botón Rectas permite ver la prolongación de los lados.
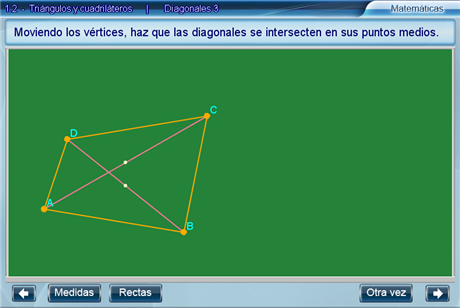
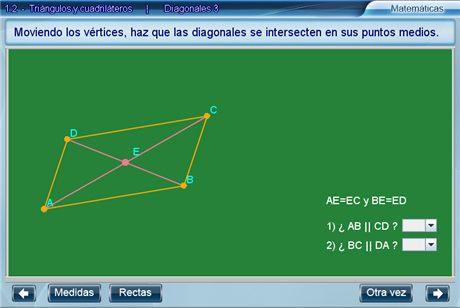
Enseguida, el alumno deberá responder si los lados opuestos son paralelos utilizando dos listas desplegables. Para intentar con otro cuadrilátero hay que presionar el botón Otra vez.
Diagonales 4
Paso a paso, el alumno deberá completar la demostración de la cuarta proposición.
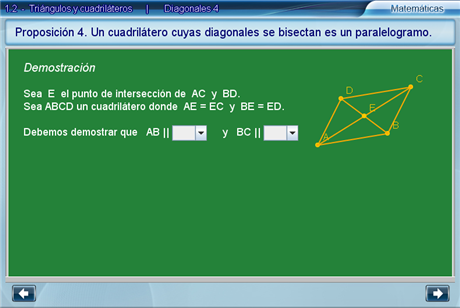
Al final, se tiene la argumentación completa en pantalla.

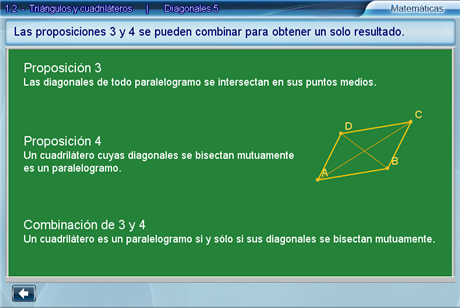
Diagonales 5
Como conclusión, se muestra la forma de combinar las proposiciones 3 y 4 en un solo resultado.
Sugerencias didácticas
-
En cada escena lea las instrucciones en voz alta y cerciórese de que quede claro el objetivo buscado.
-
Realice varios ejemplos y haga notar que en el esquema final no es determinante la forma del paralelogramo para llegar al resultado.
-
Si lo considera apropiado, puede mencionar que el resultado nos da una caracterización de los paralelogramos.
Créditos
Autor
Carlos Alberto Serrato Hernández
Colaboraciones
La unidad fue desarrollada con la colaboración y asesoría técnica de José Luis Abreu León.
Agradecimientos
A Deyanira Monroy Zariñán por su orientación pedagógica.
A Paloma Zubieta López por su apoyo en la redacción.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes y el equipo de MATEMÁTICAS III.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)

