Unidad 5.3Solución de un sistema de ecuaciones como intersección de rectasReferencia curricularPropósito
Instrucciones generalesLa unidad se divide en tres apartados: 1. Movimiento Rectilíneo
2. ¿Tiene solución? 3. Ejercicios Se puede navegar entre los apartados (grupos de
escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
Uso de campos de textoEn algunas escenas aparecen campos de texto para que el usuario escriba en ellos valores o expresiones numéricas. La forma de uso de estos campos es la siguiente:
Uso de calculadoraAl hacer doble clic en un campo de texto o en una de las celdas de una tabla aparecerá una calculadora o un teclado virtual.
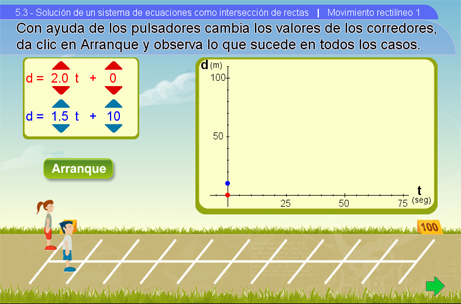
En ambos casos al terminar de introducir los datos se debe presionar el botón Aceptar; en este momento desaparecerá la calculadora y aparecerá el último resultado escrito en ella. 1. Movimiento RectilíneoEste apartado se divide en dos escenas, en las cuales se explica el método gráfico para encontrar la solución de un sistema de dos ecuaciones con dos incógnitas. Movimiento Rectilíneo 1 Esta escena tiene como objetivo explicarle al alumno la posición inicial de un objeto, en este caso, del corredor, y su relación directa con la ecuación de distancia: d=vt+do. Donde v es la velocidad, t el tiempo, d la distancia y do la posición inicial o ventaja que puede tener un corredor con respecto a otro. Las unidades que manejamos en este caso son los metros (m) y los segundos (seg). Al inicio les proponemos un ejercicio determinado, pero si se desea se pueden mover los pulsadores de las ecuaciones roja y azul: los primeros corresponden a la velocidad, la cual puede variar de 1 a 2.5 m/seg; los que siguen son la posición inicial del corredor, los cuales pueden tomar valores de 0 a 50 m. Se le da clic al botón Arranque para que comience la animación y al botón Reiniciar para que la animación se detenga y aparezca otro ejercicio.
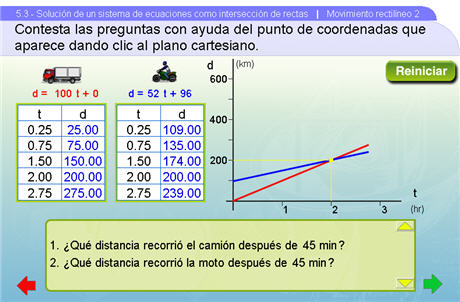
Movimiento Rectilíneo 2 Una vez que el alumno comprende la ecuación de distancia y su relación con la ventaja, entonces podemos empezar a resolver sistemas de ecuaciones por el método gráfico. En esta escena se plantean 6 rutas distintas de carreteras de México, que podemos ver dando clic al botón Otra. En cada una de estas rutas aparecerán la moto o el camión en algún punto fuera de la ciudad origen. Estos datos son importantes para llenar los campos de texto de las ecuaciones presentadas. Lo que estamos pidiendo entonces que llenen es exactamente la ventaja de la que hablamos en la primera escena. Una vez hecho esto damos clic en el botón Verificar para comprobar los resultados.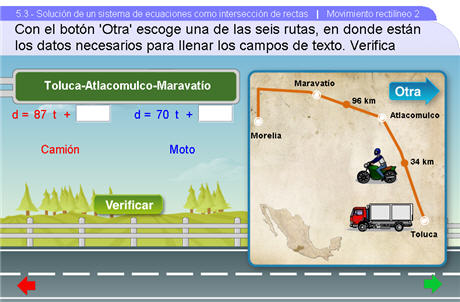
Sugerencias didácticasAntes de empezar con estas escenas es importante recordarle al alumno la ecuación de distancia d=vt, de donde sale y para que nos sirve, de tal forma que no se le dificulte entender el concepto. En la primera escena ya se le puede ir cuestionando al alumno cosas como: ¿Que pasa en la gráfica cuando los corredores se encuentran en determinado momento? ¿Y si ambos van a la misma velocidad y se encuentran en la misma posición?, ¿Si ambos van a la misma velocidad y se encuentran en distintas posiciones? En el caso de que las ecuaciones tengan la misma pendiente y ventaja, la escena explica que la recta graficada no es única, sino que está formada por dos rectas sobrepuestas. Antes de comenzar la escena de Movimiento Rectilíneo 2, es importante recordarles un poco sobre el tema de conversión de unidades, ya que en la etapa de preguntas deben utilizar la conversión de horas a minutos y viceversa. 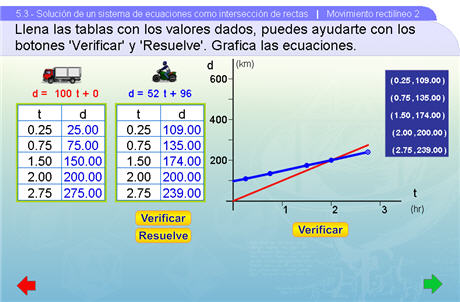El arrastre de los puntos es mucho más fácil con ayuda de las coordenadas escritas del lado derecho de la gráfica. Por lo que se recomienda hacer uso de ellas. Sin embargo, se darán cuenta que el mismo interactivo les ayuda a llegar adecuadamente al punto requerido. Para contestar las preguntas, lo único que se tiene que hacer es arrastrar el punto de coordenadas que se proporciona dentro del plano cartesiano, por lo que se le dejará al profesor la revisión de las respuestas. Se recomienda encontrar primero el valor del tiempo o de la distancia que preguntan, de ahí arrastrar las coordenadas hasta las rectas azul y roja, de esta forma les resultará mucho más fácil encontrar las soluciones. Una vez que el alumno entiende este método se le puede preguntar la solución del sistema por alguno de los otros métodos vistos en la Unidad 05 01, para que compare no solo la facilidad que pueden tener sobre alguno u otro método sino para que vean que la solución es exactamente la misma. 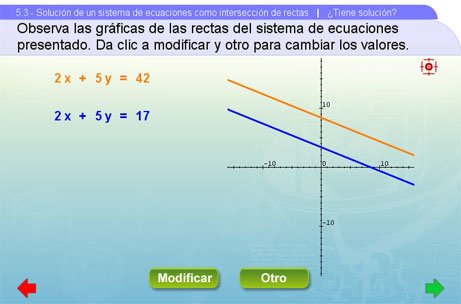2. ¿Tiene solución?Este apartado consta de una sola escena, en la que se pretende mostrar que se puede tener una única solución, una infinidad de soluciones o ninguna. Con el botón Otro irán apareciendo distintos pares de ecuaciones con las gráficas de sus rectas, cada uno de ellos corresponderá a los tres casos mencionados. En cada caso se harán preguntas que ayuden a entender cuando van a existir las soluciones y cuántas se tendrán. Si se quieren cambiar los valores de las ecuaciones entonces dar clic al botón Modificar.
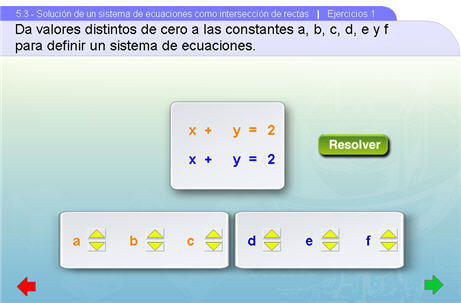
Sugerencias didácticas.Se recomienda que el profesor realice el análisis adecuado en cada caso, contestando las preguntas dadas y proponiendo él mismo sus propios ejercicios además de los que se presentan. 3. EjerciciosEjercicios 1 En esta primera escena se le da al profesor la libertad de elegir el sistema de ecuaciones que pretenda resolver con una única restricción, que los 6 valores presentes (a,b,c,d,e,f) sean distintos de cero. Como se puede observar en la siguiente figura, se deben utilizar los pulsadores para elegir el sistema de ecuaciones y después se debe dar clic al botón Resolver.
Para comenzar a resolver el sistema de ecuaciones, se deben obtener dos coordenadas (x,y) que satisfagan la primera ecuación, de tal forma que podamos graficar la primera recta.
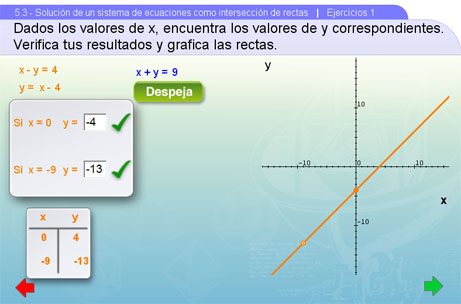
Una vez hecho esto, repetimos el proceso anterior para encontrar dos coordenadas que correspondan a la segunda ecuación. Al terminar, damos clic al botón Preguntas.
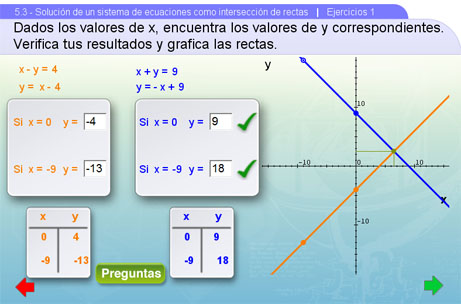
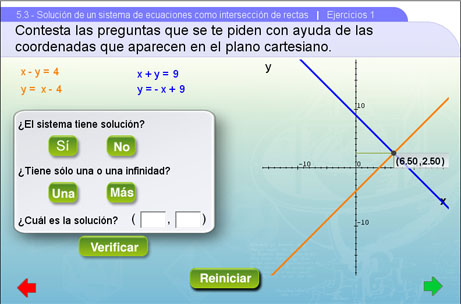
Ya que tenemos la gráfica de las dos rectas que corresponden a las dos ecuaciones, entonces debemos saber si el sistema formado por esas ecuaciones tiene o no solución, si la tiene entonces ¿será única? o ¿tendrá una infinidad? Esto se les pregunta a continuación.
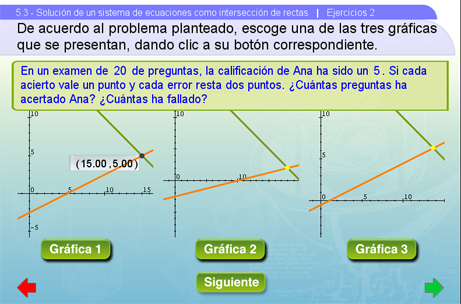
Ejercicios 2 Esta es una escena de ejercicios, en donde se propone un problema y se pide escoger la gráfica que contenga la solución correcta al sistema de ecuaciones que lo representa. Para elegir la gráfica se debe dar clic al botón correspondiente, si está mal, aparecerá un tache, si está bien una paloma. Se puede hacer uso del punto de coordenadas que aparece si le damos clic derecho al mouse dentro del plano cartesiano, para localizar el punto de intersección. Con el botón Siguiente se puede avanzar a otro problema.
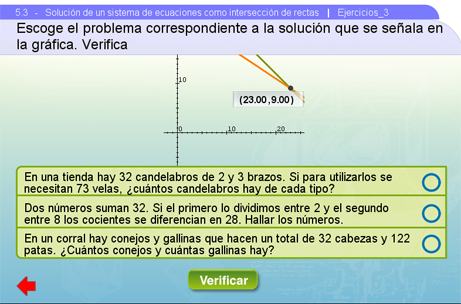
Ejercicios 3 Ahora se da la gráfica de un sistema de ecuaciones y se pide que se escoja el problema que le corresponde, marcando la opción deseada y dando clic al botón Verificar para revisar si es correcta o no. También se puede ver el punto de coordenadas que mencionamos en Ejercicios 2.
Sugerencias didácticasYa que no es fácil conocer la solución del problema viendo la gráfica en una primera instancia, se le debe pedir al alumno, en ambas escenas, encontrar primero el sistema de ecuaciones correspondiente a cada enunciado y después buscar la solución con ayuda del punto de coordenadas que aparece al dar clic derecho al mouse, para conocer el punto de intersección. De esa forma, en Ejercicios 1 se deberán sustituir los valores de x e y de cada uno de los tres puntos de intersección, en las ecuaciones ya obtenidas y al final se darán cuenta que punto es solución. En la segunda escena, los alumnos deberán sustituir el único punto de intersección en los sistemas de ecuaciones obtenidos de los tres problemas. Existen muchos otros ejercicios que pueden darnos resultados interesantes al momento de que el alumno intenta resolverlos, como ejemplo propondré uno de ellos para que se lleven a cabo en clase. Este consiste en darle al alumno una pareja ordenada cualquiera (x=5,y=-2) y dejarle que escriba un sistema de dos ecuaciones con dos incógnitas que tengan como solución este punto del plano cartesiano. Una vez hecho esto, el alumno incluso puede inventarse el problema del cual provienen dichas ecuaciones. El proceso inverso también es interesante: que el alumno proponga un problema, lo desarrolle y observe que debe tener mucho cuidado con los resultados que obtenga, ya que muchas veces éstos pueden ser negativos y pueden no corresponder a las variables reales que estamos manejando (el tiempo, la edad, etc.). Créditos
Autora Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
Brinda acceso a la ayuda de
las escenas interactivas
éste tendrá la misma función que presionar la tecla Intro.
