Unidad 5.2
Movimientos en el Plano
Referencia curricular
Propósito
Que el alumno amplíe su noción de simetría, determine las propiedades de los diferentes tipos aquí expuestos (axial, central y de traslación), y que construya creativamente diseños que combinen los conceptos aprendidos. Asimismo, que se discuta en clase el cómo se aplican los modelos matemáticos a la realidad.
Instrucciones Generales
Esta unidad contiene cinco apartados:
- Dibujo
- Propiedades
- Simetrías
- Realidad
- TANGRAM


Brinda acceso a la ayuda de las escenas interactivas
1. Dibujo
El
apartado Dibujo permite experimentar las
simetrías de forma creativa, dibujando en un espacio que cuenta
con una o dos simetrías axiales, o con una central.
En la segunda sección de esta actividad se puede explorar la
simetría de traslación en
un mosaico, junto con las anteriores.
Dibujo 1
Oprime el botón Demo para ver un video explicativo
sobre las herramientas de esta escena. En
el área blanca es
posible pintar directamente con el dedo, no
es correcto utilizar los plumones del pizarrón
electrónico para este apartado, con ellos no se activa el
programa.
Los botones de esta escena
son:
- Dibujo Libre: Permite pintar libremente sin simetrías.
- Un eje: Permite pintar en el área
blanca con simetría
axial de un eje.
- Dos ejes: Permite
pintar en el área blanca con simetría axial de dos ejes
perpendiculares.
- Punto: Permite pintar en el área blanca con simetría central.
-
Mover ejes: Cuando están seleccionados los ejes, coloca un control de rondana que permite girar los ejes a otra posición. Para girarlos sólo hay que arrastrar el aro rojo hasta llegar a la posición deseada. (En esta escena no es posible trasladar los ejes, solo rotarlos)
- Limpiar: Borra el dibujo creado.
Sugerencias didácticas
El apartado Dibujo está diseñado para mejorar la experiencia de los alumnos con dos tipos de simetrías axiales y con la simetría central. Asimismo introduce el concepto de simetría de traslación. (En algunas partes puede referirse a esta simetría como simetría traslacional)
Esta actividad está sugerida para explicar las definiciones de la unidad. Puede seguirse el siguiente guión de clase:
-
Recuérdese la simetría axial con un eje, vista en primero de secundaria, pintando algo en el área blanca.
-
Utilizando el botón "Dos ejes" muéstrese que esta simetría puede enriquecerse. Se puede comenzar dibujando unos cuantos puntos en la pantalla a la vez que los alumnos intentan describir con palabras lo que sucede con el punto simétrico que el programa dibuja.
Posteriormente es útil pedirle a los alumnos que den ejemplos de objetos reales que tengan simetría de dos ejes. -
La simetría central se explica de manera similar a la anterior presionando el botón Punto y dibujando algo en el área blanca.
Una vez terminada la descripción puede hacerse una demostración utilizando todas las herramientas como la siguiente.
Primero, utilizando 2 ejes dibujamos un caparazón de tortuga y sus patas. Pueden girarse los ejes para un mayor atractivo visual.
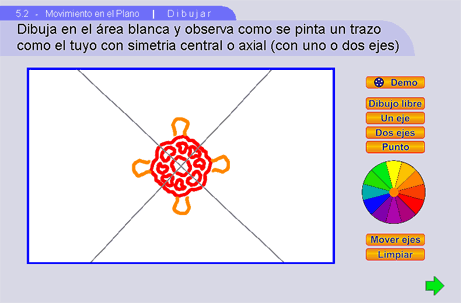
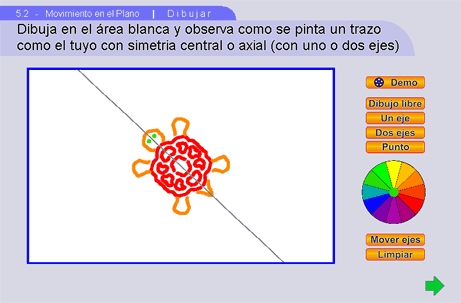
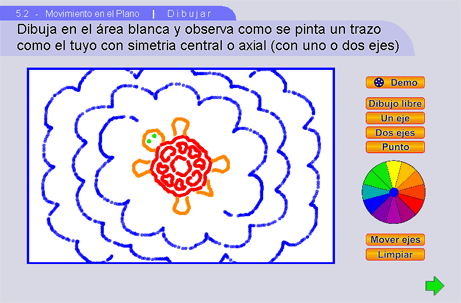
Presionando la flecha verde se pasa a la escena siguiente donde los alumnos pueden experimentar la simetría de traslación.
Nota: El concepto de simetría entendido aquí es, dado un movimiento del plano al que llamaremos simetría, diremos que un objeto determinado es simétrico con respecto a tal movimiento, si al aplicárselo, se ve igual. (En general en vez de movimientos se habla de transformaciones).
Dibujo 2
Oprima
el botón Demo para ver
un video explicativo sobre las
herramientas de esta escena. En el área blanca es posible
pintar directamente con el dedo, no se
utilicen los plumones del pizarrón electrónico para este
apartado, con ellos no se activa el programa.
Los botones de esta escena
son:
- Patrón 1: Activa el área blanca para que el dibujo pintado en el interior del cuadrado se traslade horizontalmente y verticalmente.
- Patrón 2: Activa el área blanca para que el dibujo pintado en el interior del cuadrado se traslade horizontalmente y se refleje verticalmente.
- Patrón 3: Activa el área blanca para que el dibujo pintado en el interior del cuadrado se refleje horizontalmente y verticalmente.
- Retícula: Muestra una cuadrícula que permite entender un poco más que sucede con la simetría.
- Limpiar: Limpia el área blanca.
Puede escogerse el color con el que se pinta tocándolo en el círculo cromático.
Sugerencias didácticas
Los alumnos pueden diseñar un mosaico cuadrado con trazos simples en su cuaderno (los trazos con plumón o crayola en un cuadrado de 5 cm de lado son suficientemente simples para imitar el funcionamiento del programa), al finalizar, se puede escoger a 3 de ellos para que pasen a dibujarlo al pizarrón activando uno de los botones de Patrones (pueden usar colores). Los alumnos que pasan a pintar pueden describir al resto de la clase las simetrías que aparecen en pantalla.
Si se imagina que se está viendo un pedazo de un mosaico infinito puede hablarse de simetría de traslación. Imagínese (en el "Patrón 1") que se mueve todo el espacio una unidad a la derecha, encimando cada cuadrado sobre el espacio de su vecino derecho. Este movimiento deja exactamente igual el dibujo. ¿Qué otras simetrías de traslación hay en este "Patrón 1"? ¿y en los demás?
Los alumnos pueden encontrar todas las simetrías (central, axial y de traslación) que se observan en los diferentes patrones.
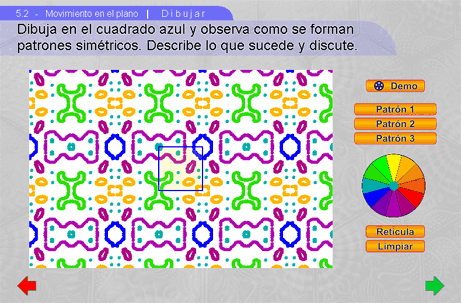
Haciendo equipos, se les puede pedir a los alumnos que diseñen en su cuaderno una pieza cuadrada con las siguientes propiedades:
- No debe haber círculos pintados en la pieza.
- Al armar el mosaico, como en Patrón 1 deben aparecer círculos.
Verifíquense algunas respuestas utilizando el programa. Repetir el ejercicio utilizando los otros 2 patrones.
Otra
posible actividad extra es dejar de tarea el dibujar un mosaico
armado como ellos quieran, pero que cumpla alguna simetría como
las vistas en clase. Se escoge el dibujo más bonito
para que su autor pase al frente y explique las simetrías que
utilizó. Los demás alumnos escriben atrás de su
dibujo las simetrías que usaron antes de la entrega.
2. Propiedades
El
apartado
Propiedades nos permite explorar las características de
la reflexión (simetría axial), la traslación
(simetría de traslación) y la rotación (la simetría central es un
caso particular cuando el ángulo de rotación es de
180°) de figuras geométricas simples. Se
recomienda utilizar este apartado para ejemplificar las definiciones
sobre los diferentes movimientos en el plano y para aclarar la
definición de simetría. El maestro puede utilizar
también esta actividad para comenzar a explorar la
composición de simetrías.
Nota: De acuerdo a la definición
utilizada, dada una transformación del plano, decimos que una determinada figura es simétrica
con respecto a esa transformación si, al aplicarla a la figura,
ésta queda prácticamente igual.
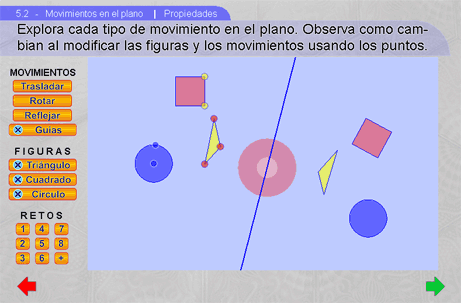
Instrucciones
Pueden modificarse las figuras mostradas en pantalla moviendo los círculos que las definen. Igualmente los movimientos tienen sus correspondientes controles circulares.
Los botones de esta escena son los siguientes:
-
Trasladar: Activa la flecha para trasladar las figuras que se muestran en pantalla. Ésta puede editarse moviendo sus extremos.
-
Rotar: Activa el ángulo de rotación para rotar las figuras que se muestren en pantalla con respecto al centro del control. Puede moverse el centro de rotación y modificarse el ángulo moviendo los círculos correspondientes.
-
Reflejar: Activa la recta de reflexión, la cual puede moverse arrastrando el centro del control (círculo rosa), y girarse, arrastrando la perilla (aro rojo).
-
Guías: Muestra u oculta rectas y arcos que permiten entender mejor la rotación y la traslación.
- Los botones en el menú Figuras muestran u ocultan las diferentes figuras de la escena.
-
Los botones del menú Retos proponen diferentes retos para realizar con las herramientas de la escena. El botón + da varias actividades para que los estudiantes trabajen en sus cuadernos.
Sugerencias didácticas
Después de explorar cada simetría se recomienda resolver en equipos los diferentes retos que aparecen en la escena. Las respuestas deben ser escritas para que el alumno verbalice las ideas matemáticas que va desarrollando.
Al finalizar los 8 retos se pueden resolver los problemas que aparecen en el botón +, ya sea de tarea o en clase, de forma individual o en equipo.
3. Simetrías
Instrucciones
Utilizando los botones se seleccionan las simetrías que posee la figura mostrada. Pulsando el botón Verificar se comprueba la respuesta seleccionada.
Sugerencias didácticas
Este apartado sirve para poner en práctica las definiciones sobre simetría axial, central y de rotación de una figura dada. Se recomienda dejar que los alumnos discutan cuál es la respuesta correcta mientras el profesor simplemente sigue las instrucciones que estos le den. Esta escena es, en particular, muy buena para detectar definiciones mal aprendidas.
Para ilustrar mejor las instrucciones que dan los alumnos sobre los centros o ejes de simetría es conveniente pintarlos con los plumones del pizarrón electrónico, ya que no alteran las funciones del programa y aclaran ampliamente los conceptos aprendidos.

4. Realidad
El
apartado Realidad nos permite identificar
simetrías sobre objetos reales. Esta actividad es especial para ampliar
la discusión sobre la aplicación de modelos matemáticos
al mundo real.
Al
presionar los distintos botones se pueden distinguir simetrías
diferentes. Se
puede cambiar la imagen apretando el botón Siguiente
Imagen.

Sugerencias didácticas
En el apartado Realidad se muestran varios ejemplos del mundo actual. Se sugiere pedir a los alumnos que pinten los ejes y centros de simetría con el plumón del pizarrón electrónico antes de comprobarlos con los botones.
La parte más interesante de esta actividad es comentar como se aplican las estructuras matemáticas a la realidad, que significa aproximar el mundo mediante estructuras y cuales son los beneficios que obtenemos mediante estas aproximaciones.
Un posible comienzo para este ejercicio es darse cuenta de que si uno se fija en muchos detalles de una figura del mundo real ésta “deja” de ser simétrica. Es decir que uno adapta una estructura matemática según las propiedades del objeto estudiado que a uno le interesan. Por ejemplo, si uno quiere cubrir una pared con mosaicos hexagonales que sea durable y resistente, no importa que dibujo tenga cada mosaico. Pero si el objetivo es que sea atractiva a la vista, entonces podría ser de utilidad el fijarse en este detalle.
5. TANGRAM
5. TANGRAM
El
apartado TANGRAM está diseñado para favorecer
ampliamente las habilidades para identificar desarrollos
simétricos mediante este divertido juego.
Instrucciones
Para armar la figura que se seleccione de la parte inferior, hay que mover los TANS (pedazos del TANGRAM) con el control de rondana usado en el apartado Propiedades.
Sugerencias didácticas
La última actividad se dedica al antiguo juego chino del TANGRAM. Esta actividad es ampliamente recomendada para obtener un aprendizaje sólido sobre la manipulación de figuras utilizando “movimientos en el plano”. Con ella se refuerzan los conceptos de simetría axial y de rotación de una forma no convencional; ya que, para llegar a obtener una figura simétrica dada, se tienen que pasar por un proceso laborioso pero divertido. Los alumnos apreciarán más el resultado obtenido y la aplicación de las definiciones adquiridas en clase.
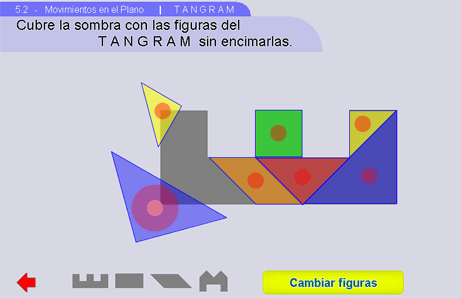
Es ampliamente recomendable apoyar esta actividad con TANGRAMS de papel. Éstos pueden hacer con hojas de cuaderno en clase imitando el TANGRAM armado en forma de cuadrado que aparece en esta actividad. Cada vez que se escoja un reto en el apartado se les propone a los alumnos el realizarlo. Cuando un alumno lo haya conseguido, se le pasa al pizarrón electrónico para que muestre su solución moviendo las piezas del cuadrado.
Datos curiosos sobre las simetrías:
-
Las simetrías son de gran utilidad al estudiar las estructuras microscópicas de los cristales, como la de los cuarzos, los diamantes, los zafiros, la sal, el hielo, los rubíes, etc.
(Por ejemplo se puede distinguir entre una zirconia y un diamante viendo la diferencia que existe entre la simetrías de sus reflejos, los diamantes para conservar su peso, se cortan de forma irregular, lo cual distorsiona los reflejos que tiene sobre el. Para distinguir un zafiro estrella real de uno falso que iguale el color se observa la bella simetría hexagonal que estos producen, las imitaciones baratas generalmente no la tienen). Nota: Las zirconias son también conocido con el nombre de circones y son utilizados en la joyería para imitar diamantes. -
Las simetrías se utilizan para calcular los movimientos de algunas máquinas, como por ejemplo las ruedas de la fortuna.
-
Las galaxias espiral se clasifican de acuerdo a su simetrías de rotación.
-
En la industria textil, las simetrías se utilizan para crear bellos dibujos que, por repetir el mismo patrón, se producen de forma sencilla reduciendo costos.
-
En ingeniería, las estructuras simétricas, en general son más estables que las no simétricas (imagina una llanta de auto que no tenga los tornillos acomodados simétricamente, por ejemplo amontonados todos en un solo lugar).
-
Los árabes reprodujeron todos los grupos de simetrías del plano en diferentes obras artísticas hace ya varios siglos antes de que se comenzaran a estudiar en occidente. Pueden verse casi todas los posibles grupos de simetría en La Alhambra, ubicada en Granada, España.
-
La naturaleza tiene una gran variedad de figuras simétricas. En general, genéticamente es más fácil dar instrucciones para que se forme un ser "simétrico" a darlas para formar uno que no lo sea. Este fenómeno se estudia en Morfogénesis y en formación de patrones.
Créditos
Autor
Claudio Francisco Nebbia Rubio
Agradecimientos
A Julio Arnoldo Prado Saavedra y a Oscar Escamilla González,
integrantes del Grupo Descartes, por sus ideas y apoyo en la
realización de esta unidad.
Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)