Unidad 4.3Rectas y puntos notables del triánguloReferencia curricularPropósitoPresentar las rectas y puntos notables de los triángulos y estudiar sus propiedades. Instrucciones GeneralesEsta unidad tiene cuatro apartados cada uno de ellos con dos escenas: 1. Mediatrices
Se puede navegar entre los apartados o escenas con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
1. MediatricesEsta sección tiene dos escenas cada una con varios pasos. La primera escena presenta un recordatorio del método para construir una mediatriz usando regla y compás. En el último paso se muestra que las tres mediatrices de un triángulo se intersecan en un punto.
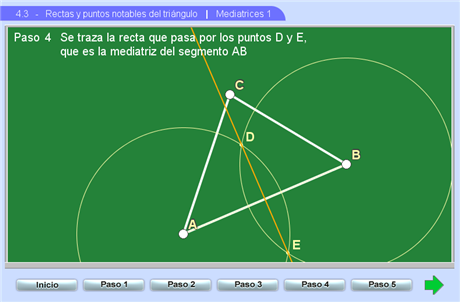
La segunda escena está encaminada a explorar argumentos sencillos que explican porqué las mediatrices pasan por un punto y que éste se llama circuncentro por ser el centro de la circunferencia que pasa por los tres vértices del triángulo.
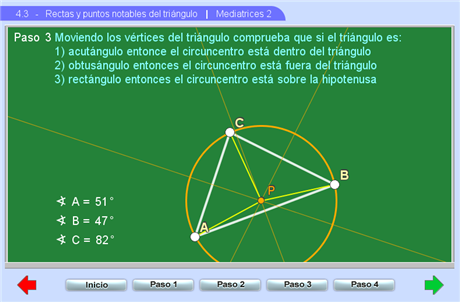
Posteriormente explora dónde se localiza dicho punto en los distintos tipos de triángulos: acutángulos, obtusángulos y rectángulos. Sugerencias didácticas.Conviene seguir cada uno de los pasos de las escenas y siempre hacer cambios en el triángulo arrastrando sus vértices. Este proceso debe llevar al alumno a darse cuenta de que la propiedad de que las mediatrices convergen en un punto no es una casualidad sino que obedece a una razón profunda y completamente general. En la segunda escena, conviene detenerse y concentrarse en el paso 1. Conviene encaminar la discusión en clase de manera que los alumnos completen el siguiente argumento: 1) Los puntos que equidistan de dos vértices del triángulo están sobre la mediatriz del lado correspondiente. 2) Por tanto la intersección de dos mediatrices equidista de los tres vértices. 3) Por tanto la otra mediatriz debe pasar por el mismo punto. 4) Así mismo, el punto de intersección de las mediatrices es el centro de la circunferencia que pasa por los tres vértices del triángulo, que se llama la circunferencia circunscrita. Finalmente, conviene mostrar que el nombre de circuncentro viene precisamente de ser el centro de la circunferencia circunscrita.
2. AlturasEste apartado tiene dos escena. La primera hace un repaso del concepto de altura en un triángulo y su uso en el cálculo del área. Se intenta hacer ver a los alumnos que cualquier lado de un triángulo puede tomarse como base y que la altura que le corresponde si se quiere obtener el área es la que es perpendicular a ese lado y pasa por el vértice opuesto.
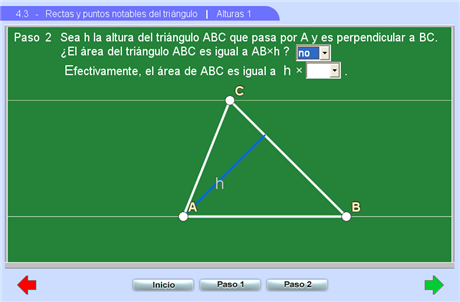
La segunda escena está diseñada para que el estudiante observe que las tres alturas de un triángulo pasan por un punto, al cual se le llama ortocentro y a explorar su localización en los distintos tipos de triángulos.
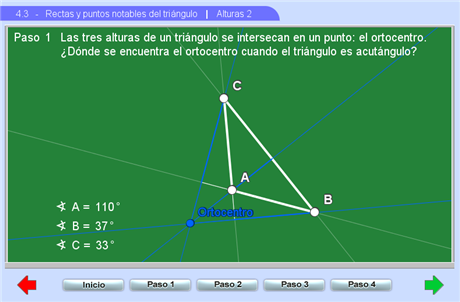
Sugerencias didácticasLa demostración de que las alturas de un triángulo convergen en un punto está fuera del alcance del segundo de secundaria, por tanto no conviene intentar llegar a una demostración. Por ello estas escenas se centran en otros objetivos. En la primera escena se encamina a aclarar la confusión que suele haber en muchos alumnos de creer que la base de un triángulo es el lado horizontal (o el más horizontal) y la altura es sólo la correspondiente al vértice que está más arriba. Se sugiere al maestro centrar la atención de los alumnos en convencerse de que para calcular el área de un triángulo, puede usarse cualquiera de sus alturas, pero que una vez elegina la altura es necesario usar lcomo base el lado perpendicular a esa altura. La segunda escena puede enfocarse alrededor del aparentemente curioso hecho de que en un triángulo rectángulo el ortocentro coincide con el vértice del ángulo recto. En realidad es un hecho muy fácil de demostrar: los catetos de un triángulo rectángulo son dos alturas del triángulo, por tanto se intersecan en el vértice donde se unen, que es el del ángulo recto. Éste último es un argumento riguroso y simple que conviene que los alumnos construyan con ayuda del maestro. 3. MedianasEste apartado consta de dos escenas. La primera está destinada a llevar al estudiante a descubrir que también las medianas de un triángulo se intersecan en un punto, el cual se llama el baricentro. De paso se hace patente el hecho de que una mediana parte al triángulo en dos con la misma área.
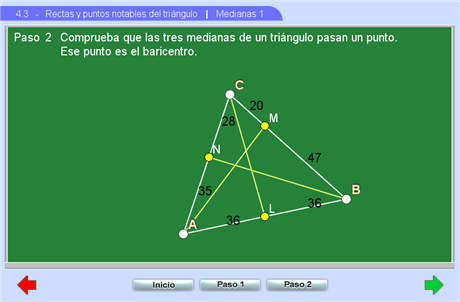
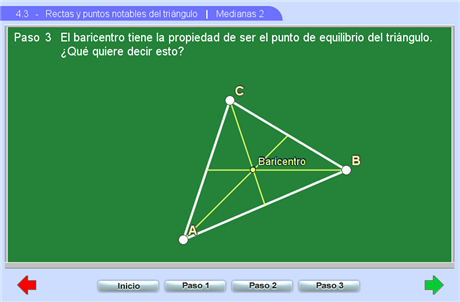
La segunda escena explora las propiedades del baricentro como punto de equilibrio del triángulo.
Sugerencias didácticasA pesar de que las medianas son quizás las rectas notables más fáciles de reconocer, no es fácil demostrar que convergen en un punto. No se pretende dar una demostración en estas escenas, sólo se pretende hacer a los alumnos observar: a) que las medianas parten al triángulo en dos de áreas iguales (esto puede deducirse fácilmente) b) que las medianas convergen en un punto (se puede comprobar experimentando con varios casos). c) que es plausible a simple vista que el punto de intersección es el punto de equilibrio y que es por eso que se llama baricentro, que quiere decir centro de gravedad. Nota: a) no es suficiente para demostrar que la mediana es una recta de equilibrio del triángulo, para ello habría que dar un argumento un poco más profundo, por ejemplo en términos del centro de masa de los segmentos paralelos a un lado que tienen sus extremos en los otros dos lados.
4. BisectricesEste apartado también tiene dos escenas, aunque sólo la primera trata realmente las bisectrices. La primera escena recuerda la construcción de una bisectriz y
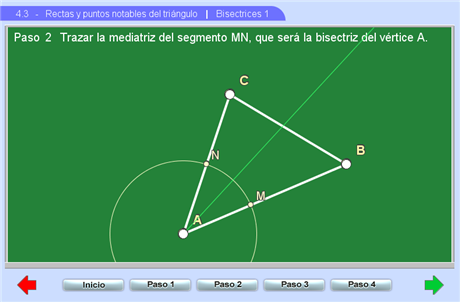
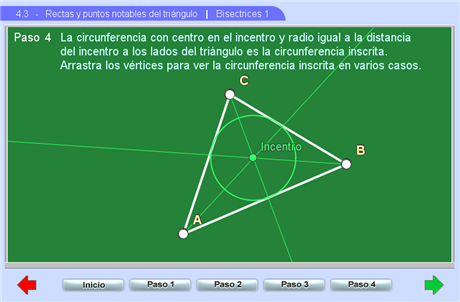
muestra que las tres bisectrices se intersecan en un punto. Se dan argumentos sencillos que explican porqué las bisectrices pasan por un mismo punto y porqué este punto es el centro de la circunferencia inscrita en el triángulo y que es tangente a los tres lados..
5. ResumenLa última escena de la unidad es propiamente un RESUMEN de toda la unidad. Presenta un triángulo dinámico y unos botones con los que se puede elegir que se dibujen o no todas las rectas y puntos notables del triángulo. Con esta escena se pueden explorar las interesantes propiedades de los puntos notables. Hay botones para mostrar la recta de Euler, que es la que une al ortocentro con el circuncentro y que incluye al baricentro.
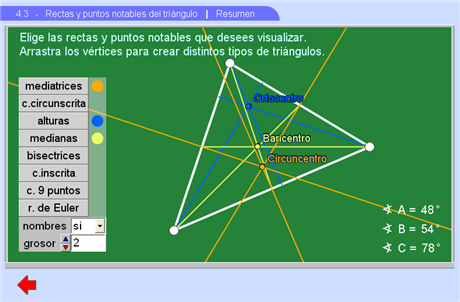
También hay un botón para mostrar la llamada circunferencia de los nueve puntos que pasa por los pies de las alturas, por los puntos medios de los lados y por los puntos medios de los segmentos que unen los vértices con el ortocentro. Sugerencias didácticasLa primera escena se puede usar para dar una demostración de que las bisectrices convergen en un punto. Las líneas de la demostración son más o menos éstas: 1) Los puntos sobre la bisectiz son los que equidistan de los lados adyacentes. (Aquí hay que entender como distancia de un punto a una recta la que se mide sobre la prependicular del punto a la recta) 2) La intersección de dos bisectrices equidista de los trs lados del triángulo. 3) Por tanto, la tercera bisectriz debe pasar por ese mismo punto. Respecto a la segunda escena, se sugiere al maestro explorarla libremente con sus alumnos haciendo mucho movimientos y prendiendo y apagando diferentes conjuntos de rectas notables, induciendo a los alumnos a hacer observaciones y comentarlas en voz alta. Se trata de una escena muy rica en interacción y contenido y muy visual por lo que puede ser un buen atractor de la atención del grupo. Una vez captada la atención del grupo se pueden mostrar primero la recta de Euler y después la circunferencia de los nueve puntos y retar a los alumnos a describir sus propiedades deduciéndolas por pura observación de la escena. Créditos
Autor Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
Brinda acceso a la ayuda de las escenas interactivas
