Unidad 2.7Medidas de tendencia centralReferencia curricularPropósito
Interpretar y calcular las medidas de tendencia central de un conjunto
de datos agrupados, considerando de manera especial las propiedades de
la media aritmética. Instrucciones generalesLa unidad se divide en cuatro apartados : 1. Ejemplos2. Propiedades 3. Gráfica de edades 4. Ejercicios Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
Brinda acceso a la ayuda de las escenas interactivas 1. EjemplosEste apartado se compone de cuatro escenas: 1.1 ¿Cuánto mides?1.2 ¿Cuántos focos? 1.3 ¿Cuánto tiempo? 1.4 ¿Cuántos años? Estas cuatro escenas sirven para recordar la forma de obtener las medidas de tendencia central con datos no agrupados. 1.1 ¿Cuánto mides?La idea de este ejercicio es que un grupo de alumnos (máximo 12) escriban su estatura, en centímetros. Al apretar el botón Agregar aparecerá un conjunto de flechas verdes (llamadas Pulsadores) que servirán para introducir los datos. Las flechas individuales de la derecha aumentan (las de la izquierda disminuyen) de uno en uno, mientras que las dobles lo hacen de diez en diez. Por ejemplo, una manera de escribir 84 es apretar 8 veces la doble flecha derecha y 4 veces la flecha sencilla derecha. También se puede escribir 90 y luego restar 6 con la flecha izquierda.
La flecha verde que está abajo a la derecha sirve para avanzar a la siguiente escena de la unidad interactiva. Cuando haya una flecha roja en la parte inferior e izquierda de la pantalla, ésta servirá para regresar a la escena anterior. 1.2 ¿Cuántos focos?¿Hay en tu casa? De manera similar al ejercicio anterior se trata de que un grupo de alumnos (12 máximo) diga cuantos focos hay en su casa. Pídales que piensen desde la entrada de su casa, la cocina, recamara y baño, que mentalmente recorran ordenadamente su casa y memoricen el número de focos, sin olvidar lámparas de mesa o de piso, y una vez seguros, introduzcan los datos en el programa. La siguiente imagen aparece después de introducir 5 datos y apretar el botón Listo, en ella se muestra la Mediana del conjunto de números.
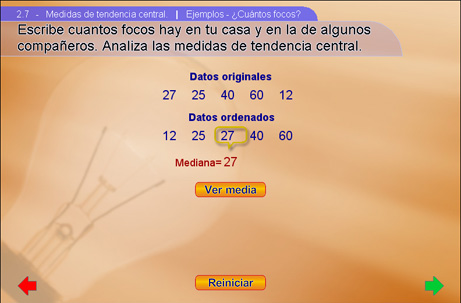
1.3 ¿Cuánto tiempo?¿Tardas en llegar a la escuela? Se trata de que a lo más 12 alumnos digan cuánto les lleva el recorrido en minutos, e ingresar los números como en los casos anteriores. Por ser tan similar a las dos primeras situaciones, esa escena no se muestra. 1.4 ¿Cuántos años?¿Cuántos años tiene tu abuelita? Tal vez no te quiera decir, pero pregúntale al abuelo y a lo mejor te dice. Si no es posible, se trata que los alumnos especulen e ingresen los datos para obtener resultados similares a los siguientes, donde se aprecian Mediana, Media y Moda.
En estas escenas es posible calcular las medidas de tendencia central paso a paso.
Al presionar el botón Listo debajo del texto Datos originales aparecerán los datos en el orden en que fueron introducidos. Después aparecerá un nuevo botón con la leyenda Ver Mediana. Al presionarlo aparecerán los datos ordenados de menor a mayor. Este orden facilita encontrar la mediana, que es el dato central si el número de datos es impar. En el caso de que el número de datos sea par, la mediana se calculará como el promedio de los dos datos centrales. En las imágenes anteriores de las escenas ¿Cuántos focos? y ¿Cuántos años? se ejemplifican ambos casos. 2. PropiedadesEste apartado consta de tres escenas. Propiedades 1Aparecen cinco figuras humanas y se le pide a algún alumno que, con ayuda de los pulsadores (las flechas azules) haga crecer cada figura hasta obtener la estatura de cinco compañeros. El rango de alturas disponible es de un metro a uno noventa.
La imagen anterior muestra una propiedad de la media, que dice que la suma de las diferencias de cada uno de los datos con respecto a la media es igual a cero y puede entenderse de la siguiente manera: La altura que a algunos les falta para alcanzar la media, es la altura que a otros les sobra Esta propiedad puede comprobarse al sumar cada una de las cantidades que se encuentran dentro de los globos. El signo positivo o negativo hace referencia a si tiene una cantidad "de más" o "de menos" respecto a la media. Al terminar, el alumno participante tendrá la opción de presionar el botón que está del lado izquierdo para ver el valor de la media de las estaturas. Propiedades 2
La
mediana es aquél número que divide al conjunto de datos en dos grupos
del mismo tamaño. Un grupo contendrá todos los valores que son menores
que la mediana y el otro todos los que son mayores.
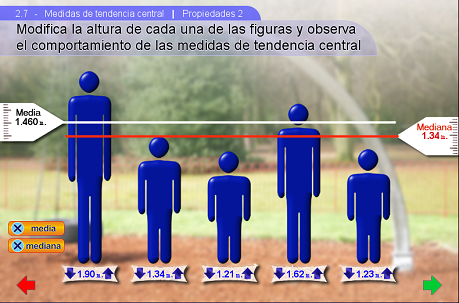
En nuestro ejemplo, la mediana es la altura de la figura para la que hay dos figuras más altas y dos más bajas. Propiedades 3 En
esta última escena del apartado pasaremos de datos no agrupados a datos
agrupados y veremos la manera de encontrar las medidas de tendencia
central en ambos casos.
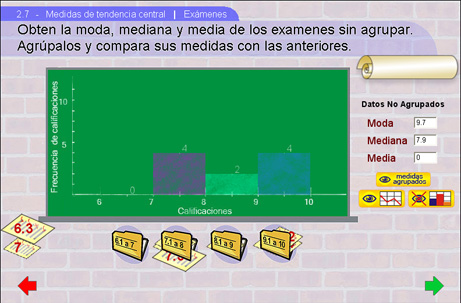
Los datos serán las calificaciones de ciertos exámenes. Primero, se deben ordenar de menor a mayor, para así encontrar la mediana. Usando la calculadora deberán obtener la media y buscar que dato o datos se repiten, para así encontrar la moda. Los valores encontrados se deben colocar en los cuadros de texto de la parte derecha de la pantalla y también en el cuaderno del alumno, esto se hace con el fin de ver que no siempre se obtienen los mismos valores de las medidas de tendencia central cuando los obtenemos a partir de datos no agrupados a cuando lo hacemos con datos agrupados. Después de obtener las medidas, el alumno debe colocar cada uno de los exámenes en la carpeta que le corresponda según la calificación que aparece en el examen; el fin de esto último es agrupar los datos y formar el histograma de dichos datos agrupados. Se recomienda usar el botón Medidas agrupadas para desplegar las medidas de tendencia central de datos agrupados y poder comparar y analizar porqué son diferentes. La idea de poner las carpetas es que los exámenes ya agrupados no son visibles, y por tanto, no sabemos cuales son los datos originales, perdiendo entonces información al agrupar. Es por ello que son distintos.
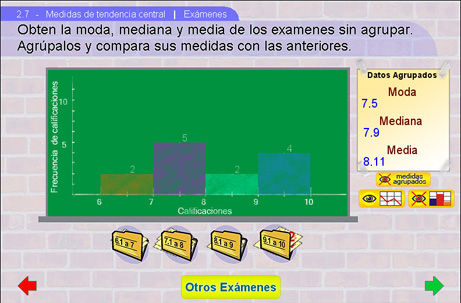
Sugerencias didácticas.En la prática suele suceder que se tenga que elegir entre las medidas de tendencia central para representar a un conjunto de datos, es importante hacer notar que no hay una receta mágica para ello, siempre va a depender del contexto y de lo que se busque para poder hacer una mejor elección. Deje muy claro que las escenas 1.5 y 1.6 NO PRESENTAN UN HISTOGRAMA, y que no traten de verlo como una gráfica, simplemente es una representación de las estaturas de 5 jóvenes, y que en caso de querer graficar el histograma, primero tendrían que agrupar los datos. 3. Gráfica de edades.Este apartado cuenta con dos escenas con datos agrupados. Gráfica de edades 1 y Gráfica de edades 2. Gráfica de edades 1 En
la primera imagen de este apartado, se aprecia un histograma con
frecuencias de edades entre los 7 y 17 años y el objeto, es encontrar
la mediana.
Para esto algún alumno elegido deberá mover el diamante negro -colocado abajo del eje X- hasta donde crea que el área total se divide en dos partes iguales. Las ayudas proporcionadas son:
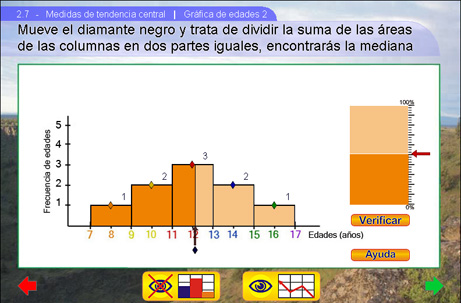
Al apretar el botón Verificar se mostrará exactamente donde está la mediana:
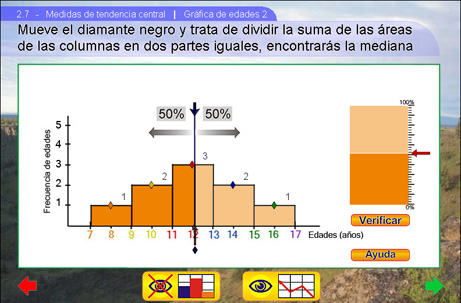
Gráfica de edades 2 La
siguiente y última escena muestra inicialmente el mismo histograma que
el anterior pero con la diferencia de que éste se puede modificar.
La idea principal de este ejemplo es que el alumno identifique la posición de la mediana al cambiar los valores de las columnas. En la parte inferior de la gráfica se encuentran tres flechas, cada una muestra la posición de una medida de tendencia central (Moda, Mediana y Media) . Note dos de los tres casos mostrados en la escena:
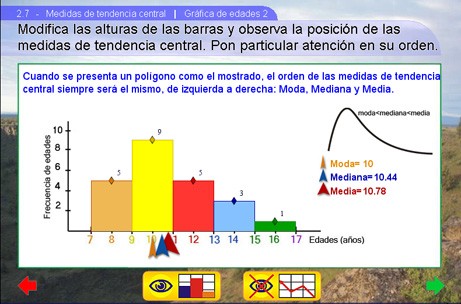
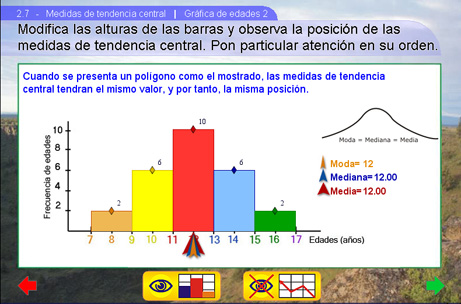
Sugerencias didácticas.Pase al alumno a comprobar que las áreas son proporcionales a la frecuencia de cada columna. Se recomienda que el alumno identifique los tres casos que se muestran en la escena, así como también la relación de la forma de la gráfica con el valor de las medidas de tendencia central. En escenas posteriores será crucial para resolver problemas que implican el cálculo de las medidas de tendencia central. 4. EjerciciosEste último apartado contiene dos escenas: Ejercicios 1 y Ejercicios 2. Ejercicios 1Se
desea que el alumno lea la pregunta que aparece abajo del eje X y
responda correctamente, colocando la flecha en la posición apropiada.
Una vez colocada la flecha, se le pedirá que compruebe su resultado apretando el botón Verificar. Nota: El botón Verificar solo comprueba la respuesta a la pregunta que aparece en pantalla.
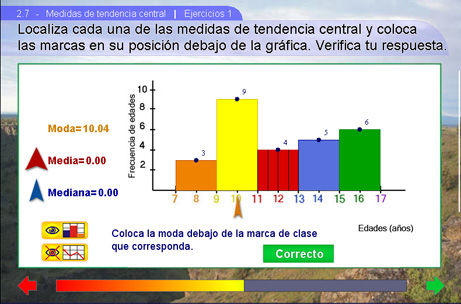
En el caso de la mediana, se muestra como ayuda la retícula en la clase donde se encuentra la mediana, el alumno sólo debe hacer unos cálculos sencillos y en el mejor de los casos bastará contar las observaciones. Es importante mencionar que puede colocar las flechas en un valor aproximado pero debe de ser muy aproximado al valor real de la medida de tendencia central, de lo contrario su respuesta será calificada como incorrecta.
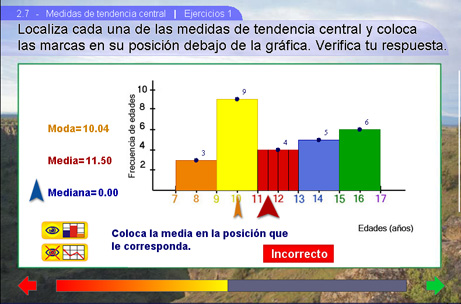
Note la Barra Central en la parte inferior de las imágenes anteriores. La parte coloreada crecerá en caso que la respuesta sea correcta y se encogerá en caso contrario. Existen dos situaciones extremas: Después de contestar acertadamente varias veces, la barra crecerá hasta su máxima longitud y entonces, invitará a pasar a la siguiente escena. En caso contrario, o sea, si se responde erróneamente varias veces, la barra se encogerá hasta desaparecer. Esto significa que no se ha entendido bien el tema y el programa sugerirá regresar al apartado anterior. Ejercicios 2A continuación aparecen dos polígonos de frecuencias y se pide al alumno que los analice y responda las preguntas mostradas abajo del eje X, comprobando su respuesta con el botón Verificar.
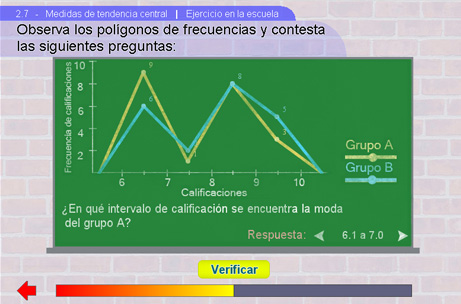
Sugerencias Didácticas.Cuando se pida “Encontrar la Mediana”, recordar a los alumnos que la mediana divide al conjunto de datos en dos grupos. Y, para encontrarla explícita y gráficamente, basta dividir el número de datos entre dos y buscar la clase hasta donde se han acumulado tantas observaciones como ese valor. Por ejemplo, si se tienen 15 datos, la mediana corresponde al valor de la octava observación una vez que se han ordenado. Habrá 7 datos menores que ella y 7 mayores que ella. Para localizarla en un histograma, habrá que buscar las clase que contiene a la octava observación y aproximar su valor en el eje X. Créditos
Autor Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
