Unidad 2.2 aMultiplicación y división de expresiones algebraicasReferencia curricularPropósitoResolver problemas multiplicativos que impliquen el uso de expresiones algebraicas. Instrucciones generalesEn esta sesión el estudiante explorará la multiplicación de expresiones algebraicas a través del modelo geométrico. La unidad se divide en 3 apartados:
1. Adivina
2. Monomios 3. Binomios Se puede navegar entre los apartados (grupos de escenas) con el menú de la parte inferior.
Este menú aparece a lo largo de toda la unidad y conserva su funcionalidad.
1. AdivinaEste apartado consta de 2 escenas. Adivina 1
En esta primera escena, la adivina Merlina invita al estudiante a participar en el juego denominado
Adivina 2En esta escena se muestra el método algebraico que Merlina siguió. Esto sirve como una introducción a la manipulación de expresiones algebraicas. La forma de interacción es de nuevo a través de la operación de presionar un botón.
Sugerencias didácticasSe sugiere usar el apartado la Adivina como una introducción motivacional que invite al alumno al aprendizaje de las expresiones algebraicas y sus operaciones. 2. MonomiosEl apartado de monomios consta de 2 escenas. Monomios 1En Monomios 1 se le da al estudiante una consigna de exploración basada en la asociación entre área de un rectángulo y multiplicación de monomios. La interacción se realiza a través de pulsadores para variar los coeficientes de la expresión algebraica. Se espera que mediante la exploración interactiva con esta escena, el estudiante se apropie del modelo geométrico para la multiplicación de monomios.
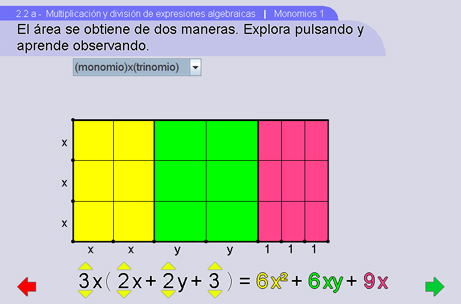
Monomios 2Monomios 2 plantea un ejercicio en el cual se van a usar los principios multiplicativos de la escena anterior. En esta escena, ya no se pone el modelo geométrico. Se le pide al estudiante que realice las operaciones de manera puramente algebraica.
Sugerencias didácticasEl apartado de monomios se puede usar como una introducción a la multiplicación de expresiones algebraicas, antes de iniciar la exposición de la regla distributiva. El objetivo es modesto: que el alumno llegue a multiplicar correctamente dos monomios. 3. BinomiosBinomios 1En Binomios 1 se evalúan dos expresiones algebraicas en uno o más valores de x con el propósito de que el estudiante adquiera la habilidad de distribuir una expresión de la forma a(bx+c). Con los pulsadores el estudiante explora las posibilidades de modificar la expresión algebraica y el valor de la x.
Binomios 2En Binomios 2 se continúa con el modelo de áreas para ver la multiplicación por binomios.
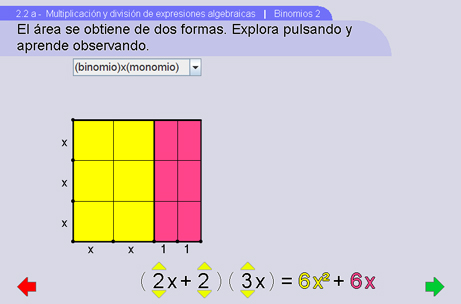
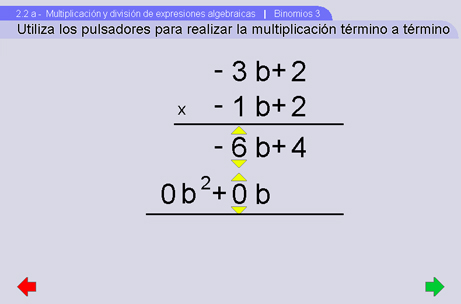
Binomios 3El objetivo de esta escena es mostrar al estudiante una forma de multiplicar binomios. Esta forma asemeja la forma de multiplicar dos números. En esta escena se le ayuda al estudiante (mediante un sombreado intermitente) a que calcule paso a paso el producto de dos binomios. De manera aleatoria se generan dos expresiones. La escena guía al estudiante resaltando los términos que se deberán de multiplicar. Esta escena sólo pretende que los alumnos aprendan a multiplicar binomios y no se debe ver como un ejercicio. Una vez que entiendan la forma de multiplicar los binomios, la escena Binomios 4 presentará ejercicios aleatorios para practicar este algoritmo ya sin ningún tipo de ayuda.
Binomios 4En esta escena ya se le pide al estudiante que calcule el producto de dos binomios. La multiplicación la realiza el estudiante con los pulsadores.
Sugerencias didácticasSe sugiere usar este apartado para que el estudiante practique la ley distributiva de la multiplicación respecto a la suma tantas veces como lo desee hasta llegar a dominarla. Los ultimos dos ejercicios plantea la multiplicación a la manera de la multiplicación común de dos números. El tutor puede poner más ejercicios en donde se vea la equivalencia entre los dos métodos de multiplicar binomios. La distributividad es una regla y como tal el estudiante debe aprender a seguirla al pie de la letra.
Créditos
Autora Esta unidad interactiva fue desarrollada en el ILCE por el Grupo Descartes. Sus contenidos se distribuyen bajo una licencia de  La unidad utiliza Descartes que es software libre. Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
|
Brinda acceso a la ayuda de las escenas interactivas
