Unidad Interactiva 3.1.2
¿Para qué sirven los modelos?
Referencia curricular
Propósito
El interactivo permite que el alumno compare diferentes modelos e identifique sus características.
Instrucciones generales

La unidad consta de una escena.
Escena 1
-
Botón "reiniciar"
Reinicia la escena al estado original.
-
Menú de controles
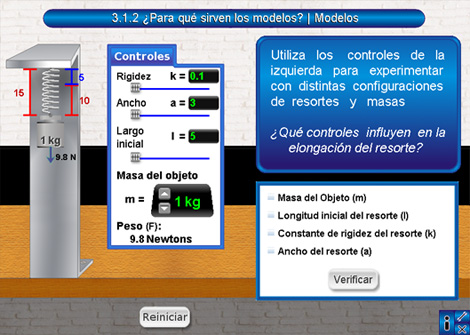
Muestra los controles que permiten modificar y visualizar los parámetros del resorte.
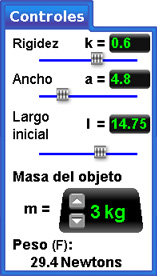
Con los controles se puede variar la masa del objeto que cuelga del resorte, así como la constante de rigidez (k), el ancho (a) y el largo inicial del resorte (l). Al manipular estos datos, aparecen sobre el sistema masa-resorte ubicado del lado izquierdo de la pantalla, los valores de la elongación y la diferencia de longitudes del resorte, así como el peso del objeto colgante. Este último se expresa en Newtons.
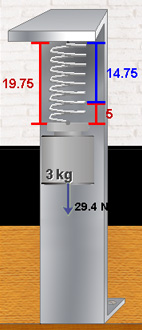
La manipulación de los controles determina el comportamiento del sistema, que es simulado en la animación correspondiente.
-
Opciones a seleccionar
La pantalla de instrucciones indica al usuario qué es lo que debe manipular en la pantalla de controles y el reto que se debe resolver. El reto consiste en identificar las variables que influyen en el comportamiento del sistema, es decir, el modelo matemático que las relaciona para producir el efecto que se observa en cada iteración.

-
Botón "verificar - corregir" Al presionar este botón, el interactivo verifica las opciones seleccionadas. En caso de que no todas las selecciones sean correctas, el botón cambia su etiqueta a
 . Además se muestran en rojo las opciones incorrectas y en verde las correctas.
. Además se muestran en rojo las opciones incorrectas y en verde las correctas. -
Botón "registrar" Después de contestar correctamente la pregunta, aparece una nueva instrucción en la parte superior derecha. Una vez que se ha leído, se presiona el botón "continuar" para realizar el procedimiento que se indica. Se trata de seleccionar valores para la masa del objeto colgante, los cuales se tabulan al presionar la tecla
 . Cada valor aparece automáticamente en la tabla junto con los de las variables k (constante de rigidez) y e
(elongación). Cuando se selecciona un valor de masa que ya ha sido
registrado anteriormente, aparece un texto que indica "ya has
registrado ese valor".
. Cada valor aparece automáticamente en la tabla junto con los de las variables k (constante de rigidez) y e
(elongación). Cuando se selecciona un valor de masa que ya ha sido
registrado anteriormente, aparece un texto que indica "ya has
registrado ese valor". -
Cuando la tabla contiene todos los datos, aparece una gráfica de elongación contra masa y una ventana que describe la relación que guardan estas variables.
- Al continuar con el programa, se muestra una ventana de instrucciones en la que se plantea un procedimiento similar al anterior, en donde el usuario debe manipular la variable k para hacer la tabulación correspondiente.
-
Cuando se han registrado todos los datos, aparece la gráfica correspondiente de elongación contra constante k .
-
La información que el usuario tiene hasta ese momento, le permitirá hacer inferencias para seleccionar la ecuación que modela el comportamiento del sistema. Al presionar en cualquiera de esta expresiones matemáticas, el sistema se animará de acuerdo a la relación que guardan las variables del modelo seleccionado. Al seleccionar la opción correcta, es decir, l = m/k , y se muestra la retroalimentación positiva al respecto.
Sugerencias didácticas
Eje temático: Bloque 3 . Las interacciones de la materia. Un modelo para describir lo que no percibimos.
Tema: 3.1. La diversidad de los objetos.
Subtema: 3.1.2 ¿Para qué sirven los modelos?
Aprendizaje esperado:
- Interpreta y analiza la información que contienen distintos modelos de fenómenos y procesos.
- Reconoce que un modelo es una representación imaginaria y arbitraria de objetos y procesos que incluye reglas de funcionamiento y no la realidad misma.
Destrezas científicas: Comparar las características de algunos modelos.
Conocimientos previos: Segundo de secundaria, Ciencias II, Bloques I y II. A lo largo de estos bloques, los alumnos han estudiado distintas expresiones simbólicas y gráficas que representan fenómenos físicos relacionados con el movimiento, la fuerza y la energía. Las variables que componen estas expresiones se han analizado de manera fenomenológica, de manera que los alumnos pueden reconocer que su variación tiene efectos en el comportamiento de un fenómeno.
Ideas previas: Algunos estudiantes suele pensar equivocadamente que los modelos son únicamente representaciones analógicas de un hecho, fenómeno o proceso, como ocurre en los esquemas, dibujos y maquetas, sin considerar que las teorías científicas son modelos de explicación de la naturaleza cuyo poder reside en el lenguaje matemático, que generalizan los patrones de comportamiento de las variables.
Estrategias didácticas:
1. Permita a los alumnos comenzar la interacción modificando libremente las variables masa del objeto, largo inicial y ancho del resorte. De esta manera se familiarizan con los controles y establecen algunas aproximaciones iniciales sobre la relación que guardan estas magnitudes.
2. Sugiérales observar con atención cómo se comporta el resorte al manipular las variables para que establezcan sus primeras relaciones de causa efecto. Es importante que analicen cómo se modifican los valores en cada interacción.
3. Una vez que los alumnos han seleccionado las variables que intervienen en el fenómeno, se despliegan las expresiones matemáticas que podrían modelar el fenómeno. Es importante que los alumnos reconozcan que las características del modelo permiten que se transforme y someta a diversas valores, pero representa un fenómeno. Las simulaciones de los distintos valores de las mismas variables en las expresiones son una oportunidad para la discusión en el grupo.
5. Se recomienda recordar con los alumnos los conceptos de variación proporcional inversa y directa para encontrar la lógica de causa efecto en el fenómeno control.
6. Al finalizar la interacción, se sugiere elaborar algunas conclusiones sobre las ventajas de los modelos, por ejemplo, su capacidad para controlar variables teóricamente, que en la práctica pueden ser difíciles de manejar.
Créditos
Autor
Oscar Escamilla González
Propuesta de contenido
María Alejandra González Dávila
Adaptación a DescartesJS: Juan Gmo. Rivera Berrío y José R. Galo Sánchez (2016)
Esta unidad interactiva fue desarrollada en el ILCE por el equipo de Ciencias II.
Sus contenidos se distribuyen bajo una licencia de

La unidad utiliza Descartes que es software libre.
