Base binaria, decimal y hexadecimal
Ya se mencionó que el sistema binario se usa cuando se tienen fenómenos que sólo adoptan dos opciones y no hay un estado intermedio. Por ejemplo, un circuito eléctrico puede estar cerrado o abierto. Tampoco hay un estado intermedio (no hay una opción de medio abierto).
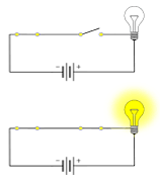
Para el ejemplo de los circuitos, podemos asignarle un símbolo a los circuitos abiertos (donde no pasa corriente) y uno a los cerrados (donde sí pasa corriente). Podríamos usar como símbolos un tache y una paloma, como se muestra a continuación.
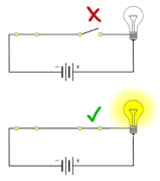
Pero usemos mejor un par de números: el cero (0) y el uno (1) respectivamente. Al haber sólo dos estados posibles, éstos son los únicos dos símbolos de los que podemos echar mano (no existen el 2, 3, 4, y demás símbolos numéricos que conoces). Si un circuito está abierto usamos el símbolo 0 y si está cerrado el 1, como se muestra a continuación.
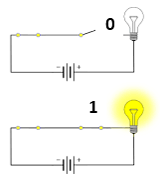
¿Cómo es entonces que una computadora, que está formada por circuitos, pueda representar símbolos más allá del 0 y el 1? La respuesta a eso es que no cuenta con un único circuito. Cuenta con varios, y esto le permite contar más allá de dos símbolos. A este sistema de conteo donde sólo tenemos dos símbolos (el cero y el uno) en lugar de diez (del 0 al 9) como en el sistema decimal común y corriente, se le conoce como sistema binario. Nosotros pensamos de forma natural en sistema decimal, pero para la construcción de una computadora es necesario saber cómo pasar de decimal a binario, y de binario a decimal. Es esto precisamente lo que se llama un cambio de base.
Ahora ya sabes que existe, además del sistema decimal que ya conoces, uno de base más pequeña que el decimal y que se llama binario. ¿Habrá otras bases además de éstas? En particular, ¿habrá bases que usen más símbolos que la conocida decimal? La respuesta es sí. Existe una base conocida como hexadecimal que tiene 16 diferentes símbolos. Aquí la cosa se pone interesante. Estamos acostumbrados a la base decimal y sus diez únicos símbolos, así que tendremos que echar mano de más símbolos de alguna manera. Pero verás que también es posible contar cosas con esta base y que se pueden traducir valores de la base decimal a la hexadecimal y viceversa.
Créditos
| Diseño del contenido | Alejandro Radillo Díaz, LITE |
| Diseño funcional | Alejandro Radillo Díaz, LITE |
| Programación | Alejandro Radillo Díaz, LITE |
| Asesoría de programación | Oscar Escamilla González, LITE |
| Diseño gráfico | Francisco Varela Fuentes |
| Coordinación | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

