Processing math: 100%

Algoritmo de Euclides y algoritmos computacionales

En la actualidad existen muchos algoritmos computacionales que simulan el algoritmo de Euclides. A continuación te presentamos algunos de ellos:

***

En Java:

***Primero se declara una función llamada "Euclides", la cual se evaluará en las variables enteras "n1" y "n2".

intEuclides(intn1,intn2) {

***A continuación se genera un ciclo en el cuál se obtiene el residuo de la división entre n1 y n2 mediante "%", el proceso se repite hasta que el residuo sea cero, y por el algoritmo explicado al inicio, sabemos que el penúltimo residuo es el MCD.

intr=n1

while(r!=0) {

n1=n2;

n2=r;

r=n1

 }

returnn2;

 }

***

En C:

***En las siguientes dos líneas lo que hace el código es llamar a 2 tipos de librerías que necesita el programa para poder hacer operaciones algebraicas, las librerías son "stdio.h" y "stdlib.h".

#include<stdio.h>

#include<stdlib.h>

***"int main()" Es la función principal del programa, dentro de ésta se deben declarar las variables y funciones globales que se utilizarán en todo el programa.

intmain()

 {

***Aquí se coloca la palabra “int” la cual está declarando la existencia de tres números enteros, "printf" permite que el usuario pueda introducir un valor, el cual se le asignara a "n1" con ayuda de "scanf". El mismo proceso se hace para "n2"

intr=0,n1,n2;

printf("introduzcan1:");

scanf("%d",&n1);

printf("introduzcan2:");

scanf("%d",&n2);

***A continuación se genera un ciclo de tipo "if", lo que se hace es sacar el residuo del cociente de los dos números que se introdujeron, mediante "%", proceso se repite varias veces hasta que el residuo sea cero, como se explicó al inicio de la unidad.

if(r==0)

 {

while(n2>0)

 {

r=n2%n1;

n1=n2;

n2=r;

 };

***Finalmente "print" muestra en la pantalla el valor del MCD y para finalizar el programa la función principal se regresa a cero mediante "return 0".

printf("elMCD:%d",&n1);

return0;

 }

 }

***

En C++:

***En las siguientes dos líneas lo que hace el código es llamar a 2 tipos de librerías que necesita el programa para poder hacer operaciones algebraicas, las librerías son "stdio.h" y "stdlib.h".

#include<stdio.h>

#include<stdlib.h>

usingnamespacestd;

***"int mcd(int x, int y)" Es una función, en la cual se está declarando que se va a trabajar con dos valores enteros, "x" y "y".

intmcd(intx,inty) {

>***Dentro de la función se declara otra variable , "t", y después se analiza como son los valores de "x" y "y", si estos son negativos, se cambian a positivos, a la variable t se le asigna el valor más pequeño entre "x" y "y".

intt;

x=(x<0)?−x:x;

y=(y<0)?−y:y;

t=(x<y)?x:y;

***A continuación se genera un ciclo de tipo "while", lo que se hace es sacar el residuo del cociente de "x" entre "t" y "y" entre "t", el ciclo se detiene cuando alguno de los dos residuos es cero, lo cual significa que ya se encontró el MCD.

while((x%t)||(y%t))

−−t;

returnt;

 }

inteuc(intx,inty) {

return(!y)?x:euc(y,x%y);

 }

***A continuación se solicita al usuario que introduzca el valor de "x" y "y" mediante "cout" y "cin". Finalmente se imprime el valor del MCD, el cual se obtiene al llamar la función “mcd()”, evaluada en los valores "x" y "y" que se acaban de introducir.

intmain()

 {

intx,y;

cout<<"x:";

cin>>x;

cout<<"y:";

cin>>y;

cout<<"MCD:"<<mcd(x,y)<<endl;

cout<<"MCD(euclides):"<<euc(x,y)<<endl;

 }

***

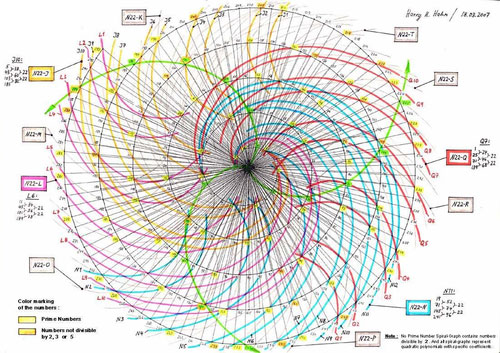
La imagen muestra la representación de la secuencia de un algoritmo, tal algoritmo es la espiral de Teodoro cuya geometría tiene varias propiedades incluyendo una que se relaciona con el MCD.

©