Ecuación diferencial de Bernoulli
Una E.D. (Ecuación diferencial) de la forma dydx+p(x)y=Q(x)yn con n≠0 y n≠1, se le llama E.D. de Bernoulli y es una E.D. no lineal de primer orden. Si n=0 la ecuación quedaría como dydx+p(x)y=Q(x), que es una ecuación lineal no homogénea y sería fácil resolverla, pues si n=1 la ecuación quedaría como dydx+(p(x)−Q(x))y=0 ⇒ dydx+R(x)y=0 que es una E.D. lineal homogénea, que es mucho más fácil de resolver que la ecuación anterior.
La ecuación de Bernoulli se puede convertir en una E.D. lineal de primer orden mediante la sustitución w=y1−n:
Esto implica que nos podemos centrar simplemente en resolver E.D. lineales de primer orden. A continuación veremos un ejemplo de una ecuación de Bernoulli.
Ejemplo:
Sea la ecuación xy(1+xy2)dydx=1 con y(1)=0.
Solución:
Despejamos dydx y obtenemos dydx=1xy(1+xy2), invertimos la ecuación
Ésta última tiene la forma de la ecuación de Bernoulli con variable dependiente x, y con n=2. Hagamos w=x1−n=x1−2=x−1 ⇒ x=w−1, derivamos ésta última con respecto as y y obtenemos dxdy=−w−2dwdy. Sustituimos en (1) para obtener −w−2dwdy−yw−1=y3w−2, multiplicamos por −w2 y finalmente nos queda dwdy+yw=−y3, una E.D. lineal de primer orden donde p(y)=y;Q(y)=−y3
La función solución a la ecuación diferencial se puede obtener mediante el método del factor integrante. La función es:
Como hicimos un cambio de variable, tenemos que regresar a las variables originales utilizando el mismo cambio de variables:
Como ya hemos visto, esta solución obtenida es la solución general, y a partir de ésta, junto con las condiciones iniciales, podemos obtener la ecuación particular. Como y(1)=0 podemos evaluar estos valores, despejamos a c y obtenemos que c=−1, por lo tanto la solución particular es:
En el siguiente espacio se muestra la gráfica de la solución particular. Utiliza los pulsadores para cambiar el valor de c y nota cómo es el comportamiento de dicha gráfica para diferentes valores.
Como pudimos notar, es importante centrarnos en el estudio de métodos que nos ayudan a resolver ecuaciones diferenciales lineales de primer orden. En algunos caso estos métodos son demasiado engorrosos, por lo que a continuación veremos la interpretación geométrica como una técnica de solucion en donde el punto de vista geométrico es particularmente útil.
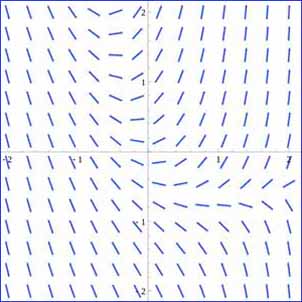
La siguiente imagen representa el campo vectorial de una ecuación diferencial, y en él se puede ver cómo son sus soluciones. En los siguientes apartados analizaremos cómo podemos generar este tipo de campos y de qué forma nos dan información de un fenómeno.
Créditos
Escena original
| Diseño del contenido | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Diseño funcional | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Programación | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Diseño gráfico | Ricardo López Gómez |
| Coordinación | Leticia Montserrat Vargas Rocha |
Adaptación
| Diseño funcional | Victor Hugo García Jarillo (Facultad de Ciencias, UNAM) |
| Programación | Victor Hugo García Jarillo (Facultad de Ciencias, UNAM) |
| Diseño gráfico | Francisco Varela Fuentes |
| Coordinación | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

