Estudio de poblaciones y ecuaciones diferenciales
Modelos de crecimiento
En general, en un sistema poblacional, el número de individuos en un instante futuro es el resultado de sumar los individuos que nacerán hasta el instante futuro a la población actual, y los individuos que se incorporarán por inmigración, además hay que restar los individuos que perecerán por diversas características y los individuos que emigrarán.
Para describir el sistema debemos hacer algunas consideraciones que nos llevan a un problema simplificado, y en el caso más sencillo, podremos modelar tal situación mediante una ecuación diferencial lineal de primer orden con sus respectivas condiciones iniciales:
Afortunadamente para el caso de las ecuaciones diferenciales lineales de primer orden existen diversos métodos para poder resolverlas. Usando el método de separación de variables llegamos a que la solución de la ecuación anterior está dada por la función y(t)=y0ekt
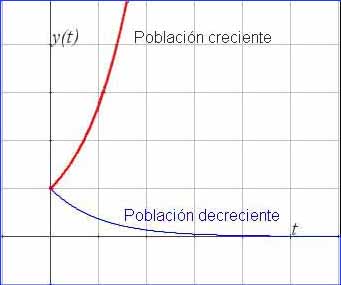
La forma de la solución nos permite ver que el número de individuos crece de forma exponencial si el valor de k es positivo o decrece de forma exponencial si el valor de k es negativo.
En general, no es razonable suponer un crecimiento de la población como el descrito anteriormente. Es más realista introducir algún factor externo que suponga un freno en el crecimiento, por ejemplo, la existencia de depredadores que reduzcan el número de individuos de una población, la limitación de los recursos alimenticios, el confinamiento espacial de la población, etc. Como consecuencia de agregar estos factores la representación matemática correspondiente nos conduce a ecuaciones diferenciales no lineales del estilo de la ecuación de Bernoulli, de tal forma que podemos llevarlas a la forma de un sistema lineal que, como ya vimos, es más fácil resolver.
Un ejemplo de modelado por medio de una ecuación de Bernoulli es el caso de la propagación de enfermedades, en donde la velocidad de propagación de una enfermedad es proporcional a la probabilidad de que un individuo infecte a otro, multiplicado por el número de individuos infectados N.
La probabilidad (P) de que un individuo infecte a otro es proporcional a la relación entre individuos sanos N0−N y la cantidad total N0 de individuos, P=(N0−NN0).dNdt=N(N0−NN0)
dNdt=N−N2N0
dNdt−N=(−1N0)N2
La última ecuación es no lineal y tiene la forma de la ecuación de Bernoulli:
dydt+p(x)y=Q(x)yn
A continuación analizaremos cómo nos ayuda este tipo de ecuaciones.
©Créditos
Escena original
| Diseño del contenido | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Diseño funcional | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Programación | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Diseño gráfico | Ricardo López Gómez |
| Coordinación | Leticia Montserrat Vargas Rocha |
Adaptación
| Diseño funcional | Victor Hugo García Jarillo (Facultad de Ciencias, UNAM) |
| Programación | Victor Hugo García Jarillo (Facultad de Ciencias, UNAM) |
| Diseño gráfico | Francisco Varela Fuentes |
| Coordinación | Leticia Montserrat Vargas Rocha |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

