Como recordarás, una transformación lineal entre dos espacios vectoriales \(E\) y \(F\) es una correspondencia \(A:E \longrightarrow F\) que a cada vector \(v\in E\) le asigna un vector \(A(v)=Av \in F\) tal que, para cualesquiera \(u, v \in E\) y \(\alpha \in \mathbb{R}\) se cumplan las relaciones:

  \[ \begin{eqnarray} \nonumber A(u+v) & = & Au+ Av,\\ \nonumber A(\alpha v) & = & \alpha \cdot Av \\ \end{eqnarray} \]    

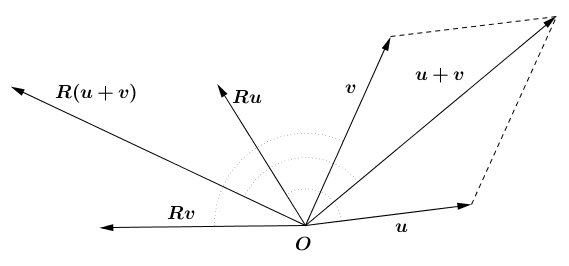
Rotaciones

 

La rotación de un ángulo \(\theta\) en torno del origen de \(\mathbb{R}^2\), es un operador \(R:\mathbb{R}^2 \longrightarrow \mathbb{R}^2\), que lleva cada vector \(v\) en el vector \(Rv\) que resulta de \(v\) por la rotación de un ángulo \(\theta\) en torno del origen. En la siguiente figura, es evidente cómo \(R(u+v) = R\cdot u+ R\cdot v\) y \(R(\alpha v)=\alpha R \cdot v\) para \(v \in \mathbb{R}^2\) y \(\alpha \in \mathbb{R}\): Luego \(R\) es una transformación lineal, ¡pero ésto ya lo sabías!.

 

Finalmente, para determinar la matríz de rotación para un vector arbitrario \(v=\left( x,y\right) \in \mathbb{R}^2\), sea \(R\cdot v = \left( x^{\prime },y^{\prime }\right)\). Sabemos que

\[ \begin{eqnarray*} \nonumber x^{\prime } & = & ax+by, \\ \nonumber y^{\prime } & = & cx+dy, \\ \end{eqnarray*} \]

y queremos determinar la matriz

\[ \begin{equation} \left( \begin{array}{cc} a & b \\ c & d% \end{array}% \right) \end{equation} \]  

dónde \(Re_{1}=(a,c)\) y \(Re_{2}=(b,d)\), con \(e_{1}=(1,0)\) y \(e_{2}=(0,1)\).

 

Recordemos que, por las definiciones de seno y coseno, el vector \(Re_{1}\) (que forma con \(e_{1}\) un ángulo \(\theta\), tiene coordenadas \(Re_{1}= (\cos \theta, \sin \theta)\), y cómo \(e_{1}\perp e_{2}\) tendremos que \(Re_{1}\perp Re_{2}\), luego \(Re_{2}= (-\sin \theta, \cos \theta)\).

 

De modo que la rotación \(R:\mathbb{R}^2 \longrightarrow \mathbb{R}^2\) lleva un vector \(v=(x,y)\) en el vector \(Rv=(x^{\prime },y^{\prime })\), donde

\[ \begin{eqnarray*} \nonumber x^{\prime} & = & x\cos \theta - y\sin \theta, \\ \nonumber y^{\prime} & = & x\sin \theta + y\cos \theta. \\ \end{eqnarray*} \]  

Y por lo tanto, la matriz \(R\), relativa la base canónica de \(\mathbb{R}^2\) es

  \[ \begin{equation} \left( \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta% \end{array}% \right) \end{equation} \]    

Proyección ortogonal sobre una recta

Como recordarás, la recta \(y=ax\) es el conjunto de puntos \((x,ax) \in \mathbb{R}^2\) donde \(x\) varía en \(\mathbb{R}\). A su vez, es el subespacio vectorial de \(\mathbb{R}^2\) generado por el vector \((1,\alpha)\). Sea \(P: \mathbb{R}^2 \longrightarrow \mathbb{R}^2\) el operador que a cada \(v=(x,y) \in \mathbb{R}^2\) le hace corresponder el vector \(Pv=(x^{\prime}, a x^{\prime})\) que tiene por extremo el pie de la perpendicular que parte de \(v\) hacia la recta \(y=ax\).

   

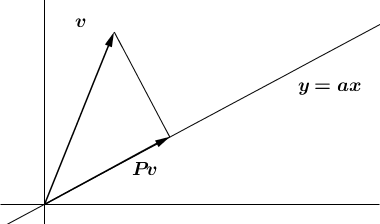
Nos gustaría poder calcular \(x^{\prime}\) en función de \(x\) e \(y\), con lo que obtendríamos las coordenadas \((x^{\prime},ax^{\prime})\) de \(Pv\) en función de las coordenadas de \(v\). Cuándo \(a=0\), la recta \(y=ax\) es el eje de las abcisas y la proyección \(Pv\) será, justamente, igual a \((x,0)\). Por lo tanto, las ecuaciones de la proyección \(P\) sobre el eje horizontal son \(x^{\prime}=x\), \(y^{\prime}=0\). Así, la matriz de \(P\) en la base canónica de \(\mathbb{R}^2\) es \(\bigl(\begin{smallmatrix} 1&0\\ 0&0 \end{smallmatrix} \bigr)\). Y como caso general, el extremo del vector \(Pv\) será el vértice del ángulo recto en un triángulo rectángulo cuyos otros vértices son el origen y el extremo del vector \(v\).

 

Aplicando el Teorema de Pitágoras, veremos que:

  \[ \begin{equation} (\textsf{dist}(v,0))^2 = (\textsf{dist}(Pv,0))^2 + (\textsf{dist}(v,Pv))^2 \end{equation} \]  

luego

  \[ \begin{equation} x^2 + y^2 = (x^{\prime})^2 + (x - x^{\prime})^2 + (y - ax^{\prime})^2. \end{equation} \]  

Supongamos \(x^{\prime} \neq 0\). Desarrollando, simplificando y dividiendo ambos términos de la igualdad entre \(x^{\prime}\) obtenemos \((1+a^2)x^{\prime}=x+ay\), a partir de dónde \(x^{\prime}=\frac{x+ay}{1+a^2}\), luego \(x^{\prime}=\frac{1}{1+a^2}x+\frac{a}{a+a^2}y\).

 

El caso \(x^{\prime}\) nos dice que \(v=(x,y)\) está sobre la recta perpendicular a la recta \(y=ax\) pasando por el origen. Pero la ecuación de dicha perpendicular es \(x + ay = 0\), luego la la expresión \(x^{\prime} = (x+ay) \diagup (1+a^2)\) establece en todos los casos a \(x^{\prime}\) en función de \(x\) e \(y\). Notemos que en particular, la proyección \(P: \mathbb{R}^2 \longrightarrow \mathbb{R}^2\) es un operador lineal, y su matriz en la base canónica de \(\mathbb{R}^2\) es

  \[ \begin{equation} \left( \begin{array}{cc} \frac{1}{1+a^2} & \frac{a}{1+a^2} \\ \frac{a}{1+a^2} & \frac{a^2}{1+a^2}% \end{array}% \right) \end{equation} \]    

Reflexiones

 

Tomemos \(S: \mathbb{R}^2 \longrightarrow \mathbb{R}^2\) la reflexión respecto a la recta \(y=ax\). Y observemos que, para todo \(v=(x,y) \in \mathbb{R}^2\) la recta \(y=ax\) es la bisectriz del ángulo entre \(v\) y \(Sv\), además es perpendicular a la recta que pasa por \(v\) y \(Sv\). Sea \(P: \mathbb{R}^2 \longrightarrow \mathbb{R}^2\) la proyección ortogonal sobre la recta \(y=ax\). La siguiente figura, muestra que, para todo \(v \in \mathbb{R}^2\), se tiene \(v+Sv=2Pv\), es decir, que \(I+S=2P\), donde \(I: \mathbb{R}^2 \longrightarrow \mathbb{R}^2\) es el operador indentidad.

   

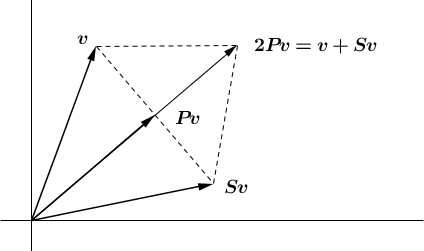
De aquí se deduce, que \(S=2P-I\), y por lo que vimos en el caso de las proyecciones, concluimos que, para todo \(v=(x,y)\), se cumple que \(Sv=(x^{\prime},y^{\prime})\). Donde \((x^{\prime},y^{\prime})\) resulta de aplicarle a \((x,y)\) la siguiente matriz

  \[ \begin{equation} \left( \begin{array}{cc} \frac{1-a^2}{1+a^2} & \frac{2a}{1+a^2} \\ \frac{2a}{1+a^2} & \frac{a^2 - 1}{1+a^2}% \end{array}% \right). \end{equation} \]

Homotecias

 

El caso de las homotecias es mucho más simple, pues se trata de un cambio en la escala, es decir si \(H: \mathbb{R}^2 \longrightarrow \mathbb{R}^2\) es el operador que a cada vector \(v \in \mathbb{R}^2 \) le asocia el vector \(Hv=k\cdot v\), con \(k \in \mathbb{R}\) la constante de homotecia, evidentemente el operador \(H\) será una transformación lineal; luego, bajo el cambio de escala obtendremos que si \(e_{1}=(1,0)\), \(e_{2}=(0,1)\) entonces \(He_{1}=(k,0)\) y \(He_{2}=(0,k)\). De donde se deduce que la matriz asociada a esta transformación lineal es:

  \[ \begin{equation} \left( \begin{array}{cc} k & 0 \\ 0 & k% \end{array}% \right) \end{equation} \]