Definición de rotacional
Definiremos de forma algebraica el rotacional de un campo vectorial. Éste asocia a un campo vectorial en R3, ˉF=F1ˉi+F2ˉj+F3ˉk=(F1,F2,F3), otro campo vectorial rot ˉF, definido como:
Para saber cómo se obtiene esta larga ecuación, podemos utilzar la notación de "operadores", los cuales actúan u operan a funciones con valores reales, un operador muy conocido, es el operador ∇, definido como:
Entonces, si este operador actúa en una función f, se obtiene:
Esto se conoce como el gradiente de f. Ahora si consideramos ∇ como un vector de componentes ∂/∂x,∂/∂y,∂/∂z, entonces podemos tomar el producto cruz ∇×ˉF:
Así, el rotacional rot ˉF es igual que ∇×ˉF, y a menudo se usa esta última expresión.
Explicar el significado físico del rotacional es bastante complicado, sin embargo a continuación consideraremos una situación simple que muestra cómo el rotacional está asociado a giros.
Como el rotacional se aplica a campos vectoriales veamos un ejemplo de estos, la fuerza de atracción gravitatoria entre dos objetos de masas M y m:
Podemos escribir el campo de fuerza gravitatoria en términos de sus funciones componentes como:
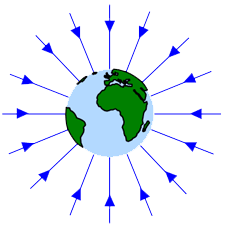
Este campo se representa gráficamente mediante flechas en dirección radial apuntando hacia el origen de coordenadas, de longitud cada vez menor a medida que el objeto m se aleja del objeto M.
Créditos
Escena original
| Diseño del contenido | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Diseño funcional | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Programación | Víctor Hugo García Jarillo (Facultad de Ciencias UNAM, LITE) |
| Diseño gráfico | Ricardo López Gómez |
| Coordinación | Leticia Montserrat Vargas Rocha |
Adaptación
| Diseño funcional | Victor Hugo García Jarillo (Facultad de Ciencias, UNAM) |
| Programación | Victor Hugo García Jarillo (Facultad de Ciencias, UNAM) |
| Diseño gráfico | Francisco Varela Fuentes |
| Coordinación | Leticia Montserrat Vargas Rocha |
| Desarrollo del contenedor | Oscar Escamilla González |
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons Reconocimiento-NoComercial-CompartirIgual.
La unidad didáctica fue creada con Arquímedes, una herramienta de código abierto.
La unidad didáctica contiene escenas elaboradas con Descartes, una herramienta de código abierto.
LITE - UnADM 2014

