Diagramas de Argand

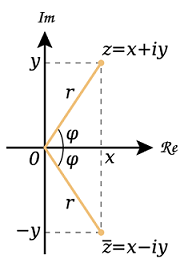
Hay dos representaciones geométricas del número complejo $z=x+iy$

1. como el punto $P(x,y)$
2. como el vector $\overrightarrow{OP}$ del origen a $P$

En cada representación, el $eje-x$ es el eje real y el $eje-y$ es el eje imaginario. Ambas representaciones son diagramas de Argand de $x+iy$. En términos de las coordenadas polares de $x$ y $y$, se tiene que

$x=r \cos \varphi \ \ \ \ \ y=r \sin \varphi$

y $$z=x+iy=r(\cos \varphi +i \sin \varphi )$$

Definimos el valor absoluto o módulo de un número complejo $x+iy$ (o su magnitud), como la longitud $r$ del vector $\overrightarrow{OP}$, así $$|x+iy|=\sqrt{x^2+y^2}$$ Si siempre elegimos las coordenadas polares $r$ y $\varphi$ de manera que $r$ no sea negativo, entonces $$r=|x+iy|$$

El ángulo $\varphi$ se llama argumento de $z$ y se escribe como $\varphi=arg$ $z$. Por supuesto, cualquier entero múltiplo de $2 \pi$ pude sumársele a $\varphi$ para obtener otro ángulo apropiado.

La siguiente ecuación nos da una fórmula muy útil que relaciona un número complejo $z$, su conjugado $\overline{z}$ y su módulo $|z|$ $$z\cdot \overline{z} =|z|^2$$

Producto de números complejos

Si expresamos dos números complejos en términos de sus coordenadas polares, digamos $z_1=r_1(\cos \varphi_1 +i \sin \varphi_1 )$ y $z_2=r_2(\cos \varphi_2 +i \sin \varphi_2 )$, entonces el producto de esto dos número complejos se puede expresar como $$z_1z_2=r_1r_2(\cos \varphi_1 +i \sin \varphi_1 )(\cos \varphi_2 +i \sin \varphi_2 )$$ Multiplicando término a término, y usando identidades trigonométricas, se llega a que $$z_1z_2=r_1r_2(\cos (\varphi_1+\varphi_2)+i \sin (\varphi_1+\varphi_2))$$ que es la expresión de un número complejo con módulo $r_1r_2$ y argumento $\varphi_1+\varphi_2$

Potencias de números complejos

El resultado anterior puede extenderse para el producto de $n$ números complejos. Si los $n$ números complejos en cuestión son el mismo número, tenemos el número elevado a la $n$, es decir $z^n=(r\cos \varphi + i r\sin \varphi)^n$, pero $$(\cos \varphi + i \sin \varphi)^n=\cos n\varphi + i \sin n\varphi$$ por lo que $$z^n=r^n(\cos n\varphi + i \sin n\varphi )$$
La segunda igualdad es el enunciado del Teorema de De Moivre.

De lo anterior se deriva que si $z=r(\cos \varphi + i \sin \varphi)$ es un número complejo distinto de cero, y $n$ es un entero positivo, entonces hay $n$ números complejos diferentes entre sí que son raíces $n-ésimas$ de $z$. Para ver por qué, tomemos $w=\rho (\cos \alpha + i \sin \alpha )$, una raíz $n-ésima$ de $z$, entonces $w^n=z$, o $$\rho^n (\cos n\alpha + i \sin n\alpha )=r(\cos \varphi + i \sin \varphi )$$ entonces $\rho=\sqrt[n]{r}$ es la raíz $n-ésima$ real positiva de $r$. En cuanto al ángulo, aunque no podemos decir que $n\alpha$ y $\varphi$ son iguales, podemos decir que difieren solamente por un entero múltimplo de $2\pi$. Es decir, $$n\alpha=\varphi+2k\pi$$ con $k=0,\pm 1, \pm2,...$. Entonces $$\alpha=\frac{\varphi}{n}+k\frac{2\pi}{n}$$ Por lo que las $n$ raíces de $z$ están dadas por $$\sqrt[n]{r(\cos \varphi + i \sin \varphi )}=\sqrt[n]{r}\Bigl(\cos \Bigl(\frac{\varphi}{n}+k\frac{2\pi}{n}\Bigr)+ i \sin \Bigl(\frac{\varphi}{n}+k\frac{2\pi}{n}\Bigr)\Bigr)$$

En la siguiente escena hablaremos acerca de las raíces de un polinomio de grado $n$.