Objetivo

Obtener, a partir de su gráfica, el punto de discontinuidad de una función.

Conceptos básicos

Nota. Esta lección está escrita de manera que el concepto de continuidad no dependa del concepto de límite. Ya que es mucho más natural el concepto de continuidad que el de límite. Más aún, nuestra sugerencia es que primero se vea el tema de continuidad y luego el de límite.

Si una función está definida en un punto $p$, decimos que es continua en ese punto si $f(x)$ es casi igual a $f(p)$ para toda $x$ que sea casi igual a $p$. En símbolos escribimos:

Si $x ≈ p$, entonces $f(x) ≈ f(p)$

donde el símbolo $≈$ sirve para indicar que dos números son muy parecidos (casi iguales).

Nota del revisor:

Intuitivamente entenderemos que una función $y=f(x)$ es continua en un intervalo del dominio si podemos dibujar su gráfica de un solo trazo. Si en algún punto "se rompe" diremos que presenta una discontinuidad en dicho punto. Algunos ejemplos o tipos de discontinuidades se muestran en la siguiente imagen:

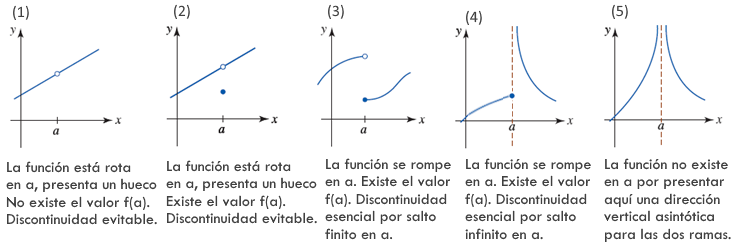
La discontinuidad se dice que es $evitable$ cuando basta asignar al hueco existente el valor que debe tener la función en $a$ para hacerla continua. Son los casos $1$ y $2$ de la imagen. Cuando la discontinuidad no es $evitable$ en $a$, se dice que hay una discontinuidad $esencial$ en $a$, casos $3$, $4$ y $5$.

La gran mayoría de las funciones que utilizamos cotidianamente son continuas en todos los números donde están definidas.

• Las funciones polinomiales $f(x)=c_{n}x^{n}+c_{n-1}x^{n-1}+...+c_{1}x+c_{0}$ son continuas en todos los reales.

• Las funciones racionales, es decir, los cocientes de funciones polinomiales

  $$h(x)=\frac{f(x)}{g(x)}$$

  son continuas en todos los números $p$ para los cuales $g(p)≠0$.

• Las funciones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante son continuas en todos los números donde están definidas.
• Las funciones logaritmo y exponencial son continuas en todos los números donde están definidas.

En la gráfica puedes hacer zoom con el pulsador de la esquina inferior derecha y también puedes arrastrar el plano para desplazarlo.

Procedimiento

Vamos ahora a identificar geométricamente los números donde una función es discontinua, es decir, donde no es continua.

• Si una función no está definida en un numero, ni siquiera tiene sentido preguntarse si es continua.
• Una función $f$ definida en un número $p$ es discontinua en $p$ si hay números $x$ muy cercanos a $p$ para los cuales el valor de la función ahí, $f(x)$ está lejos de $f(p)$.

Ejemplos

Ejercicios

Para resolver los siguientes ejercicios, posiblemente necesites hacer zoom con las flechas de la esquina de la imagen o arrastrar el plano para desplazarlo.