La elipse a partir de algunos de sus elementos
Ecuación ordinaria de la elipse no centrada en el origen dados el centro, un vértice y un foco

Objetivo

Obtener la ecuación ordinaria de una elipse con centro en $(h,k)$, conociendo un vértice y un foco.

Si la elipse, paralela a los ejes coordenados rectangulares $(X, Y)$, está centrada en el punto (h, k) podemos obtener fácilmente su ecuación ordinaria haciendo una traslación de ejes para que el centro de la elipse coincida con el nuevo origen del sistema $(X', Y')$.

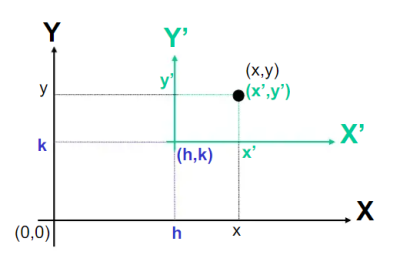
En el nuevo sistema, las coordenadas de un punto cualquiera $(x', y')$ se pueden expresar así $$x'=x-h$$ $$y'=y-k$$ En consecuencia la ecuación ordinaria de una elipse horizontal, referida al sistema (X', Y') cuyos ejes mayor y menor respectivamente son $a$ y $b$ se podrá escribir, como ya sabemos, así $$\frac{x'^2}{a^2} + \frac{y'^2}{b^2} = 1$$ y referida al sistema original $(X, Y)$ $$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$$

Procedimiento

Con los datos obtenemos la posición y orientación de la elipse, las literales $a$ y $c$, y por último, la literal $b$ para sustituir directamente en la ecuación ordinaria.

Solución

  1. Ubicamos el centro, el vértice y el foco en una gráfica para determinar la posición y orientación de la elipse. Criterios:
    • Si los tres están sobre una misma línea horizontal, ésa es la orientación de la elipse.
    • Si los tres están sobre una misma línea vertical, ésa es la orientación de la elipse.
  2. La distancia desde el centro hasta el vértice corresponde a la literal $a$.
  3. La distancia desde el centro hasta el foco corresponde a la literal $c$.
  4. Determinamos el valor de la literal $b$ con la siguiente relación, que es el teorema de Pitágoras:
    5. $$a^{2}=b^{2}+c^{2}$$
  5. Sustituimos las coordenadas del centro $(h,k)$ y las literales $a$ y $b$ en la ecuación ordinaria que corresponda a la orientación de la elipse.

Ejemplos

A continuación se describe el procedimiento para obtener la ecuación ordinaria de una elipse con centro en $(h,k),$conociendo un vértice y un foco. Presiona Continuar.

Ejercicios

Obtener la ecuación ordinaria de una elipse con centro en $(h,k)$, a partir de los datos dados.

Esta unidad ha sido revisada, adaptada y corregida en enero de 2022 para ser publicada en la Web de RED Descartes dentro del subproyecto denominado Prometeo, modificando el nombre que le dieron en la versión original para adaptarlo a su contenido, cuyos créditos se reflejan después de este apartado.

Actualización: Ángel Cabezudo Bueno

Unidades interactivas para bachillerato desarrolladas por la Dirección General de Evaluación Educativa de la UNAM en colaboración con el Instituto de Matemáticas y el Proyecto Arquímedes.

Autor: Octavio Fonseca Ramos

Edición académica: Carlos Hernández Garciadiego y Octavio Fonseca Ramos

Edición técnica: Norma Patricia Apodaca Alvarez y Fernando René Martínez Ortiz

Adaptado a DescartesJS en el proyecto LITE 2013 financiado por CONACyT.

Adaptación: Víctor Hugo García Jarillo y Deyanira Monroy Zariñán

Asesoría técnica: José Luis Abreu León, Oscar Escamilla González y Joel Espinosa Longi

Adaptado para dispositivos móviles por la DGTIC en colaboración con el IMATE y el LITE. Diciembre de 2014.

Adaptación: Octavio Fonseca Ramos

Asesoría técnica: José Luis Abreu León y Joel Espinosa Longi

Coordinación: Deyanira Monroy Zariñán

Actualización tecnológica y de estilo, 2019.

Actualización: Joel Espinosa Longi

Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons, si no se indica lo contrario.

Los componentes interactivos fueron creados con Descartes que es un producto de código abierto.