Objetivo
Obtener la ecuación ordinaria de una parábola con vértice en el origen y foco conocido.
Ecuación ordinaria
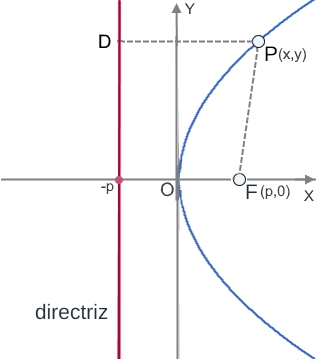
Para hallar la ecuación de la parábola se toma un sistema de referencia donde el eje OX coincida con el eje polar y el origen $O(0,0)$ coincida con el vértice.
El parámetro $p$ llamado distancia focal, es la distancia del foco al vértice. La directriz corta al eje polar en el punto $(-p,0)$. Cualquier punto $P(x,y)$ de la parábola equidista del foco $F(p,0)$ y de la directriz $x=-p$. En consecuencia el vértice (como punto de la parábola) equidista del foco y de la directriz. La distancia entre el foco y la directriz es $2p$, la que se conoce como parámetro de la parábola.
Dado que $PF=PD$, igualando estas distancias respectivas tenemos $$\sqrt{(x-p)^2+(y-0)^2}=x+p$$ elevando al cuadrado $$x^2-2px+p^2+y^2=x^2+2px+p^2$$ y simplificando, se obtiene la ecuación ordinaria de la parábola $$y^2=4px$$ Observar que la parabola considerada tiene por eje polar el eje OX, por lo que se denomina parábola horizontal y ésta envuelve al foco que queda a la derecha del vértice (abre hacia la derecha). Otros casos de parábola son posibles y su ecuación ordinaria también cambia, son los que se indican el el apartado siguiente y son fáciles de entender.
Recordatorio
La ecuación ordinaria de una parábola horizontal con vértice en el origen es de la forma:
$y^{2}=4px$, si abre hacia la derecha $y^{2}=-4px$, si abre hacia la izquierda $(1)$
en donde $p$ es la distancia del vértice al foco.
La ecuación ordinaria de una parábola vertical con vértice en el origen es de la forma:
$x^{2}=4py$, si abre hacia arriba $x^{2}=-4py$, si abre hacia abajo $(2)$
en donde $p$ es la distancia del vértice al foco.
Procedimiento
Para determinar la forma ordinaria de la parábola con vértice en el origen y foco conocido:
- Se calcula $p$, la distancia del vértice, que en este caso es el origen $(0,0)$, al foco.
- La ecuación se elige considerando lo mostrado en (1) o (2), es decir, si el foco está en el eje $X$ o en el $Y$.
- Se elige el signo tomando en cuenta la posición del vértice respecto al foco.
Solución
En el cuadro interactivo (escena), el foco es un control gráfico que puede cambiar de posición. Se puede arrastrar a lo largo del eje y observar cómo se modifica tanto la gráfica, como la ecuación ordinaria de la parábola cuando la abcisa del foco en la parábola horizontal o la ordenada del foco en la parábola vertical asumen valores tanto negativos como positivos. Analiza cada caso y compara dichos resultados con los del recuadro anterior. El pulsador situado en el extremo inferior derecho de los gráficos te permitirá acercar o alejar la imagen.
Parábola horizontal Parábola vertical
Foco en $(h,0)$ Foco en $(0,k)$
Ejemplos
En el siguiente recuadro interactivo, observa cómo se encuentra la ecuación ordinaria de la parábola con centro en el origen y foco $(h,0)$ o $(0,k)$. Presiona el pulsador que se sitúa debajo del ejercicio y avanza en la solución, tratando de comprender cada uno de los pasos. Analiza otros ejemplos al dar clic en el botón que se localiza en el extremo inferior derecho del cuadro.
Ejercicios
Determina lo que se te pida en cada caso. Escribe el resultado en los campos de texto del cuadro y presiona ↲. Si tu respuesta es correcta, se inhabilitará el campo de texto; en caso contrario, deberás reintentarlo. Al terminar se desplegará el botón que te permitirá hacer otro ejercicio.
Esta unidad ha sido revisada, adaptada, ampliada y corregida en junio de 2021 para ser publicada en la Web de RED Descartes dentro del subproyecto denominado Prometeo, manteniendo el mismo nombre que le dieron en la versión original, cuyos créditos se reflejan después de este apartado.
Actualización: Ángel Cabezudo Bueno
Unidades interactivas para bachillerato desarrolladas por la Dirección General de Evaluación Educativa de la UNAM en colaboración con el Instituto de Matemáticas y el Proyecto Arquímedes.
Autores: Carlos Hernández Garciadiego y Eréndira Itzel García Islas
Edición académica: José Luis Abreu León, Carlos Hernández Garciadiego y Alejandro Radillo Díaz
Edición técnica: Norma Patricia Apodaca Alvarez y Fernando René Martínez Ortiz
Adaptado a DescartesJS en el proyecto LITE 2013 financiado por CONACyT.
Adaptación: Víctor Hugo García Jarillo y Deyanira Monroy Zariñán
Asesoría técnica: José Luis Abreu León, Oscar Escamilla González y Joel Espinosa Longi
Adaptado para dispositivos móviles por la DGTIC en colaboración con el IMATE y el LITE. Diciembre de 2014.
Adaptación: Juan José Rivaud Gallardo
Asesoría técnica: José Luis Abreu León y Joel Espinosa Longi
Coordinación: Deyanira Monroy Zariñán
Actualización tecnológica y de estilo, 2019.
Actualización: Joel Espinosa Longi
Los contenidos de esta unidad didáctica interactiva están bajo una licencia Creative Commons, si no se indica lo contrario.
Los componentes interactivos fueron creados con Descartes que es un producto de código abierto.