La función cuadrática y sus raíces

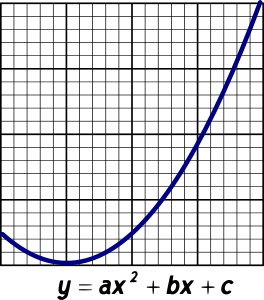
La función cuadrática, de la forma $y=ax^2+bx+c$, y cuya curva es una parábola, se manifiesta en muchos fenómenos naturales. Ejemplos cotidianos son el tiro parabólico y el movimiento uniformemente acelerado. También seguramente la has visto en aparatos tales como la antena parabólica, dado que sus propiedades geométricas permiten el enfoque de rayos que inciden paralelos sobre ella. Algunos potenciales en mecánica también pueden ser aproximados por una ecuación cuadrática. Así pues, como notas, la ecuación cuadrática es muy versátil y es útil que domines y entiendas sus conceptos básicos.

En esta unidad nos enfocaremos a las raíces de la función cuadrática (es decir, la coordenada $x$ de el o los puntos en los cuales la curva de la ecuación cruza el eje $X$ o, visto de otra manera, los valores en $x$ de la curva para los cuales $y=0$). En particular, analizaremos qué quiere decir que dichas raíces sean reales desde el punto de vista algebraico y gráfico.