Planteamiento del problema: El árbol genealógico de las abejas

Modelación algebraica de fenómenos

Para la descripción de fenómenos, muchas veces resulta útil el poder modelarlos de forma algebraica. Para ejemplificar esto, en la presente unidad abordamos un tema que es el conteo del número de abejas en una generación determinada de un árbol genealógico compuesto sólo por zánganos y reinas, y que sigue ciertas condiciones que son necesarias para establecer el conteo.

Aunque elegimos un ejemplo particular para trabajar de forma inicial, es importante que notes que cada ejemplo puede tener su modelo propio. Y para cada caso hay que analizar el comportamiento, sus reglas y, a partir de esto, pensar para poder generar el modelo.

Las reglas de reproducción de nuestro ejemplo de abejas

Como seguramente ya sabes, las abejas pueden ser hembras (reinas y obreras) y machos (zánganos). Las reinas y zánganos se encargan de la reproducción. La diferencia entre una obrera y una reina es que la obrera no contribuye a la reproducción; cuando una abeja hembra nace, se volverá reina u obrera sólo dependiendo del tipo de alimentación que recibe.

El modelo que analizaremos es una simplificación de la realidad en el sentido de que sólo consideraremos las abejas que contribuyen a la reproducción (reina y zángano), y descartaremos a las obreras. Así pues, aunque una reina podría tener obreras en su descendencia, no las estudiaremos. A pesar de eliminar a las obreras, los árboles genealógicos que formarán el objeto de nuestro análisis son una representación de la realidad para las abejas reinas y zánganos.

Es necesario tener claras las reglas que nos permiten saber cómo se construye el árbol genealógico de las abejas. Primero que nada, es importante aclarar que contaremos las generaciones hacia arriba, es decir, la generación cero es la última, la actual; la que se encuentra inmediatamente arriba de ésta (la generación 1) es la anterior, de la cual provino la generación cero, y así sucesivamente. Las generaciones que se consideran en nuestro análisis inicial son aquellas que dan origen a un zángano (generación 0). A continuación se indican las reglas de reproducción de las abejas.

Nota: En las imágenes que se usarán a lo largo de la unidad, las abejas reina siempre tienen una corona, mientras que los zánganos no.

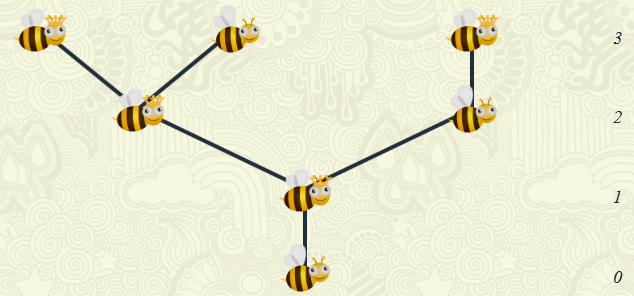
Nota lo siguiente:

• En la generación cero, se tiene el zángano a partir del cual se construye el árbol. Eso significa que hay una sola abeja en esta generación.


• En la primera generación, se tiene de quién provino el zángano. Por la regla, es una reina sola sin fecundar, por lo que también hay una sola abeja en esta generación.


• En la segunda generación, están las abejas de las que provino la reina anteriormente mencionada. Por la regla, viene de una reina fecundada por un zángano, entonces hay dos abejas en esta generación.


• En la tercera generación, se tiene por un lado de quién provino el zángano de la segunda generación y la reina de la segunda generación. El zángano, por la regla, tuvo que venir de una reina sola. La reina, por la regla, tuvo que venir de un zángano y una reina. Por lo mismo, hay tres abejas en esta generación.

A partir de estos datos, surgen las siguientes preguntas.

Seguro ya notaste que, si cuentas con el número y tipo de abejas que forman una generación, es posible calcular el número de abejas en la generación anterior (de la que vienen). Pero tal vez haya una forma de calcular el número de abejas en esta generación anterior considerando los números en generaciones posteriores sin importar cuántas abejas de qué tipo (reina o zángano) las componen.

Problema

En resumen, se busca obtener, para una generación $n$, el número de abejas en el árbol genealógico de éstas usando los números de generaciones siguientes.

Recursividad

Hablar de generaciones siguientes implica un concepto que se conoce como recursividad. Cuando algo es recursivo, quiere decir que su proceso (en nuestro ejemplo, el cálculo de abejas de una generación dada) se puede describir a partir de su propia definición. En este ejemplo, la definición de nuestro caso la dan las reglas mencionadas anteriormente. Y lo que buscamos es precisamente una fórmula para calcular el número de abejas de una generación determinada (es decir, el proceso mismo).

En el caso de las abejas, se trata de ver si hay alguna relación entre el número de abejas en la generación $n$ y el número de abejas en generaciones siguientes, por ejemplo, la generación siguiente ($n-1$) y la generación ($n-2$), que corresponde a dos generaciones adelante.

Adicionalmente, en procesos recursivos a menudo se encuentran patrones entre generaciones sucesivas. En el caso específico de las abejas, es interesante preguntarse si el cociente del números de abejas de generaciones sucesivas sigue algún comportamiento.

Problema

Se desea determinar si hay algún patrón en la razón del número de abejas de una generación $n$ al número de abejas en la generación siguiente ($n-1$). En particular, se busca si hay algún patrón en dicho cociente conforme se consideran valores más y más grandes de $n$.