En una población cuya distribución es conocida pero desconocemos algún parámetro, podemos estimar dicho parámetro a partir de una muestra representativa.

Un  estimador es un valor que puede calcularse a partir de los datos muestrales y que proporciona información sobre el valor del parámetro. Por ejemplo la media muestral es un estimador de la media poblacional, la proporción observada en la muestra es un estimador de la proporción en la población.

Una estimación es puntual cuando se obtiene un sólo valor para el parámetro. Los estimadores más probables en este caso son los estadísticos obtenidos en la muestra, aunque es necesario cuantificar el riesgo que se asume al considerarlos. Recordemos que l a distribución muestral indica la distribución de los valores que tomará el estimador al seleccionar distintas muestras de la población. Las dos medidas fundamentales de esta distribución son la media que indica el valor promedio del estimador y la desviación típica, también denominada error típico de estimación, que indica la desviación promedio que podemos esperar entre el estimador y el valor del parámetro.

Más útil es la estimación por intervalos en la que calculamos dos valores entre los que se encontrará el parámetro, con un nivel de confianza fijado de antemano.

• Llamamos Intervalo de confianza al intervalo que con un cierto nivel de confianza, contiene al parámetro que se está estimando.

• Nivel de confianza es la "probabilidad" de que el intervalo calculado contenga al verdadero valor del parámetro. Se indica por 1- a y habitualmente se da en porcentaje (1- a )100%. Hablamos de nivel de confianza y no de probabilidad ya que una vez extraída la muestra, el intervalo de confianza contendrá al verdadero valor del parámetro o no, lo que sabemos es que si repitiésemos el proceso con muchas muestras podríamos afirmar que el (1- a )% de los intervalos así construidos contendría al verdadero valor del parámetro.

La distribución muestral de medias es , por tanto si fijamos una probabilidad 1-α, sabemos que la es decir, el (1-α)% de las x está a una distancia de m inferior a

• Entonces para un nivel de confianza 1- α , µ pertenece al intervalo:  
  donde z_α/2 es el llamado valor crítico, valor tal que P(-z _α/2 £ z £ z _α/2 )=1- α , y x la media de la muestra.
• Si la desviación típica de la población es desconocida, lo que suele ocurrir en la práctica, la aproximaremos por la de la muestra siempre que n>100 

• Para 1-α = 0,95  α/2=0,025  z_α/2 =1,96 ya que en la tabla N(0,1) obtenemos p(z £ 1,96) = 0,975

Da a z, en la escena, el valor crítico que encuentres en la tabla N(0,1) para cada probabilidad.

Si deseamos estimar la proporción p con que una determinada característica se da en una población, a partir de la proporción p' observada en una muestra de tamaño n, sabemos que

• La distribución muestral de proporciones sigue una distribución normal con q=1-p
  Como la proporción p de la población es desconocida, se aproxima por la de la muestra siempre que n>100.

• Entonces para un nivel de confianza 1-α , p pertenece al intervalo:

• La proporción de piezas defectuosas en la muestra es 7/200=0,035

Calcula en la tabla N(0,1) los valores críticos y cambia en la escena el valor z

La amplitud del intervalo de confianza depende del valor de
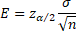
Con un nivel de confianza del (1-α)100% admitimos que la diferencia entre la estimación para la media a partir de la muestra y su valor real es menor que E, que llamaremos error máximo admisible.

• El tamaño de la muestra depende del nivel de confianza que se desee para los resultados y de la amplitud del intervalo de confianza, es decir del error máximo que se esté dispuesto a admitir. Fijados estos, 1-α y E, podemos calcular el tamaño mínimo de la muestra que emplearemos.

En el caso de estimar proporciones con lo que

• Para 1- α=0,90  α/2=0,05  z_α/2= 1,645

Fíjate cómo n varía también al cambiar el valor de z.

Calcula el tamaño que debería tener la muestra al nivel de confianza 95%