Podemos usar la Ecuación 3.3, pero como hemos visto, los resultados serían los mismos utilizando la Ecuación 3.4. $$\begin{aligned} m_{tan} &=\mathop {\lim }\limits_{x \to 2} \frac{f (x) −f (2)}{ x − 2} &\text{Aplicar la definición} \\ &= \mathop {\lim }\limits_{x \to 2} \frac{\frac{1}{x} − \frac{1}{2}}{x − 2} &\text{Sustituir} f (x) = \frac{1}{x} \,\,\,\text{y} \,\,\,f (2) = 1/2\\ &= \mathop {\lim }\limits_{x \to 2} \frac{\frac{1}{x} − \frac{1}{2}}{x − 2} \cdot \frac{2x}{2x} & \text{Multiplicar y dividir por 2x }\\ &= \mathop {\lim }\limits_{x \to 2} \frac{(2 − x)}{ (x − 2) (2x )} &\text{Simplificando} \\ &= \mathop {\lim }\limits_{x \to 2}\frac{−1}{2x} &\text{Calculando el límite} \\ &= \frac{−1}{4} \end{aligned}$$
Ahora sabemos que la pendiente de la recta tangente es $\frac{−1}{4}$. Para encontrar la ecuación de la recta tangente, también necesitamos un punto en la recta. Sabemos que $f (2) = \frac{1}{2}$, luego la recta tangente pasa por el punto $(2,\frac{1}{2})$. Usando la ecuación punto-pendiente de la recta, su ecuación es $y = −14x + 1$.
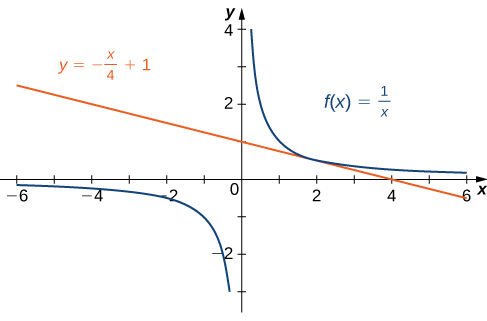
Las gráficas de $f (x) = 1/x$ e $y = \frac{−1}{4}x + 1$ se muestran en la Figura 3.7.
Esta figura consta de las gráficas de $f (x) = 1 / x$ y $y = -x / 4 + 1$. La parte de la gráfica $f (x) = 1 / x$ en el primer cuadrante parece tocar la gráfica de la otra función en $x = 2$.

Figura 3.7 La recta es tangente a $f (x)$ en $x = 2$.