En primer lugar calculamos la pendiente de la recta tangente, utilizando la expresión 3.3.
$$\begin{aligned} m_{tan} &= \mathop {\lim }\limits_{x \to 3} \frac{{f\left( x \right) - f\left( 3 \right)}}{{x - 3}} &{\text {Aplicar la definición}}\\ &= \mathop {\lim }\limits_{x \to 3} \frac{x^2-9}{x - 3} &{\text {Sustituir}} \,\,\,f (x) = x^2 \,\,\,\text{y} \,\,\,f (3) = 9 \\ &= \mathop {\lim }\limits_{x \to 3}\frac{ (x − 3) (x + 3)} {x − 3} &{\text {Factorizar el numerador para evaluar el límite}.}\\ &= \mathop {\lim }\limits_{x \to 3} (x + 3) = 6 \\ \end{aligned} $$Dado que la recta es tangente a la gráfica de $f (x)$ en $x = 3$, pasa por el punto $(3, f (3))$. Como $f (3) = 9$, la recta tangente pasará por el punto $(3,9)$.
Usando la ecuación punto-pendiente de la recta, teniendo en cuenta que la pendiente es $m = 6$ y el punto por el que pasa es $(3,9)$, obtenemos la recta $$y − 9 = 6 (x − 3)$$ Simplificando, tenemos $y = 6x − 9$.
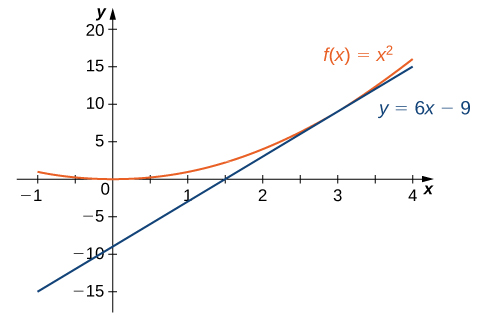
La gráfica de $f (x) = x^2$ y su recta tangente en 3 se muestran en la Figura 3.6.
Esta figura consta de las gráficas de $f (x) = x^2$ e $y = 6x - 9$. Las gráficas de estas funciones son tangentes en $x = 3$.

Figura 3.6 La recta tangente a $f (x)$ en $x = 3$.