Podemos usar la tabla de valores funcionales que se muestra en la Tabla 2.6. Observa que para valores de $x$ menores que 2, usamos $f (x) = x + 1$ y para valores de $x$ mayores que 2, usamos $f (x) = x^2−4$.
| $x$ | $f(x)=x+1$ | $x$ | $f(x)=x^2-4$ | |
| 1.9 | 2.9 | 2.1 | 0.41 | |
| 1.99 | 2.99 | 2.01 | 0.0401 | |
| 1.999 | 2.999 | 2.001 | 0.004001 | |
| 1.9999 | 2.9999 | 2.0001 | 0.00040001 | |
| 1.99999 | 2.99999 | 2.00001 | 0,0000400001 |
Tabla 2.6 Tabla de valores funcionales para $f(x) = \begin{cases} x+1 & \text{si $x < 2$} \\ x^2-4 & \text{si $x \ge 2$} \end{cases} $
Con base en esta tabla, podemos concluir que $$\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 3 \,\,\,\,\,\,\,\,\,\,\,\, \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 0$$
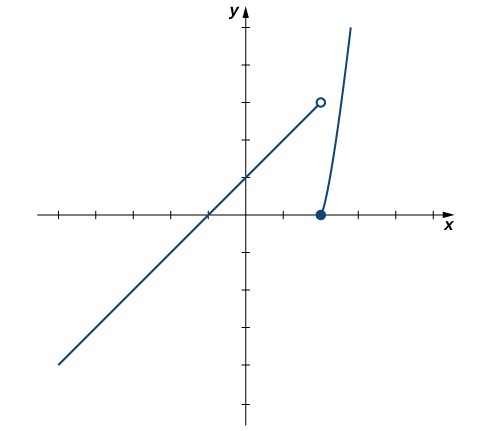
Por lo tanto, el límite (bilateral) de f (x) no existe en $x = 2$. La Figura 2.18 muestra una gráfica de $f (x)$ y refuerza nuestra conclusión sobre estos límites.

Figura 2.18 La gráfica de $f(x) = \begin{cases} x+1 & \text{si $x < 2$} \\ x^2-4 & \text{si $x \ge 2$} \end{cases} $ tiene un salto en $x=2$.