Solución

Como −1≤cos⁡x≤1 - 1 \le \cos x \le 1 para todo xx, tenemos −∣x∣≤xcos⁡x≤∣x∣ - \left| x \right| \le x\cos x \le \left| x \right|.

Teniendo en cuenta que

lim⁡x→0(−∣x∣)=0=lim⁡x→0∣x∣\mathop {\lim }\limits_{x \to 0} \left( { - \left| x \right|} \right) = 0 = \mathop {\lim }\limits_{x \to 0} \left| x \right|

por el teorema del Sandwich, obtenemos lim⁡x→0xcos⁡x=0\mathop {\lim }\limits_{x \to 0} x\cos x = 0.

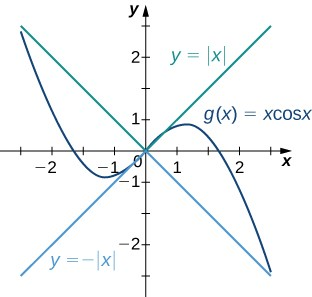
Las gráficas de f(x)=−∣x∣f (x) = - | x |, g(x)=xcosxg (x) = xcosx y h(x)=∣x∣h (x) = | x | se muestran en la Figura 2.28.

Figura 2.28 Las gráficas de f(x)f (x), g(x)g (x), y h(x)h (x) se muestran alrededor del punto x = 0.