Ejercicios - Capítulo 5

En los ejercicios 1 al 8, grafique el ángulo indicado, encuentre su correspondiente complementario, suplementario y cotrerminal. Además convierta grados en radianes o radianes en grados.

En los ejercicios 9 al 16. Demuestre que los puntos pertenecen al círculo unitario, halle las coordenadas faltantes o complete los triángulos rectángulos.

9. $\left(\cfrac{4}{5}\;\;,\;\;\cfrac{-3}{5}\right)\\[0.3cm]$
10. $\left(\cfrac{8}{25}\;\;,\;\;\cfrac{-24}{25}\right)\\[0.3cm]$

11. $P\left(\cfrac{-3}{5}\;\;,\;\;\;\;\right), \text{Cuadrante III}\\[0.3cm]$
12. $P\left(\;\;\;\;,\cfrac{-7}{25}\right), \text{Cuadrante IV}\\[0.3cm]$

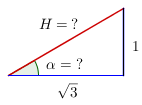
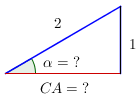
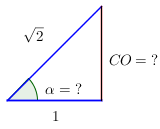
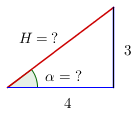
En los ejercicios 17 al 24. Utilice el Teorema de Pitágoras o las razones trigonométricas de los triángulos rectángulos para encontrar la solución.

17. $\hspace{0.1cm}$ Un carpintero tiene una tabla rectangular, con las dimensiones (en pulgadas) que se muesta en la siguiente figura, calcular el ángulo de inclinación $\alpha$ , el de elevación $\beta$ y las diagonales $CE \wedge ED$.

18. Si en el ejercicio anterior el corte inferir fuera a la mitad de la tabla, como se muesta en la figura, calcular el ángulo de inclinación $\alpha$ , el de elevación $\beta$, los demás ángulos y diagonales $CE \wedge ED$.

19. Una cometa queda atorada en los cables de un poste de energía. Si el hilo de 18 metros de la cometa forma un ángulo de $30^{\circ}$ con el suelo, estime a que altura esta la cometa y la distancia hasta su base.

20. Movimiento armónico: El desplazamiento desde el equilibrio de una masaoscilante unida a un resorte es $y\left(t\right)=4\cdot Cos\left(3\pi t\right)$, donde "$y$" se mide en pulgadas y "$y$" en segundos. Calcule el desplazamiento en los tiempos indicados en la tabla.

21. Circuito eléctrico: Después de que se cierra el interruptor en el circuito mostrado, la corriente t segundos más tarde es $I(t)=0.8 e^{-3t}\cdot Sen \left(10t\right)$. Calcule la corriente en los tiempos: $\\[0.1cm]\text{a.}\; t =0.1 s\\[0.1cm]\text{ b.} t = 0.5 s$

22. Desde un cierto punto del terreno se mira a lo alto de una montaña y la visual forma un ángulo de $60^{\circ}$ con el suelo. Al alejarse 200 m de la montaña, la visual forma $30^{\circ}$ con el suelo. Halla la altura "$h$" de la montaña y la distancia "$s$", luego de alejarse los 200 m.
23. El piloto de un avión que vuela a 2000 m de altura, divisa la ciudad de destino con un ángulo de depresión de $15^{\circ}$. A qué distancia está esa ciudad?.
24. Calcular la altura de una antena de radio si su sombra mide 100 m cuando los rayos del Sol forman un ángulo de $23^{\circ}$ con la horizontal

En los ejercicios 25 al 32. Utilice la ley del seno o ley del coseno para encontrar la solución.

25. En el paralelogramo ABCD la longitud del lado $\overline{AB}$ es 14 metros, la de $\overline{AD}$ es 8 metros y el ángulo $m\left(\measuredangle DAB\right)$ es $80^{\circ}$. Halle la longitud de las diagonales del paralelogramo.
26. Un rombo tiene un lado que mide 8.5 centímetros y un ángulo de base de $75^{\circ}$. Halle la longitud de las diagonales.
27. Dos “boy scouts” quieren estimar la distancia entre su campamento situado en el punto $A$ y otro campamento en $C$ en el lado opuesto de un lago, como se muestra en la figura. Ellos marcan una línea desde su campamento hasta un punto $B$ a 50 metros. Si el $\measuredangle BAC$ mide $88^{\circ}$ y el $\measuredangleABC$ mide $75^{\circ}$. ¿Cuál es la distancia aproximada entre los dos campamentos?

28. Alberto, Bernardo y Carlos están considerando la compra de un equipo de comunicaciones con un alcance de 200 metros. Bernardo vive al otro lado de una carrilera que pasa entre su casa y las de Alberto y Carlos. Hicieron el dibujo y tomaron las medidas que muestran la figura. ¿Puede cada uno de los muchachos comunicarse con los otros dos con el equipo?

29. Un grupo de matemáticos se va a una cacería "de observación" de animales que se alimentan de carroña. Una parte de las indicaciones dice que hay una presa enterrada que se puede encontrar en la forma siguiente: "Un grupo debe hacer un circulo de guijarros tomando como centro el tronco $A$ y radio de 45 metros. Los otros participantes deben caminar hacia el oeste del tronco 75 metros hasta llegar a un punto $B$, donde deben cambiar su rumbo hacia N$44^{\circ}$E. La presa estará en la intersección $C$ de este camino con el circulo de guijarros". Juanita Martínez dice que esta parte de la cacería es una chanza. ¿Está en lo cierto?
30. Un camionero parte de la bodega $A$ y viaja 40 kilómetros con rumbo N$10^{\circ}$E hasta el punto $B$, donde se vara por falla mecánica. Avisa por radio a su central $C$, el cual se encuentra 20 kilómetros al oeste de la bodega. ¿A qué distancia de su central está detenido el camión?
31. Un velero sale de una playa en el muelle $A$ y navega $4\dfrac {1}{2}$ millas náuticas hacia el este. Luego cambia de rumbo y navega $2\dfrac {3}{4}$ de millas en dirección N$45^{\circ}$E.
$\text{a.\;¿Cuál es la distancia del velero al muelle?}\\[0.1cm] \text{b.\;¿Cuál es la distancia del velero al muelle?}$
32. Un poste vertical de 40 pies de altura se encuentra sobre una ladera que forma un ángulo de $17^{\circ}$ con la horizontal, como se muestra en la figura. Calcule la longitud mínima de cable que llegará de lo alto del poste a un punto situado a 72 pies colina abajo desde la base del mismo.

En los ejercicios 33 al 40. Realice la demostración de las identidades trigonométricas (se presenta una posible solución).

33. $Sen^2{\theta}\left(1+Cot^2{\theta}\right)\equiv 1$
34. $Tan{\theta}+Cot{\theta}\equiv Sec\;{\theta}\cdot Csc\;{\theta}$
35. $Tan\;{\theta}+\cfrac{Cos{\theta}}{1+Sen{\theta}}\equiv Sec\;{\theta}$
36. $\cfrac{1+Sen\;{\alpha}}{1-Sen\;{\alpha}}-\cfrac{1-Sen\;{\alpha}}{1+Sen\;{\alpha}}\equiv 4Tan\;\alpha\cdot Sec\;{\alpha}$

37. $Sen\;{\theta}\left(Csc\;\theta-Sen{\theta}\right)\equiv Cos^2\;{\theta}$
38. $\left(1-Cos^2\;{\theta}\right)\left(1+Cot^2{\theta}\right)\equiv 1$
39. $Cos\;{\beta}\left(Tan\;\beta+Cot{\beta}\right)\equiv Csc\;{\beta}$
40. $Sec{\theta}-Tan{\theta}\equiv \cfrac{1-Sen\;{\theta}}{Cos\;{\theta}}$

En los ejercicios 41 al 52. Resuelva las ecuaciones trigonométricas y exprese la solución en grados o radianes.

41. $\hspace{0.1cm}4Sen\;{\theta}\cdot Cos\;\theta+6Sen{\theta}+2Cos{\theta}+3= 0$
42. $\hspace{0.1cm}Cos\;x +1=2Sen^2\;x$
43. $\hspace{0.1cm}Sen\;2x\left(Csc\;2x-2\right)=0$
44. $\hspace{0.1cm}Sen\left(\theta+\cfrac{\pi}{4}\right)=\cfrac{1}{2}$

49. $\hspace{0.1cm}2Sen\;x\cdot Cos^2x=-\cfrac{\sqrt{3}}{2}Cos\;x$
50. $\hspace{0.1cm}1+Tan\;\alpha=Sec\;\alpha$
51. $\hspace{0.1cm}2Cos^2\theta-3Cos\;\theta$
52. $\hspace{0.1cm}Sen\;2x+Sen\;x=0$

45. $\hspace{0.1cm}\sqrt{3}+2Sen\;beta=0$
46. $\hspace{0.1cm}Sen\left(2-\cfrac{\pi}{3}\right)=\cfrac{1}{2}$
47. $\hspace{0.1cm}Sec\;x\cdot Sen^2x=Tan\;x$
48. $\hspace{0.1cm}1+Cot\;\theta=Csc\;\theta$