Preguntas - Capítulo VI

1. Cuál es el modelo matemático para el principio del impulso y el momento lineal?

2. Cómo se interpreta el modelo matemático para el principio del impulso y el momento lineal?

3. Cuál es el modelo matemático para el principio de conservación del momentum lineal?

4. Qué nos indica el modelo matemático para el principio de conservación del momentum lineal?

5. Cómo se entiende el fenómeno del impacto entre dos cuerpos en física?

6. Qué es la línea de impacto?

7. Qué es el plano de contacto?

8. Cuándo un impacto es central?

9. Cuándo un impacto es oblicuo?

10. Qué es el Coeficiente de restitución $\color{#0000FF} e$?

11. Cuál es el modelo matemático para el Coeficiente de restitución $\color{#0000FF} e$.

12. Qué es un impacto perfectamente elástico?

13. Qué es un impacto perfectamente inelástico?

14. En un impacto entre dos cuerpos que consecuencia trae un Coeficiente de restitución $\color{#0000FF} e=0$?

15. Qué es Momento angular    $\color{#0000FF} \overrightarrow {H_0}$?

16. Cuál es el modelo matemático para el momento angular   $\color{#0000FF} \overrightarrow {H_0}$?

17. Cuál es el modelo matemático que relaciona el Momento de Fuerza $\color{#0000FF} \overrightarrow {M_0}$ con el Momento angular $\color{#0000FF} \overrightarrow {H_0}$?

18. Qué significado tiene el modelo matemático que relaciona el Momento de Fuerza $\color{#0000FF} \overrightarrow {M_0}$ con el Momento angular $\color{#0000FF} \overrightarrow {H_0}$ y que nombre recibe?

19. En la expresión $\color{#0000FF} \dot {\overrightarrow {H_0}} = {\color{Red}\bcancel {{\color{blue}\dfrac {d \overrightarrow {r}}{dt} \times m \overrightarrow {v}}}} + \overrightarrow {r} \times m \dot {\overrightarrow {v}}$?, el termino cancelado es igual a cero $\color{#0000FF} 0$, por qué razón?

20. Cómo es la dirección y sentido del vector momento angular $\color{#0000FF} \overrightarrow {H_0}$ respecto del vector de posición $\color{#0000FF} \overrightarrow {r}$ y el vector velocidad $\color{#0000FF} \overrightarrow {v}$

Ejercicios - Capítulo VI

1. Al bloque de hielo de $\hspace{0.1cm} \color{#0000FF} 200 {Kg} \ $ estando en reposo sobre la superficie lisa horizontal se le aplica durante $\hspace{0.1cm} \color{#0000FF} 10 \ {s} \ $ una fuerza de $\hspace{0.1cm} \color{#0000FF} 400 \ {N} \ $ a un ángulo de $\hspace{0.1cm} \color{#0000FF} 30° \ $ en las condiciones que muestra la figura. Determine la velocidad del bloque de hielo al final de los $\hspace{0.1cm} \color{#0000FF} 10 \ {s} \ $.

2. Sobre la caja de $\hspace{0.1cm} \color{#0000FF} 60 \ {Lb} \ $ actua una fuerza de $\hspace{0.1cm} \color{#0000FF} F=50 \ {Lb} \ $ estando en reposo como muestra la figura. Determine la velocidad de la caja $\hspace{0.1cm} \color{#0000FF} 4 \ {s} \ $ después. El coeficiente de rozamiento cinético entre la caja y el plano inclinado es $\hspace{0.1cm} \color{#0000FF} \mu_k=0.2 \ $.

3. El bloque $\hspace{0.1cm} \color{#0000FF} A \ $ es de $\hspace{0.1cm} \color{#0000FF} 10 \ {Kg} \ $, el bloque $\hspace{0.1cm} \color{#0000FF} B \ $ es de $\hspace{0.1cm} \color{#0000FF} 5 \ {Kg} \ $. El sistema se libera desde el reposo. Determine la velocidad de cada bloque y la tensión en la cuerda $\hspace{0.1cm} \color{#0000FF} 6 \ {s} \ $ después de liberarse. El coeficiente de rozamiento cinético entre el bloque $\hspace{0.1cm} \color{#0000FF} A \ $ y la superficie es $\hspace{0.1cm} \color{#0000FF} \mu_k=0.1 \ $.

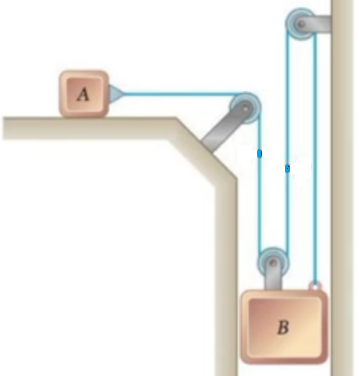
4. La bola de beisbol de $\hspace{0.1cm} \color{#0000FF} 0.4 \ Kg \ $ lleva una rapidez horizontal de $\hspace{0.1cm} \color{#0000FF} 20 \ \dfrac {m}{s} \ $ y es golpeada por el bate cambiándole su trayectoria a $\hspace{0.1cm} \color{#0000FF} 30° \ $ arriba de la horizontal como muestra la figura, alcanzando una altura máxima de $\hspace{0.1cm} \color{#0000FF} 50 \ m \ $ respecto del bate. Determine el impulso del bate sobre la bola.

5. El bloque $\hspace{0.1cm} \color{#0000FF} A \ $ es de $\hspace{0.1cm} \color{#0000FF} 10 \ {Lb} \ $, el bloque $\hspace{0.1cm} \color{#0000FF} B \ $ es de $\hspace{0.1cm} \color{#0000FF} 5 \ {Lb} \ $. El sistema se libera desde el reposo. Determine el coeficiente de rozamiento cinético entre el bloque $\hspace{0.1cm} \color{#0000FF} A \ $ y la superficie horizontal, la tensión $\hspace{0.1cm} \color{#0000FF} T \ $ y la velocidad del bloque $\hspace{0.1cm} \color{#0000FF} A \ $ pasados $\hspace{0.1cm} \color{#0000FF} 4 \ s \ $ de liberarse el sistema; si se sabe que la velocidad del bloque $\hspace{0.1cm} \color{#0000FF} B \ $ es de $ \hspace{0.1cm} \color{#0000FF} 2 \ \dfrac {ft}{s} \ $.

6. El vagón $\hspace{0.1cm} \color{#0000FF} A \ $ de $\hspace{0.1cm} \color{#0000FF} 12000 \ {Kg} \ $ se desplaza por la vía a $ \hspace{0.1cm} \color{#0000FF} 4 \ \dfrac {m}{s} \ $. El vagón $\hspace{0.1cm} \color{#0000FF} B \ $ de $\hspace{0.1cm} \color{#0000FF} 10000 \ {Kg} \ $ se desplaza por la vía a $ \hspace{0.1cm} \color{#0000FF} 2 \ \dfrac {m}{s} \ $ como se muestra en la figura. Si los vagones en estas condiciones impactan y se acoplan, determine la velocidad común de los vagones una vez se han acoplado y determine la magnitud de la fuerza promedio en el acoplamiento si este dura $\hspace{0.1cm} \color{#0000FF} 0.5 \ s \ $.

7. Una bala de $\hspace{0.1cm} \color{#0000FF} 0.02 \ Kg \ $ es disparada por la pistola de $\hspace{0.1cm} \color{#0000FF} 1.2 \ Kg \ $ con una velocidad de $\hspace{0.1cm} \color{#0000FF} \overrightarrow 550 \dfrac {m}{s} \rightarrow \ $. Determine la velocidad del retroceso de la pistola.

8. Un martillo de $\hspace{0.1cm} \color{#0000FF} 40 \ Lb \ $ se desplaza a $\hspace{0.1cm} \color{#0000FF} 35 \dfrac {ft}{s} \downarrow \ $ golpeando la cabeza del clavo. si el martillo se detiene $\hspace{0.1cm} \color{#0000FF} 0.0015 \ s \ $ luego. Determine el impulso y la fuerza promedio sobre el clavo.

9. La bola de golf de $\hspace{0.1cm} \color{#0000FF} 0.1 \ Kg \ $ despega del tee con una rapidez de $\hspace{0.1cm} \color{#0000FF} 10 \dfrac {m}{s} \ $ por la acción de una fuerza de $\hspace{0.1cm} \color{#0000FF} 1000 \ N \ $. Determine el valor del impulso y el tiempo que duro el impacto.

10. Un proyectil de $\hspace{0.1cm} \color{#0000FF} 4 \ {Lb} \ $ teledirigido, viaja horizontalmente a $\hspace{0.1cm} \color{#0000FF} 50 \ \dfrac {ft}{s} \ $ y de pronto estalla en tres fragmentos que salen disparados en un mismo plano vertical. Un fragmento de $\hspace{0.1cm} \color{#0000FF} 1.5 \ {Lb} \ $ sale disparado a un ángulo de $\hspace{0.1cm} \color{#0000FF} 30° \ $ arriba de la horizontal; otro fragmento de $\hspace{0.1cm} \color{#0000FF} 0.5 \ {Lb} \ $ sale disparado a $\hspace{0.1cm} \color{#0000FF} 60° \ $ abajo de la horizontal y el último fracmento sale disparado a $\hspace{0.1cm} \color{#0000FF} 120° \ $ arriba de la Horizontal a una rapidez de $\hspace{0.1cm} \color{#0000FF} 20 \ \dfrac {ft}{s} \ $. Determine la rapidez de los otros dos fragmentos.

11. El proyectil de $\hspace{0.1cm} \color{#0000FF} 12 \ {Lb} \ $ es disparado desde el nivel del suelo (despreciando el tamaño del cañón) a $\hspace{0.1cm} \color{#0000FF} 100 \dfrac {ft}{s} \ $ a un ángulo $\hspace{0.1cm} \color{#0000FF} \theta_0 = 60° \ $. Cuando el proyectil está en el punto mas alto explota y queda en dos fragmentos de $\hspace{0.1cm} \color{#0000FF} 6 \ {Lb} \ $ cada uno. Uno de los fragmentos sale disparado en dirección vertical hacia arriba y luego cuando caen quedan separados $\hspace{0.1cm} \color{#0000FF} 120 \ {ft} \ $. Todo el movimiento sucede en el mismo plano vertical a la tierra. Determine la velocidad de cada fragmento justo un instante luego de la explosión.

12. El proyectil de $\hspace{0.1cm} \color{#0000FF} 20 \ {Kg} \ $ es disparado desde el nivel del suelo (despreciando el tamaño del cañón) a $\hspace{0.1cm} \color{#0000FF} 50 \dfrac {m}{s} \ $ a un ángulo $\hspace{0.1cm} \color{#0000FF} \theta_0 = 60° \ $. Cuando el proyectil está en el punto mas alto explota y queda en dos fragmentos de $\hspace{0.1cm} \color{#0000FF} 10 \ {Kg} \ $ cada uno. Uno de los fragmentos sale disparado en dirección vertical hacia arriba con una rapidez de $\hspace{0.1cm} \color{#0000FF} 30 \dfrac {m}{s} \ $. Si todo el evento sucede en el mismo plano vertical a la tierra; determine la velocidad del otro fragmento y la separación entre los dos fragmentos al caer al suelo.

13. El sistema se conoce como péndulo balístico, sirve especialmente para conocer la velocidad inicial del proyectil. El proyectil de $\hspace{0.1cm} \color{#0000FF} 0.01 \ {Kg} \ $ es disparado hacia el bloque de madera de $\hspace{0.1cm} \color{#0000FF} 2 \ {Kg} \ $ suspendido de cuerdas ligeras. El proyectil es detenido por el bloque el cual se balance desde el reposo hasta alcanzar la altura máxima de $\hspace{0.1cm} \color{#0000FF} 0.05 \ {m} \ $. Determine la velocidad con la que el proyectil impacta el bloque.

14. La esfera $\hspace{0.1cm} \color{#0000FF} A \ $ de $\hspace{0.1cm} \color{#0000FF} 3.5 \ {Lb} \ $ se desliza por la pista lisa hacia la derecha a $\hspace{0.1cm} \color{#0000FF} 10 \dfrac {ft}{s} \ $ choca contra un resorte unido a la esfera $\hspace{0.1cm} \color{#0000FF} B \ $ de $\hspace{0.1cm} \color{#0000FF} 5.5 \ {Lb} \ $ que se desliza por la pista lisa hacia la izquierda a $\hspace{0.1cm} \color{#0000FF} 6 \dfrac {ft}{s} \ $ . El resorte tiene una constante elastica de $\hspace{0.1cm} \color{#0000FF} 40 \dfrac {Lb}{ft} \ $. Determine la velocidad de la esfera $\hspace{0.1cm} \color{#0000FF} A \ $ y la compresión del resorte para cuando la esfera $\hspace{0.1cm} \color{#0000FF} B \ $ queda en reposo luego de la colisión.

15. La esfera $\hspace{0.1cm} \color{#0000FF} A \ $ de $\hspace{0.1cm} \color{#0000FF} 1 \ Kg \ $ impacta con la esfera $\hspace{0.1cm} \color{#0000FF} B \ $ de $\hspace{0.1cm} \color{#0000FF} 2 \ Kg \ $ con las velocidades iniciales $\hspace{0.1cm} \color{#0000FF} v_{A_i} = 6 \dfrac {m}{s} \ $ y $\hspace{0.1cm} \color{#0000FF} v_{B_i} = 2 \dfrac {m}{s} \ $ en las direcciones que muestra la figura. Determine las componentes de la velocidad final de cada esfera a lo largo de la línea de impacto y la línea que representa el plano de contacto, si el coeficiente de restitución para las esferas es de $\hspace{0.1cm} \color{#0000FF} 0.75\ $.

16. La esfera $\hspace{0.1cm} \color{#0000FF} A \ $ de $\hspace{0.1cm} \color{#0000FF} 1 \ Lb \ $ impacta con la esfera $\hspace{0.1cm} \color{#0000FF} B \ $ de $\hspace{0.1cm} \color{#0000FF} 2 \ Lb \ $ con las velocidades iniciales $\hspace{0.1cm} \color{#0000FF} v_{A_i} = 20 \dfrac {ft}{s} \ $ y $\hspace{0.1cm} \color{#0000FF} v_{B_i} = 0 \dfrac {ft}{s} \ $ como se muestra en la figura. Determine el coeficiente de restitución para las esferas, si se sabe que las velocidades finales son $\hspace{0.1cm} \color{#0000FF} v_{A_f} = 12 \dfrac {ft}{s} \ $ y $\hspace{0.1cm} \color{#0000FF} v_{B_i} = 16 \dfrac {ft}{s} \ $, ambas en la misma dirección a la derecha.

17. El patinador de $\hspace{0.1cm} \color{#0000FF} 180 \ Lb \ $ viaja hacia abajo por la rampa circular lisa. Cuando pasa por el punto $\hspace{0.1cm} \color{#0000FF} A \ $ forma un ángulo $\hspace{0.1cm} \color{#0000FF} \theta = 30° \ $ lleva una rapidez de $\hspace{0.1cm} \color{#0000FF} 18 \dfrac {ft}{s} \ $. Determine el momento angular respecto del punto $\hspace{0.1cm} \color{#0000FF} 0 \ $ y la aceleración tangencial en ese instante. El radio de curvatura es de $\hspace{0.1cm} \color{#0000FF} 12 \ ft \ $.

18. La varilla de masa despreciable de $\hspace{0.1cm} \color{#0000FF} 4 \ ft \ $ de longitud tiene en cada extremo una esfera de $\hspace{0.1cm} \color{#0000FF} 2 \ Lb \ $. Determine el momento angular para cuando el sistema gira alrededor de su centro en $\hspace{0.1cm} \color{#0000FF} 0 \ $ con velocidad angular constante de $\hspace{0.1cm} \color{#0000FF} 10 \dfrac {rad}{s} \ $. Determine la rapidez de cada esfera si en el sistema las masas al girar se desplazan a la mitad de la medida del radio cada una.

19. La varilla de masa despreciable de $\hspace{0.1cm} \color{#0000FF} 4 \ ft \ $ de longitud tiene en cada extremo una esfera de $\hspace{0.1cm} \color{#0000FF} 2 \ Lb \ $. Determine el momento ángular para cuando el sistema gira al rededor de un eje imaginario que pasa perpendicular a la varilla y atraviesa el centro de una de las esferas. Determine el momento angular para cuando el sistema gira alrededor de un eje imaginario que pasa paralelo al eje de la varilla pasando por el centro de las esferas si se sabe que el sistema gira con velocidad angular constante de $\hspace{0.1cm} \color{#0000FF} 10 \dfrac {rad}{s} \ $.

20. Una esfera de $\hspace{0.1cm} \color{#0000FF} 2 \ Kg \ $comienza a girar desde el reposo en una pista circular de radio $\hspace{0.1cm} \color{#0000FF} 0.5 \ m \ $ con aceleración tangencial de $\hspace{0.1cm} \color{#0000FF} 2 \dfrac {m}{s^2} \ $. Determine el momento angular respecto del centro de la circunferencia, el momento de las fuerzas que actúan sobre la esfera respecto del centro de la circunferencia y demuestre que la derivada respecto del tiempo del momento angular es igual al momento producido por las fuerzas que actúan sobre la esfera.